伺服控制系统震动的检测和抑制
龚文全,柯炜
(南海信息技术学校,广东 佛山 528000)
0 引言
在电机伺服控制系统中,电动机和负载加工装置之间,常使用联轴器、齿轮组等传动器件连接,一方面可以传递力矩,一方面可以实现对负载加工的精准控制[1]。由于实际材料的限制,常见的传动器件具有弹性,在传递力矩的工作过程中会发生弹性形变,弹性形变一般会使力矩传递延迟,影响生产加工的控制精度,严重时会激发系统的谐振点,使整个电机控制系统出现剧烈的震荡,也就是机械谐振[2],影响加工控制精度。
国内外学者在电机控制系统谐振抑制方面做了大量研究。文献[ 3]对速度环进行PI参数整定,得到较为准确的控制参数,实现了电机转速波动抑制。文献[ 4]对电机控制系统通过多频率扫频法,在系统离线的状态先,输入扫频信号,检测出电机控制系统的谐振点,然后设计二阶陷波滤波器,实现了转速振动抑制。文献[ 5]对转速误差信号做快速傅里叶分析,得到谐振频率,然后使用陷波器实现了机械谐振的在线检测和抑制。文献[ 6]对FFT进行改进,采用滑动DFT算法进行频率辨识,减小了计算量。
为了解决使用陷波滤波器带来的相位滞后影响,文献[ 7]提出优先考虑零相位滤波器ZPNF(Zero-phase notch filter),利用零相位陷波器的相位特征,减小电机控制系统的整体相位滞后,实验结果表明,机械手的控制速度跟随行和定位精确度明显提高。文献[ 8]对传统的零相位陷波器进行改进,然后将陷波器接入位置控制回路,滤除输入的位置控制信号中的谐振频率信号,实现了机械臂的谐振抑制。文献[ 9]把ZPNF和ZPETC(zero phase error tracking controller)方案综合考虑,在实现系统谐振抑制的同时,保证了系统的相位,仿真结果表明了该方案的有效性。文献[ 10]对陷波器的结构进行改进,提出一种相位补偿策略。但是上述研究多是关注位置环回路,但在工业生产中最常见的控制形式是速度环控制,却很少有详细的研究。
本文首先建立起电机控制系统的谐振模型,利用全局渐近频率估计算法[11-13],对转速误差信号进行在线分析,然后基于传统二阶陷波滤波器,提出一种相位滞后更小的改进型陷波滤波器。最后通过simulink,分别进行传统陷波器和改进型陷波器的谐振抑制效果对比,并且对实验结果进行分析分析,仿真结果验证了本文所提策略的有效性。
1 系统建模及谐振分析
1.1 机械谐振机理分析
在交流电机伺服系统中,当传动器件刚度不足时,常将柔性伺服系统简化为二质量模型来分析,如图1所示。
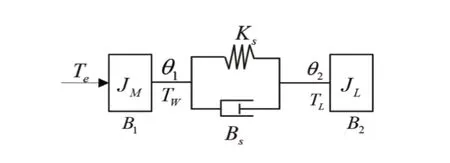
图1 柔性伺服系统二质量模型
电机电磁转矩和负载转速之间的微分方程组如(1)所示:

其中:
Ks:刚度系数 Bs:阻尼系数
Te:电机电磁转矩 Tw:弹性连接转矩
Jm:电机转动惯量 B1:电机转轴阻尼
JL:负载转动惯量 B2:负载阻尼系数
TL:负载转矩
忽略阻尼系数,电磁转矩和电机转速可得到如式(2)传递函数为
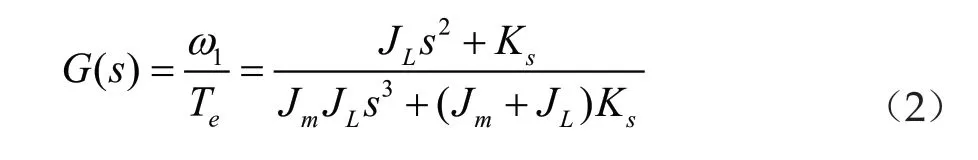
式(3)的极点被称为谐振频率点 NTF为

根据自动控制原理可知,极点的存在会影响系统的稳定性,如果有对应频率信号输入,系统就会出现强烈的响应,破坏系统稳定性,在电机控制系统中被称为机械谐振。
1.2 谐振频率变化的原因
对于电机、传动器件和负载加工台等环节确定的电机控制系统,其机械谐振频率理论上也是唯一确定的,但是在实际的制造加工中,由于松动磨损、传动器件变形等因素,将会使谐振频率发生偏移,图2是模拟更换不同传动刚度的传动器件时,二质量谐振系统的谐振点变化的伯德图。

图2 不同的传动刚度系数
从图2可以看出,当更换传动器件时,谐振频率很容易出现变化,准确获得系统谐振频率,是实现谐振抑制的前提,因此,需要对谐振频率进行在线检测,从而设计陷波滤波器进行准确滤波,以获得良好的谐振抑制效果。
2 ANF频率估计算法
本文利用M.Mojiri提出的全局渐近频率估计算法,来提取谐振频率。
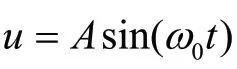

图3 ANF频率估计基本框图
当输入信号为
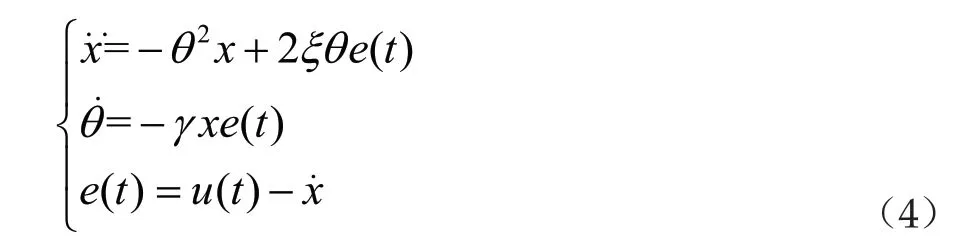
e(t)是输入信号u(t)与提取出的状态分量之间的误差值。
可得到唯一解为

此时,θ就是检测出的输入信号基波角频率。
3 陷波滤波器的分析和改进
3.1 陷波器工作原理
陷波滤波器带阻滤波器的一种,作用是滤除中心频率对应的信号,通过其余信号,理想陷波滤波器的幅频特性如图4。
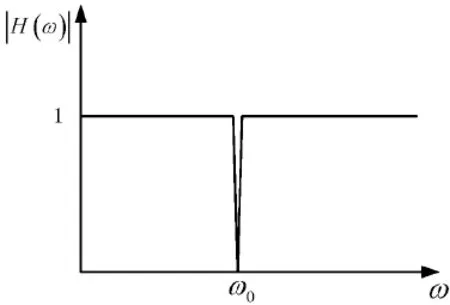
图4 理想陷波滤波器幅频特性
理想陷波器形式为
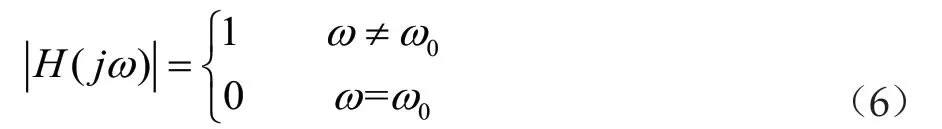
理想陷波器难以实现,实际中常采用二阶陷波滤波器结构为
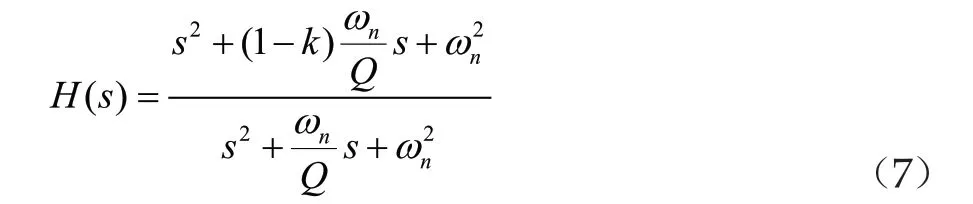
其中k为陷波深度参数,Q为陷波宽度参数。
柔性电机伺服系统具有谐振点,如果有对应频率的信号输入,则会激发谐振点,导致谐振现象,因此将陷波滤波器串入速度回路,滤除电流中的谐振频率激励信号,抑制电磁转矩震荡,从而实现电机转速谐振抑制,对于双闭环柔性电机伺服谐振抑制系统,其控制框图如图5。

图5 基于陷波滤波器的谐振抑制框图
3.2 陷波器的相位影响
当把陷波器加入到伺服系统中,如果谐振频率检测精准,则可以利用陷波器实现谐振抑制,但同时也会把陷波器本身的相位滞后引入到系统中,导致系统整体相位滞后更加严重,有自动控制原理的相位稳定条件可知,系统相位裕度不足时,可能会失去稳定。对于式(7),令s=jω

写出其相角特性表达式为

则相角损失为
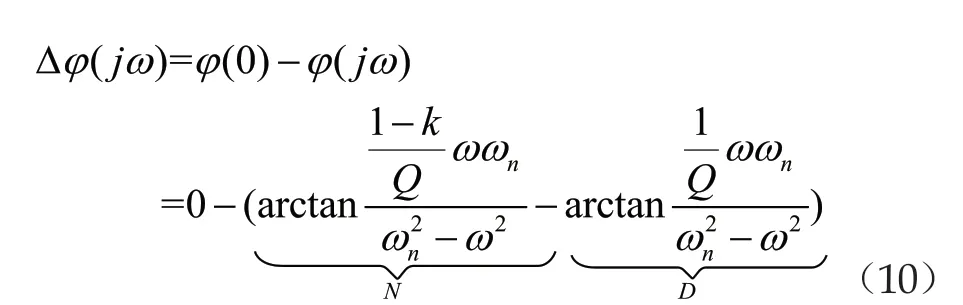
3.3 改进型陷波滤波器
为了增大φ(j)ω,可以减小D部分,或则增大N部分,但N中包含系统零点,改变N容易导致陷波器的零点和谐振系统的不稳定极点无法对消,谐振抑制失败或者造成新的不稳定,因此,在D中引入参数a,此时式(7)可以写为

当a=1时,陷波器结构无改变,相位保持原特性。当a>1时,φ(j)ω增大,相角损失Δφ(j)ω变小。
当a>1时,陷波器结构被改变,会改变陷波器的陷波深度,影响实际的谐振抑制效果,写出式(11)幅值表达式为

因此,当a=1时,常规陷波器的最大衰减倍数为

当a>1时,对应的陷波深度将减小。
取a=1.5,画出改进前后陷波滤波器的相位特性图,如图6所示。

图6 陷波器幅频特性对比

二者最大陷波深度约变化了2dB,但是改进型陷波器相角损失明显减小,所以,改进型陷波器以较小的陷波深度损失,获得了较大的相位补偿,实现了系统相位裕度增加,提高了系统的稳定性。
4 仿真验证和分析
4.1 基于ANF的谐振频率检测
在Simulink中搭建柔性电机伺服系统仿真模型,相关仿真参数如表1所示,验证ANF谐振频率估计效果:
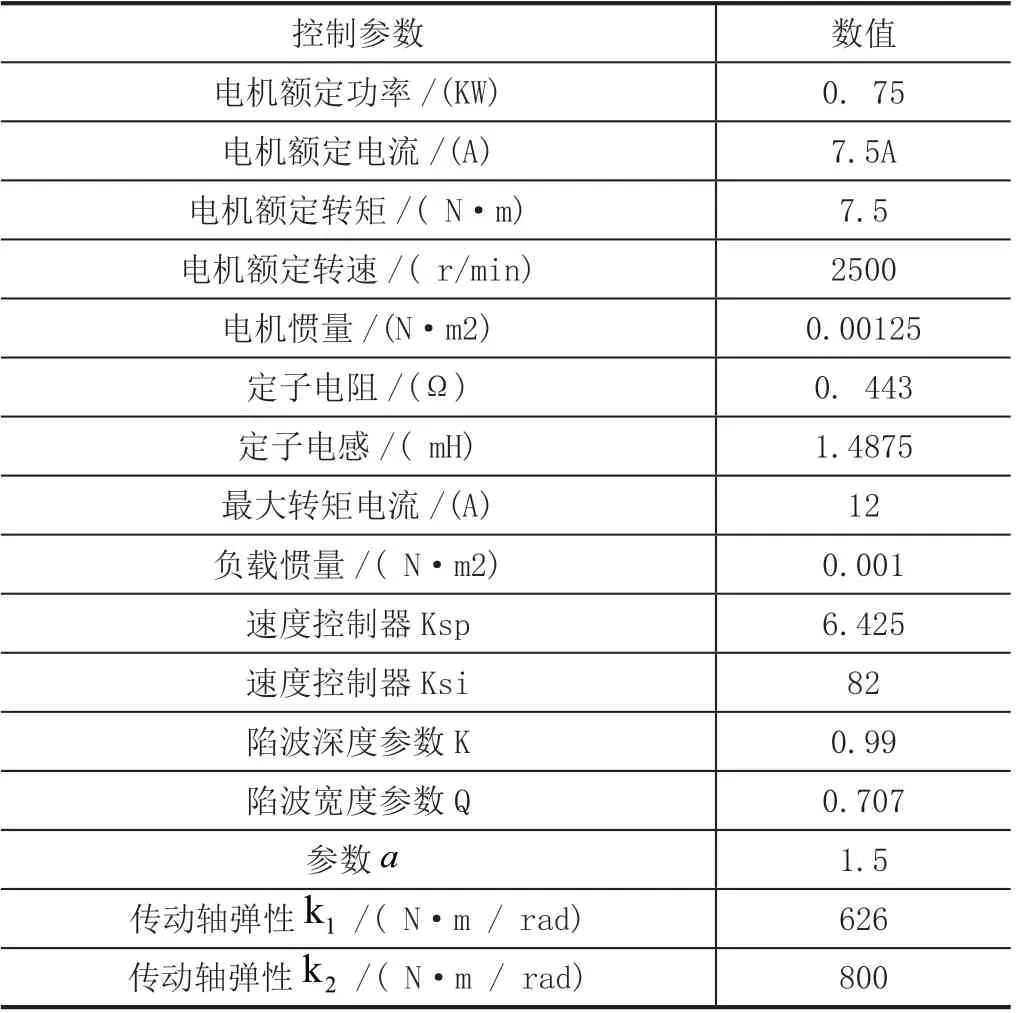
表1 表贴式永磁同步电机仿真参数
当伺服系统发生机械谐振时,以电机转速误差为输入信号,使用ANF频率估计算法对谐振频率进行检测,检测结果如图7所示:

图7 两种刚度频率估计结果

4.2 基于改进型陷波器的谐振抑制
为通过ANF获得系统的谐振频率后,系统速度给定为130rad/s,使电机伺服系统发生机械谐振,并接入陷波滤波器。
(1)对比无陷波处理的电机转速,和使用常规陷波滤波器的电机转速,其仿真结果如图8所示:
从图8可以看出,当伺服系统发生机械谐振,加入常规陷波滤波器,系统最终稳定在给定值,震荡得被抑制,但是动态响应阶段存在滞后。
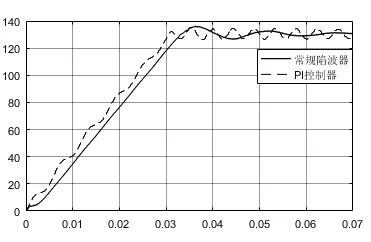
图8 常规陷波器抑制效果
(2)比较加入改进型陷波器后的转速响应,其仿真结果如图9所示:

图9 改进前后陷波器抑制效果对比
从图9可以看出,加入陷波器后,伺服系统的转速震动均能很好的被抑制,但是与常规陷波器相比,加入改进型陷波器的系统,动态性能得到了改善,响应速度明显提高,而且稳定速度明显加快,其具体动态指标如表2所示:

表2 两种陷波策略动态性能
通过表2可以看出,由于改进型陷波滤波器的相位损失更小,对系统产生的滞后更小,电机转速上升时间加快,峰值变小,超调量减小,调节时间更短,速度稳定更快。与常规陷波的抑制效果相比,使用改进型陷波器,系统动态性能得到了改善。
5 结语
本文以柔性电机伺服控制系统中存在的机械谐振问题为研究对象,通过ANF算法对谐振频率进行检测,针对常规陷波滤波器所造成的系统相位损失,提出一种改进型陷波滤波器,在 Matlab 环境中进行谐振抑制仿真分析,所得结论如下:
(1)柔性伺服系统的谐振频率点受到电机转动惯量、传动轴刚度系数和负载惯量的影响而发生变化。
(2)将ANF频率估计算法应用到谐振检测中,仿真结果表明,频率检测值准确可用,为伺服系统机械谐振检测提供了新思路。
(3)对常规陷波器相位特性分析之后,提出一种改
进措施,以减少相角损失,仿真结果表明,和常规陷波器相比,改进型陷波器不仅能实现机械谐振抑制,而且相角损失更小,系统的动态性能更好。

