基于机电耦合的弹性曲柄连杆机构动力学分析

马庭松

（奇瑞汽车股份有限公司，安徽 芜湖 241007）

0 引言

曲柄连杆机构是在机械工程中应用最广泛的机构之一。随着工程设计技术的不断发展，工程中应用的曲柄连杆机构的尺寸越来越小，转速越来越快，弹性动力学问题就显得十分突出。有关弹性曲柄连杆机构动力学分析,国内外学者已做了大量研究工作。文献[ 1][ 2],采用联立求解电动机电磁方程和连杆机构动力学方程解决机电耦合动力学问题，理论上较完备，但计算过程复杂，编程工作量大。文献[ 3]利用电动机输出特性研究活塞式压缩机曲轴-滚动轴承系统从起动到正常工作时的动力学行为，但只考虑了曲轴的弹性变形，其研究对象实际上是曲柄滑块机构。文献[ 4]采用有限元法分析弹性连杆机构动力学问题，选用的杆单元没有考虑到杆的弯曲变形。文献[ 5]对电动机、减速器、连杆机构系统进行了分析研究，应用数值模拟得到了刚性条件下曲柄角速度和角加速度的变化曲线。本文提出一种简单实用的机电耦合弹性连杆机构动力学分析方法。该方法没有联立求解电磁方程和连杆机构动力学方程，而是直接利用电动机输出特性，过程得到简化。

1 求解的思路

因为连杆机构运动过程中弹性变形相对于刚性运动位移是很小的，因此在研究起动过程中曲柄角速度变化规律时，构件的弹性变形可以暂时忽略不计。故本文的求解思路是：首先利用电动机输出特性，建立电动机-刚性连杆机构耦合动力学仿真模型，求曲柄从起动到额定工况时的角速度和驱动力矩随时间变化规律及作用在连杆机构上的阻力矩与曲柄转角位置之间的关系。再利用有限元法建立弹性连杆机构运动微分方程，将电动机-刚性连杆机构的计算结果作为已知条件，使用Range-Kutta求解运动微分方程，求得弹性连杆机构的动力学响应。

2 刚性曲柄连杆机构动力学分析

2.1 电动机-刚性曲柄连杆机构运动微分方程

图1为电动机-曲柄连杆机构动力学模型。电动机通过减速器将输出转矩直接作用在曲柄上。若不考虑连杆机构的弹性变形，该系统是单自由度系统，可将该电机-刚性曲柄连杆机构等效为单自由度转动模型。已知电机的输出特性，根据动能定理可得电动机-刚性曲柄连杆机构运动微分方程

图1 电动机-曲柄连杆机构动力学模

式中：Je为电动机-连杆机构的等效转动惯量，ω为曲柄的角速度，Me为作用在电动机连杆机构上的等效转矩。

根据等效前后的动能相等有得到

根据等效前后功率相等有:

式中: Md为作用在曲柄上的驱动力矩，Mf为作用在摇杆上的阻力矩。

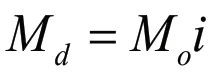
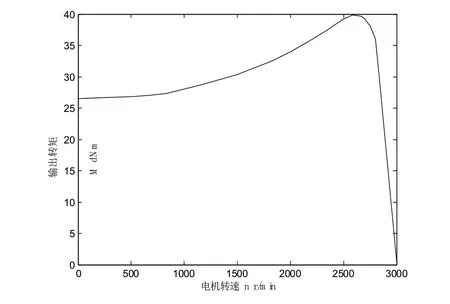
图2 电动机输出特性图

因为计算起动过程中连杆机构的动力学行为需要计算曲柄的角加速度。故由式（1）推导出曲柄的角加速度表达式：

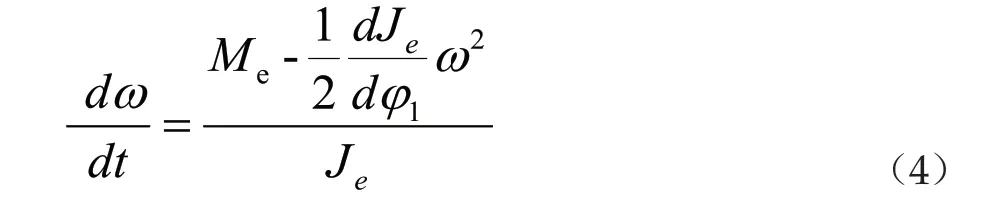
式中:1φ为曲柄的转角。

2.2 微分方程的求解

2.3 计算结果及讨论

所选用的弹性曲柄连杆机构参数如表1。

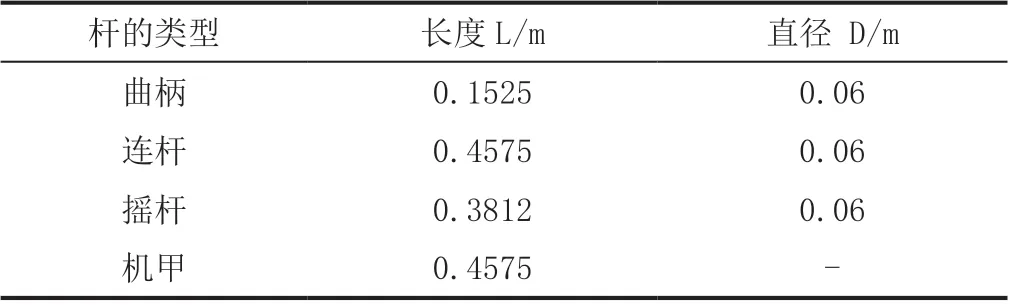
表1 机构的几何尺寸

各杆均为圆形截面杆，材料为钢，密度为7.8×103kg/m3,弹性模量为210GPa。计算采用的三相异步电动机型号为Y132D1-2，额定电压380V，额定转速2900r/min。

图（4）是从起动到稳定运行过程曲柄角速度随时间的变化关系，图（5）为机构稳定运行阶段一个周期运动过程中曲柄转速变化规律。可见，在起动阶段，曲柄角速度是呈波动的且逐渐增加的，而在稳定运行阶段，曲柄角速度是在一定范围内作非简谐周期性波动。对应的稳态转速为966.7r/min，转矩为50.6N·m。这与工程实际中的机械起动过程速度变化规律一致。

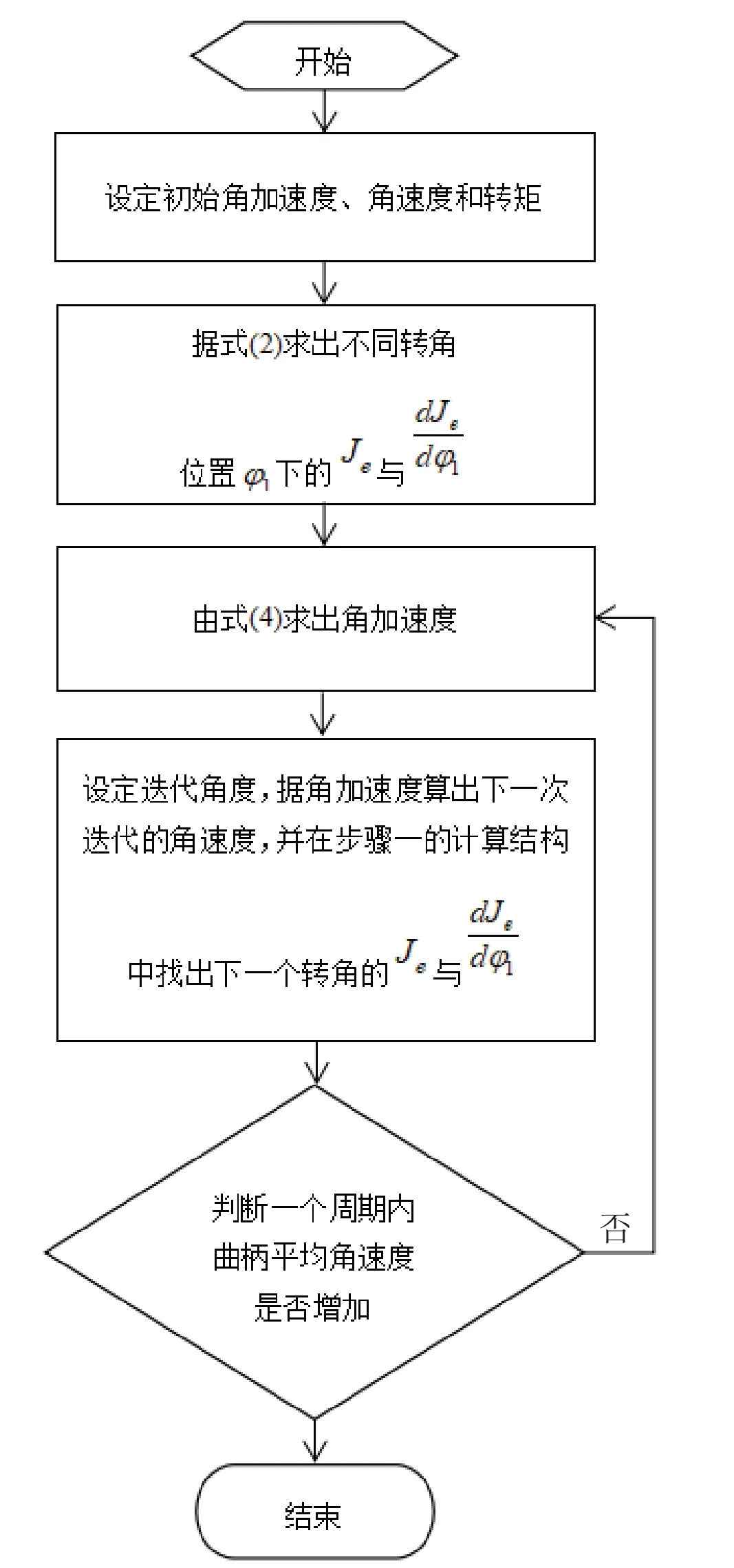
图3 刚性机构微分方程求解流程图

图4 刚性机构从起动到稳定运行运行过程

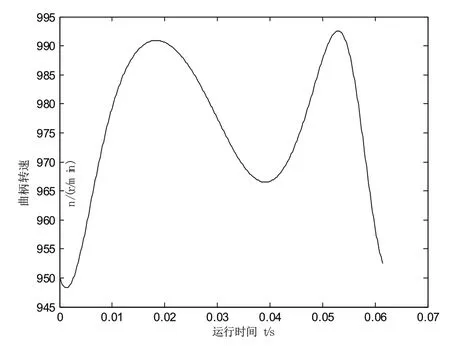
图5 刚性机构稳定运行一周期的转速变化

3 弹性曲柄连杆机构机电动力学分析

对于高速平面连杆机构或一些精密机械的连杆机构，由于其重量小，致使构件刚度降低。在这种情况下，构件的弹性变形以及由于弹性而引起的振动都是不可忽略的，因此必须研究考虑构件弹性变形的机构动力学分析问题。此问题属微分方程的混合问题，可采用有限单元法求解。

3.1 系统运动微分方程的建立

用有限单元法建立弹性连杆机构运动微分方程，先将整个机构划分为三个单元、4个节点以及选择整体坐标系下的节点位移如图（1）所示。通过单元分析可以得到在局部坐标系下的单元运动方程。

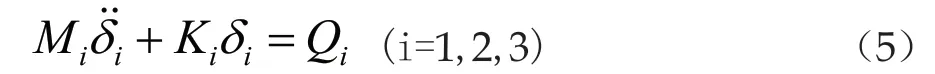
式中:δi是局部坐标系下第i个单元的节点位移向量，Qi是局部坐标系下作用在第i个单元的节点力向量，

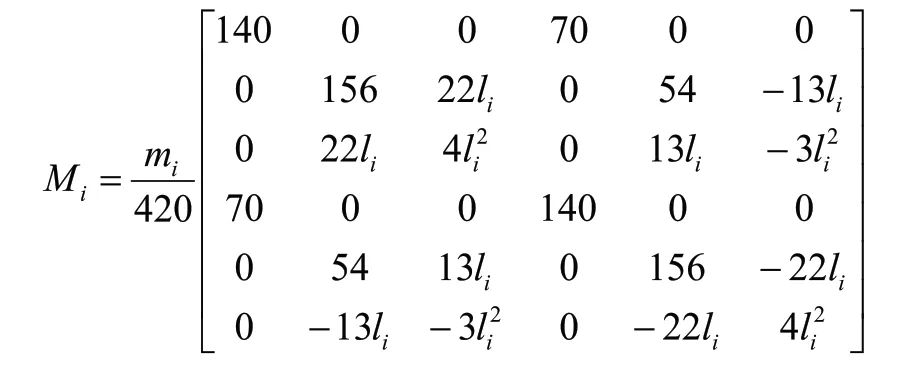
是第i个单元的质量矩阵，

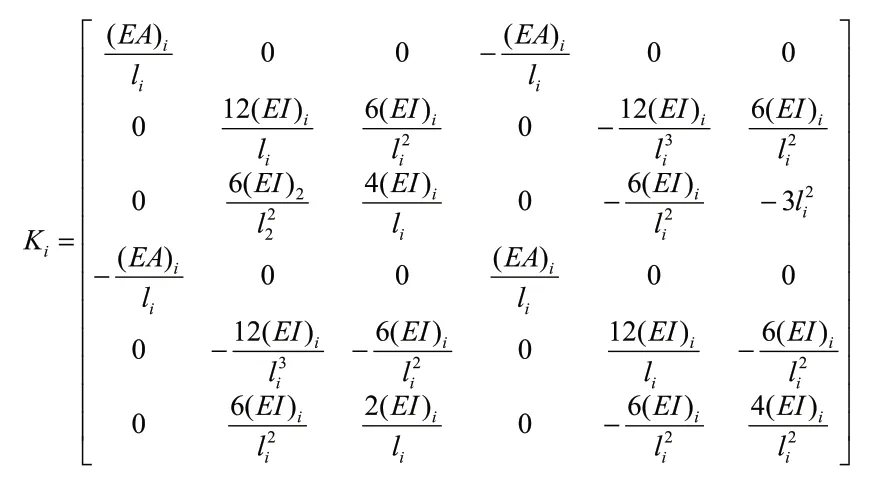
是第i个单元的刚度矩阵。

采用前处理法建立系统运动微分方程，根据边界条件消去曲柄的转动和节点O、C的位移，将13个自由度转化为9个自由度，再利用转换矩阵B将局部坐标系下的单元运动微分方程组装成系统运动微分方程，即弹性连杆机构运动微分方程。

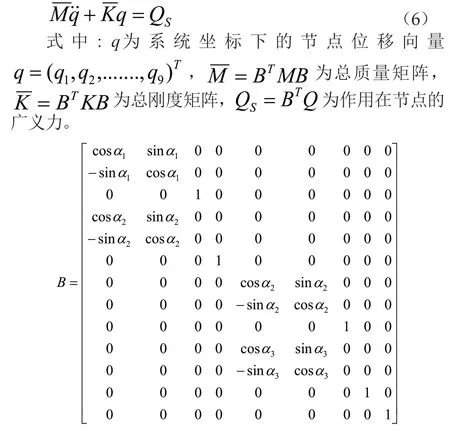
为坐标转换矩阵。

3.2 运动微分方程的求解

由于构件的弹性变形相对于构件刚性运动的位移是很小的，在数值计算过程中易被舍去，为了提高计算精度，在对系统进行动力学分析时，采用“瞬时固定法”。即在曲柄一个运动周期内，将机构瞬时固定在一系列位置上，从而形成一系列的“瞬时结构”。然后将刚性机构的运动产生的惯性力，作为外力施加在每一个“瞬时结构”上，使用Range-Kutta法求解运动微分方程，对“瞬时结构”进行弹性动力学分析，得出各构件的弹性运动。最后将刚性机构的运动与弹性运动分析结果相叠加，便得到弹性曲柄连杆机构的运动响应。

根据以上思路，图6为计算流程图。

图6 弹性机构微分方程求解流程图

3.3 计算结果及分析

图7是考虑构件弹性时摇杆转角变化曲线，其中图(a)、(b)、(c)分别为起动时、电动机输出最大转矩时(此时曲柄转速为888.7r/min)、额定工况时(此时曲柄转速为966.7r/min)曲柄转动一周摇杆变化曲线。显然，考虑构件弹性时摇杆的转角响应是

图7 考虑构件弹性时摇杆转角变化曲线

在刚性基础上叠加一个高频振动。高频振动的振幅在起动时最小，额定工况时次之，电动机输出最大转矩时最大。这是由于摇杆转角的振动与构件惯性力和作用在曲柄上的转矩密切相关。起动时转速较低、构件的惯性较小，而作用转矩也不大，所以摇杆转角的弹性振动振幅相对最小。最大转矩作用时，作用在机构上的力相对最大，而此时惯性力也比较大，所以导致摇杆转角的弹性振动振幅最大。额定工况时，因为此时惯性力最大，而转矩相对较小，故它的振幅居三者之中。另外，在摇杆的两个极限位置附近时，摇杆转角的弹性振动振幅较大。这是由于当摇杆运动到极限位置附近时，摇杆的运动方向发生变化，摇杆的角加速度较大，作用在摇杆上的惯性力和惯性力矩较大。考虑构件弹性，改变了四杆机构动力学响应规律，使得摇杆转角的振荡幅度发生变化。显然相对构件的应力也会发生变化，四杆机构的弹性动力学分析对于高速、精密机器的设计是十分必要的。

4 结语

本文研究弹性曲柄连杆机构从起动到额定工况整个工作过程的动力学行为，通过建立电动机-刚性曲柄连杆机构耦合动力学仿真模型，获得了以下结果：

（1）求出了从起动到额定工况的曲柄角速度变化规律。由于直接采用电动机的输出特性与连杆机构的动力学相结合求出起动过程中的速度变化与波动规律，计算量小、计算速度快、编程简单易行。

（2）提出了计算机电耦合的弹性连杆机构动力学分析的求解方法。可以给出从起动到额定工况时的弹性动力学响应。

考虑构件弹性时摇杆的转角响应是在刚性基础上叠加一个高频振荡。起动过程中，最大转矩作用时弹性振幅最大，将会导致构件应力最大。所以四杆机构的弹性动力学分析对于高速、精密机器的设计是十分必要的。