磨损工况下可倾瓦轴承性能研究

李 强， 唐心昊， 张 硕， 王玉君， 许伟伟， 王振波

(中国石油大学(华东) 新能源学院，山东青岛 266580)

随着石油机械行业的发展，压缩机、离心泵等旋转机械逐渐大型化、高速化，对滑动轴承性能要求不断提高，可倾瓦轴承因其高稳定性得到了广泛应用。滑动轴承性能的研究一直受到学者们的高度重视。Kayar等[1]和Li等[2]基于Reynolds方程的求解研究了偏心率、转速和润滑介质特性对轴承性能的影响。在求解Reynolds方程时耦合求解能量方程进而研究考虑热效应下固定瓦轴承[3-4]和可倾瓦轴承[5-6]性能。计算机技术的发展使求解N-S方程成为可能，Keogh等[7]开发了CFD程序，研究了轴向开槽的轴承温度分布；李强等[8-11]采用CFD方法，结合动网格技术研究了轴承动静特性以及轴承内不凝结气体；Ding等[12]基于CFD方法研究了考虑空气夹带下可倾瓦轴承的摩擦损失；Armentrout等[13]分别采用Reynolds方程和CFD方法分析了湍流及对流惯性项对可倾瓦轴承的影响；Parovay等[14]采用CFD方法研究了可倾瓦轴承性能与载荷、转速和径向间隙的关系。基于Reynolds方程和CFD方法，逐渐形成了滑动轴承热流体润滑(THD)模型。在启停或转子失稳的工况下，轴瓦发生磨损引起其形状的变化，进而改变轴承性能。磨损工况下轴承性能的研究逐渐展开[15-16]。但目前轴承磨损的研究大多为基于Reynolds方程的固定瓦轴承[17-18]，采用CFD方法的可倾瓦轴承的研究较为少见。笔者采用CFD方法、结合自编动网格程序建立可倾瓦轴承三维热流体动压润滑模型(thermo-hydrodynamic, THD)，实现润滑流场、转子运动以及瓦块转动三者之间的耦合。在此基础上研究不同磨损深度对可倾瓦轴承润滑性能的影响。

1 控制方程

1.1 流体控制方程

基于CFD方法对可倾瓦轴承三维流场进行求解，同时考虑润滑介质黏温效应及空化的影响。

质量守恒方程为

(1)

式中，ρm为混合相密度，kg/m3；vm为混合相速度矢量，m/s。

动量守恒方程为

(2)

其中

式中，p为压力，Pa；μm为混合相黏度，Pa·s；g为自由落体加速度矢量，m/s2；F为外体积力，N；ρv为气相密度，kg/m3。

转轴的偏心以及各瓦块的转动，导致轴颈与轴承之间油膜间隙分布不均匀，进而产生收敛楔和发散楔。润滑油进入轴承发散楔，油膜压力降低。当油膜压力低于润滑油的饱和蒸气压时，则会发生空化，产生气态润滑油。为了更好地预测轴承性能，采用组分输运方程描述润滑介质气、液两相组分之间的输运，表示为

(3)

式中，fk为第k相质量分数；Re和Rc分别为蒸发和冷凝速率。

质量平均速度和混合密度可描述为

(4)

(5)

式中，ρk为第k相密度，kg/m3；vk为第k相速度矢量，m/s。

组分输运方程中源项由Singhal等[19]提出的“全空化模型”计算。该模型基于多相流框架，考虑了所有一阶效应，可以处理与流体相变相关的大密度变化，而无需预先确定空化的位置、程度或类型。空化模型描述为

(6)

(7)

式中，Ce和Cc为经验常数；fg为空气质量分数；pv为空化压力，Pa。

1.2 热传递控制方程

能量守恒方程为

(8)

式中，v为运动黏度，m2/s；keff为有效导热率，W/(m·K)；hk为第k相焓，kJ/kg；Shf为体积热源项，W/m3。

流体与边界之间能量的传递采用对流换热边界条件。其热通量可表示为

q=hf(Tw-Tf)+qrad=hext(Text-Tw).

(9)

式中，q为热通量，W/m2；hf为流体侧局部传热系数，W/(m2·K)；Tw为边界表面温度，K；Tf为局部流体温度，K；qrad为辐射热通量，W/m2；hext为外部传热系数，W/(m2·K)；Text为外部散热温度，K。

润滑油黏度对温度变化十分敏感，黏度随温度升高而迅速降低。黏温效应可以用Walther[20]方程表征，其形式为

loglog(v+c)=a-blog(T).

(10)

式中，T表示绝对温度，K；c通常取0.7；a、b由40、100 ℃时润滑油黏度计算得到，分别为11.88和4.679。

1.3 边界条件及离散方法

轴承进出口边界条件为压力边界条件，进口压力为0.2 MPa，出口压力为大气压，瓦块上表面导热系数为350 W/(m2·℃)，其他为绝热，固壁为无滑移边界。基于有限体积法离散控制方程，选择基于压力求解器，压力速度耦合采用SIMPLE算法，压力差分格式采用PRESTO!。

在本文所有的计算工况下，可倾瓦轴承内流场雷诺数均小于400，因此流动状态可认为层流。为进行区分，雷诺数Ren表示为

Ren=ρvl/μ.

(11)

式中，ρ为润滑介质密度，kg/m3；v为特征速度，m/s；l为特征长度，m；μ为动力黏度，Pa·s。

由式(11)计算最大雷诺数为238.31。

2 流域模型及计算方法

2.1 流域模型

本文的研究对象为工程上应用最广泛的五瓦块可倾瓦轴承，结构参考文献[18]，轴承及润滑介质主要参数如下：轴承半径和长度分别为30和35 mm，轴瓦数为5，支点偏心为0.5，半径间隙为0.09 mm, 瓦块包角为57°, 瓦块厚度为20 mm, 瓦块转动惯量为0.000 12 kg·m2, 转子质量为55.7 kg, 转速为10 200 r/min。三维流域计算模型如图1所示，包括进油口、瓦块间间隙、油膜间隙以及瓦块背

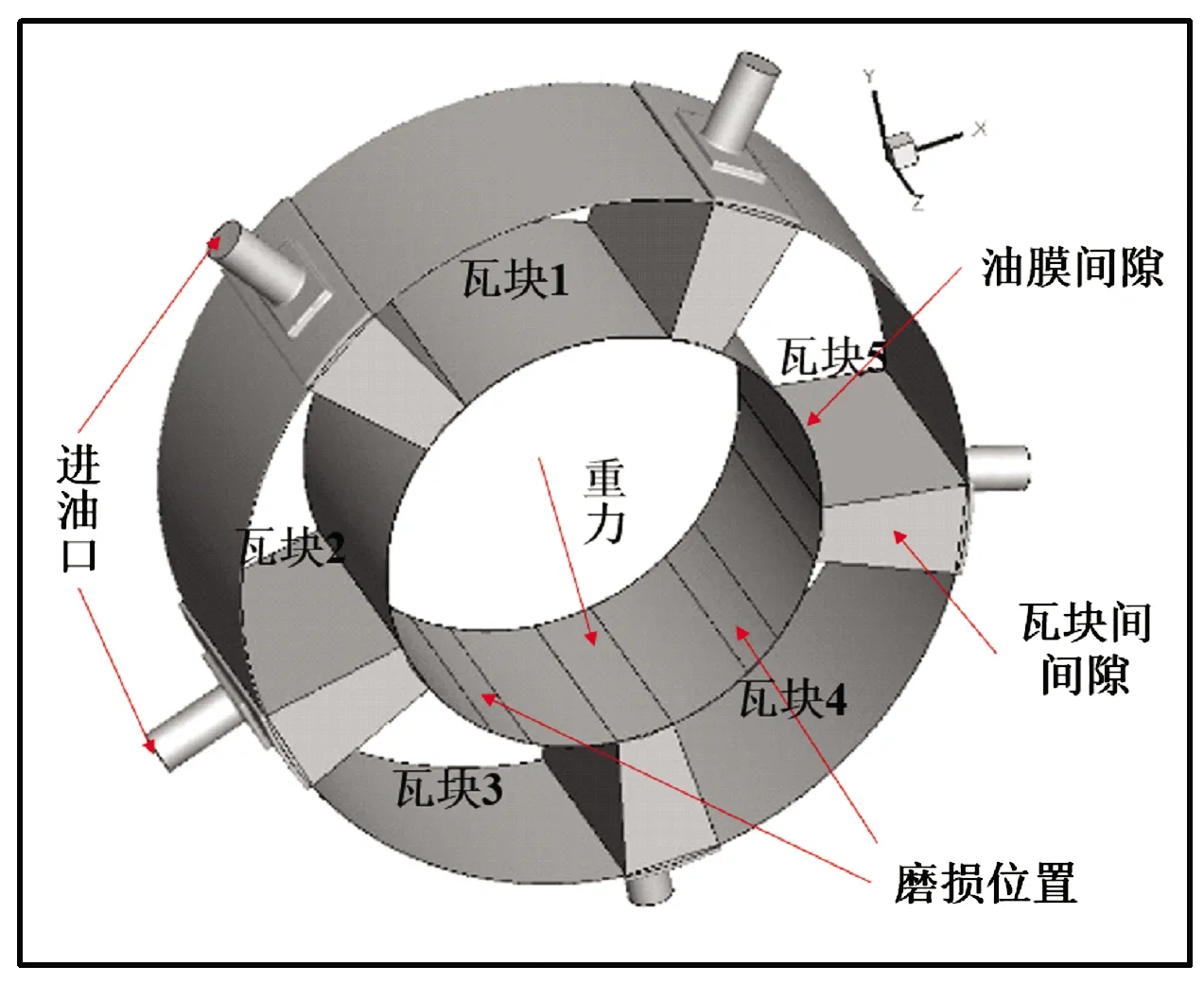
图1 流域模型Fig.1 Watershed model

部间隙等。轴承加载方式为瓦间加载，供油方式为瓦间径向供油，润滑油从轴承两侧间隙流出。32#润滑油主要参数为密度、定压比热容、导热系数、气态密度和空化压力,其值分别为860 kg/m3、2 025 J/(kg·℃)、0.129 W/(m·℃)、1.2 kg/m3和29 185 Pa。

加载瓦块油膜厚度较小，容易发生磨损。因此假设加载瓦块(3、4)发生磨损，磨损位置为瓦块上表面中心，磨损面积为瓦块上表面总面积的20%。不同的磨损程度通过磨损深度表征，磨损深度分别为10、20、30、40、50 μm。为满足网格要求，磨损边缘采用直边段过渡。瓦块磨损示意图及磨损处网格如图2所示。

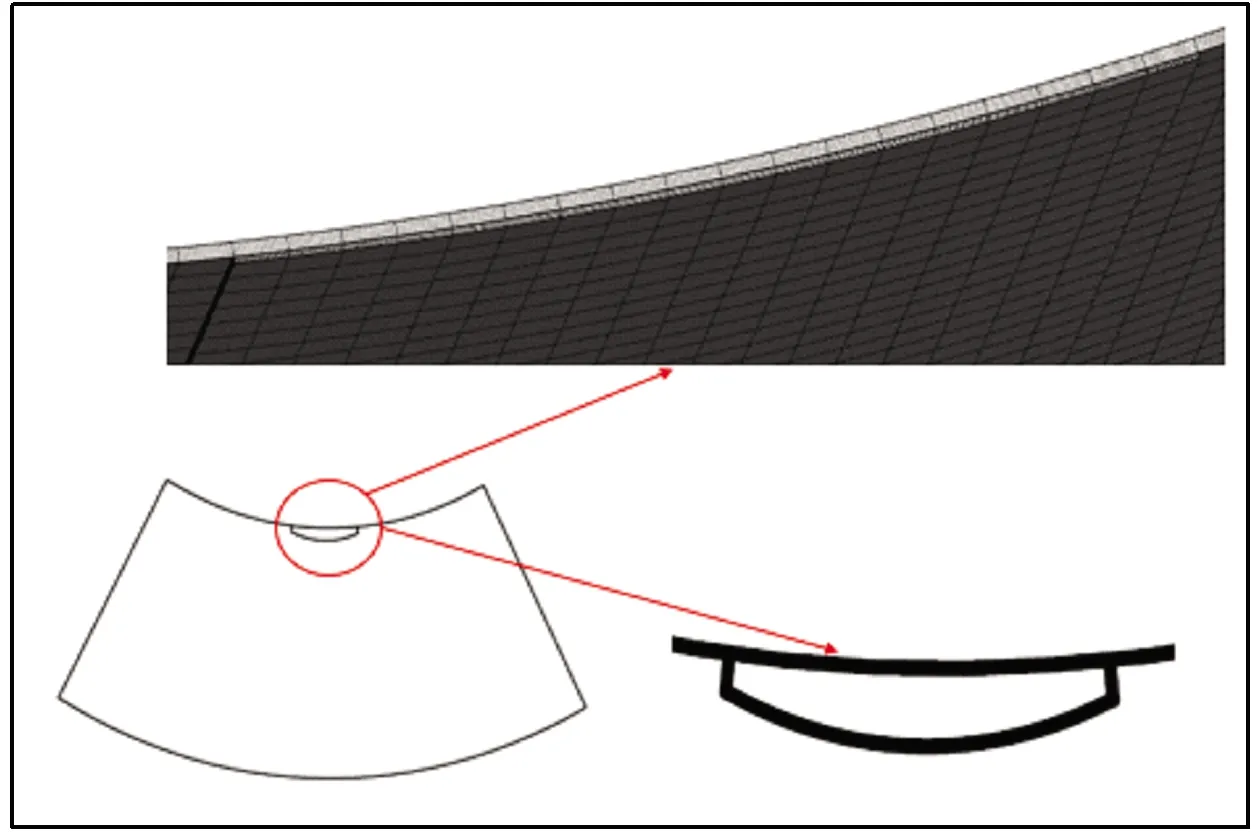
图2 瓦块磨损示意图及网格划分Fig.2 Schematic diagram and mesh of pad wear

2.2 瞬态计算过程

在转子由初始位置运动至各工况下静平衡位置的瞬态过程中，既包括转子的转动和扰动，也包括各瓦块的自由摆动。为了准确模拟上述瞬态过程，通过自编动网格程序实现润滑流场、转子运动以及各瓦块转动三者之间的耦合。

假设转子仅受到由转子质量产生的重力及轴承产生的油膜力作用。转子所受合力为零时，可认为其处于静平衡位置。其动力学方程为

(12)

式中，M为转子质量，kg；Fx和Fy分别为油膜力x、y方向的分力，N。

由转子表面油膜压力积分得

(13)

式中，R为转子半径，m；L为轴承长度，m；p为油膜压力，Pa；θ为压力与x轴正方向夹角，rad。

各瓦块绕支点的转动角速度由刚体绕定轴转动微分方程得

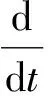
(14)

式中，Jop为瓦块对支点的转动惯量，kg·m2；ωp为瓦块转动角速度，rad/s；Mop(Fp)为瓦块受到的合力矩，N·m。

瞬态计算过程如图3所示，通过式(13)积分得转子表面的瞬态油膜力，求解式(12)得到转子x、y方向的加速度、速度及位移。由瓦块上下表面单位面积受到的油膜力及与瓦块支点的距离得到瓦块受到的力矩，代入式(14)得到瓦块的角加速度、角速度及转动角度。通过自编动网格程序(UDF)实现可倾瓦轴承网格更新及瓦块转动。瓦块转动后网格如图4所示，为更好显示网格更新效果，将轴承间隙及瓦块背部间隙放大并加大了瓦块转动角度。在转子移动和各个瓦块转动后，网格节点实现了精确移动，即使较大的瓦块转动角度也能保证较高的网格质量。

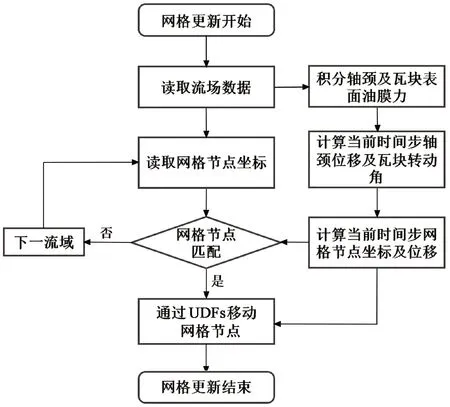
图3 瞬态计算过程Fig.3 Transient calculation process

图4 网格更新效果Fig.4 Mesh update effect

2.3 网格无关性验证

采用的动网格程序需要实时读取网格节点位置并进行更新。因此需要对计算模型进行网格无关性验证，以在保证计算准确性的同时提高计算效率。参考文献[21]，表1给出了偏心率为0.4工况下轴承最大油膜压力随油膜间隙网格数变化情况，在5层径向网格时轴承最大压力变化低于1%，因此选择径向网格层数为5层，网格数为336 000。

表1 网格无关性

3 结果与讨论

3.1 模型准确性验证

将供油温度37 ℃工况下轴承瓦块(1、3、4)最高温度数值计算结果与试验数据[18]进行对比，如图5所示。由图5可知，不同磨损深度下瓦块温度模拟结果与试验数据吻合较好，加载瓦块(3、4)温度随磨损深度增加逐渐升高，非加载瓦块(1)反之，最大温度误差出现在瓦块3，数值为2.62 ℃，小于文献[18]中瓦块1最大温度误差5 ℃，证明了采用CFD方法建立的三维THD模型可以更好地预测可倾瓦轴承性能。

图5 温度模拟与试验结果对比Fig.5 Comparison of temperature simulation and experimental results

3.2 轴承压力、温度分布

图6给出了轴承在供油温度27 ℃、未发生磨损工况下瓦块上表面压力、温度分布云图。由图6(a)可知，在未发生磨损的工况下，由于瓦块的摆动，每个瓦块均存在高压区，产生动压效应，从而提高了可倾瓦轴承的稳定性。瓦块上表面高压区沿转子旋转方向(逆时针方向)略有偏移，加载瓦块(3、4)压力明显高于其他瓦块，起主要承载作用，非加载瓦块1压力最低。由图6(b)可知，在周向方向瓦块上表面温度沿转子旋转方向逐渐升高，且在瓦块后缘处达到最高，瓦块间间隙供油，润滑油在间隙内混合使得在进入下一油膜间隙时温度得到了有效降低；在轴向方向，由于供油位置在瓦块间隙的中间，瓦块上表面温度出现了中间低两边高的现象；转子偏心导致加载瓦块(3、4)油膜厚度减小，黏性耗散更加严重，因此其温升明显高于非加载瓦块。

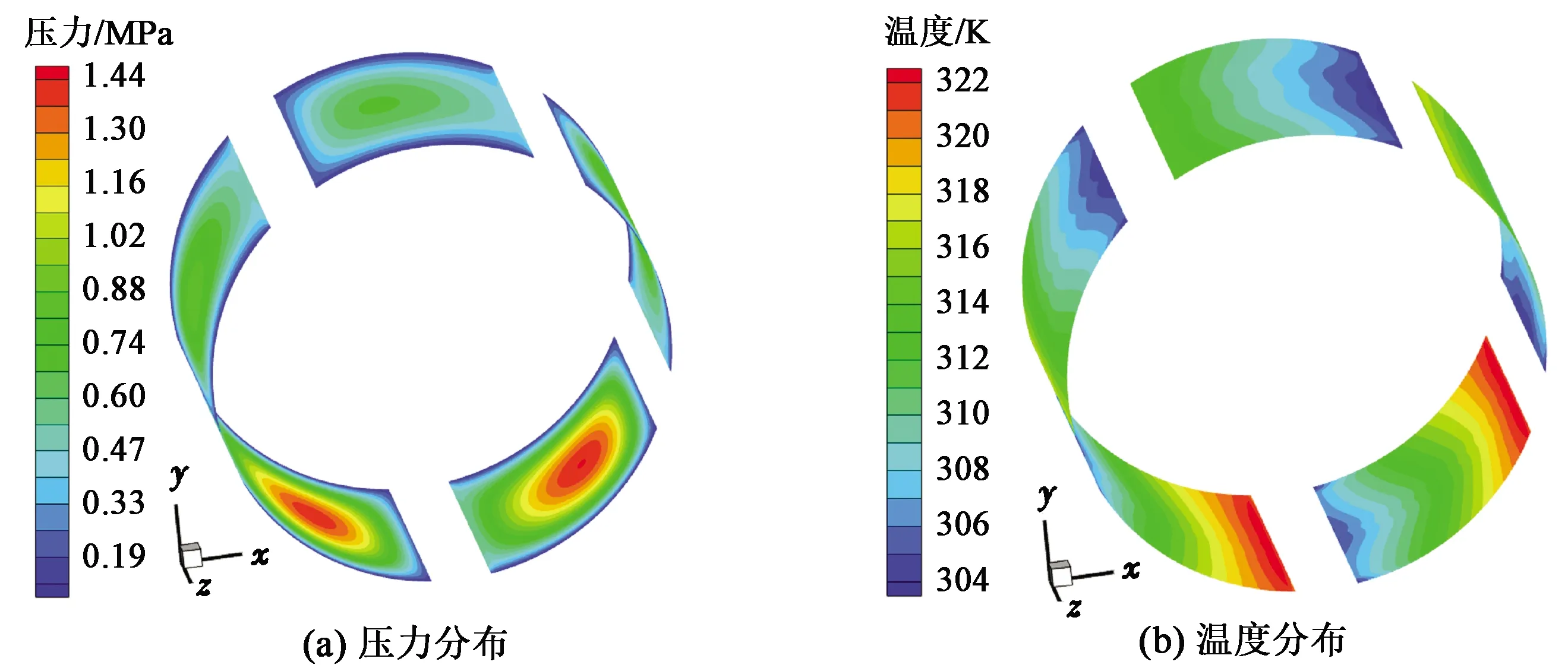
图6 瓦块上表面压力、温度分布云图Fig.6 Pressure and temperature contours of pad

3.3 磨损深度对压力、温度影响

图7给出了供油温度27 ℃、不同磨损深度下各瓦块上表面压力及温度变化，数据取自轴承中面与瓦块上表面交线，其中横坐标表示轴承圆周方向瓦块位置。

图7 不同磨损深度下各瓦块表面压力及温度Fig.7 Surface pressure and temperature of pad for various wear depth

由图7可知，在未发生磨损工况下，瓦块表面压力、温度分布连续性变化；在磨损工况下，加载瓦块(3、4)上表面压力及温度的连续性遭到破坏，且磨损深度越大连续性破坏越严重。在瓦块磨损处压力及温度产生局部降低，但与未磨损工况相比，加载瓦块最高压力和最高温度明显升高，非加载瓦块反之。随着磨损深度增加，静平衡位置逐渐下降，加载瓦块油膜厚度减小，非加载瓦块油膜厚度增大，因此加载瓦块的最高压力和温度逐渐升高，非加载瓦块最高压力和温度逐渐降低。

3.4 磨损深度对轴承承载力影响

为了研究磨损深度对轴承承载力影响，通过自编动网格程序将转子移动至偏心率0.5处，保证润滑流场、瓦块转动与转子运动之间的耦合，最终形成稳定的油膜间隙和瓦块转动角，积分转子表面油膜力即为轴承承载力。图8给出了不同磨损深度下轴承承载力，由图8可知，随着磨损深度增加，轴承的承载力不断降低，但轴承承载力的变化趋势逐渐减缓。磨损导致瓦块表面压力连续性遭到破坏并引起局部油膜厚度增大，使得加载瓦块局部压力降低，因此轴承承载力不断降低。由于磨损面积仅占瓦块上表面面积的20%，磨损深度的变化对压力的影响有限，因此承载力变化趋势逐渐减缓。在一定的磨损面积(20%)下，轴承承载力对磨损深度的敏感性逐渐降低。

图8 不同磨损深度下承载力Fig.8 Loading capacity under different wear depths

3.5 磨损深度对偏心率和静平衡位置影响

图9给出了供油温度27 ℃时不同磨损深度下轴心偏心率，由图9可知:随着磨损深度增加，轴心的偏心率不断增大，但变化趋势逐渐减缓，磨损深度在0～30 μm时，轴心偏心率变化约为10%；而磨损深度在30～50 μm时，轴心偏心率变化率约为2%。随着磨损深度增加，轴承承载力降低，因此需要更大的偏心以获得足够的油膜力支撑转子。在磨损深度为0～30 μm时，一方面，轴承承载力降低且变化较大，另一方面，在较小的偏心率下，由偏心变化引起压力升高较小，则需要更大的偏心变化获得足够的压力升高，因此在这两方面因素的共同作用下，偏心率变化较大。磨损深度为30～50 μm时，承载力变化较小，且在高偏心率下，偏心变化引起的压力升高较大，因此轴心偏心率变化较小。

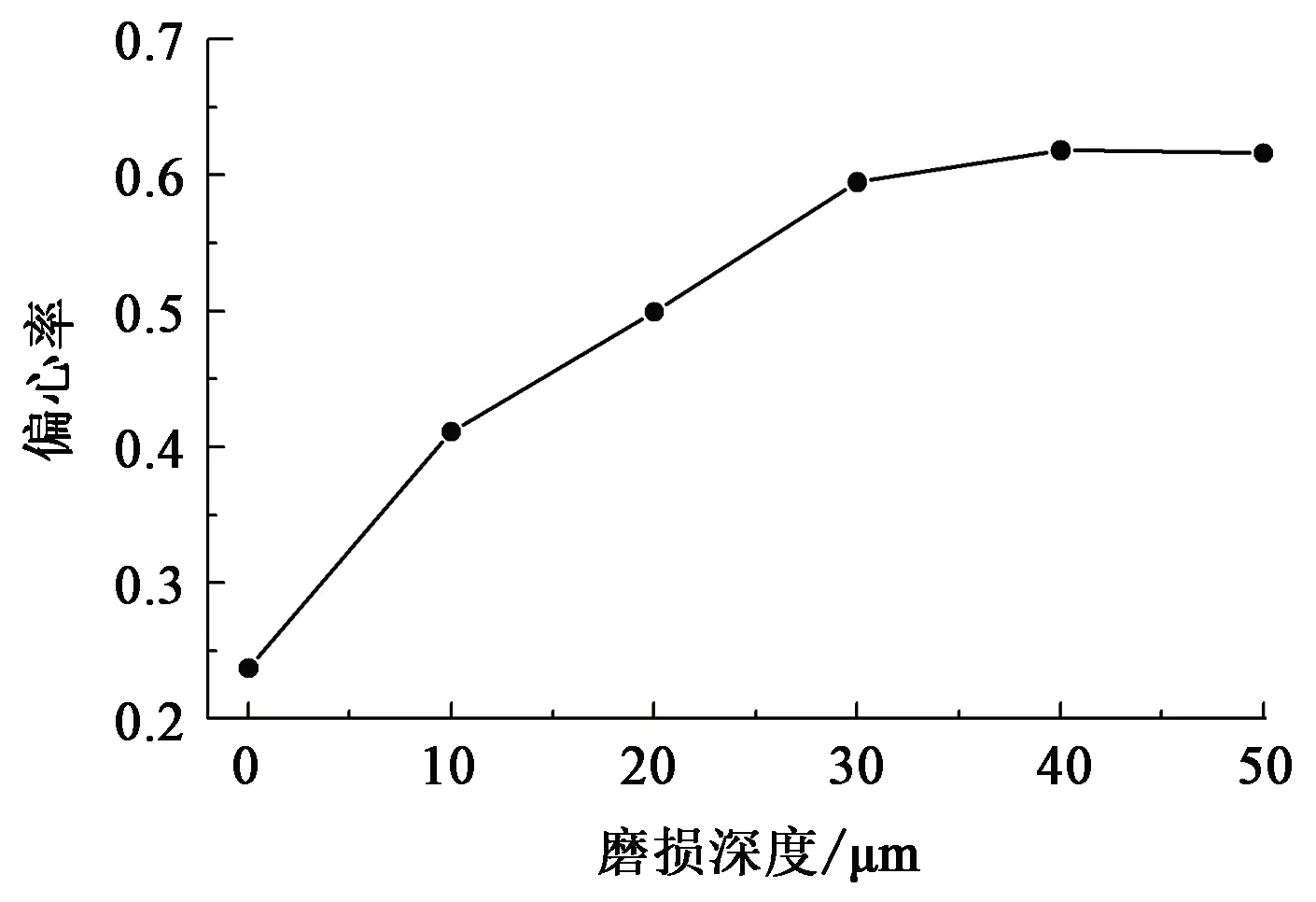
图9 不同磨损深度下轴心偏心率Fig.9 Eccentricity under different wear depths

图10给出了不同磨损深度下轴心运动轨迹。

图10 不同磨损深度下轴心静平衡位置及瓦块转动角Fig.10 Static balance position of shaft and rotation angle of pad under different wear depths

由图10可知，轴心由起始位置经过扰动后最终到达静平衡位置。随着磨损深度增加，轴心运动轨迹不断扩大，静平衡位置逐渐降低且在x轴方向先增大后减小。为进一步分析静平衡位置在x轴方向的变化，图10(b)给出了不同静平衡位置下各瓦块的转动角度。由图10可知，随着磨损深度增加，加载方向左侧的瓦块(2、3)由顺时针转动逐渐变为逆时针转动，加载方向右侧的瓦块(4、5)始终逆时针转动且转动角度不断增大，由于不同磨损深度下各瓦块产生不同的转动，改变了转子表面受力，使得轴心静平衡位置在x轴方向呈现先增大后减小的变化趋势。

4 结 论

(1)在所建立的磨损工况下可倾瓦轴承的三维热流体动压润滑模型中，通过自编动网格程序实现了润滑流场、瓦块转动、转子运动的固体-流体-固体的多向耦合计算，计算结果与试验结果吻合较好，验证了该计算模型的有效性。

(2)可倾瓦轴承每个瓦块均存在高压区，产生动压效应，瓦块上表面温度沿转子旋转方向逐渐升高，且出现中间低两边高的现象。

(3)瓦块的磨损破坏了瓦块表面压力和温度的连续性，出现了局部的压力、温度降低，磨损深度越大，连续性破坏越严重。

(4)随着磨损深度增加，轴承承载力逐渐降低，偏心率不断增大，但变化趋势逐渐减缓，轴心静平衡位置逐渐降低且在x轴方向先增大后减小。