ARIMA和GM（1，1）模型预测上海市卫生总费用

丁海峰，李立清

湖南农业大学公共管理与法学学院，湖南 长沙 410128

卫生总费用是指一个国家或地区在一定时期内（通常是指1年），全社会用于医疗卫生服务的资金总额［1］。卫生总费用作为评价一个国家或地区卫生投入水平和资金利用状况的重要指标，了解其未来发展趋势不仅可以为政府部门控制卫生总费用的合理支出，还可以为卫生部门制定医疗卫生政策提供一定的借鉴和参考。正因为卫生总费用的重要程度高，近年来，国内大量学者对卫生总费用的预测进行了探讨。李玲等［2］利用ARIMA 模型对湖南省2018—2022年卫生总费用进行预测分析；辛怡等［3］通过对我国“十三五”期间卫生总费用占国内生产总值（GDP）的比重进行预测，检验我国卫生总费用占GDP 的比重是否达到既定目标；也有学者利用GM（1，1）模型，对上海市卫生总费用及构成进行预测分析［4］。可以看出，大部分学者均是利用单个模型对我国或者地区的卫生总费用进行分析。然而现实情况中，为提高预测的参考价值，往往需要借助多个模型进行对比分析。基于此，本研究选取上海市2005—2017年卫生总费用及GDP 相关数据，分别建立ARIMA预测模型和灰色GM（1，1）预测模型，对上海市2018—2025年卫生总费用发展趋势进行预测对比分析，一方面可以提高预测的参考价值，另一方面为上海市相关部门制定医疗卫生政策提供借鉴及参考。

一、资料和方法

（一）资料来源

本研究数据来源于2005—2018年《上海市统计年鉴》，其中选取2005—2017年卫生总费用及GDP相关数据作为分析和预测指标，根据两个模型的特点，选取2005—2017年的数据建立ARIMA 预测模型，选取2011—2017年的数据建立灰色GM（1，1）模型［5］，数据的来源真实、可靠。

（二）研究方法

1.ARIMA预测模型

ARIMA 模型为差分整合移动平均自回归模型，是由学者Box和Jenkins提出的经典时间序列预测方法。在ARIMA（p，d，q）中，AR指自回归，MA指移动平均，p指自回归项、q指移动平均项数，d指差分次数。

主要建模步骤包括：①对原始序列进行平稳性检验。可通过序列图观察及单位根检验进行判断，如原始序列呈现非平稳性，则需要对其进行差分处理。绝大多数原始序列均为非平稳序列，均需对其进行差分处理。②模型的识别与检验。差分处理完成后，通过自相关及偏自相关图进行定阶，即确定p值和q值。如经过差分处理后的平稳序列的自相关图拖尾、偏自相关图截尾时，建立AR模型；当偏自相关图拖尾、自相关图截尾时，则建立MA模型；当自相关和偏自相关图均呈现拖尾，则建立ARIMA模型，通过残差值、AIC等值对比选出最优模型［6-7］。③参数估计、模型的拟合与结果预测。对所确定的模型进行参数估计，根据所选择的最优模型来检验拟合效果并进行结果预测。

2.灰色GM（1，1）预测模型

灰色系统理论认为，虽然系统是复杂、杂乱无章的，但系统是一个整体，是有序的。灰色预测就是基于灰色系统的预测，在实际预测中，多采用GM（1，1）模型，即一阶一元灰色模型预测方法，其中“G”代表Grey，表示灰色，“M”代表Model，表示模型，两个“1”分别表示一阶和一个变量的微分方程模型［8］。灰色预测模型就是通过灰色理论将毫无规律的原始数据进行累加，生成较为规律的数据，从而找出系统内在的特征及逻辑。此方法对样本含量和数据分布没有严格的要求，所需数据单一，原理简单，适用性强，其最大的特点是不需要大量的时间序列数据就能够进行预测，并取得较好的预测效果。

主要步骤包括：①进行级比的检验并对建模的可行性进行分析。②对原数列X(0)进行一次累加，AGO（累加生成）为：。③构建数据矩阵B及数据向量Y，求得预测模型方程式。④对模型预测结果进行检验。

（三）统计学方法

数据的整理与录入在Excel 软件中进行，灰色GM（1，1）模型的建立及求解在Matlab 2017 软件中进行，ARIMA预测模型的建立及求解在SPSS24.0统计软件中进行。通过描述性统计法对上海市2005—2017年卫生总费用发展现状及趋势进行对比分析。分别利用ARIMA 预测模型与灰色GM（1，1）预测模型对上海市2018—2025年卫生总费用及其占GDP比重进行预测对比分析。

二、结 果

（一）上海市卫生总费用及其占GDP 比重发展现状

由表1可知，2005—2017年，上海市卫生总费用及其占GDP 的比重均呈现不断增长的趋势，卫生总费用从362.13 亿元增长至2 087.00 亿元，年平均增长率为15.7%；卫生总费用占GDP 的比重从3.87%增长至6.81%，年平均增长率为4.83%。

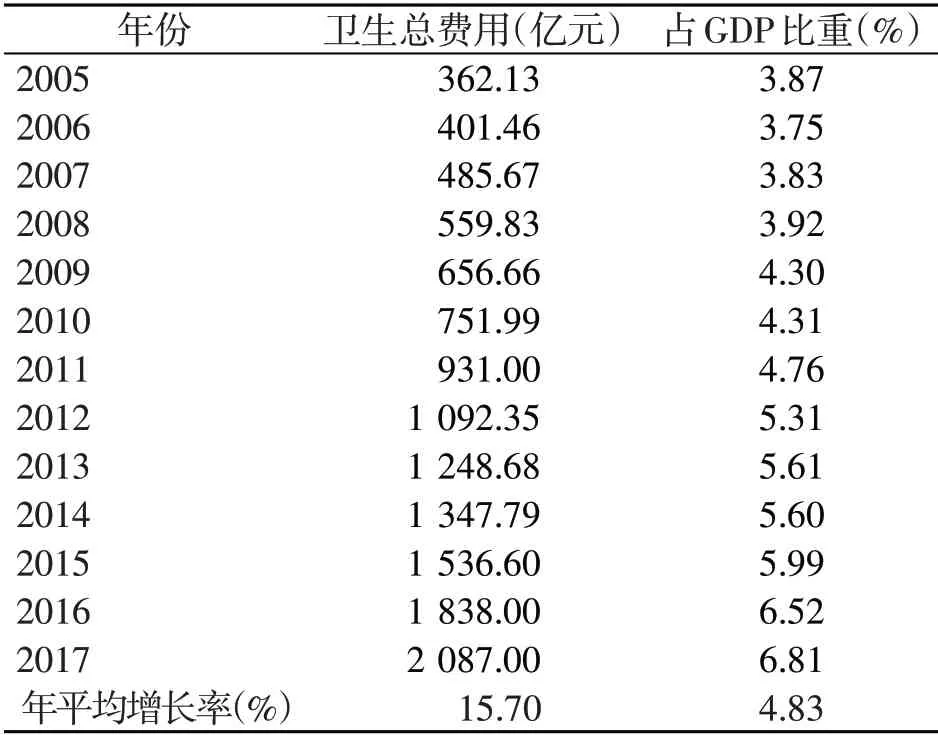
表1 2005—2017年上海市卫生总费用及占GDP比重

（二）ARIMA模型的预测过程及结果

1.数列的平稳性处理

根据SPSS24.0软件所绘制的2005—2017年上海市卫生总费用及占GDP 比重的序列图可以看出，两个指标均呈现明显增长趋势，均不是平稳序列。因此，需对其进行差分处理。经过检验分析后可知，上海市卫生总费用序列在经过2阶差分后趋于平稳，故d=2；卫生总费用占GDP比重序列经过1阶差分后趋于平稳，故d=1。原始序列及差分序列图见图1、2。

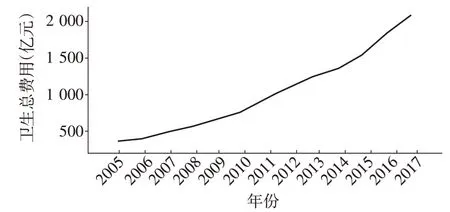
图1 上海市卫生总费用原始序列图

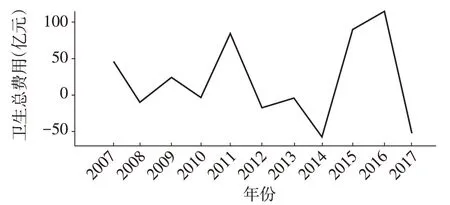
图2 上海市卫生总费用2阶差分图

2.参数的估计及检验

差分处理之后，利用SPSS24.0 软件对上海市卫生总费用及占GDP 比重分别进行拟合，通过自相关及偏自相关图初步判断拖尾和截尾情况（图3、4），经过模型的对比和不断尝试，估计ARIMA模型的各项参数，最终确定卫生总费用预测模型最优的3 个参数为p=0，d=2，q=0；卫生总费用占GDP 比重预测模型最优的3 个参数为p=0，d=1，q=1。分别建立ARIMA（0，2，0）及ARIMA（0，1，1）预测模型。经检验可知，模型的拟合统计量R2分别为0.988、0.955，R2均＞0.9；标准化贝叶斯信息量（BIC）值分别为8.311、-2.761；平均绝对误差（MAE）分别为46.948、0.196；残差的P值均＞0.05。由此可以看出模型的拟合效果较好，残差为白噪声序列，可以利用其对上海市卫生总费用及其占GDP比重进行预测。

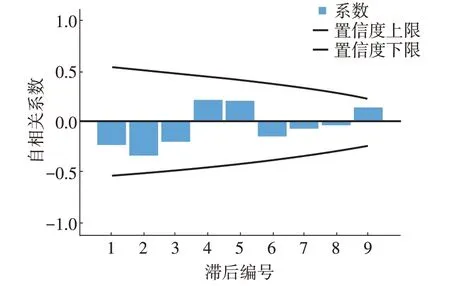
图3 上海市卫生费用二阶差分自相关

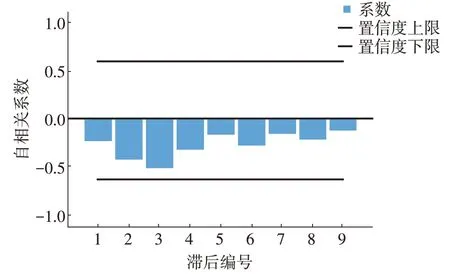
图4 上海市卫生费用二阶差分偏自相关

3.模型的拟合及预测

利用所建立的ARIMA 模型分别对上海市卫生总费用及其占GDP 的比重进行预测，并求出相对误差［相对误差=（预测值-实际值）/实际值］。经计算，上海市实际值与预测值平均相对误差绝对值仅为0.74%，说明拟合效果较好，可以利用其进行外推预测。卫生总费用预测值与实际值对比情况见表2。

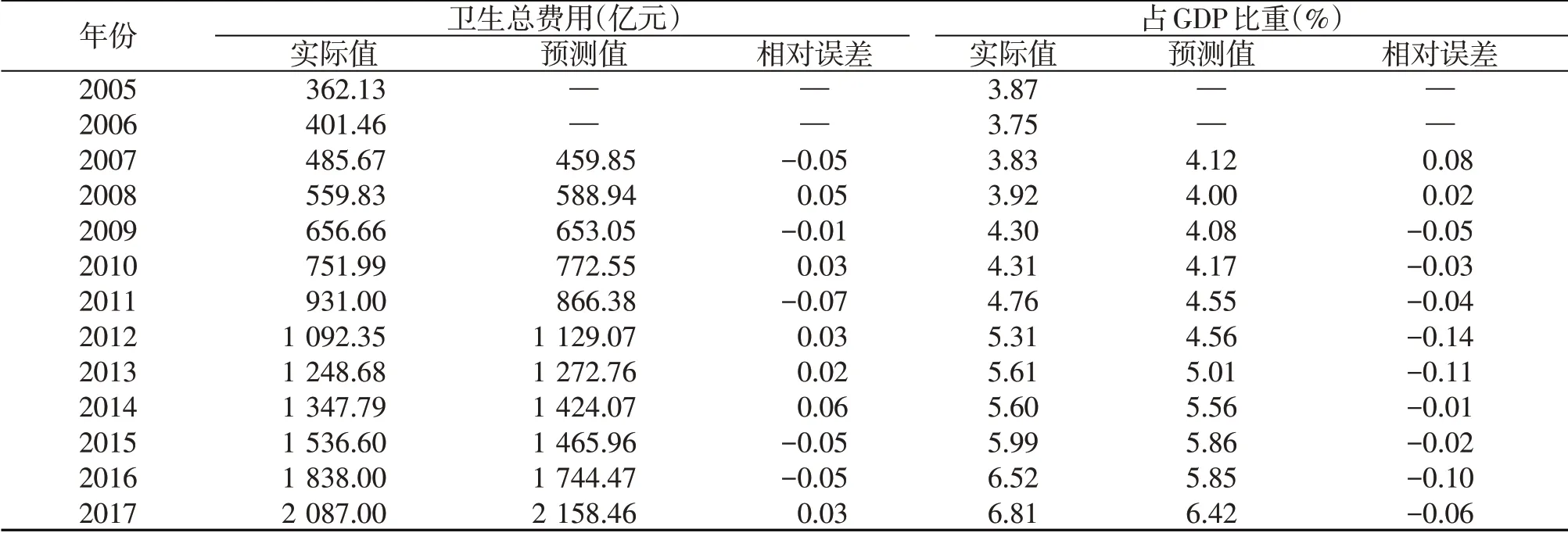
表2 上海市卫生总费用及其占GDP比重实际值与预测值对比（ARIMA模型）

（三）灰色GM（1，1）模型预测过程及结果

①建立时间序列：

X(0)=[x(0)(1),x(0)(2),……x(0)(7)]=（931.00，1 092.35，……，2 087.00）

②通过累加构造生成列：（931.00，2 023.35，3 272.03，4 619.82，6 156.42，7 994.42，1 0081.42）。

③构造数据矩阵B和数据向量Y：

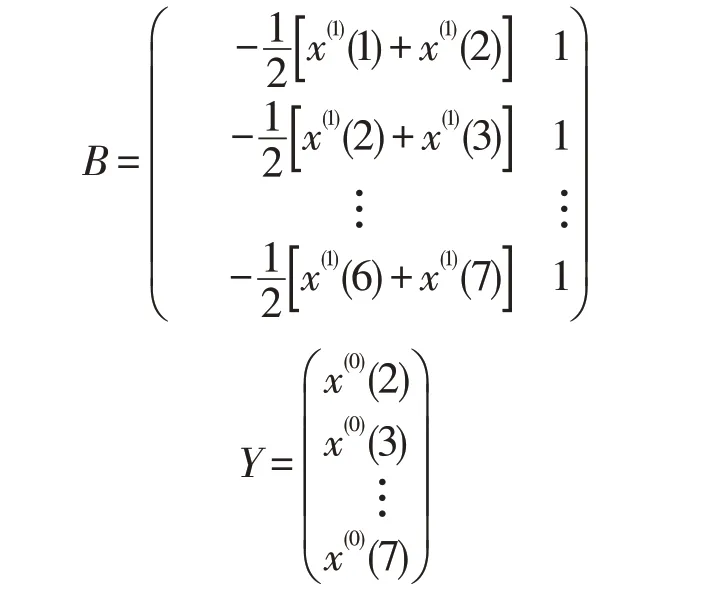
同理，上海市卫生总费用占GDP 的比重序列也通过级比检验，因此，可以建立GM（1，1）灰色预测模型。故可以计算出卫生总费用占GDP 比重的a和μ分别为：-0.051 446 433、0.048 524 838。因此，可以建立上海市卫生总费用占GDP 比重的GM（1，1）灰色预测模为：

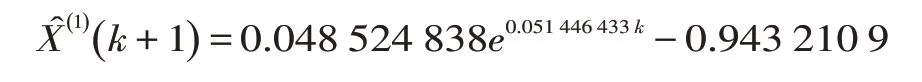
④模型的检验。经计算可知，上海市卫生总费用的平均相对误差为2.34%，后验差比值C为0.006 896 762，C远小于0.35，模型精度P为97.66%，表明模型的精度较高，同理，求得卫生总费用占GDP比重预测模型的后验差比值为：0.027 260 739，模型精度P为98.17%。经模型验证，所有C均小于0.35，由此可以表明所建立的模型精度相对较好，均具有较为科学、准确的预测效果。由结果可知，所有模型-a均＜0.3，因此可以利用所构建的模型对上海市卫生总费用及其占GDP 比重进行中长期的预测，实际值与预测值的结果见表3，具体拟合效果见图5、6。

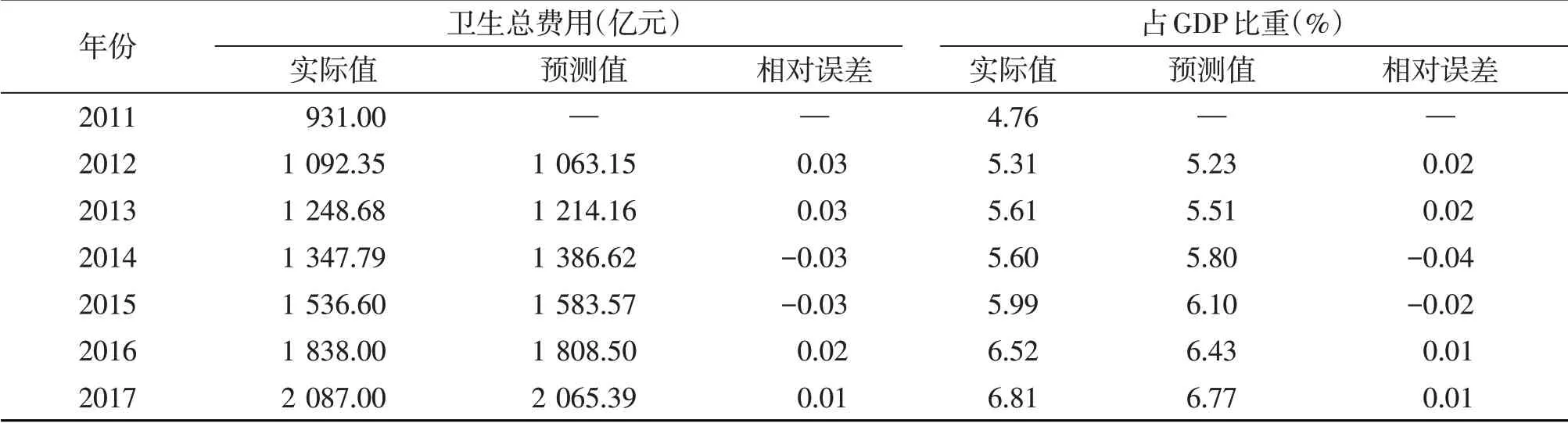
表3 上海市卫生总费用及其占GDP比重实际值与预测值对比［GM（1，1）模型］

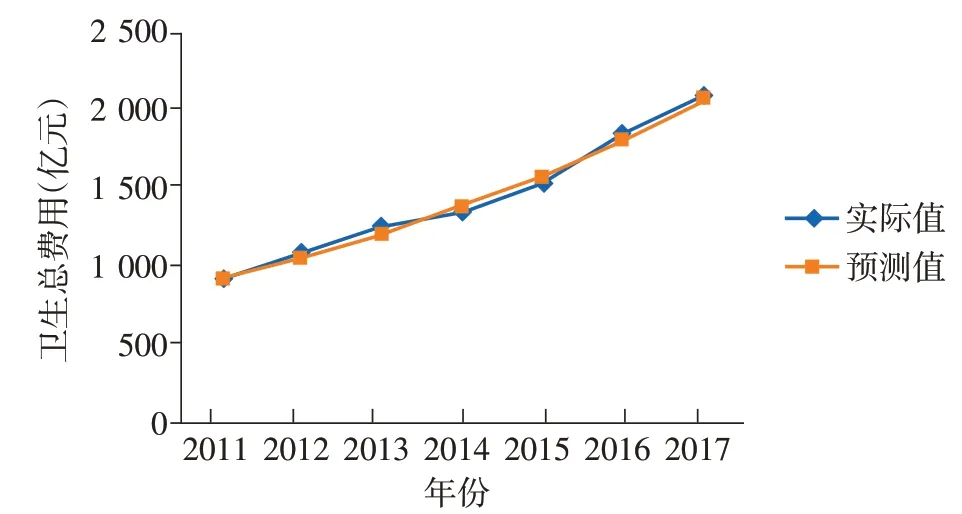
图5 上海市卫生总费用灰色GM（1，1）预测模型拟合情况

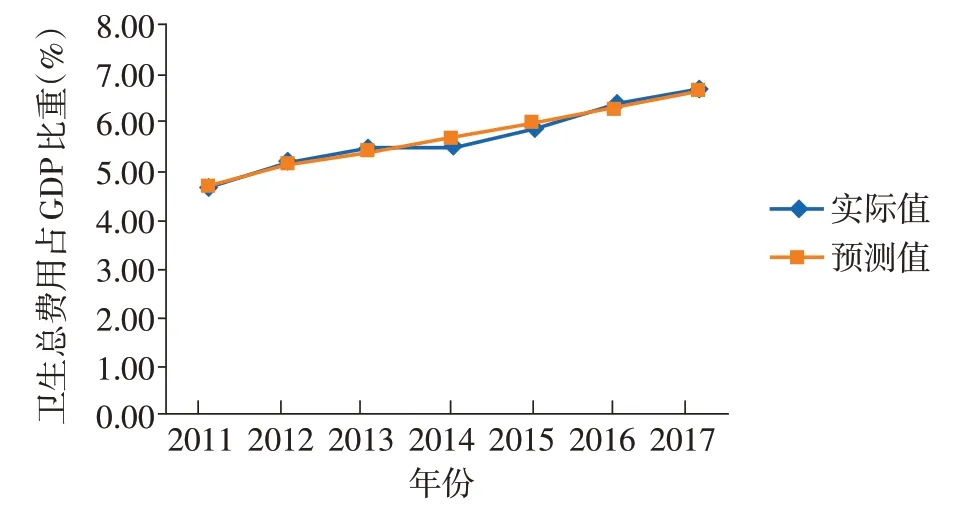
图6 上海市卫生总费用占GDP比重灰色GM（1，1）预测模型拟合情况

（四）ARIMA 模型与灰色GM（1，1）模型预测结果及误差对比

由表4可以看出，2018—2025年，上海市卫生总费用及占GDP 比重将保持稳步上升的趋势。ARIMA预测模型结果显示，到2025年，上海市卫生总费用将达到4 765.19 亿元，卫生总费用占GDP 的比重将达到8.53%；灰色GM（1,1）预测模型的结果显示，到2025年，上海市卫生总费用将达到5 976.59 亿元，卫生总费用占GDP 的比重将达到10.21%。可以看出两种预测模型所预测的结果存在一定的差距。

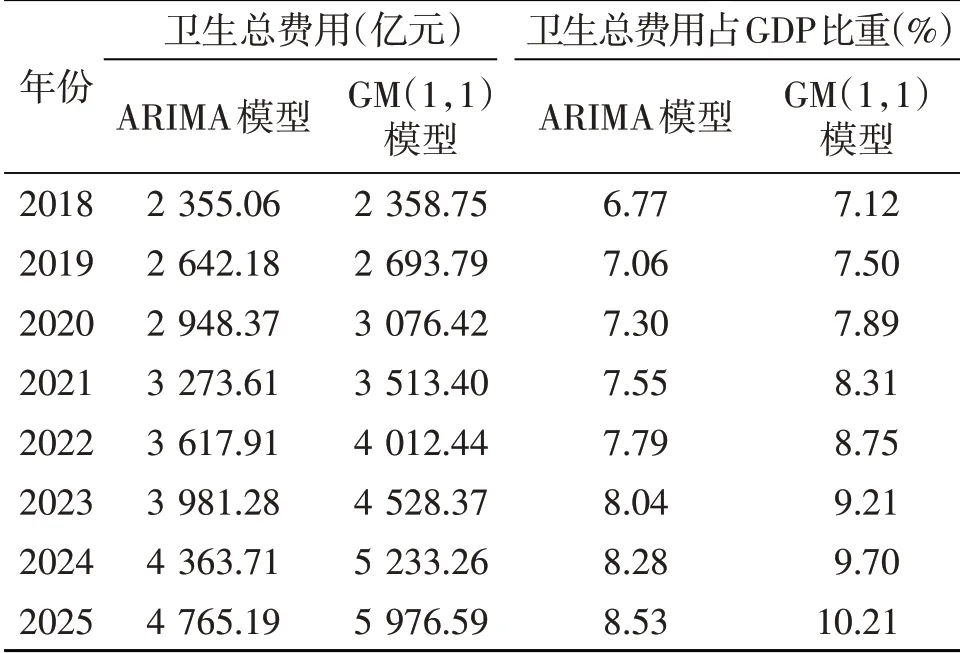
表4 ARIMA模型与灰色GM（1，1）模型预测结果

ARIMA 预测模型和灰色GM（1，1）模型的平均相对误差存在一定的差距。在卫生总费用方面，GM（1，1）预测模型的平均相对误差为0.03 亿元，ARIMA 模型的平均相对误差为0.04 亿元，GM（1，1）预测模型要小于ARIMA 模型。在卫生总费用占GDP 比重方面，GM（1，1）模型的平均相对误差为0.02%，而ARIMA 模型的平均相对误差达到了0.07%。由此可见，对于上海市卫生总费用及其占GDP 的比重进行预测，灰色GM（1，1）预测模型的预测精度及效果要优于ARIMA模型。

三、讨 论

（一）未来上海市卫生总费用及其占GDP 比重将保持稳步增长

预测结果显示，2018—2025年上海市卫生总费用及其占GDP 比重将继续保持稳步增长趋势。卫生总费用的投入水平不仅可以反映一个国家和地区医疗卫生水平的高低，还可以反映当地政府对居民健康水平的重视程度［9］。近年来，上海市不断加大卫生总费用的投入，这一方面表明上海市具有较高的医疗卫生水平，另一方面则表明当地政府对居民健康的重视。然而，卫生总费用的过快增长不仅不利于当地医疗卫生水平的提高，而且会对政府财政造成极大的负担［10］。因此，上海市相关部门在保持卫生总费用稳步增长的基础上，应该控制卫生总费用的合理增长，同时保证政府卫生支出、社会卫生支出以及个人卫生支出在合理的范围内，不断优化卫生筹资结构。此外，卫生总费用占GDP 的比重也可以反映一个国家或地区医疗卫生水平的高低。根据ARIMA 模型的预测结果，到2025年，上海市卫生总费用占比将达到8.53%，而灰色GM（1，1）模型预测结果显示，这一指标将达到10.21%。按照世界卫生组织的要求，发展中国家卫生总费用占GDP 总费用不应低于5%。因此，无论如何，两个模型的预测值都已经超过世界卫生组织规定的最低标准，其实早在2012年上海市就已经达到这一标准。虽然世界各国关于卫生总费用占GDP 比重这一指标的标准尚未统一，但至少反映卫生费用的投入水平和国民经济发展水平的相互匹配程度。因此，在今后的工作中，上海市要保持卫生费用的投入与经济发展水平恰当匹配，提高卫生效率，为居民提供更高质量、更加普惠、更有效率的健康服务。

（二）灰色GM（1，1）模型预测效果优于ARIMA模型

本研究选取2005—2017年上海市卫生总费用及GDP相关数据，利用ARIMA模型和灰色GM（1，1）模型分别对上海市2018—2025年卫生总费用及其占GDP的比重进行预测分析。结果显示，两个模型的平均相对误差均低于10%，说明所建立的预测模型精度较高，均呈现较好的预测效果。但灰色GM（1，1）模型的平均相对误差略低于ARIMA模型，这与部分学者的研究结果不一致［11］，可能与本文预测的对象以及数据周期的选取有一定的关系。根据卫生总费用预测结果，ARIMA模型的平均相对误差为0.04亿元，GM（1，1）模型的平均相对误差为0.03亿元，可以看出灰色GM（1，1）模型的预测精度略高于ARIMA模型；而对于卫生总费用占GDP 比重的预测上，两者差距较大，ARIMA 模型的平均相对误差为0.07%，而灰色GM（1，1）模型的平均相对误差仅为0.02%。灰色GM（1，1）模型和ARIMA模型是医疗卫生领域常用的预测模型，在短期预测中均有较好的预测效果［12］。然而，在现实研究中，不同预测对象的特征、属性等均有较大的差别，再加上两种模型预测原理存在一定的区别，这就导致两个模型会呈现截然不同的预测效果。因此，在今后的预测研究中，要根据不同预测对象的特点及属性，选择合适的预测模型进行分析，同时可以采用多种预测模型进行组合分析，这样不仅可以提高预测的效果和精度，还可以为决策者制定相关政策提供多种参考依据。