一种多源重力异常融合方法∗

谭斌 林沧 卢鑫

（中国船舶工业系统工程研究院 北京 100094）

1 引言

为提高重力辅助定位导航系统的精度和性能，提高重力基准图［1～2］的准确度是重中之重。目前获取海洋重力异常要素的常用方式包括卫星测量、航空测量、船舶测量重力异常［3～4］。卫星测高的常用方式包括卫星重力测量以及卫星测高反演［5～8］。卫星测量可以测出重力场的轮廓，也就是重力场的中高频信息，但是在远海应用较好，近海岸地区测量精度低。航空测量受地形地貌特征影响较大，测出的是重力场中频高频信息。船测重力异常缺点是测量方式和测量范围有限，同时受成本限制，但是可测出重力场的细节，即重力场的高频信息。本文提出的重力异常数据融合方法是基于离散小波变换原理［9～11］。为提高重力基准图的准确度，将全球重力场模型（Global Gravity Field Model，GGM）、DEM正演、卫星测高反演等不同来源的重力数据特征进行融合和提取。此外，还需要将获得的重力网格数据划分为高频和低频数据，并通过相应的系数加权采用离散小波变换的方法进行融合，最后采取离散小波逆变换方法，获取融合后的重力图谱。

2 多源重力异常数据获取方法

2.1 重力异常卫星测量获取

1）重力异常卫星测高反演获取

卫星测高仪等同于将一个测距雷达安装在卫星上，它包括时间测量系统、发射机、接收机及数据采集系统等组成部分［12～13］。卫星测高原理如图1所示。测距雷达信号经天线由发射机发出，射向地球表面，经海面或地表反射，回波信号由接收机进行接收，天线到瞬时海面的垂直距离R可通过信号传播速度Cv和往返时间差Δτ通过综合计算得出。

图1 卫星测高原理图

瞬时海面高度为h=H-R-ΔR。

其中H是卫星轨道高度，代表卫星质心与参考椭球面之间的距离，ΔR代表对流层、海况偏差、电离层、海潮、极潮、固体潮等各项改正的影响。

地球上海域面积十分广袤，有起伏的海域可以通过测高方式反演出的重力异常，常用的解析方式包括有逆维宁梅尼赛斯法、斯托克斯数值反解法、逆斯托克斯法等，每种方法各有特点。逆斯托克斯法可直接得到网格化重力图谱，而无需经全球积分获得，且几乎无边际效应；逆维宁梅尼赛斯法通过重力卫星测量技术计算垂向差值的过程中容易带入累积扰动值；除此之外，斯托克斯数值反解法因为受到边际效应方式的影响，且影响较重。因而，计算范围内越是纬度增高的地方精度值反而大大降低。

2）重力测量卫星

现今，卫星跟踪卫星SST和卫星重力梯度测量SGG是两类主要的卫星重力测量技术，SST由分为两种，包括低低SST和高低SST。目前CHAMP、GRACE和GOCE都是已发射卫星重力测量系统。但无论是SST，还是SGG都克服了传统重力测量方法的不足，采取了全新的卫星测量模式，将重力场中低频的测量精度部分进行了提升。高低SST的重力场扰动值是由相当数量的髙轨GNSS卫星跟踪低轨道卫星系统的轨道摄动而获取，与之对应，低低SST引力位变化值的获取是由相同轨道上两颗卫星间的量测相对速度变化值来获得。在已经发射的卫星测量系统中，SGG技术在GOCE卫星上得到了使用，GOCE卫星数据通过获得全球范围的髙精度、髙分辨率重力梯度图，来建立高精度重力场模型。与现有重力场模型相比，GOCE卫星数据包含了以往空间或地面重力测量中没有观测到的引力变化细节，GOCE卫星数据在高海拔和大陆地区变化剧烈。而高低SST技术在CHAMP重力卫星上得到了使用，高低SST和低低SST组合技术均在GRACE重力卫星上得到了使用。由此可见，除南北两极地区外大部分的地球区域的重力异常中低频谱数据均可通过上述两套卫星系统经由量测计算处理获取。在GRACE卫星中对三个垂直轴向的重力梯度分量进行量测，测量方法是在低轨道卫星系统中安装单多个固定基线上的差分加速度计。重力位力线弯曲变化率和水准面弯曲程度可由重力梯度的变化来表征。目前，可运用SGG技术每月对地球完成一次观测。

2.2 重力异常船测获取

1）船测重力异常特点

通过船舶测量重力变化值方式需要将测量装置（如重力仪、重力梯度仪等）安装在测量平台上，该平台可以是水面船舶或者水下潜器，从而动态观查分析测线上的重力相关数据。该方法易受机器震动噪声、以及风速、洋流、海浪以及船舶航速的影响，但同样具有观测方便直接、效率高等优点。在得出重力观测值后还需要清除在观测测量平台运动参数过程中扰动力值的影响，扰动力值主要由以下几点组成。

（1）重力仪中测量重力的敏感器件会周期性受到垂直和水平方向干扰加速度的影响，海浪、气流或机器震动等因素均可导致垂直与水平加速度受到影响。

（2）当测量平台受到垂直和水平加速度影响但相位不同时，即使当两者同频率时，摆杆型重力测量装置仍将受交叉耦合效应（即Cross Coupling Ef⁃fect）的影响，又名CC效应。

（3）受科氏力影响，测量平台由西向东航行时获得的重力值小于在同一条测线上由东向西航行时获得的重力，这种现象是由于厄特弗斯效应导致。

2）船测重力异常预处理

重力仪滞后效应补偿、重力基点比对及校正测量平台吃水校正等是海洋重力异常测量数据预处理的常用方法。

（1）重力仪滞后效应补偿

该影响可通过事先标定重力仪的时间滞后校正系数消除，目的是减少或消除因垂直干扰加速度值在重力测量装置中因强阻尼影响而导致重力测量装置测量输出值延迟滞后的现象。

（2）校对重力基点

测量平台在测量前、后分别需要在重力基准点附近进行比对，以此方法可对重力测量装置测量过程中积累的误差和零点漂移进行计算和校对，并经过相对重力值的转化，从而得到绝对重力值。

（3）重力仪零点漂移校正

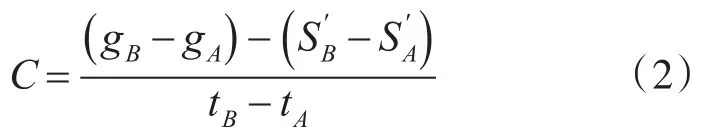
（4）测量平台吃水校正

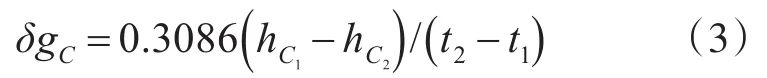
3）船测重力异常的数据处理

基于厄特弗斯效应与重力异常测量值预处理与改正完成后，才可以进行海洋重力异常的数据处理。

（1）自由空间重力异常处理

其中，测点处的绝对重力值为g；瞬时海面至重力仪高度的绝对值为h''；大地水准面到瞬时海面的高度相对值为h'；量测点的重力正常值为γ0；在自由空间内重力的异常值为ΔgF。

（2）布格重力异常处理

其中，布格重力异常为ΔgB；自由空间重力异常为ΔgF；地壳平均密度为σ；海水平均密度为σ0；测量点处的水深值是h，由平均海平面开始计算布格重力异常。因各海域分区的化学、物理性质差异过大，且声学方法测出的h会产生误差，故需对h的测量值做声速校正处理。

（3）绝对重力异常处理

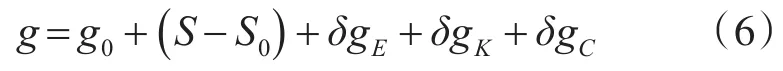
其中，重力基准点的绝对重力值为g0；测量点处的重力测量值为S；重力基准点处的重力测量值为S0；厄特弗斯效应改正值为δgE；重力仪零点偏移校正值为δgK；吃水线校正值为δgC。

2.3 DEM正演重力异常

DEM正演重力异常可用于反映重力场数据的高频特征，是理论逼近重力异常的重要方法。矩形棱柱法和Parker方法都是DEM正演重力异常的常用的方法。

1）矩形棱柱正演法

矩形棱柱正演法首先需要要把测量的空间体进行分割，这样就形成了一定数量的多面体，然后可以先计算重力空间场中某截面相对某多面体的重力场异常值，从而获得空间域重力场模型，重复积分求和累加，最终通过正演方式，获取到整个矩形棱柱体相对于重力场空间界面的重力矢量变化。矩形棱柱正演法虽然具有计算速度慢的缺点，但通过Parker方法可以在正演重力异常处理过程中引入快速傅里叶变换，从而实现等间距、一次性、大范围的DEM快速正演。所以利用矩形棱柱正演的方法计算重力异常效率是比较高的。

图2是矩形棱柱法计算重力异常方法示例。依照万有引力定律原理，设定P（x0，y0，z0）是某具有均匀密度长方体外的任意点，ρ表示长方体的密度，计算得出质量体v（x，y，z）产生的万有引力为

图2 矩形棱柱法计算重力异常

通过积分等计算和公式变化归纳，重力异常可体现为以下四种形式。

2）Parker方法

计算场源物质引起的重力场的频域公式由Parker（1973）推导出，因地质体密度为常值，设某定点的单位质量为P，通过傅里叶变换方法对式（8）两边同时进行处理：

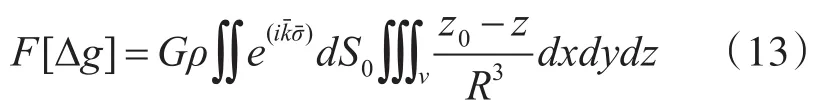
将上式整理并化简可得：

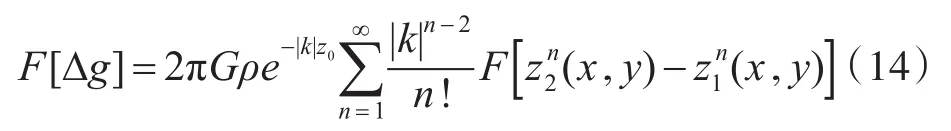
其中，F表示进行傅里叶变换；空间坐标系中的水平坐标为（x，y）；阶数是n；z1(x，y)和 z2(x，y)分别表示为地质体上界面和下界面对应的水平坐标处的高度；z0为界面平均高度；|k|为波数，定义为|k|=-ikz=2πq，且满足：

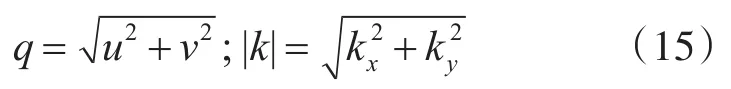
2.4 全球重力场模型融合获取

现今全球大范围区域的重力测量场均可通过重力测量技术获得，但仍然存在少部分无法测量的区域，针对已获得数据进行误差分析的过程中，发现测量误差的导致包括如地形起伏、电离层折射、空气密度误差等。地球重力场融合求和建模可以通过球谐公式进行展开如下：

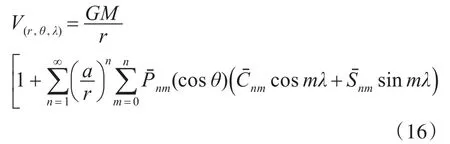
球谐展开式于正常重力位可用式（17）表示：

其中，J2n代表一个标准椭球体的物理常数值。

那么加入使用T代表全球地球重力场物理模型某点重力飘移值和既定常值之间的等效差，那么可推导出如下公式：

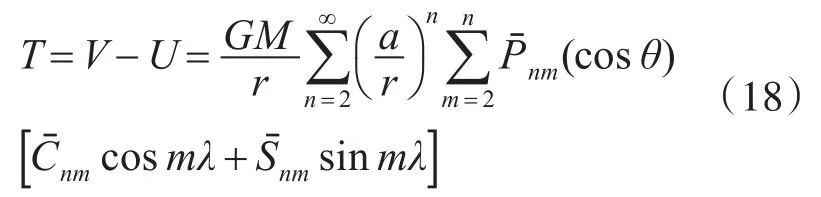
2008年，美国国家地理空间情报局（NGA）在重力异常模型EGM96的基础上，经过了勘测、拾取、建模、滤波等过程，最终公布了联合卫星测高数据、多种卫星跟踪数据的高达360阶的全球重力异常基本架构-全球重力异常 EGM2008［14］。

此外，待优化的卫星测高反演重力数据、地平面处实测重力异常数据以及GRACE卫星数据都可通过均可在EGM96全球重力场模型基础上进行迭代扩展，得出EGM2008，空间分辨率的指标也得到了极大的提升，由原本的30′×30′空间分辨率进一步提升至2.5′×2.5′，模型可展开的阶次也大幅度提升，达到2160阶，此外还提升了不用种类扰动场的逼近精度。重力场模型EGM96和EGM2008比较结果如图3所示。在现今科学探索和实际工程应用中，使用最多的全球重力场模型就是EGM2008。

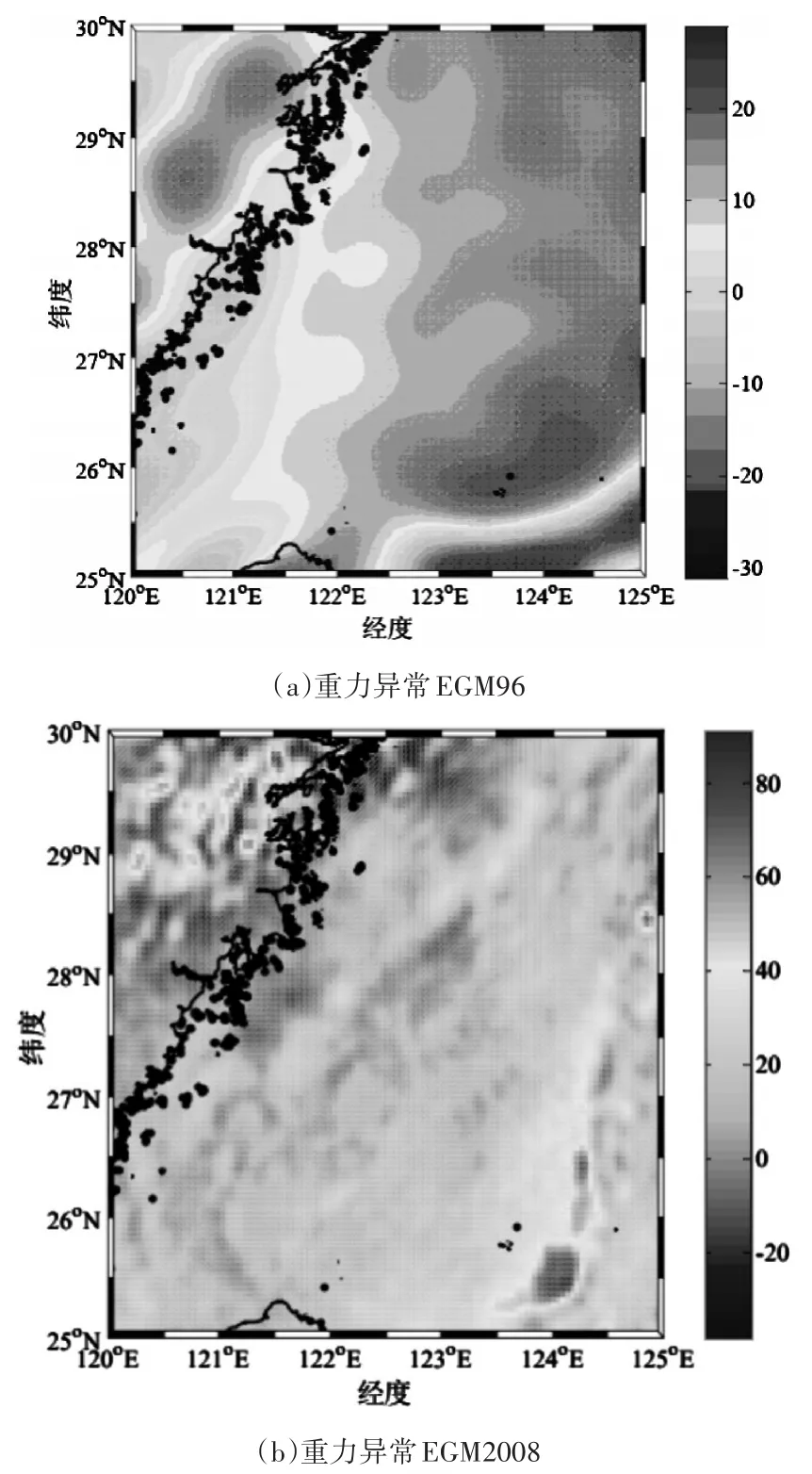
图3 对比重力场模型EGM96和EGM2008

3 重力匹配导航仿真

基于重力匹配模型，在图4中我们对重力匹配算法进行基础建模和迭代证明。潜器运行于重力模型频谱分辨精度为1′×1′的空间范围，在气象水文环境较为稳定的海域内，重力测量装置通常的测定值为0.5mGal，并且概率化表达在模型合理范围内。因惯性导航系统会受到惯性器件零偏稳定性等影响而产生漂移，定位精度误差会随着时间的增长而累积，而惯性导航系统在短时间内其定位精度却是比较高的。因此为进行重力匹配，惯性导航系统可为其提供短时高精度的航向信息。因该方法中获取的距离信息是经由惯性导航算法相邻两次采样点的位移差获得，需最大程度降低因采样点等非物理因素造成的误差模型迭代。采样过程中要不断保持潜器的航向稳定性，因而潜器最佳运动方式为在低海况海域匀速直线航行，缩短采样间隔，保持采样时间尽量精确一致，该要求对潜器较容易实现。

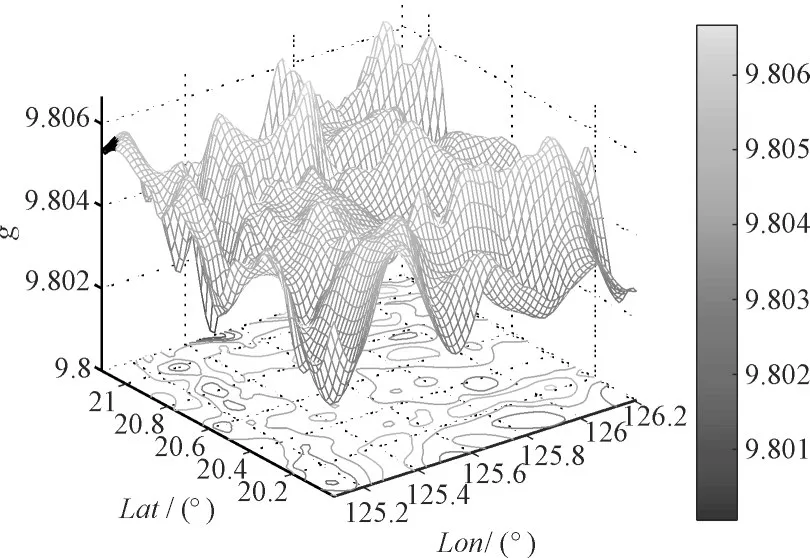
图4 匹配用重力图

重力匹配结果如图5所示。从算法的匹配仿真图和匹配建模和融合步骤中可以得出重力匹配导航方式的结果不受惯性导航惯性器件漂移造成误差累积的影响，从原理上说重力匹配导航可以归纳为无源导航的一种。在惯性导航系统运行中已经存在较大位置误差的场景下，可以进一步判断潜器是否处在重力匹配区。如已处于重力匹配区，可用重力匹配结果对惯性导航系统进行精度校正，具有相当好的位置收敛效果。

图5 重力匹配结果图

4 结语

重力匹配导航是通过实测的重力异常值与预置的数字重力异常图进行匹配计算，从而修正惯性导航系统的定位误差，是舰船导航的一种方法。该导航方式借助于重力测量、重力反演等大地测量技术的研究成果。因重力测量和匹配导航无需接收外部信息或向外部发射辐射信息，具有极高的隐蔽性和自主性，是真正意义上的无源导航，多源重力融合技术和匹配导航技术具有广阔的应用前景。