基于时间滑窗的混合Hausdorff距离航迹关联算法∗

李寅龙 张天舒

（海军航空大学 烟台 264001）

1 引言

在分布式多传感器目标跟踪系统中，每个传感器负责各区域的目标检测与跟踪，若收集不同目标的航迹序列信息，对采集到的航迹序列信息是否属于同一目标进行判断是态势统一的关键，影响着指挥员的最终决策，因此众多学者对航迹关联问题开展研究［1～2］。航迹关联算法在实际中有很多应用，例如多目标跟踪空中交通管制系统等。自20世纪70年代Singer等提出这一课题以来，学术界涌现出大批优秀的航迹关联算法，国内外学者对各类航迹关联的理论和方法进行了大量的研究［3～4］。

Hausdorff距离可用于衡量两个集合的相似程度，是集合距离的一种度量方式，文献［5］利用单向Hausdorff距离比较建筑物轮廓与最佳拟合外接矩形的相似程度，使高分辨率遥感图像下的建筑物轮廓精度得到有效提升。文献［6］利用Hausdorff距离建立配电网馈线区域两端零序电流暂态分量幅值特征匹配度，能够在不同环境下有效定位故障区段。文献［7］融合K-means思想和Hausdorff距离，解决了点云数据的空洞问题。文献［8］利用Haus⁃dorff距离对车辆交叉区域轨迹进行聚类，建立识别模型弥补交叉路口轨迹遗漏的问题。文献［9］提出加权的Hausdorff距离以解决边界区域的像素点分类问题。文献［10］提出适当排序的广义Hausdorff距离评价点云数据的几何质量。文献［11］研究了基于K-means聚类算法的胸腰椎三维图，利用Hausdorff距离比较各类脊髓三维图像自动分割方法。文献［12］利用Hausdorff距离，构建参考模型约束活动轮廓模型的收敛，提高了分割图像轮廓在噪声、杂波、遮挡情况下的鲁棒性。

以上文献将Hausdorff距离应用于电力故障排除、点云数据、医学测量、图像分割、车辆轨迹识别等各个方向，皆取得了良好的效果。本文将Haus⁃dorff距离应用于多传感器航迹关联问题，利用Hausdorff距离比较不同航迹集合间的相似程度判决航迹是否关联。由于Hausdorff距离对野值较敏感，数据波动会大幅降低航迹关联正确率，因此本文改进传统的Hausdorff距离，且引入位置、速度、方位角等信息提出了混合Hausdorff距离判决航迹关联。针对各地传感器开机时间不一致、采样频率不一致造成的时间异步问题，提出基于时间滑窗的Hausdorff距离，将传统的一对一点迹距离变为一对三点迹距离，并且加入时间滑窗以提高时间异步情况下航迹关联的精度。

2 算法原理

2.1 传统Hausdorff距离的定义

其中，ai∈A，bi∈B。

h(A，B)称为集合A到B的正向Hausdorff距离，即集合A中数据距离集合B中数据的最小距离中的最大值，同理可得，h(B，A)称为反向Hausdorff距离，h(A，B)与h(B，A)中的较大者称为两个集合间的Hausdorff距离。

2.2 基于位置的Hausdorff距离

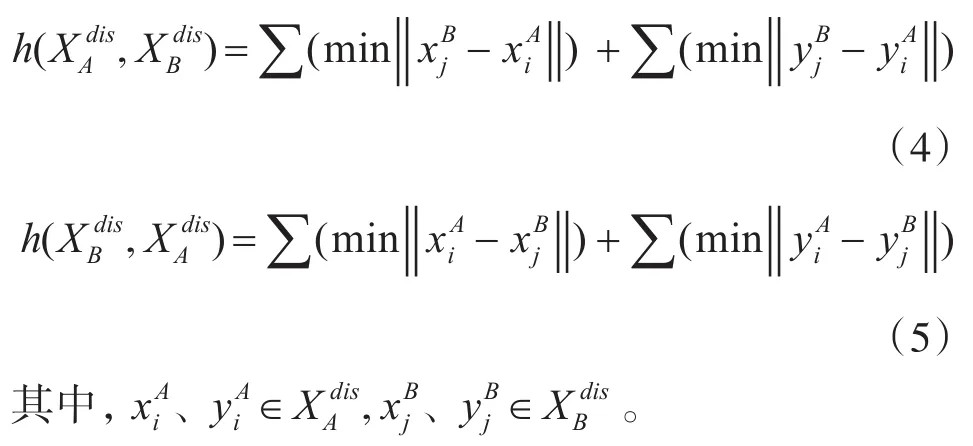
以雷达A为例，利用单向Hausdorff距离定义航迹集合间距离相似度如下：

2.3 基于速度的Hausdorff距离

在目标批数较少，航迹简单等情况下实现航迹关联较为轻松，但是在目标密集、航迹交叉、分岔、合并等情况下，易产生错关联、漏关联等情况。因此仅考虑位置因素作为判决航迹关联的标准不够全面，将航迹集合各时刻速度、方位角引入Haus⁃dorff距离，共同作为判决航迹关联的标准。

其中，t为雷达探测时间间隔。

定义基于速度的Hausdorff距离如下

定义航迹集合间速度相似度如下

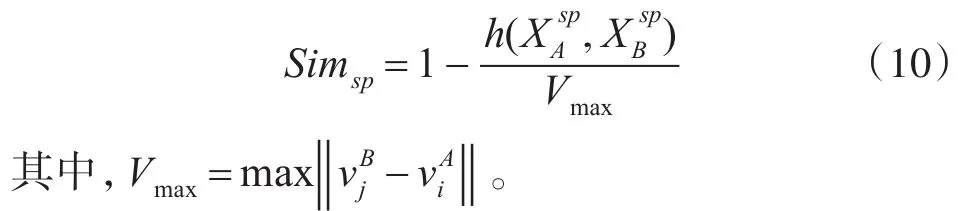
2.4 基于方位角的Hausdorff距离

当目标运动模型为匀速直线运动时，实现航迹关联较为简单，但实际情况中目标大多数做变速非直线运动，因此提出基于方位角的Hausdorff距离作为衡量航迹关联的指标之一，可提升在复杂运动状态下航迹关联的正确率。

定义基于方位角的Hausdorff距离如下：

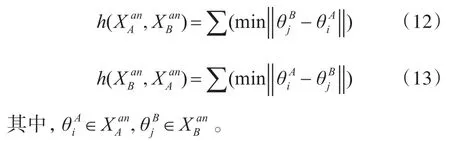
定义航迹集合间方位角相似度如下

2.5 基于时间滑窗的混合Hausdorff距离

综上所述，结合基于位置、速度、方位角的Hausdorff距离，定义混合Hausdorff距离如下：

其中W1、W2、W3为加权系数因子，W1+W2+W3=1，设置W1=0.5，W2=0.25，W3=0.25。

定义航迹集合间混合相似度如下：

其中R1、R2、R3为加权系数因子，R1+R2+R3=1，设置 R1=0.5，R2=0.25，R3=0.25。

各地雷达开机时间不一致、采样频率不同会造成时间异步，导致航迹数据错位，降低航迹关联精度。为解决此问题提出基于时间滑窗的混合Haus⁃dorrff距离，从原有的一对一Hausdorff距离变为一对三Hausdorff距离，提高时间异步情况下航迹关联的精度。

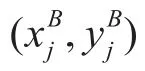
图1 时间滑窗示意图

综上所述，定义基于时间滑窗的混合Hausdorff距离如下

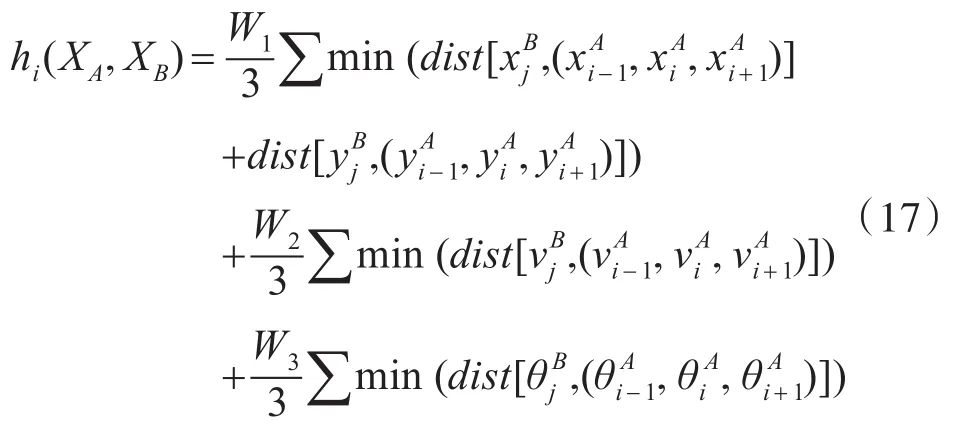
其中，dist[a，(b，c，d)]代表a与b、c、d的Haus⁃dorff距离之和。

定义航迹集合间综合相似度如下

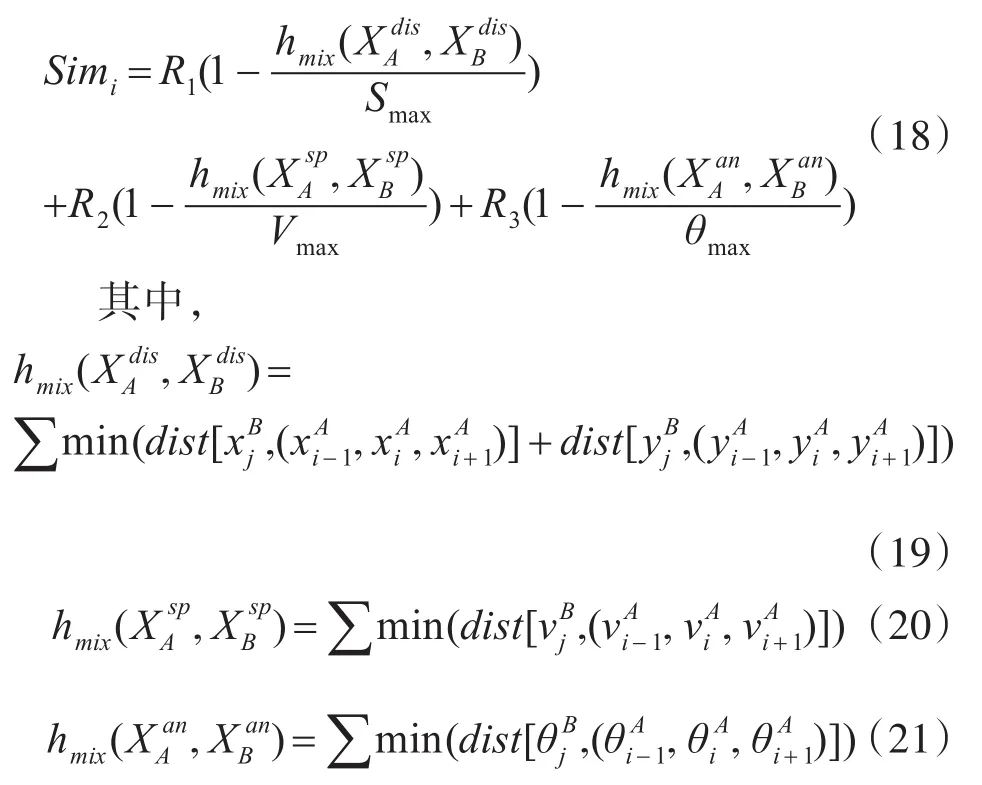
建立基于时间滑窗的混合Hausdorff距离航迹关联算法流程如图2所示。

图2 基于时间滑窗的Hausdorff航迹关联算法流程

3 仿真分析

3.1 仿真环境

假设两部异地配置的2D雷达对公共区域目标进行航迹关联，公共探测区域为边长10km*10km的矩形。雷达A的坐标为（0，0），雷达B的坐标为（15km，0）。雷达A的随机误差服从均值为0，方差为2500m2的高斯分布。雷达B的随机误差服从均值为0，方差为3600m2的高斯分布。雷达A、B每1s探测一次数据，随机生成不同批数航迹数据，进行500次Monte Carlo仿真实验。

仿真环境1：目标做匀速直线运动，初始运动速度在300m/s～700m/s之间，初始角度在0～2π之间。雷达A、B无时间异步，且数据野值已被剔除。

仿真环境2：目标做变速非直线运动，速度随机在300m/s～700m/s之间，每秒方位角随机在0～2π之间。雷达A、B无时间异步，且数据野值已被剔除。

仿真环境3：在10个目标航迹数据中随机加入3个野值，野值大小随机在原数据的0.8倍～1.5倍，其余条件与仿真环境2相同。

仿真环境4：雷达A比雷达B晚开机0.2s，其余条件与仿真环境3相同。

3.2 仿真结果

在仿真环境2的条件下，图3为正确关联率随时间、目标批数变化的曲面。随着时间、目标批数的增加，正确关联率不断下降。在时间超过7s、目标批数超过60批后正确关联率下降严重，航迹正确关联率开始低于90%。传统的航迹关联算法需要大量数据支撑，随着时间增加往往正确关联率越来越高，但本文算法对数据量没有要求，在前期数据点较少时，相比其他算法能以极高正确率完成关联，但数据点增多后航迹集合易发生交集，因此正确关联率下降。

图3 正确关联率与时间及目标批数的关系

在仿真环境1、2的条件下，图4为不同范数形式下正确关联率与目标批数的变化曲线。传统的Hausdorff距离利用2范数进行计算，仿真不同范数形式对本文算法的影响，结果表明在两种仿真环境中2范数的正确关联率最高，优于1范数和3范数。从仿真结果分析本文算法对目标机动运动状态下的航迹关联具有较强的鲁棒性，在两种仿真环境下的正确关联率相差无几。

图4 不同范数形式下本文算法的正确关联率

在仿真环境1、2、3的条件下，图5为正确关联率与目标批数的变化曲线。由于仿真环境3中加入野值，本文算法的正确关联率有所下降，但仍优于最近邻域法，正确关联率能够保持在80%以上，表明本文算法在野值环境中有较强的鲁棒性。

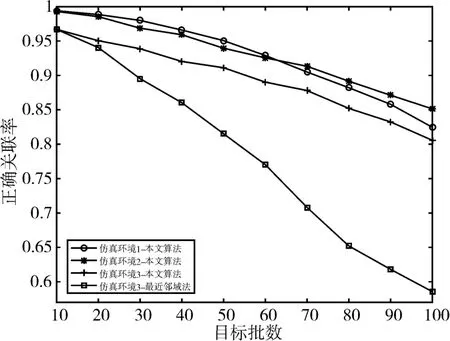
图5 不同仿真环境下各算法的正确关联率曲线

在仿真环境4的条件下，图6为各类算法在不同目标批数情况下的正确关联率曲线。仿真环境4中雷达开机时间不一致，造成航迹数据错位。随着目标批数的增加，各类算法的正确关联率不断下降，但本文算法在时间异步情况下仍能保持较高的航迹正确关联率，当目标批数达到100批时正确关联率能够保持在80%以上，仿真结果表明在时间异步、野值较多的情况下，本文算法性能优于传统的最近邻域法和灰关联法。

图6 仿真环境4下各类算法的正确关联率

在仿真环境4的基础上，改变雷达A、B的采样率之比，图7为各类算法在不同采样比情况下的正确关联率曲线。最近邻域法根据各时刻航迹点的距离判决航迹是否关联，因此对采样比较敏感，当采样比差距悬殊时精度大幅降低。本文算法及灰关联法在不同采样比的情况下仍能保持高精度关联，且本文算法的性能优于灰关联法，航迹正确关联率可稳定保持在95%以上。

图7 不同采样比下各类算法的正确关联率

4 结语

本文将Hausdorff距离应用于航迹关联问题中，改进传统的Hausdorff距离，定义了基于位置、速度、方位角的混合Hausdorff距离，在此基础上加入时间滑窗，提出了基于时间滑窗的混合Hausdorff距离航迹关联算法。仿真结果表明本文算法在目标机动、野值较多、时间异步、雷达采样频率不一致等情况下能够保持较高的精度与鲁棒性，优于传统的最近邻域法、灰关联法。