提升小学一年级学生计算能力的策略研究
陈敏纳



摘要:针对计算错误率高、计算速度慢的一年级孩子,本文就珠心算、数感的发展规律、运算模型等方面分析了一年级孩子计算能力薄弱的原因,并提出了提高一年级计算能力的若干策略,其中最为关键的是数感的培养。
关键词:数感培养 计算能力 策略
一年级孩子计算能力薄弱的原因在哪里?
1.计算能力不能单纯依靠记忆口诀
咱们不妨从珠心算说起,珠心算是用算盘为工具进行数字计算的一种方法。据说,用珠心算的方法计算速度惊人,我们来一探究竟。
如珠心算有对应的加法口诀表,如果孩子靠記忆完成大量程序化计算练习,那么显然,当孩子不再学习珠心算,过了一段时间后,孩子很容易遗忘,自然也就达不到速算的效果。更可怕的是容易让孩子产生思维上的惰性。由此可见,计算绝不是单纯地依靠记忆口诀就能学好的。
2. 没有遵循数感的发展规律
学前阶段数感的发展大致要经过下面这些阶段:笼统感知阶段→一一对应阶段→点数阶段→初步数运算→按群计数 →目测计数→成熟的数运算。孩子如果在学前阶段数感的发展跳过某一个阶段或多个阶段,或者其中的几个阶段没有足量的体验,而到了小学直接进入数的运算,显然孩子是很吃力的。
因此,孩子出现简单的计算困难核心的原因是没有建立数感。
3.没有建立丰富的运算模型
有部分孩子能熟练计算3+5得8,但填括号里的未知数,如3+( )=8,变得束手无策。事实上,加减法模型丰富多样,如减法模型就有下图中的7种,而孩子平时接触到的加减法模型可能过于单一,碰到平时没有接触过的模型,缺乏经验,自然就不擅长了。
一、提高一年级孩子计算能力的策略探讨
1.培养数感
1.1建立数字模型
从数字与数量的区别可以看出,孩子如果没有给数字赋予具体含义的能力,很难建立数与量的一一对应。那么,要培养孩子的数感,首先要建立数字模型。不妨让孩子在游戏中建立抽象的数与现实中的数量之间的关系。
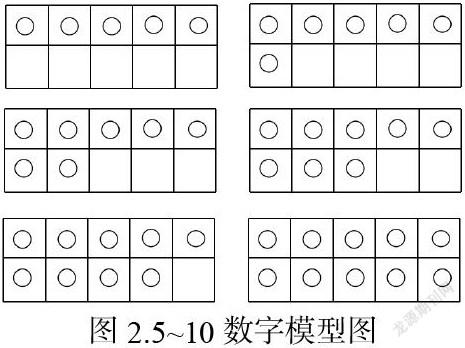
游戏一:出示一定数量的图形或物体,说出数量。孩子的水平层次分为:①手指着数;‚眼睛默数;ƒ一眼识数。遵循从少到多,孩子能很快识别10以内的数量。
游戏二:熟练掌握数字模型为数的拆分和加减法打好基础。
如随机出示类似于上图的图形,让孩子快速说出具体的数量。
游戏三:打乱的扑克牌排序复原(准备计时器)。1到10的所有花色打乱,按照思维层次有以下几个不同的水平层次。①东找找西看看没有思路;②从某一花色1开始找,依次排列1、2、3……③四个花色同时进行,每找到一个数将数插入正确的位置;④先将四个花色全部分类,再排序。四个水平层次不仅体现了数感的发展,还体现了逻辑思维的提升。
1.2建立数与数之间的联系
孩子在数与数之间如果建立了很多联系,因为有了这种联系,在不同的问题中有各种“灵活性”和“创造性”。又因为这种“灵活性”和“创造性”,使得学生不停地探索数与数之间的各种关系,这种数与数之间的熟悉感,不单是对计算能力有很大帮助,几乎对整个数学学习生涯都有莫大的帮助,比如因式分解、数列的收敛等等。例如,孩子计算9+8时不需要从1数到17,能通过自主探索出从8中分出1给9凑成10,并算出得数是17。一年级的孩子可以通过各种丰富的活动感受数与数之间的联系。
活动一:实物演示增加1个或拿走1个,经历从具象到抽象,直观体会加减的含义,理解具象与抽象的关系。
活动二:数轴理解。如8减1,在数轴上往前走是加,往后走是减,数量与格子对应,让孩子理解数字的几何模型。
活动三:翻扑克牌,黑色牌表示需要减1,红色牌表示需要加1,计算出结果。
以上三个活动均可从加减1拓展到加减几。看似慢,实则是为了快。慢的背后是数感的丰盈,为后续计算能力的提升扎下根基。
2.提升计算能力
2.1扑克牌游戏
扑克牌简单易操作,形式丰富多样。笔者特别推荐利用扑克牌训练低年级孩子的计算能力。首先,扑克牌中10以内的牌都有相应数量的图形,在计算中能无形中帮助孩子建立数与量的关系;其次,扑克牌给孩子提供了观察数与数之间的联系和关系的机会,有助于孩子创造性地进行计算,获得计算带来的乐趣。下面介绍几种常见的扑克牌计算类游戏。
游戏一:快速凑十,抽一张扑克牌,如7,想几和7凑成10,每题在一秒内反应出来。
游戏二:抽两张牌,一秒内算出相加(或相减)的得数。随着水平的提升,可从两张升级到多张扑克牌。
游戏三:抽两张牌,同色牌做加法,不同色牌做减法。
在扑克牌游戏过程中,孩子会有三个境界的提升,第一个层次是建立孩子的主动性,让孩子算3加5时是一种被动,但如果让孩子自己抽牌去算就是一种主动的学习。第二个层次是听清和理解规则,比如说抽到同色牌做加法,不同色牌做减法,这不就是教师平时反复唠叨的认真读题吗?第三层次是探索方案和建立思维能力,心算的过程恰恰要求孩子去考虑计算策略的选择,计算策略的选择过程又会要求孩子不断地对数进行重组,最终刺激孩子不停地思索数与数之间的关系。
2.2构建丰富的运算模型
美国学者富森(K.Fuson)指出,正整数加减法的现实意义主要包括以下几方面:(1)聚合;(2)比较;(3)增加性变化;(4)减少性变化。这四种情境的重要区别在于现实意义、对应的运算和两个数量之间的状态关系(前两者所反映的是两个数量之间的静态关系,后两者所涉及的则是同一数量的变化,则是一个动态的过程)。
在教学过程中,我们不难发现学生对于“动态”的数量关系较易理解,因为动态意义恰好与实际的计算过程相呼应。事实上,理解“运算”,必须考虑运算的各种丰富的现实情境,进而抽象出运算模型。因此,在情境中进行运算,孩子必须借助于具象的事物或场景,以孩子的思维活动为主的对话中进行学习,不仅有助于学生理解算理,还能促进孩子思维水平的发展。我们以图1的减法模型为例。
出示8+( )=13。
师:你能讲一个故事来描述一下这道题吗?
生:我有8颗糖果,妈妈又给我了一些糖果,我一共有13颗糖果,请问妈妈给我几颗糖果?
师:你能把它画出来吗?
引导学生先描述,再画图,后列式。每个模型的描述都不同,如图1中最后两个减法模型可这样描述。
⑥号:哥哥有8块糖果,弟弟有3块糖果,哥哥比弟弟多多少块糖果?
⑦号:哥哥有8块糖,比弟弟的多3块,弟弟有多少块糖果?
这个过程中,孩子不仅可以体会到自己的思考和创造所带来的快乐,还能不断地同化和顺应着自己接触或创造的不同概念和方法,从而促进其思维水平不断向前发展。
浙江省乐清市乐成第一小学

