球形金属膜片结构分析与多目标优化*

王佳豪, 周仕明, 李道奎*

(1.国防科技大学 空天科学学院， 湖南 长沙 410000；2.空天任务智能规划与仿真湖南省重点实验室， 湖南 长沙 410000)

0 引言

姿控系统工作环境的重力加速度趋于零，该环境下液体推进剂与增压气体容易混溶，导致燃烧不稳定.为了保证推进剂连续稳定的输出，需要对推进剂的输出进行管理.现有推进剂管理方式中，隔膜式贮箱因为安全性高、相容性好的优点，成为贮箱中的主流.隔膜式贮箱隔膜材料的好坏决定了其性能.金属材料弹塑性性能优良，是目前隔膜式贮箱中隔膜的主要材料.

在贮箱壳体内，金属隔膜因为气体压强的原因发生变形.因为膜片变形翻转过程各个位置均经历了弹塑性变形过程，部分膜片因为构型等原因，会产生褶皱、凹坑等使其失效.

现有金属膜片研究多采用有限元仿真模拟膜片翻转.其中，朱志华等[1]通过对钛制金属膜片的有限元仿真得出，金属膜片可实现重复翻转的关键是支撑结构以及壳体的限位设计.周仕明等[2]通过对铝制金属膜片的仿真分析得出，卷边区域的结构失稳是造成膜片失效的主要原因.马维力等[3]通过对钛制、铝制以及不锈钢制金属膜片进行仿真得出，钛制金属膜片翻转效果优于铝制以及不锈钢制金属膜片.周算等[4-5]通过对膜片正翻以及反翻过程进行研究，有效解决了膜片翻转过程偏心位移过大的问题并降低了翻转过程中的最大应力.

本文通过对体积为60 L的不同构型的球形金属膜片翻转过程进行仿真，分析底边半径对偏心位移以及压差曲线的影响，并对仿真中偏心位移以及翻转压差较小的构型进行了优化.

1 计算方法

因为金属膜片翻转过程变形较大，材料发生了弹塑性变形，简单的线性方程不能对其进行表征，将翻转过程的平衡方程表示为：

(1)

在此基础上，Wempner与Riks提出了一种新的计算方法——弧长法,使该问题得以解决.其是通过计算膜片翻转过程中受到的荷载、节点的位移等来获取整个膜片的状态.当载荷为λk，荷载参数的增量为Δλk，位移为xk时，相应的位移增量为Δxk，则可以写出方程

ψ(xk+Δxk,λk+Δλk)=0，

(2)

f(Δxk,Δλk)=Δlk.

(3)

式中，Δlk为增量弧长的长度.联立式(2)与式(3)可以求解出膜片节点位移xk以及载荷λk.

2 有限元模型

球形隔膜式贮箱管理推进剂的原理如图1所示，膜片受到压差作用，将推进剂挤出贮箱.球形膜片的几何示意图如图2所示，其中膜片底部半径R、预翻边半径R0、膜片高h、上部圆弧半径R1以及角度α,设圆心的坐标为(0，y).

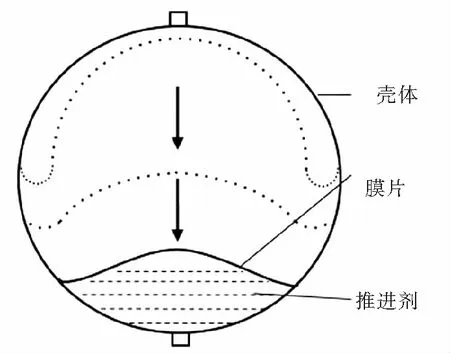
图1 球形金属膜片贮箱结构Fig. 1 The structure of spherical metal diaphragm tank

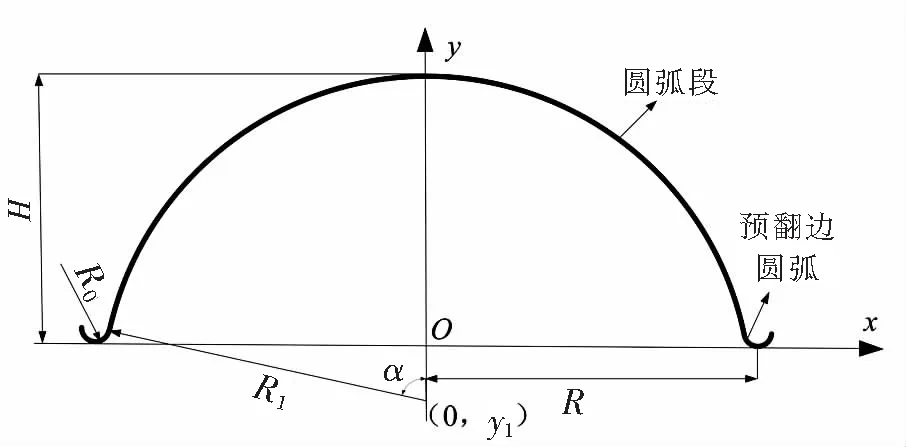
图2 膜片几何参数Fig.2 Geometric parameters of spherical diaphragm

设定贮箱体积为60 L，预翻边半径长度为5 mm，对这一给定体积下不同球形金属膜片的几何参数对膜片翻转过程进行仿真分析.设计膜片几何参数共三组，如表1所示.

将表1中的几何尺寸带入求解膜片实际容积，计算得到的体积值与设计值的误差均在1.2%以内，认为三组模型体积一致，可以进行计算分析.

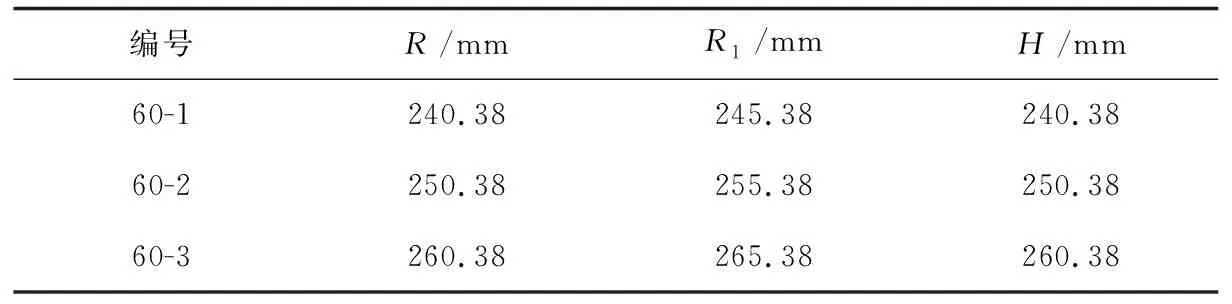
表1 膜片的几何参数

选取膜片顶点在翻转过程中偏离y轴的位移以及翻转过程中的压差曲线作为评价指标.其中，顶点偏离y轴的位移表示膜片翻转过程中的偏心程度.偏心位移越大，代表膜片翻转过程中的稳定性越低，反之则稳定性越高.膜片翻转的难易程度是通过膜片内表面与外表面的压力差来判断的.翻转过程中的压差越小表示此状态下膜片翻转越容易，反之则越困难.通过比较60-1、60-2、60-3三组构型，对膜片的翻转特性进行研究.

设置下部预翻边段膜片厚度为2.0 mm，上部翻转圆弧段膜片厚度随着高度依次递增，其中最厚的顶点厚度为2.3 mm，底边厚度与预翻边厚度相同.设定膜片的材料为钛合金，密度为4.51 g/cm3,泊松比为0.34，弹性模量为110 GPa.

图3 相同体积不同几何尺寸的金属膜片Fig.3 Metal diaphragms of the same volume and different geometrical dimensions

60-1、60-2、60-3三组球形金属膜片翻转过程的应力云图如图4所示.三组膜片翻转过程中均没有产生凹坑、褶皱等失效现象，完成了翻转过程且没有较大的偏心位移.其翻转位移曲线与压差曲线如图5与图6所示，其中60-1、60-2、60-3底边半径逐渐增大.从图中可以看出， 60-2偏心位移与翻转过程中的起始压差与最大压差最小.对比60-1与60-2可以看出，适当增大膜片的半径可以减小膜片翻转过程中的偏心位移与翻转过程中的起始压差与最大压力.对比60-2与60-3构型可以看出，当膜片底边半径过大时，膜片的偏心位移与翻转过程中的翻转压差与最大压力会增大.

图4 膜片翻转过程Fig.4 The process of diaphragm overturning

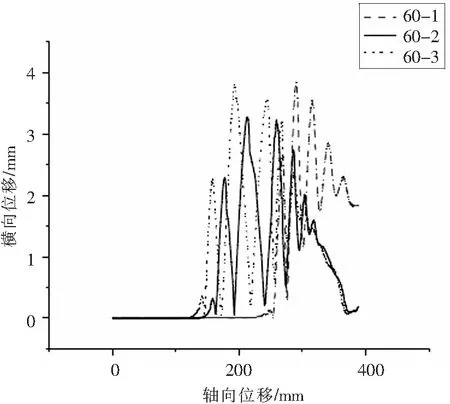
图5 膜片顶点位移Fig.5 Diaphragm vertex displacement

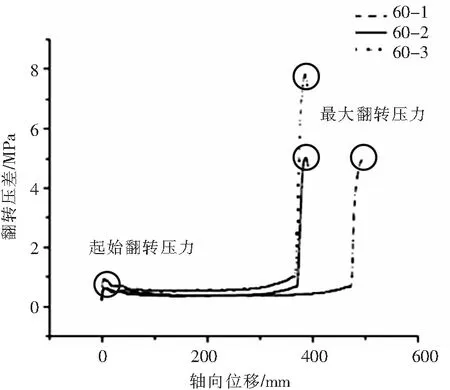
图6 膜片压差曲线Fig.6 Diaphragm differential pressure curve

3 多目标结构优化

膜片翻转过程中存在偏心、褶皱等现象，会影响膜片翻转过程，需要对膜片的构型进行优化设计，由于仿真需要花费的计算时间较长，进行多组数的分析时，时间成本较大.文章通过构建膜片翻转的代理模型，来降低仿真所需的时间成本.

代理模型是将离散的数据点进行拟合，从而推算得到离散点之外的数据值，构建代理模型的过程如图7所示.

图7 代理模型示意图Fig.7 Schematic diagram of agent model

径向基函数神经网络模型被广泛应用于拟合非线性问题.由于金属膜片的翻转过程属于高度的非线性问题，故选用径向基神经网络法构建代理模型[6].

径向基函数(RBF)的近似模型如图8所示.共包括三层前向网络——输入层、隐含层、输出层.其中，输入层与输出层的节点个数由输入数据的个数决定，隐含层节点个数与输入数据个数无关，是由拟合函数的复杂程度所决定的.

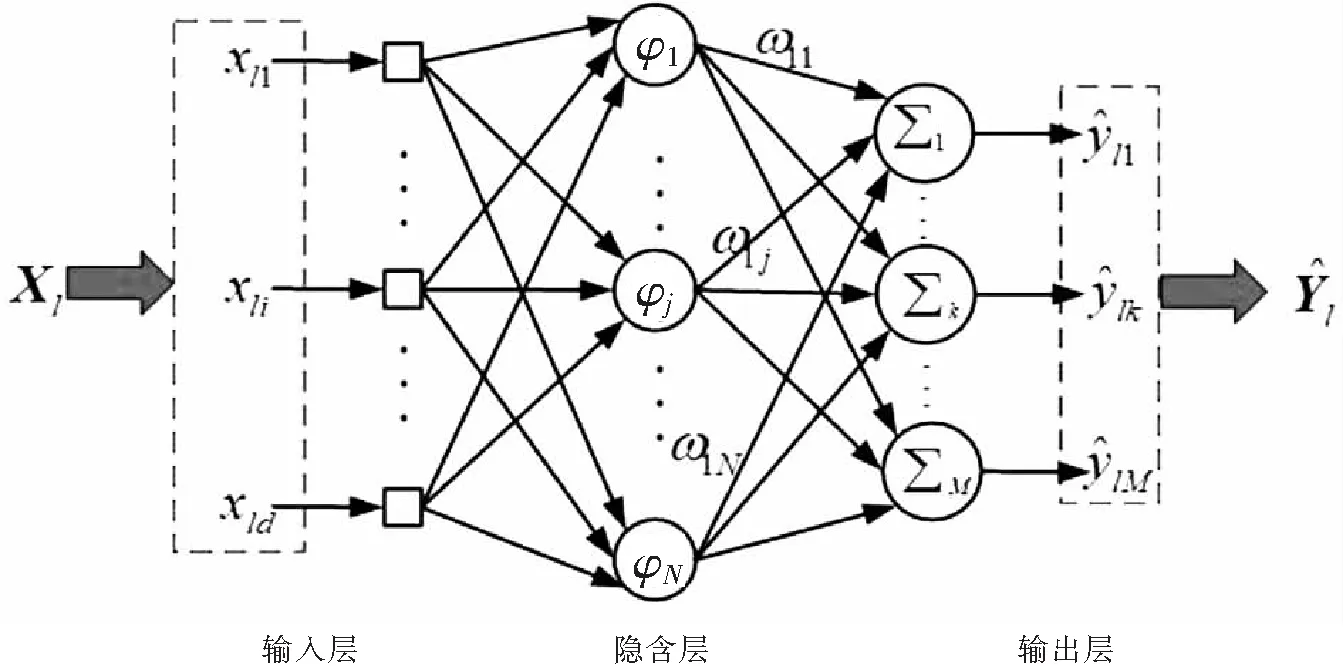
图8 RBF结构示意图Fig.8 RBF schematic diagram

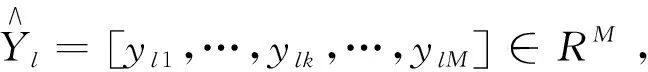
(4)

式中：N代表输入样本点的数量；X代表输入样本点的数值；Yk(X)代表基函数的第k个预测值；Xi代表样本点；ωik代表对应预测值的分量大小，其值可以通过N个样本点进行矩阵运算得到；φi代表基函数.

膜片的屈曲荷载Pbuckle表示膜片抗失稳能力，屈曲荷载Pbuckle过小时，膜片在起始翻转时，容易出现局部结构失稳.膜片翻转过程中的偏心位移Txz表示膜片翻转稳定性.本文选取膜片初始位置屈曲荷载Pbuckle以及翻转过程中的偏心位移Txz作为优化目标.研究膜片锥角α、预翻边半径R0、膜片顶点厚度d三个因素对膜片翻转过程中偏心位移Txz以及初始位置屈曲荷载Pbuckle的影响.

金属球形膜片偏心位移与屈曲载荷多目标优化的数学解析式为：

MinimizeTxz(α,R,R0,d)

MaximizePbuckle(α,R,R0,d)

Subject toR=245 mm

78°≤α≤82°

7 mm≤R0≤9 mm

2.3 mm≤d≤2.7 mm

将三因素三水平通过全因子正交实验设计共27组试验.金属膜片底边半径为245 mm，采用的材料与第二部分一致，均为钛合金，全因子试验设计表如表2所示.

表2 全因子试验设计表

从27组仿真结果中随机选取3组作为代理模型的验证值，将其余24组仿真结果拟合得到偏心位移、屈曲载荷与锥角、半径、厚度之间的代理模型.并将3组验证值代入代理模型进行验证，对比结果如表3所示.其中偏心位移Txz预测值与样本值的误差基本在10%，第3组样本值偏心位移误差较大，达到20.88%，分析认为是由于该组膜片偏心位移相对其余组别较小，导致相对误差增大，但绝对误差均控制在了0.52 mm以内；屈曲荷载Pbuckle的拟合效果较好，相对误差均在10%以内，认为满足精度要求.

表3 代理模型的预测效果

选用第二代遗传算法(NSGA-2)对构建的代理模型进行优化，设置优化起点为R=245 mm、α=78；种群的大小为24，进化的代数为20，其中交叉编译的概率为0.9.在迭代计算481次后，得出Pareto最优解集80组.在其中筛选偏心位移Txz<1.4 mm，屈曲荷载Pbuckle>6.2 MPa的共计5组，如表4所示.

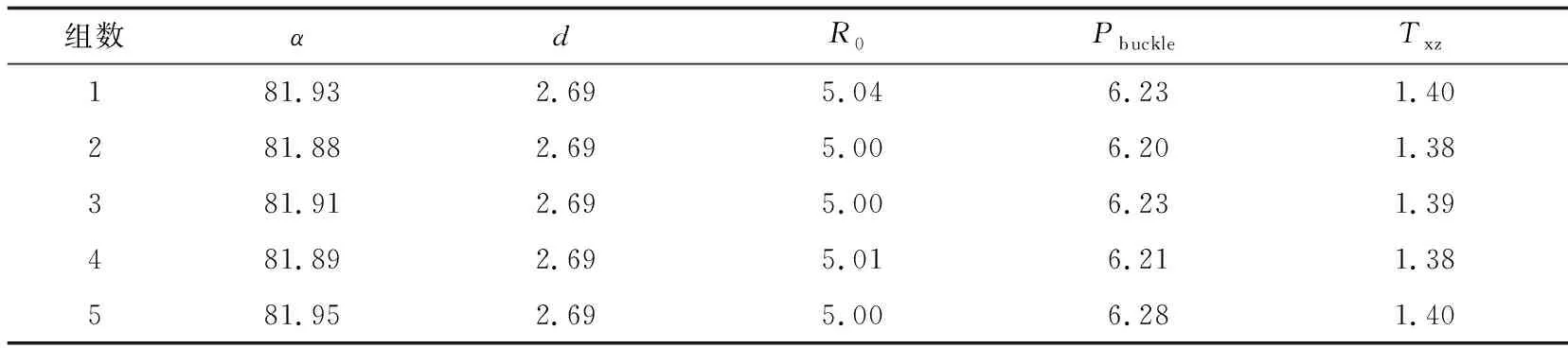
表4 经过挑选的Pareto最优解集

选取屈曲载荷Pbuckle优化效果最明显的第五组作为优化结果，与起始样本点的膜片进行对比，结果如表5所示.从表中可以看出，屈曲荷载Pbuckle相比优化之前增加了1.13%，偏心位移Txz相比优化之前减少了36.07%，优化后膜片翻转的性能更好.

表5 优化前后结果对比

4 结论

本文通过对相同体积不同底边半径的球形金属膜片进行翻转仿真分析，得出膜片底边半径与偏心位移以及压差曲线的影响，得到底边半径的较优构型；并选取锥角、膜片顶点厚度以及预翻边半径作为优化变量对该底边半径较优构型进行优化，得出结论如下：

1) 体积相同的情况下，适当增大球形膜片底边半径可以减小翻转过程中的偏心位移；但是当底边半径过大时，偏心位移反而会增大.

2) 体积相同的情况下，适当增大球形膜片底边半径可以减小膜片翻转的起始压差与最大压差；但是当球形膜片底边半径过大时，起始压差与最大压差反而增大.

3) 对底边半径为245 mm的球形金属膜片进行了优化，找到了该底边半径下锥角、预翻边以及膜片顶点厚度的局部最优解.