农用地土壤污染调查分阶段分区采样布点*

许友静， 张 清, 刘兴旺, 李 峰, 葛 飞

(湘潭大学 环境与资源学院，湖南 湘潭 411105)

0 引言

区域土壤污染调查是风险评估、修复治理和科学利用的前提，而污染调查能否有效掌握污染物的空间分布信息，其采样布点方法是关键[1-2].采样往往会结合模型模拟预测与制图来反映空间信息，因此采样数量决定空间预测精度[3]，也会影响变量的模型预测结果[4]，采样数量越多会产生越高的预测精度[5-6]，故采样数量与预测精度的定量关系是优化采样策略的重要依据，对区域土壤污染调查具有重要的现实意义.

采样布点研究是利用采样点位结合变异函数和空间插值方法对未采样区域进行预测，并根据预测误差进行采样数量的优选[7].地统计条件模拟方法是基于概率分布的思路，同时获得多个模拟结果，通过超过相关标准的概率阈值来确定污染区范围[8].序贯高斯模拟(Sequential Gaussian Simulation, SGS)适用于性质非均匀和不确定性的定量表征[9]，避免了克里格法存在的明显平滑效应[10-11].地统计学方法早已被广泛应用于土壤属性的空间分布预测，用有限的样本量对土壤属性的空间分布进行数字制图[12]，其中研究最多的是农用地变量施肥，以土壤养分的空间变异为出发点和依据，根据有限的采样点信息估算农田土壤养分分布[13].相较于土壤养分，土壤污染受自然因素和人为因素的共同作用，具有更高的空间变异性[14].目前农用地土壤污染调查的采样策略通常将整个研究区作为一个整体，再结合地统计插值结果及预测精度优化采样数，对土壤污染物空间分布的高度差异性考虑不够；在复杂地形区域仅以地形要素划分采样单元进行探讨[13]；其他采样单元的划分多以经验判断为主.

本研究基于地统计模拟和网格复合采样探索一种农用地土壤污染调查分阶段分区采样布点方法，第一阶段利用初始网格和序贯高斯模拟(SGS)不确定性分析，按照污染物空间分布差异程度进行分区；第二阶段分区布点，确定各区的合理采样数.利用收集的某乡镇农用地土壤污染数据进行模拟及验证，旨在提高农用地土壤污染调查采样布点效率，节省采样成本.

1 材料与方法

1.1 研究区概况

研究区选取南方某乡镇，区域内有一条主干河流呈西向东穿境，形成复杂的水系.地貌类型为丘陵，平均海拔70 m，亚热带季风气候，年平均气温16～18 ℃.区域内农作物主要为水稻，农用地土壤面积约159.94 km2，区域矿产资源丰富，由于长期开采导致农用地土壤污染严重.本文收集研究区内农用地土壤长期跟踪调查和采样历史数据，所有采样点分布如图1所示.

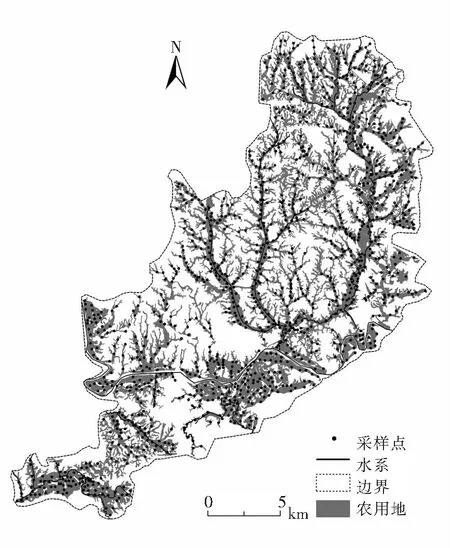
图1 研究区采样点空间分布Fig.1 Spatial distribution of sampling points in study area

1.2 序贯高斯模拟

序贯高斯模拟(SGS)是一种连续的变量序贯模拟算法，可以提供多个可能的模拟实现，根据多个模拟实现，在模拟值接近真实值的前提下再现变量的空间变化特征，能根据多个模拟实现的平均值预测变量空间分布[15].SGS多次模拟实现之间的波动性为预测结果的不确定性提供了一个定量化的途径[16]，通过局部不确定性的定量分析进行分区，空间某具体位置xm处污染物浓度的不确定性(即局部不确定性)可定义为在该位置1 000次模拟实现结果中污染物浓度低于给定浓度阈值c的概率：

(1)

式中：1 000为模拟次数；n(xm)为某具体空间位置xm处所产生的1 000个污染物浓度模拟实现结果中高于给定浓度阈值c的次数.浓度阈值选取《土壤环境质量 农用地土壤污染风险管控标准(试行)》(GB15618—2018)中相应污染物的筛选值或管控值.

1.3 分阶段分区采样策略

本研究并不进行实际采样，而是根据已有采样数据集，利用空间抽样的思路模拟抽样并进行验证，提出的分阶段分区采样布点方法包括以下步骤：

(a) 初始网格间距的设定：本研究分阶段分区采样布点基于初始网格，由于地统计学采样方法依赖于空间相关性[17]，空间相关性越强，分区效率越高[18]，故需首先确定最低有效的初始网格样点进行分区.设置1 km×1 km、2 km×2 km、3 km×3 km、4 km×4 km、5 km×5 km等5个间距的规则网格抽样，抽取靠近网格中心位置的点位，采用莫兰指数(Moran′s Ⅰ)评价得出合理的初始网格间距[19].

(b) 序贯高斯模拟不确定性分区及效果验证：将初始网格点位通过SGS得到1 000次模拟结果，依次得到超过《土壤环境质量 农用地土壤污染风险管控标准(试行)》(GB15618—2018)中管控值和筛选值的概率分布，选取概率阈值0.8，将研究区划分为污染物低值区(Ⅰ)、过渡区(Ⅱ)和高值区(Ⅲ)，SGS空间分布预测模拟过程通过GS+9.0软件完成.分区后若各区污染物浓度平均值分化、变异系数变化明显则说明分区结果比较合理[20]，若不发生显著的变化则分区结果不理想.

(c) 分区确定合理采样数及预测精度分析：各区设置0.4 km×0.4 km、0.5 km×0.5 km、0.6 km×0.6 km、0.7 km×0.7 km、0.8 km×0.8 km、0.9 km×0.9 km、1.0 km×1.0 km、1.5 km×1.5 km、2.0 km×2.0 km、3.0 km×3.0 km等10个规则网格继续模拟抽样，利用SGS平均实现预测污染物空间分布.利用10%点位作为独立点验证预测精度，得到采样数与预测精度的变化关系，预测精度验证过程及制图在ArcGIS 10.5软件完成.为了对比不分区的情况，将研究区作为一个区(О)进行合理采样数及预测精度分析.

为了验证预测精度，选用均方根误差(Root Mean Square Error, RMSE)进行评价，RMSE值越低，预测精度越高[21-22]：

(2)

式中：n为验证集样点数；oi为验证点位的观测值；pi为验证点位上的预测值.

考虑到各分区间污染物浓度差异较大，存在尺度/规模效应，使用标准化均方根误差(NRMSE)来比较各单元间的相对预测精度，较小的NRMSE值意味着更高的预测精度，NRMSE通过式(3)计算[13,23].

NRMSE=(RMSE/mean)×100

，

(3)

式中：mean为各样点集的污染物平均值.

2 结果与讨论

2.1 研究区污染物特征和初始网格确定

对研究区数据集pH和污染物浓度进行描述性统计分析，如表1所示.

表1 研究区数据集描述性统计

由表1可知，污染物变异系数(V)为79.31%，根据Wilding(1985)[19]提出的标准，CV≤15%属于弱变异，15%35%为高度变异，研究区污染物为高度变异.峰度和偏度系数表明研究区污染物总体样本数据不符合正态分布，经对数变换后服从正态分布，符合地统计学分析的要求[24].图2为5组初始网格点位的空间相关性定量分析结果.

由图2可以看出，莫兰指数值在0.5～0.88范围内，显著性检验指标Z得分在7～25范围内，说明5组网格样点的污染物含量都呈现出正的全局空间自相关性[25].但当网格间距增大时，莫兰指数值和显著性检验指标Z得分显著降低，说明网格间距越大，点位空间自相关性越弱，同时显著性程度也越低.网格间距为1 km×1 km和2 km×2 km时，空间自相关性较强且显著性程度也较高，网格间距为3 km×3 km时空间自相关性较强，显著性程度显著降低，超过3 km×3 km后，空间自相关性和显著性程度均显著降低.综合考虑相关性、显著性和采样成本，本研究选用2 km×2 km作为初始网格进行下一步的分区，2 km×2 km初始网格对应119个初始样点，符合相关研究报道[26]中准确、稳定的变异函数需要观测样点数量达到50～150个的要求.

图2 不同网格间距莫兰指数值Fig.2 Moran’s index of different initial grid space

2.2 序贯高斯模拟不确定性分区

利用序贯高斯模拟不确定性进行分区，将研究区划分为污染物低值区(Ⅰ)、过渡区(Ⅱ)和高值区(Ⅲ)，划分结果如图3所示.

图3 研究区农用地分区结果Fig.3 Agriculture sub-division result of the study area

样点的代表性高低对精度影响较大，获取代表性较高的采样点能显著提高精度，而将区域划分为变量性质较为均匀的分区后便于获取代表性较高的采样点[27].表2为各分区样点污染物含量统计结果，低值区(Ⅰ)、过渡区(Ⅱ)和高值区(Ⅲ)分别包含样本点位853个、331个、87个，平均值由分区前的0.58 mg/kg明显分化为0.36 mg/kg、0.8 mg/kg、1.88 mg/kg，表明分区后各区平均值差异显著，变异系数也由分区前的79.31%分别降低至36.11%、35.0%和26.6%，表明单元内变异显著降低，污染物浓度较为平均，分区取得较好的效果.

表2 各分区样点污染物描述性统计

2.3 各区合理采样数及预测精度分析

采样点获得的变量空间信息和代表性会对预测精度产生显著影响，但存在饱和点，达到饱和点后再增加样点并不能提高预测精度[28-29].这可能是因为采样点在空间上聚集，使空间信息达到一定的饱和程度，额外增加的样点代表性降低，即使采样点数量增加，也无法提供进一步的空间信息[30].本研究将各区饱和样点位数作为合理采样数能获得最佳效益，保证预测精度的同时避免冗余点位造成浪费.

图4(a)、(b)、(c)、(d)为各分区10组网格采样数与污染物空间分布预测精度的变化趋势和曲线拟合.由图4可知，随着网格密度的下降，各分区RMSE值呈现先基本保持平稳后升高的趋势，表明预测精度随着采样密度下降而下降，并且存在拐点可以作为合理采样数，这与Long J等[13]的研究结论一致.各区拐点有所不同，低值区(Ⅰ)、过渡区(Ⅱ)和高值区(Ⅲ)和研究区(О)拐点分别出现在2.0 km×2.0 km、0.9 km×0.9 km、0.6 km×0.6 km、0.9 km×0.9 km网格，合理采样数分别为77个、118个、56个、452个，采样密度分别为0.7个/km2、2.9个/km2、4.6个/km2、2.8个/km2.

图4 各分区预测精度(RMSE)Fig.4 Prediction accuracy of each unit (RMSE)

图5为各区采样密度与相对预测精度关系，低值区(Ⅰ)、过渡区(Ⅱ)和高值区(Ⅲ)和研究区(О)NRMSE值分别在28.97%～35.43%、18.45%～25.41%、11.75%～20.33%、38.05%～44.69%之间，随着采样密度的降低，相对预测精度分别下降了6.46%、6.96%、8.58%、6.64%，高值区下降幅度最大，过渡区和研究区次之，低值区最低.预测精度变化幅度反映了预测精度对采样密度变化的敏感度，变化幅度越大对采样密度变化的敏感性越高[13]，高值区预测精度对采样密度变化的敏感性最高，过渡区和研究区次之，低值区最低，故在污染物浓度越高的区域增加采样点数更能使预测精度显著提高.

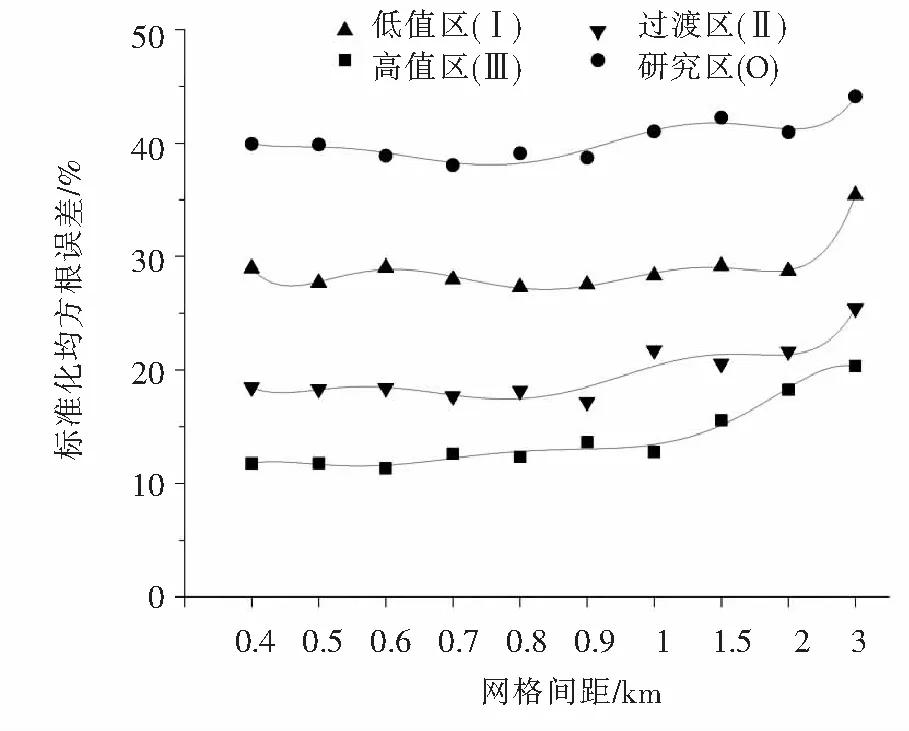
图5 各分区相对预测精度(NRMSE)Fig.5 Relative prediction accuracy of each unit (NRMSE)

进一步比较图5发现，高值区标准化均方根误差NRMSE最低，其次是过渡区和低值区，研究区最高，各区最低NRMSE分别约为12%、18%、28%和39%，表明高值区相对预测精度最好，过渡区和低值区次之，研究区最差.本研究中高值区、过渡区、低值区、研究区变异系数分别约为25%、35%、36%和79%，即空间变异最小的高值区取得了最好的相对预测精度，空间变异最大的整个研究区相对预测精度最差.多项研究表明空间变异对预测精度有负面影响[29-30]，在空间变异相对较小的区域会产生更好的预测精度，如Long J[13]通过对复杂区域不同地形下农田土壤有机质采样密度与预测精度分析发现，空间变异最大的平原台地NRMSE值最高，其次是丘陵地形，空间变异最低的河谷盆地NRMSE值最低，预测精度表现最好，与本研究结论一致.

3 结论

1) 研究区总体样本数据污染物变异系数CV为79.31%，属高度变异，经对数变换后服从正态分布，符合地统计学分析的要求；研究区合适的初始网格为2 km×2 km，此时数据基本满足空间自相关要求.

2) 序贯高斯模拟不确定性分区后平均值由分区前的0.58 mg/kg明显分化为低值区(Ⅰ) 0.36 mg/kg、过渡区(Ⅱ) 0.8 mg/kg、高值区(Ⅲ) 1.88 mg/kg，变异系数也由分区前的79.31%分别降低至低值区(Ⅰ)36.11%、过渡区(Ⅱ)35.0%和高值区(Ⅲ) 26.6%，分区方法取得较好的效果.

3) 分区确定合理采样数为低值区(Ⅰ) 77个、过渡区(Ⅱ) 188个和高值区(Ⅲ) 56个，对应NRMSE分别为28%、18%、12%，相比不进行分区(О)时合理采样数452个和NRMSE 39%，以较少的采样点取得了较好的预测精度.

4) 对比各区采样密度和预测精度发现，污染物浓度越高的分区预测精度对采样密度越敏感，污染物浓度越高的区域增加采样点数更能使预测精度显著提高；污染物空间变异越小的分区呈现越高的相对预测精度.本文提出的分阶段分区采样方法能显著减少点位，节省采样成本，提高采样效率，为管理部门农用地土壤污染调查采样布点设计提供参考.