袖带-组织-动脉系统的数值和理论求解*

许嘉诚

(上海交通大学 数学科学学院， 上海 200240)

0 引言

血压在临床上被认为是诊断和预测心血管疾病的重要参考指标[1-4].在测量血压的各种技术中，示波法是目前主流方法之一.示波法最早是由Marey[5]提出的，目前的示波算法主要分为基于振幅的方法和基于斜率的方法.基于振幅的方法通常采用最大振幅算法(MAA).目前人们普遍认为，这种方法可以准确估计平均血压，相关文献利用动脉顺应性来解释[6-9].研究人员[10-13]通常是利用特征比值来获得收缩压和舒张压，但由于特征比值是利用经验获得并且往往固定不变，因此准确性不高，误差较大.基于斜率的方法[14-15]是通过示波波形振幅包络线的斜率获得收缩压和舒张压的方法.这种方法在干净的数据中表现良好，但在实际的“脏”数据中，噪声的影响极易产生较大的误差[14].

事实上，要想提高示波算法的精度，理论研究是必不可少的.由于理论分析的重要性，越来越多的学者投入到示波算法理论研究中.例如，Babbs[16]将动脉壁模型与袖带模型相结合，以模拟袖带压力振荡，并通过回归算法来提取收缩压和舒张压.由于组织的力学性能对应力传递效率有着重要的影响，一些学者在前人研究的基础上增加组织的影响[17-19].Ursino等[17]提出袖带-手臂-动脉系统的数学模型，以研究生物力学因素对测量的影响.梁等[19]构建了与骨结合的三维袖带-手臂-动脉系统，获得其应力分布.

基于前人的研究，本文将对袖带-组织-动脉系统做相应的数值和理论分析.本文的结构如下：第1节介绍数学模型；第2节介绍基于虚功原理和基于有限元法的数值算法；第3节是量纲分析和单元分析；第4节是基于平移不变性的理论验证；最后一节是未来展望.

1 模型建立

在建立袖带-组织-动脉系统的数学模型之前，我们首先提出适当的假设，以简化模型并了解系统的机理.在这个问题中，系统是轴对称的，即动脉、组织和袖带是轴对称的，具有相同的轴(参见图1(a)).脂肪、肌肉和其他软组织虽然具有不同的力学性质，如弹性模量、泊松比等，但它们可以看作是具有相同力学性质的各向同性均匀弹性体.因此，弹性模量和泊松比保持不变.此外，忽略了骨骼和身体力量的影响.

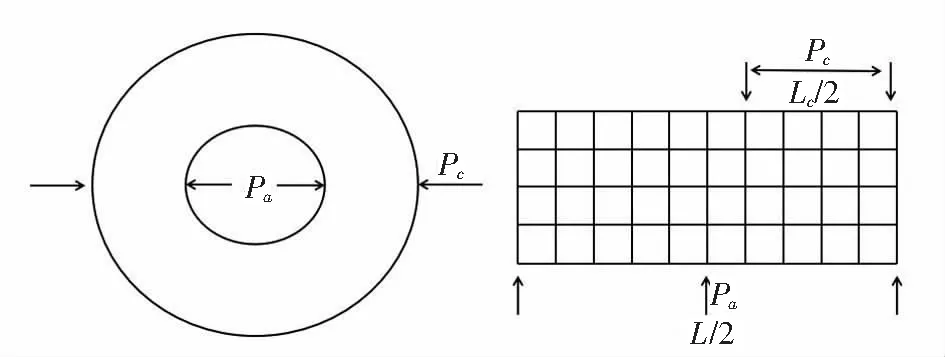
(a) (b)图1 (a)袖带-组织-动脉系统结构图；(b)计算区域Fig.1 (a)Geometry of cuff-tissue-artery system;(b)The computational region

1.1 袖带模型

在袖带充气和放气的过程中，袖带的外壁会发生轻微的变形.因此，外壁视为刚性.在袖带变形过程中，袖带内壁紧贴组织，因此认为袖带的内壁顺应性足够大.袖带压力始终与外部组织的应力相同.袖带内的空气被认为是理想气体.此外，袖带充气和放气的过程都被视为绝热过程：

(1)

式中：Pc是袖带压强；Patm是标准大气压；Vc是袖带体积；参数k=1.4，代表绝热过程；Q代表在特定时间袖带内的剩余空气量.

1.2 动脉壁模型

实验发现，动脉壁的横截面积随着血压的升高而增大，直至达到最大横截面积.然而，随着跨壁压力的增加，横截面积的膨胀先快后慢.也就是说，当动脉扩张时，随着跨壁压力的增大，动脉壁顺应性迅速降低.此外，当血管壁塌陷时，跨壁压力变小，血管顺应性也显著下降.根据这些实验结果，文献[20-22]提出了由动脉顺应性描述的动脉壁模型，见式(2).

(2)

式中：A0是跨壁压力为零时动脉的横截面积；Am是动脉的最大横截面积，参数Ca和Cb用来描述动脉力学性质.在后面的模拟中，我们使用Ca=0.09 mmHg-1,Cb=0.03 mmHg-1，该参数数值来自于论文[20-21].

1.3 组织模型

组织通常被视为弹性体，组织的变形近似为线弹性.因此，组织的变形可以用一组张量形式的弹性方程来描述，即平衡方程式(3)、几何方程式(4)和物理方程式(5).

平衡方程：

σij,j+Fi=0,

(3)

式中：σij=σji，是应力张量；Fi是体积力.

几何方程：

(4)

式中：εij=εji，是应变张量.

物理方程：

σij=Cijklεkl,

(5)

式中，Cijkl是刚度张量.

在这个问题中，组织的几何形状、外力分布和约束条件都是对称的.因此，该问题可视为空间轴对称问题.一般来说，极坐标r,θ,z比笛卡尔坐标x,y,z能更方便地解决这个问题.由于对称性，任意一点的应力、应变和位移都是独立于θ的.也就是说，它们是r和z的函数.更重要的是，为了保持对称，我们可以得到τrθ=τzθ=uθ=0.因此，对于空间轴对称问题，可以用柱坐标形式具体地写出一组弹性方程.

平衡方程：

(6)

几何方程：

(7)

物理方程：

(8)

式中：θ=εr+εθ+εz；E是弹性模量；μ是泊松比.

2 迭代算法

由于边界条件的非线性特性，直接用有限元法求解弹性方程是困难的.为了克服这一问题，提出了利用虚功原理的迭代法.

由于先前的假设忽略了物体的体积力，因此弹性体只受表面力的作用.对于具有体积τ和表面积S的弹性体，S分为力面域Sσ和位移面域Su.表面力，其分量是Xi，作用于Sσ.位移，其分量为ui，作用在Su.假定物体中存在任意的虚位移，由于Su上位移是固定的，物体表面力在Su上所做的功为零.不失一般性，可以将表面力作用的区域设置为S.因此，表面力所做功的变分是

(9)

由于变形，物体的弹性势能变分为

(10)

应力张量具有对称性，将式(7)代入式(10)，可将物体弹性势能的变分改写为

(11)

总能量变分为

(12)

由于平衡方程σij,j=0，有

(13)

利用高斯散度定理，可以得到

(14)

其中，lj是表面法方向的方向余弦.

因此，式(12)可以改写为

(15)

当弹性体处于平衡状态时，总能量最小.为了使总能量达到最小，我们选择δui=-c(Xi+σijlj),c>0来更新ui使得δE<0.

3 数值实验

在进行数值实验之前，我们预先设定了一些参数的值：E=5×104Pa,μ=0.45,Ca=0.09 mmHg-1,Cb=0.03 mmHg-1,r0=0.02 cm,rm=0.252 31 cm, 收缩压Ps=130 mmHg,舒张压Pd=70 mmHg, 袖带压强Pc=100 mmHg ，袖带外壁和内壁的半径Rm=2.7 cm，R0=2.2 cm,组织和袖带长度L=20 cm，Lc=4 cm.

由于几何结构的对称性(参见图1(a))，我们只分析了一半组织的纵切面.当使用有限元法时，我们使用正方形单元.

3.1 量纲分析

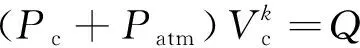
(16)

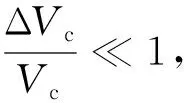
(17)

通过忽略ΔVcΔPc，式(17)可以被进一步简化为

(18)

在实际测量中，当袖带压力为100 mmHg时，袖带压力振荡幅度约为1.5 mmHg.在这种情况下，我们可以估计相对体积变化率为

(19)

ΔuR0≈6.68×10-4cm.

(20)

3.1.1 评价由式(20)可知，外部组织位移变化的数量级约为O(10-4)cm.因此，在数值计算中，网格细化所产生的数值误差应小于它.这一发现之所以如此重要，是因为在无法达到精度的情况下，数值误差会随着迭代次数的增加而扩大，这在以前的文献中被忽略了.

3.2 单元分析

实际上，在使用有限元法时，需要选择合适的单元和单元长度，以保证计算精度，减少计算时间和内存开销.在这里，我们比较两个元素，低阶单元和高阶单元.它们之间的主要区别在于高阶单元具有二次位移行为，因为两个节点之间有一个中间节点.

3.2.1 收敛阶在数值计算中，我们一直关注收敛阶.利用收敛阶可以计算出合适的单元长度.假设u*是弹性方程的真解，uh是当单元长度为h时的数值解.如果存在常数C使得|uh-u*|≅Chα成立，则称该数值方法的收敛阶为α.于是有

(21)

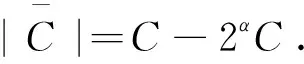
对式(21)两边取对数，有

(22)

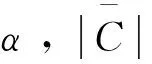
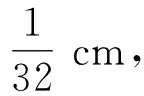
图2 (a)、(b) 舒张压和收缩压下网格细化后的外部组织位移变化；(c) 收敛阶Fig.2 (a) (b) Displacement change of external tissue by mesh refinement under diastolic and systolic pressure；(c) Convergence order

事实上，在我们的研究中，我们更关注血压变化时的袖带压力振荡或袖带容积振荡.在这里，我们研究外部组织从舒张压到收缩压的位移振荡，即外部组织的位移振幅.

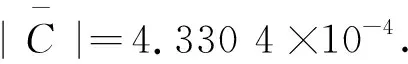
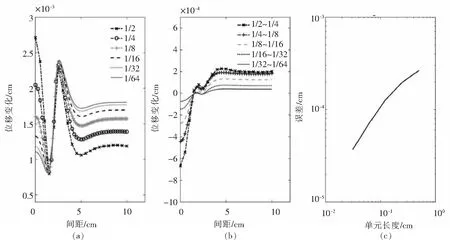
图3 (a) 不同单元长度下的外部组织位移振幅;(b) 网格细化后外部组织的位移幅度；(c) 收敛阶Fig.3 (a) Displacement amplitude of external tissue under different element lengths; (b) Displacement amplitude change of external tissue by mesh refinement；(c) Convergence order

3.2.3 高阶单元现在用高阶单元来研究特定血压下网格细化产生的位移变化.从图4(a)、(b)可以看出，当单元的长度变小时，由网格细化引起的从袖带中心到组织末端区域内的外部组织的位移变化的数量级迅速减小到O(10-4) cm，甚至更小.

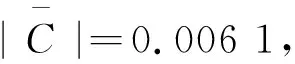
本文对参加“2018年江苏省定向锦标赛暨江苏定向邀请赛”中南京普通高校的部分学生进行随机问卷调查，共发放150份调查问卷，回收150份调查问卷，删除无效问卷25份后，有效问卷为125份。

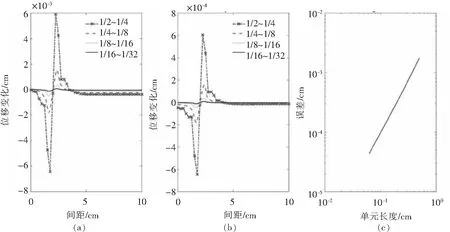
图4 (a)、(b)舒张压和收缩压下网格细化后的外部组织位移变化；(c)收敛阶Fig.4 (a)、(b) Displacement change of external tissue by mesh refinement under diastolic and systolic pressure；(c) Convergence order

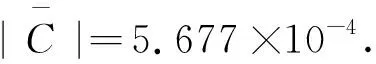
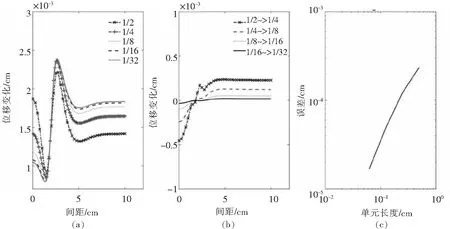
图5 (a) 不同单元长度下的外部组织位移振幅；(b) 网格细化后外部组织的位移幅度；(c) 收敛阶Fig.5 (a) Displacement amplitude of external tissue under different element lengths； (b) Displacement amplitude change of external tissue by mesh refinement；(c) Convergence order

3.2.4 评价无论是特定血压下的位移问题还是一段时间内的位移变化问题，高阶单元所需的单元长度是低阶单元的8倍以上，高阶单元的收敛阶是低阶单元的2倍左右.这些都是高阶单元的优点，我们将在后面的数值模拟中使用它们.

从表1可以看出，网格生成对于特定血压下的位移问题非常重要.需要大量的网格才能达到预期的精度.事实上，这一问题在以往的文献中并没有得到重视.然而，对于位移变化问题，有一个有趣的结果是我们只使用较大长度的单元就可以满足精度要求.实际上，我们研究的重点是袖带压力振荡.通过分析可知，在数值模拟中采用较大长度的单元能获得较高的精度和较少的计算成本.

表1 单元种类和问题种类的影响

4 理论验证

本节给出一些假设来简化模型，以相关的理论分析来验证迭代算法的准确性.由于在袖带下组织外侧的边界条件几乎保持不变，在这里对模型进行了一些简化：

1) 组织是轴对称的，无限长.

2) 平移不变性，即径向应力和位移不随纵向坐标的变化而变化.

4.1 Love函数

在1.3节中，我们给出了空间轴对称问题的平衡方程、物理方程和几何方程.因此，我们可以得到位移控制方程，如式(23)所示

(23)

(24)

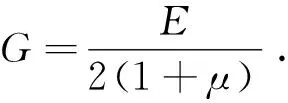
∇4φ=0.

(25)

式(25)说明φ(r,z)是双调和函数.

此外，通过将位移分量代入物理方程和几何方程，可以得到应力分量

(26)

因此，一旦知道了双调和函数是什么，就可以得到所有的位移和应力分量.

由径向位移的变量分离和平移不变性，可以假设φ=f0(r)+f1(r)z+f(z).由于∇4φ=0，可以得到

(27)

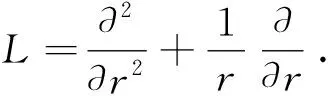
由于r和z的任意性,可以得到

(28)

因此，φ(r,z)可以写成φ=f0(r)+f1(r)z+C1z2+C2z3.于是，可以得到纵向位移

(29)

由于w|z=0=0，有2(1-μ)Lf0(r)+2C1(1-2μ)=0.因此式(29)可以改写为

(30)

同时，可以得到

(31)

由于ur,σr,σz,w独立于f0,C1，可以忽略它们的影响，令f0=0,C1=0，于是φ(r,z)可以重写为φ=f1(r)z+C2z3.

Lf1(r)=C3,

其中C3是常数.如果Lf1(r)=C3成立，则L2f1(r)=0显然也成立.

另一方面，知道应该有两个边界条件和两个未知参数C2,C3.然而，可发现，当f1有一个常数之间的差异，位移和应力分量不发生改变，因此，只需要三个条件.

由Lf1(r)=C3，可知

(32)

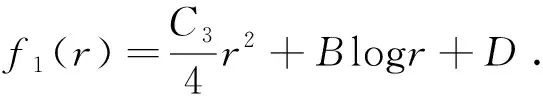
由于f1显示表达，则有

(33)

4.2 位移和应力表达式

在该问题下给出三个条件，在内部组织上给出位移边界条件，在外部组织上设置应力边界条件.此外，横截面上的纵向应力积分等于0，即

因此，我们有

(34)

4.3 理论和数值结果的比较

如前所述，只考虑位移在一段时间内的变化.因此，有必要对位移变化问题的理论结果和数值结果进行比较.

根据先前的估计，当袖带压力振荡的振幅为1.5 mmHg时，外部组织的位移变化为O(10-4) cm(见式(20)).此外，根据式(34)，可以得到外部组织的位移

进而，有

在量纲分析中，可知道ΔuR0≈6.68×10-4cm，ΔPc≈1.5 mmHg，这样就可以得到内部组织的位移变化Δu≈0.043 cm，这与数值解(≈0.04 cm)几乎是一致的.这在一定程度上说明了我们理论的正确性，这一结果也说明动脉壁变形达到O(10-2) cm或超过一定程度时，会出现明显的袖带压力振荡幅度.

5 未来展望

今后，我们将进一步对非轴对称问题进行理论分析和数值模拟.一方面，动脉和组织的几何形状不是轴对称的.另一方面，动脉在受到外力压迫时会发生塌陷，很难保持圆形.经验动脉壁模型就不再适合.因此，在非轴对称问题中有许多有趣的问题值得探讨.