基于几何精度稀释的矢量潜标最优布站

丁 超, 戴卫国,*, 王 森, 程玉胜

(1.海军潜艇学院航海观通系, 山东 青岛 266000; 2.中国人民解放军91154部队, 海南 三亚 572000)

0 引 言

矢量潜标能够获得同时共点的声压信息与多路振速信息[1-2],组阵之后,既能获得更高的信噪比,也能适用多种定位算法,因而在水声目标被动定位中具备了诸多优势。被动定位方法按照定位体制与测量类型主要可以分为以下几类:基于到达方向(direction of arrival,DOA)[3-6]、基于到达时差(time difference of arrival,TDOA)[7-10]、基于到达频差[11]、基于多普勒变化率[12]、基于相位差变化率以及联合定位方法[13-16]等。

在以上方法之中,到达频差、多普勒变化率、相位差变化率等的测量估算,需要目标与观测平台之间有较快的相对运动速度,并且需要定位系统对目标运动信息有一个较为准确的估计[17],并不适用于潜标环境。基于DOA的定位方法原理简单、易于实现,是最为常用的目标定位方法之一;基于TDOA的定位方法结果稳健、抗噪性好,对远距离目标有一定的定位能力。因此,二者成为矢量潜标阵列的常用定位方法,结合两种算法的矢量潜标阵列定位能力分析具有更好的普适性。考虑到声线弯曲、多途效应等复杂海洋信道情况,本文DOA定位与TDOA定位均在二维平面进行。

矢量潜标阵列水声目标被动定位精度受多种因素综合影响,除去海洋信道环境等外界因素干扰、声纳探测性能等硬件设备影响,在信号处理方法确定的情况下,从布阵角度分析[18-19],提高阵列定位精度的途径可以分为两类:增加阵元数量和优化布站几何。本文对矢量潜标阵列两种被动定位算法进行简要介绍,并结合具体定位算法,针对阵元数量和布站几何展开分析研究,以求获得矢量潜标阵列的最优布站。

1 定位原理及性能度量方法

定位误差大小是衡量定位系统性能的重要指标。常用的定位误差描述和度量方法有:均方误差、均方根误差、圆概率误差、克拉美罗下界以及几何精度稀释(geometrical dilution of precision, GDOP)等[20-26]。其中,GDOP是一种十分常用的定位误差评估方法[27-30],能够以等高线图形式直观形象地表示出定位系统在不同空间位置的定位误差大小,某点处值越小表示该处定位精度越高,方便对不同定位系统的性能进行比较。本文选用GDOP来对矢量潜标阵列定位能力进行度量。

1.1 DOA定位

两枚矢量潜标可以获取两个方位信息,两条非平行方位线交叉可以获取目标位置。实际情况中,阵元可能多于两个。假定声源位置T(x,y)未知,第i号阵元位置为Si(xi,yi),易得几何关系如下:

(1)

式中：θi为目标辐射噪声到达阵元Si的方位；N为阵元数量。

对式(1)进行全微分,整理可得

(2)

将式(2)整理成矩阵形式:

dD=GdT+dS

(3)

式中：dD=[dθ1,dθ2,…,dθN]T为测向误差,其中

为转移矩阵；dT=[dx,dy]T为定位误差；

为站址误差。

由伪逆法可得定位误差为

dT=(GTG)-1GT(dD-dS)=A(dD-dS)

(4)

则定位误差协方差矩阵为

PdT=E{dTdTT}=A{E[dDdDT]+E[dSdST]}AT

(5)

则DOA定位误差GDOP为

(6)

1.2 TDOA定位

三枚矢量潜标可以获取两组时延信息,每组时延信息可以确定一条双曲线,两条双曲线交汇可以获取目标位置。实际情况中,阵元可能多于3个。假定声源位置T(x,y)未知,主站位置为S0(x0,y0),第i号副站位置为Si(xi,yi),易得几何关系如下:

(7)

式中：c为海洋声速；τi为目标辐射噪声到达阵元Si的用时；N为副站数量。

水声目标被动定位中,τi无法直接获得,但其差值可以通过时延估计求得

(8)

对式(8)进行全微分,整理可得

(9)

将式(9)整理成矩阵形式:

dR=HdT+dS

(10)

式中：dR=[dΔr1,…,dΔrN]T为声程差估计误差；

为转移矩阵；dT=[dx,dy]T为定位误差；

为站址误差。

由伪逆法可得定位误差为

dT=(HTH)-1HT(dR-dS)=B(dR-dS)

(11)

则定位误差协方差矩阵为

PdT=E[dTdTT]=B{E[dRdRT]+E[dSdST]}BT

(12)

则TDOA定位误差GDOP为

(13)

2 矢量潜标阵列实际应用需求

矢量潜标阵列在实际应用中有以下需求:

(1)潜标布放海域,缺乏目标位置、航向、航速等先验知识,阵列需要具备全向探测能力;

(2)潜标阵列宜适用于多种算法,以便提高定位精度;

(3)综合考虑工程实现难度及布放成本、计算成本等问题,潜标数量不宜过多、阵列结构不宜复杂;

(4)矢量潜标阵列的主要目的在于警戒,故宜少枚多组,而非一组多枚。

阵列拓扑结构可以分为线型、面型(包括非中心型结构和中心型结构)、球型3大类,依次如图1所示。

图1 阵列拓扑结构

线型结构构造简单、信号处理简便,但其定位盲区过大,不适用于潜标环境;球型结构在海洋中布放十分困难,且系泊系统运动的不稳定性会导致定位误差增大[31],同样不适用于潜标环境。

综合以上,矢量潜标阵列宜选用呈旋转对称的面型拓扑结构,阵元数量三枚至多枚。

3 矢量潜标阵列阵元数量研究

呈旋转对称的面形拓扑结构可看作是均匀圆阵,分为无圆心均匀圆阵与有圆心均匀圆阵两类。本节将对三至八元无圆心和有圆心均匀圆阵的GDOP分布进行计算并比较分析,以确定阵元数量对定位精度的影响。不妨定义GDOP值小于500的区域为高定位精度区域,以其面积大小反映某算法下某阵列的定位精度。由于等高线图形状的不规则性,本文将GDOP图划分为足够细小的单元,使用统计法计算等高线内面积。

3.1 阵元数量对定位精度的影响

为比较阵元数量对DOA定位精度的影响,控制阵列半径、测量误差、站址误差等因素不变,比较不同阵元数量的阵列GDOP分布。

3.1.1 阵元数量对DOA定位精度的影响

设置仿真条件如下:阵列几何中心位于原点,阵列半径500 m,测向误差标准差均为0.2°,之间相关系数为0,无站址误差。以三元、四元阵为例,其DOA定位GDOP分布如图2所示,其中,红色圆点为阵元位置,4条等高线值由小至大分别为500,1 000,2 000,5 000。

图2 DOA定位GDOP

比较两种类型圆阵DOA定位的高定位精度面积,结果如图3所示。

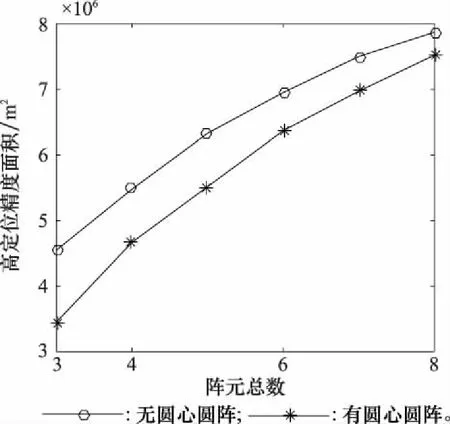
图3 阵元数量对DOA定位影响

通过对比分析,可以得到以下结论:

(1)三元有圆心均匀圆阵(即线阵)存在严重的DOA定位盲区;

(2)随着阵元数量增加,阵列DOA定位精度逐渐提高,但提高速度越来越慢,故增加阵元的性价比将随着阵元数量增多而降低。

3.1.2 阵元数量对TDOA定位精度的影响

设置仿真条件如下:阵列几何中心位于原点,阵列半径500 m,时延误差标准差均为0.03 s,之间相关系数为0,声速为1 500 m/s,无站址误差。以三元、四元阵为例,其TDOA定位GDOP分布如图4所示。其中,蓝色圆点为主站位置,红色圆点为副站位置,4条等高线值由小至大分别为5 00,10 00,2 000,5 000。

图4 TDOA定位GDOP

比较两种类型圆阵TDOA定位的高定位精度面积,结果如图5所示。

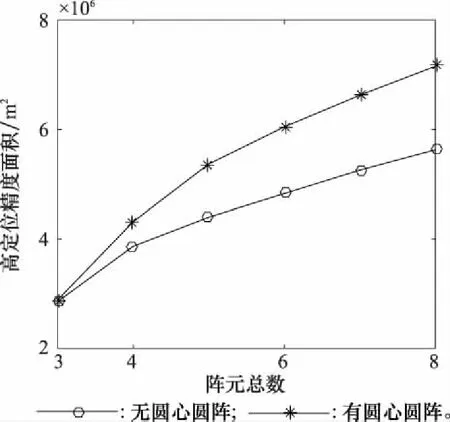
图5 阵元数量对TDOA定位的影响

通过对比分析,可以得到以下结论:

(1)三元无圆心均匀圆阵及有圆心均匀圆阵均存在严重的TDOA定位盲区;

(2)随着阵元数量增加,阵列TDOA定位精度逐渐提高,但提高速度越来越慢,故增加阵元的性价比将随着阵元数量增多而降低。

3.2 潜标阵列阵元数量选择

参与定位的阵元数目对定位精度有很大影响,阵元数目越多,获取到的待测目标信息越丰富,通过冗余信息处理所获取的目标位置也就越精确;同时,阵列定位精度与其空间结构紧密相关,阵元数目越多,阵型结构可以设计的越复杂,其全向定位能力也就相对越好。

当然,阵元数目也并非越多越有利。除去经济因素之外,首先,随着阵元数量增加,潜标阵列布放难度将急剧增加;其次,随着冗余信息增加,计算复杂度和运算量将大大增加,信息利用的充分性和定位结果的实时性将难以得到保证。

结合上文计算分析及实际使用经验,矢量潜标阵列具有以下特点:

(1)矢量潜标阵列想要兼顾DOA定位与TDOA定位,至少需要3个阵元,若考虑到潜标损坏替补等特殊情况,需要4个以上阵元;

(2)三阵元时所存在的严重的定位盲区,在四阵元以上时会被极大消除,故四阵元是矢量潜标阵列定位性能的质变点;

(3)随着阵元数量增加,阵列定位精度提升越来越少,工程实现难度及布放成本、计算成本却急速升高,故阵元数不宜过多;

(4)在满足基本需要的基础上,应减少单组潜标数量,增加潜标阵列组数,从而覆盖更大的警戒海域。

综合考虑,本文认为四阵元是潜标阵列定位性能的质变点,也是性价比的最高点,既能够应对功能需求,也较为符合工程实际,故四元旋转对称面阵是潜标阵列的较优选择。

4 矢量潜标阵列布站几何研究

除阵元数量外,布阵几何也是影响矢量潜标阵列定位精度的关键要素。被动定位方法研究最重要的目的就是减小定位误差、提高定位精度,对比不同阵型在不同阵列半径、测量误差、站址误差下的定位精度,对于阵列最优布站具有指导意义。

四元旋转对称圆阵包含非中心阵结构的四元十字阵和中心阵结构的四元Y型阵,如图2和图4中的四元阵。设置参数如下:阵列半径500 m,无站址误差。测向误差标准差均为0.2°,之间相关系数为0;时延误差标准差均为0.03 s,之间相关系数为0,声速为1 500 m/s。分别计算DOA定位算法和TDOA定位算法下的四元十字阵和四元Y型阵的GDOP分布。以GDOP值为横坐标,统计该GDOP值等高线内得面积,结果如图6所示。

图6 两种阵型定位精度对比

可以发现:① 四元十字阵有更好的DOA定位精度,四元Y型阵有更好的TDOA定位精度,但总体来说,二者相差不大;② 两种阵型、两种算法的GDOP分布中,某等高线内面积与该等高线值基本成正比,故GDOP图中某等高线内面积的变化规律即能反应定位精度的整体变化规律。

4.1 阵列半径敏感度对比

阵列半径是阵列设计的重要参数,能够直接影响到阵列的定位精度、覆盖范围等。

4.1.1 DOA定位阵列半径敏感度对比

设置仿真条件如下:测向误差标准差均为0.2°,之间相关系数为0,无站址误差。控制阵列半径从100 m增加至1 000 m,求取两阵型DOA定位的GDOP,并计算高定位精度区域面积,结果如图7和表1所示。

表1 DOA定位阵列半径敏感度

图7 DOA定位阵列半径敏感度

4.1.2 TDOA定位阵列半径敏感度对比

设置仿真条件如下:时延误差标准差均为0.03 s,之间相关系数为0,声速为1 500 m/s,无站址误差。控制阵列半径从100 m增加至1 000 m,求取两阵型TDOA定位的GDOP,并计算高定位精度区域面积,结果如图8和表2所示。

图8 TDOA定位阵列半径敏感度

表2 TDOA定位阵列半径敏感度

通过仿真对比可以发现,DOA定位方法中,两种阵型的高定位精度面积与阵列半径基本呈一次函数关系;TDOA定位方法中,两种阵型的高定位精度面积与阵列半径基本呈二次函数关系。但在半径1 000 m范围内,同算法下,两种阵型高定位精度面积相差不大。

在实际应用中,处理相关信号时,阵列中两阵元间距应小于空间相关半径。实验证明空间相关半径约为300～500λ,其中λ为信号波长[32]。考虑到通常的信号频率范围,潜标的空间相关半径不会太大,故同算法下,两种阵型定位精度相差不大。

4.2 测量误差敏感度对比

在阵型确定的情况下,测量误差会对定位结果产生很大影响,受测量误差影响小的阵型,即抗噪能力强的阵型具有更高的实用价值。

4.2.1 DOA定位测量误差敏感度对比

设置仿真条件如下:阵列半径500 m,无站址误差。控制测向误差标准差从0.1°逐渐增加到1°,之间相关系数为0,求取两阵型DOA定位的GDOP,并计算高定位精度区域面积,结果如图9和表3所示。

图9 DOA定位测量误差敏感度

表3 DOA定位测量误差敏感度

4.2.2 TDOA定位测量误差敏感度对比

设置仿真条件如下:阵列半径500 m,无站址误差。控制时延估计误差标准差从0.01 s逐渐增加到0.1 s,之间相关系数为0,声速为1 500 m/s,求取两阵型TDOA定位的GDOP,并计算高定位精度区域面积,结果如图10和表4所示。

图10 TDOA定位测量误差敏感度

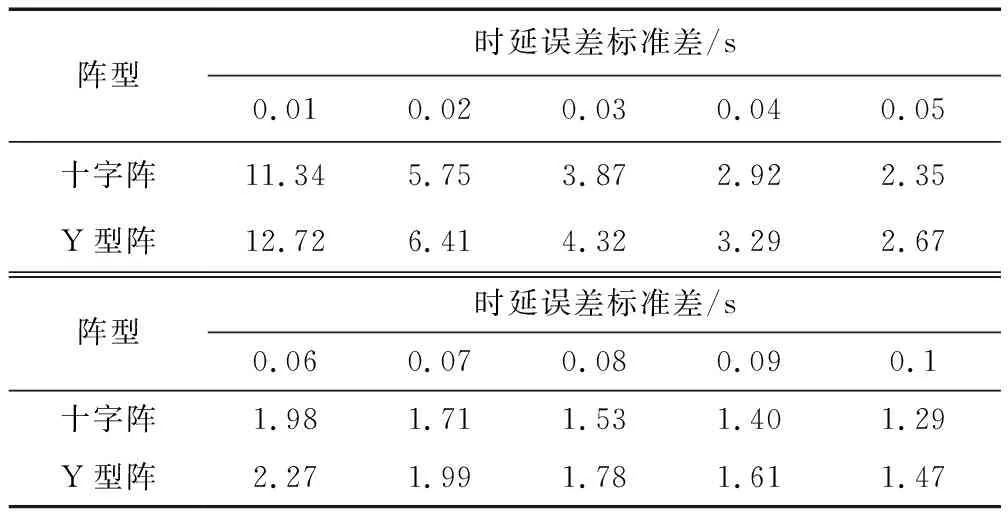
表4 TDOA定位测量误差敏感度

通过仿真对比可以发现,DOA定位方法中,四元Y型阵抗测量误差能力强于四元十字阵。随着测向误差的增加,四元Y型阵定位精度逐渐超过四元十字阵,即四元Y型阵更为可靠,更适用于复杂多变的海洋环境;TDOA定位方法中,四元Y型阵与四元十字阵的抗测量误差能力基本持平,但四元Y型阵定位精度始终优于四元十字阵。

4.3 站址误差敏感度对比

在实际应用中,站址误差不可避免,会对目标定位精度产生直接影响,抗站址误差能力强的阵型对工程实现有更好的宽容度。

4.3.1 DOA定位站址误差敏感度对比

设置仿真条件如下:阵列半径500 m,测向误差标准差均为0.2°,之间相关系数为0。控制站址误差从0 m逐渐增加到18 m,求取两阵型DOA定位的GDOP,并计算高定位精度区域面积,结果如图11和表5所示。

图11 DOA定位站址误差敏感度

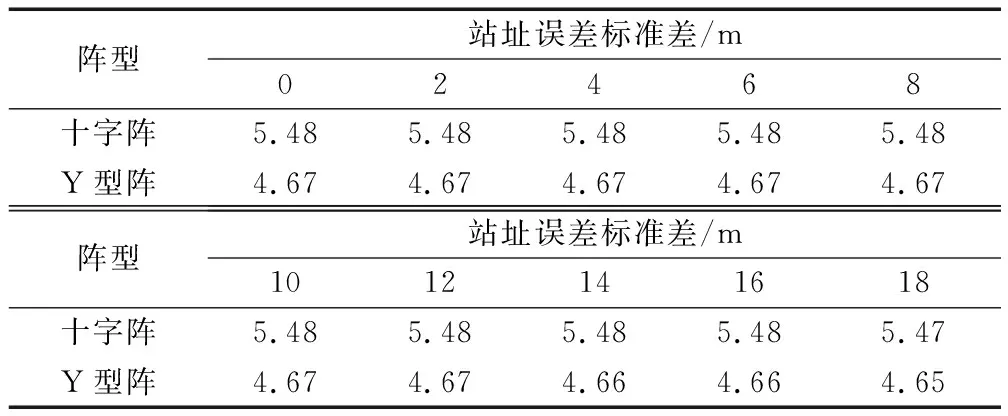
表5 DOA定位站址误差敏感度

4.3.2 TDOA定位站址误差敏感度对比

设置仿真条件如下:阵列半径500 m,时延误差标准差均为0.03 s,之间相关系数为0,声速为1 500 m/s。控制站址误差从0 m逐渐增加到18 m,求取两阵型TDOA定位的GDOP,并计算高定位精度区域面积,结果如图12和表6所示。

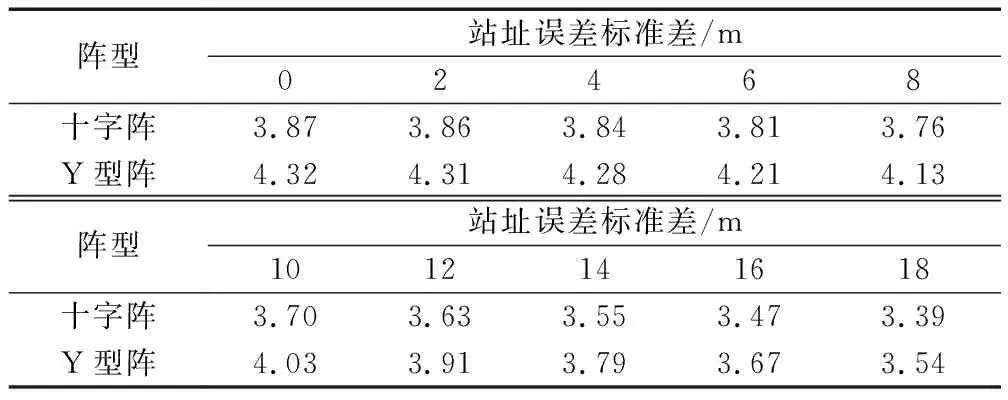
表6 TDOA定位站址误差敏感度

图12 TDOA定位站址误差敏感度

通过仿真对比可以发现,DOA定位方法抗站址误差能力较强,且在DOA定位方法中,两阵型抗站址误差能力基本持平;TDOA定位方法抗站址误差能力相对较弱,在TDOA定位方法中,四元Y型阵抗站址误差能力略逊于四元十字阵。

4.4 相关半径约束下阵列最大半径对比

在相关半径约束下,保证所有副站都在主站相关半径内时,不同阵列结构所能获得的最大阵列半径亦不相同。具体到四元十字阵和四元Y型阵,当相关半径为R时,在保证所有副站都在主站相关半径内时,四元十字阵最大阵列半径为R/2,四元Y型阵最大阵列半径为R。

设置仿真条件如下:测向误差标准差均为0.2°,之间相关系数为0;时延误差标准差均为0.03 s,之间相关系数为0,声速为1 500 m/s,无站址误差。控制相关半径从200 m增加至1 000 m,求取两阵型的最大阵列半径,并求取最大阵列半径下DOA定位和TDOA定位的GDOP高定位精度区域面积,结果如图13和图14所示。

图13 相关半径约束下DOA定位精度对比

图14 相关半径约束下TDOA定位精度对比

通过计算对比可以发现,相同相关半径约束下取最大阵列半径时,四元Y型阵的DOA定位精度和TDOA定位精度均远高于四元十字阵,且相关半径越大差距越大。

4.5 阵元覆盖面积对比

前文可知,DOA定位至少需要两个阵元,TDOA定位至少需要3个阵元,当具备4个阵元以上时,阵列定位性能将得到较大提高,且可辅助消除定位模糊。也就是说,阵元覆盖范围直接决定了阵列的有效作用范围。假定潜标阵列半径500 m,潜标有效探测范围半径5 000 m,可以求得阵列的三阵元覆盖范围及四阵元覆盖范围,如图15所示。

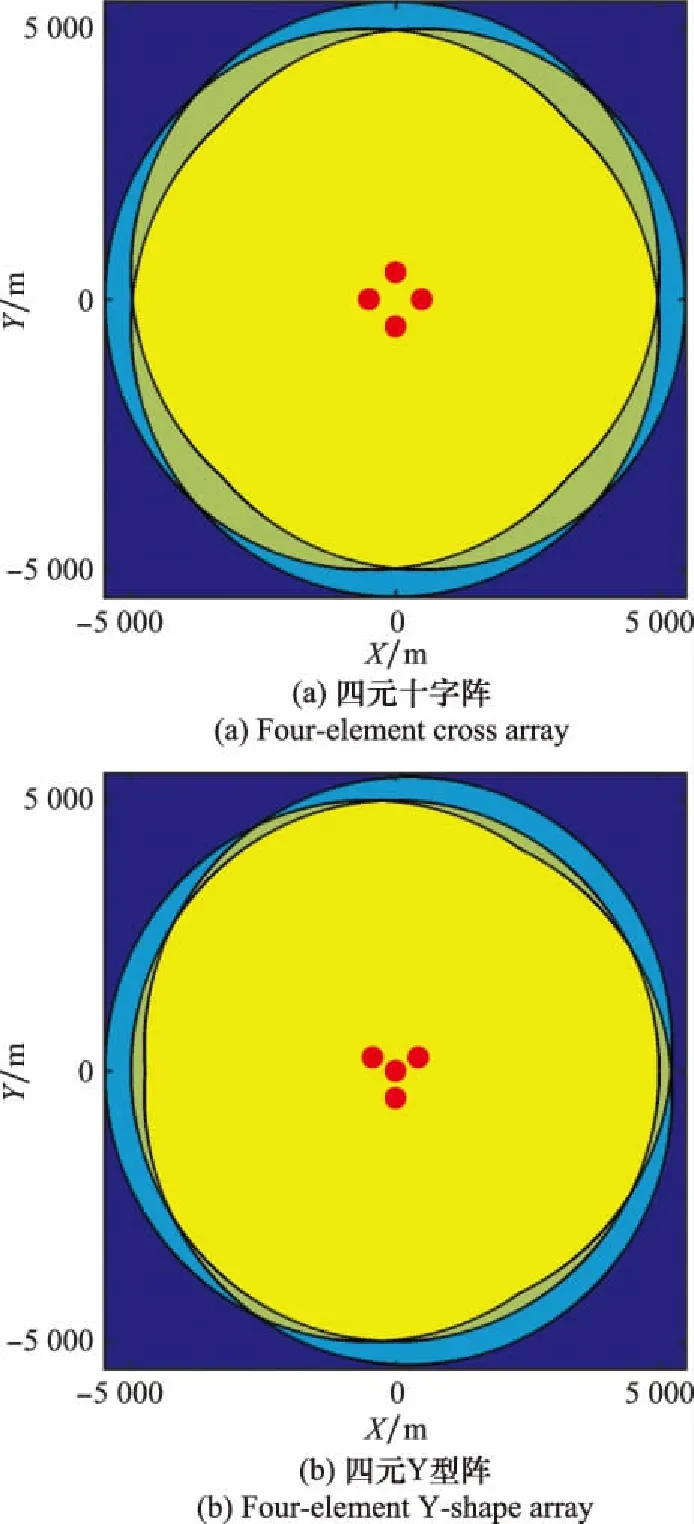
图15 阵元覆盖范围示意图

图15中,红点表示阵元位置,颜色越亮的区域覆盖阵元越多,明黄色为四阵元覆盖区,暗黄色为三阵元覆盖区。不同阵列半径下,三阵元及四阵元的覆盖面积,如图16所示。通过计算对比可以发现,相同阵列半径时,四元Y型阵的三阵元覆盖面积及四阵元覆盖面积均大于四元十字阵,且随着阵列半径增加,差距越来越大。

图16 阵元覆盖范围对比

4.6 矢量潜标阵列布站几何选择

通过对四元十字阵和四元Y型阵阵列半径敏感度、测量误差敏感度、站址误差敏感度、阵元覆盖面积等的全面对比,可以得出以下结论:

(1)同条件下,四元十字阵的DOA定位精度略高于四元Y型阵,四元Y型阵的TDOA定位精度略高于四元十字阵;

但由于DOA定位性能会随目标距离增加急剧下降,在实际应用中通常作为辅助定位方法,而将TDOA定位方法作为主要定位手段,故四元Y型阵更具实用性;

(2)同条件下,四元Y型阵具有更好的抗测向误差能力,因为能够更好地应对复杂的海洋环境;

(3)同条件下,DOA定位时两种阵型抗站址误差能力基本持平;TDOA定位时四元Y型阵抗站址误差能力略逊于四元十字阵,但在实际情况下,Y型阵的TDOA定位能力仍强于十字阵;

(4)相同相关半径约束下取最大阵列半径时,四元Y型阵的DOA定位精度和TDOA定位精度均远高于四元十字阵;

(5)相同阵列半径时,四元Y型阵的三阵元及四阵元覆盖面积均大于四元十字阵;

(6)就两种阵型的GDOP图等高线形状而言,四元Y型阵无论DOA定位还是TDOA定位,各方位定位能力均较均衡;而四元十字阵在TDOA定位时各方位定位能力存在严重的不均衡性。

综合考虑,本文认为四元Y型阵具有更稳健的定位性能,更适合于矢量潜标阵列的实际应用环境。

5 结 论

除海洋环境和潜标性能外,阵元数量和布站几何是影响矢量潜标阵列定位精度的关键要素。结合实际需求,通过理论推导及仿真证明,本文得出以下结论:

(1)旋转对称面阵具备较好的全向探测能力,且便于在复杂海洋环境下工程实现,在几种阵型中最能够满足潜标阵列的警戒需求;

(2)四元潜标阵列极大消除了三元潜标阵列的定位盲区,是潜标阵列定位能力的质变点,也是性价比的最高点,考虑到警戒声纳宜少枚多组以扩大覆盖海域的需求特点,四元阵列是矢量潜标阵列的最优选择;

(3)四元旋转对称面阵包含四元十字阵及四元Y型阵两种,其中,四元Y型阵在同等条件下,具备更高的TDOA定位精度、更高的抗测量误差能力、更大的有效作用范围,同时抗站址误差能力也没有短板,更加适用于矢量潜标阵列。

综合考虑,成旋转对称的四元Y型阵是基于GDOP衡量标准的矢量潜标阵列的最优布站。