基于神经网络和模型迁移学习的不相关多源频域载荷识别

陈德蕾，王 成+，曾 煜，李海波，赖雄鸣,陈叶旺

(1.华侨大学 计算机科学与技术学院，福建 厦门 361021；2.厦门市企业互操作与商务智能工程技术研究中心,福建 厦门 361021；3.华侨大学 机电及自动化学院，福建 厦门 361021)

0 引言

动态载荷识别技术[1]在现代工程设计、可靠性试验、振动控制等方面广泛应用。在工程实践中，振动幅频特性或振动响应相对容易测量，而因为施加的力的作用即载荷激励通常无法轻易得到，所以在某些条件下，如飞行中的导弹、海上平台和受激励情况影响的其他大型建筑物，激励和振动系统的参量不易直接测出，往往需通过逆分析才能获取相应参数，如获取系统载荷。载荷识别属于第二类反问题，主要根据已知的一些系统特性来获得载荷。对于载荷识别问题,由于识别过程的复杂性以及各种因素,如结构系统的频率域、测量精度、激励类别等都会影响载荷识别效果，因此确定随机动载荷并科学地制定相应的载荷谱是工程设计中亟待解决的问题。

所谓反问题指的是通过一些观测特征来求解内部规律的问题[1]。在载荷识别中，需要通过实验测得的响应数据来反求未知载荷，因此求解反问题的方法通常被用来识别作用在工程结构上的荷载[2]。载荷识别方法从方法域上可分为频域法和时域法，频域方法主要通过激励与响应之间的传递函数的逆运算来实现。JOHN等[3]基于传递函数直接求逆法对载荷位置未知情况下的动态载荷进行识别，并利用奇异值分解技术进行矩阵求逆。然而，进行逆运算的过程中通常需要求解矩阵的广义逆，并且经常遇到系数矩阵求解和奇异值分解问题的不适定问题[4-5]。为克服逆频率传递函数中固有频率附近存在的不适定问题，姜金辉等[6]提出一种基于矩阵谱分解理想的多源相关随机载荷识别方法，利用正则化算法并通过L曲线法设置正则化参数，提高载荷识别结果的准确性;WANG[7]利用多个载荷源的不相关解耦频域载荷识别方程，提出一种基于频域最小二乘的不相关多源载荷识别方法，使用广义矩阵逆方法的最小二乘法将多目标优化问题转化为单目标优化问题;LIU等[8]提出一种基于盖根堡多项式展开理论及正则化的随机结构动力荷载识别方法，通过盖根堡多项式展开理论将随机结构的荷载识别问题转化为等效确定性系统，并采用改进的正则化算子克服了载荷识别问题的不适定性。针对实际工程中由测量误差产生的噪声引起的不适定问题，CHEN等[9]提出一种基于截断广义奇异值分解法的桥面响应动载荷识别方法，该方法旨在得到一个可接受的解，并使噪声对不适定问题的扰动不敏感;JIA等[10]提出一种基于加权总体最小二乘来识别随机动态载荷，该方法通过加权全最小二乘法来减小噪声的影响，提高随机动态载荷识别的精度。为克服谐振频率下不相关多源频域载荷识别的经典最小二乘广义方法的不适定逆问题，WANG等[11]提出一种基于改进Tikhonov正则化算子的正则化方法,该方法不需要大量的实验数据用于训练，且与神经网络相比需要的参数数量更少，运行时间更短;WANG等[12]提出一种基于新型分数阶Tikhonov正则化的载荷识别方法，通过将原问题变成无约束优化问题，并利用超记忆梯度法进行求解;CHEN等[13]提出一种基于预处理最小二乘QR分解法的动载荷识别方法，该方法对不适定问题具有较强的鲁棒性，比传统的时域方法具有更高的识别精度。神经网络在解决回归问题上有很好的效果，因此在载荷识别方面也有相关研究，CAO等[14]提出使用BP神经网络建立动载荷和响应之间的关系模型，但是该模型容易陷入局部最优，需要取得一个较好的神经网络初始权重才能得到较好的结果;WANG等[15]提出一种基于多神经网络和证据理论的载荷识别方法，综合两种数据融合方法的优点和缺点，结合振动数据、电流数据和液压缸数据，实时获取掘进机的动载荷;王珲玮等[16]提出一种基于遗传算法优化BP神经网络的弹体结构载荷识别方法，该方法可以有效解决BP神经网络易陷入局部最优解的问题，且具有更快的收敛速度和更高的识别精度;ZHOU等[17]提出一种利用深度递归神经网络(Recurrent Neural Network, RNN)对非线性结构载荷进行识别的新方法，该方法即使在冲击位置未知的情况下，也具有识别复杂冲击载荷的能力，同时该模型识别精度对超参数和传感器的放置方案均不敏感。

随着深度学习的广泛应用，更多更深的神经网络框架被提出。这些深度学习框架能够有效提升模型在数据上的表现，但要建立在花费更多时间和计算资源的基础上，因此基于神经网络和迁移学习框架应运而生。考虑到某些数据或任务是相关的，迁移学习可以通过将相关任务模型的参数共享给目标任务模型来加速和优化模型训练，而不用像大多数网络那样从头开始训练。为了从不同分布的数据中训练出高质量的分类器，DAI等[18]提出一种基于实例的TrAdaBoost转移学习算法，该算法利用训练数据从不同分布的数据中选择有用的部分，以降低分类错误率。为解决迁移学习中的领域自适应问题，LONG等[19]提出了深度自适应网络，将深度卷积神经网络扩展到领域自适应；CAO等[20]提出了基于选择性对抗网络(Selective Adversarial Networks, SAN)的部分迁移学习，它只传输源域中与目标域相关的部分样本，然后通过SAN处理部分迁移学习问题，由于对抗性网络能够很好地学习领域不变性特征，在迁移学习中具有重要的作用;PANAREDA等[21]提出了开放集域自适应方法，它们利用源域和目标域之间的关系来标记目标域的样本，并将源域转换为与目标域相同的空间，最后对目标域的样本进行分类。

基于以上研究，为了解决使用神经网络进行载荷识别存在的训练效率低时间长、低精度的问题，本文提出基于神经网络和模型迁移学习的不相关多源频域载荷识别方法。对比直接使用神经网络进行训练，通过迁移学习得到的神经网络多源载荷识别模型能够得到较好的神经网络模型的初始权重，有效减少训练时间，且识别精度更高。

1 方法介绍

1.1 线性系统不相关多源频域载荷识别的理论基础

在多激励和多响应系统中，通过激励可以得到线性时不变系统的振动响应数据，即将系统的多源载荷作为输入，响应作为输出[7]，并且可以利用传递函数对系统进行求解，如图1所示。

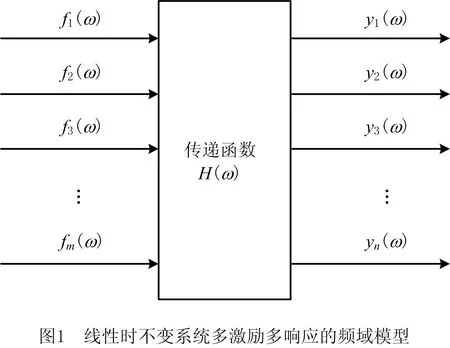
在该模型中,频率ω下m个不相关多源载荷[f1(ω),f2(ω),…,fi(ω)…,fm(ω)]作为输入，n个系统的响应数据[y1(ω),y2(ω),…,yj(ω)…,yn(ω)]作为输出,响应与不相关多源载荷的关系如式(1)所示：

(1)

式中：ω表示频率;Syjyj(ω)表示响应点yj(j=1,2,…,n1)的自功率谱;Sfifi(ω)表示不相关多源载荷fi(ω)(i=1,2,…,m)的自功率谱;|Hj,i(ω)|表示对应着载荷fi(ω)到响应yj(ω)在对应频率处的传递函数的模。

记

B(ω)=

则式(1)可以表示为：

(2)

在n≥m的情况下，通过最小二乘广义逆法可以得到不相关多源载荷的自功率谱的估计为：

(3)

由式(3)可知，多点振动响应的自功率谱与不相关多源载荷的自功率谱之间存在线性关系，因此可以利用它们之间的传递函数和最小二乘广义逆法进行求解。

1.2 基于多输入多输出神经网络的不相关多源频域载荷识别及其存在的问题

式(1)中的系统频域传递函数Hj,i(ω)i=1,2,…,m,j=1,2,…,n难以获取的情况下，可以采用数据驱动和多重多元回归分析的方法对系统输入的振动响应进行回归分析，从而得到系统的不相关多源频域载荷。

由于前馈型(Back Propagation, BP)神经网络在理论上可以拟合任何闭区间的连续函数[22]，在现有的很多回归预测问题中得到广泛的应用。多输入多输出神经网络模型是多重多元回归预测模型的一种实现，为每个频率点单独建立一个神经网络，利用多点振动响应数据作为神经网络的输入，不相关多源载荷作为神经网络的输出，并利用历史数据对网络进行训练，利用实测载荷与网络输出的误差来更新网络权值。神经网络模型训练结束后，利用测试集进行测试，进而对模型进行精度评价。

由于不相关多源频域载荷识别中存在多个频率点，需要为每个频率点建立一个多输入多输出的神经网络模型，用于该频率点的不相关多源频域载荷识别。如果每个频率点的多输入多输出的神经网络模型是独立训练的，会造成模型训练效率大大降低。而且在小样本训练数据集的实验中，神经网络模型往往表现不佳。

1.3 基于多输入多输出神经网络和模型迁移学习的不相关多源频域载荷识别

由于神经网络模型的上述问题，在载荷识别的神经网络模型中引入模型迁移学习，提升训练效率。迁移学习大致可以分为基于样本迁移、特征迁移、模型迁移、关系迁移4种方法[23]。目前，基于模型的迁移学习方法大部分是与深度神经网络进行结合，通过对现有的一些神经网络的参数或结构进行微调，并加入与目标域相适应的更改使网络能够与目标任务适配，最后对网络进行训练。比较著名的基于ImageNet的图片分类任务[24]，可以根据Google训练好的Inception_v3深度学习模型迁移到自己的图片分类任务中，用目标任务的少量数据进行Fine-tuning,训练出自己的模型。

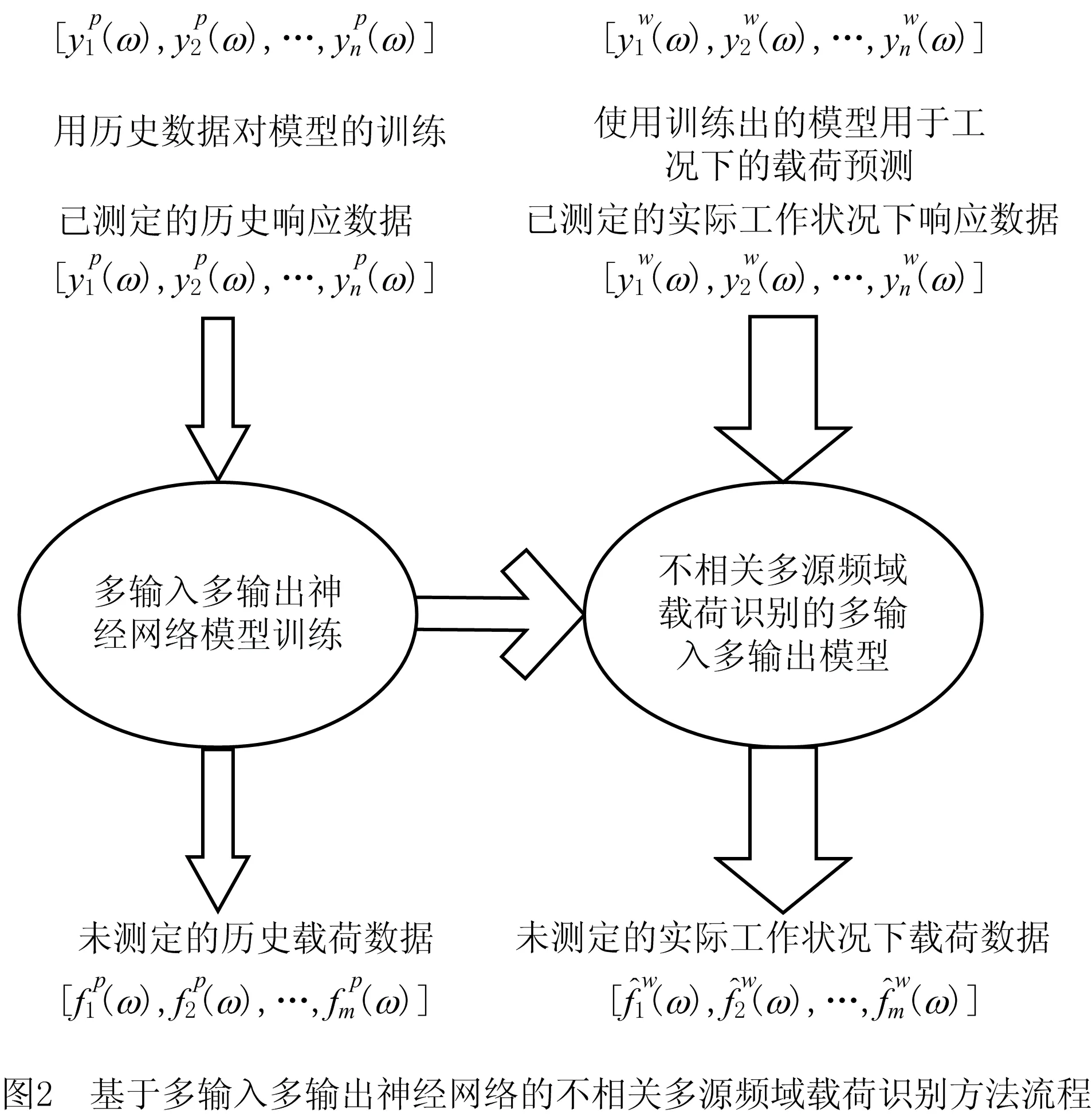
虽然不同频率的样本特征空间相同，并且识别任务均为频域不相关载荷识别，但是不同频率下的数据概率分布存在差异，而这种差异导致无法对不同频率的模型直接进行重用。但它们之间的概率分布存在一定的重叠，说明相邻频率点的载荷与响应之间的关系存在一定的相似性，使得迁移学习的引入成为可能。与本文研究相类似的研究如SHI等[25]用不同物体的目标识别任务的数据集进行迁移学习；DING等[26]将中波红外的数据知识迁移到长波红外的模型中；LISANTI等[27]提取单人图像中的知识，并将图像中的知识迁移到多人图像的任务中。因此，本研究在载荷识别的神经网络模型中引入迁移学习，对不同模型进行重用，进而提升训练效率。本文主要利用基于模型的迁移学习方法，在将辅助频率下的神经网络载荷识别模型训练好的基础上，将辅助频率的神经网络模型网络权值参数迁移到目标频率的神经网络模型中作为初值权重，然后用目标函数的数据对神经网络进行微调，达到模型迁移的目的。基于神经网络和模型迁移学习的不相关多源频域载荷识别模型如图3所示。

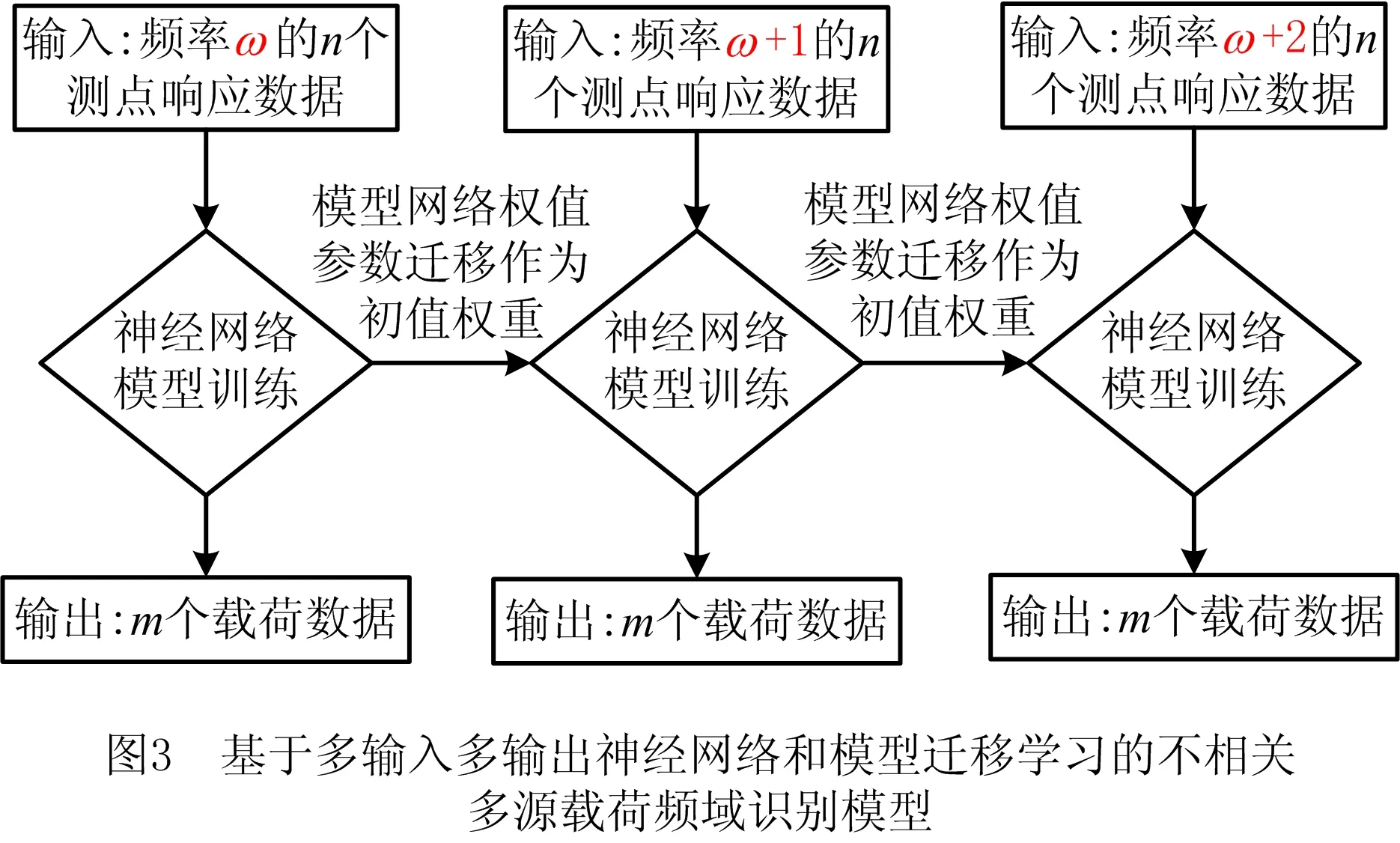
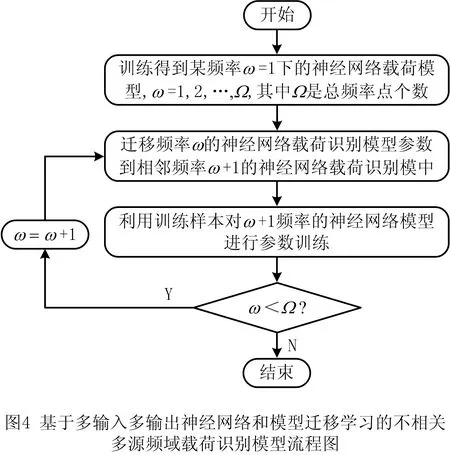
基于多输入多输出神经网络和模型迁移学习的不相关多源频域载荷识别模型的流程如图4所示，训练步骤如下：

步骤1在频率点ω=1建立一个多输入多输出神经网络模型，利用历史多点振动响应多源载荷数据对该神经网络模型进行训练，建立该频率点下的神经网络多源载荷预测模型。

步骤2为避免神经网络从头开始训练，通过迁移学习迁移该频域下已经训练好的神经网络模型参数到相邻ω+1频率的神经网络中。

步骤3利用相邻ω+1频率的历史数据对从步骤2得到的神经网络模型参数进行微调训练，从而得到相邻频率的神经网络载荷识别模型。

步骤4判断ω<Ω,即判断所有频率的神经网络载荷识别模型是否都已经建立完成，建立完成则结束；否则ω=ω+1，转步骤2。

2 实验验证结果与分析

为了验证模型迁移学习对基于多输入多输出神经网络的不相关多源载荷识别模型的有效性，本文将未加入模型迁移学习的神经网络的多源载荷识别模型与加入模型迁移学习的神经网络多源载荷识别模型进行对比，并在精度上与传统多元一次线性回归模型及最小二乘广义逆和传递函数多源载荷识别模型进行对比。

2.1 实验装置和数据集及其预处理介绍

本文的实验装置是固定在振动台上并悬挂在弹性橡皮绳上的圆柱形结构[28]。在圆柱壳的内部与外部分别存在一个球形噪声激励装置和一个悬挂式振动激励装置，其中振动激励装置包括记录振动激励、记录外部声激励和记录内部装置振动响应的传感器。内部的声激励和外部的振动激励分别有3个量级和5个量级，因此本实验共能收集到P=15组多源载荷联合激励数据。本文有两个激励源，因此载荷的预测输出m=2个。在圆柱壳上共有n=18个响应测点，其位置分布如图5和图6所示。

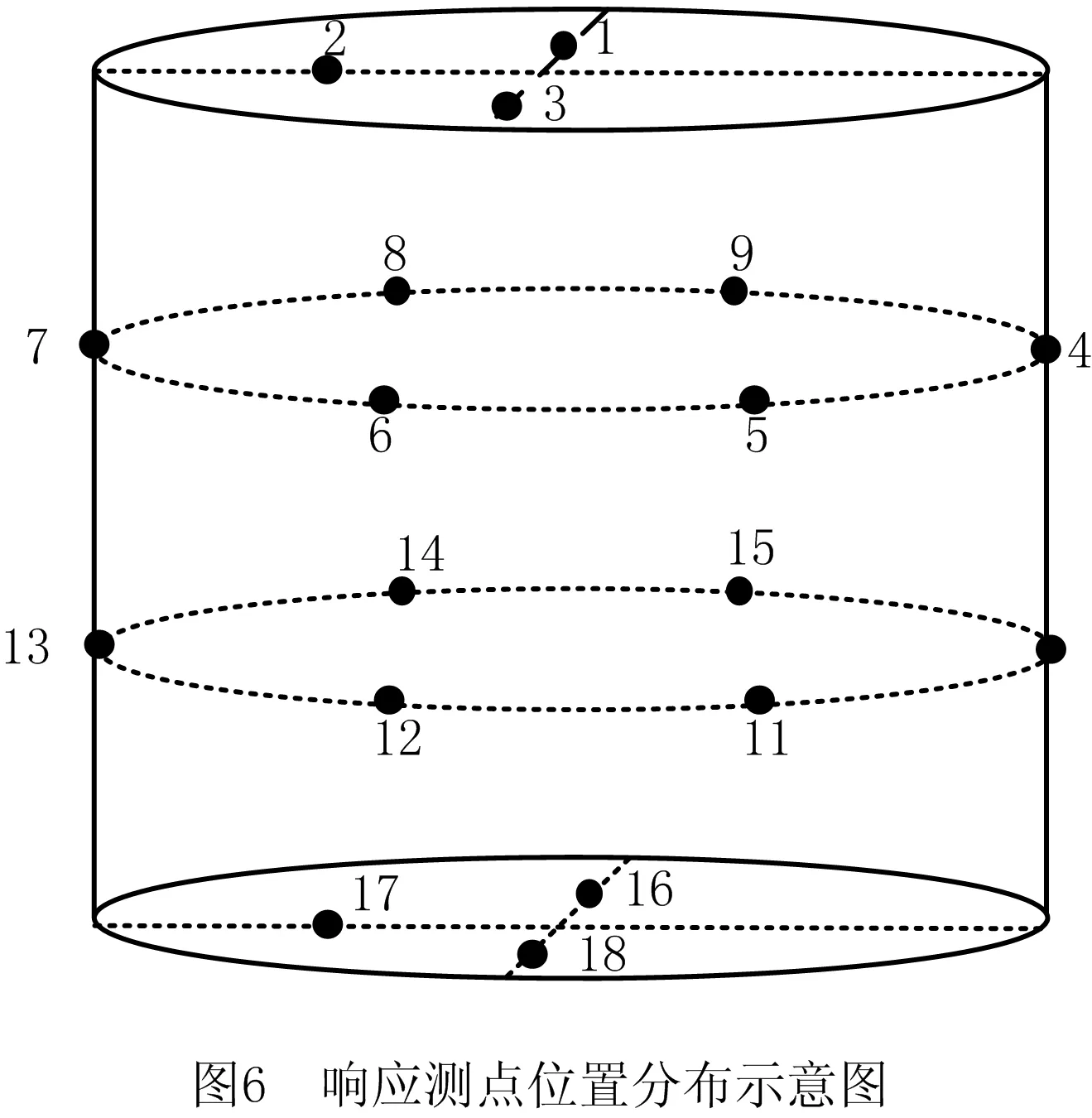
本文采集到的数据为时域的振动响应数据，因此需要通过快速傅里叶变换将时域数据转换到频域数据。变换后得到0 Hz～6 400 Hz、频率间隔为4 Hz的Ω=1 601个频率点数据。

由于不同频域下其载荷数据的数量级差距较大，会对神经网络计算损失时产生数量级的偏差。如第一个载荷真实值为2×10e-4，其预测值为2×10e-3，MAE值为1.8×10e-3，另一个载荷真实值为2×10e-3，其预测值为3×10e-3，MAE值为10e-3。虽然在误差计算时两个载荷的误差数量级相同、相差不多，但从工程上来说，第一个载荷的误差是不能满足工程上的需求的。因此，本文将载荷数据通过对数变换式(4)，使不同数量级的载荷数据变换在同一个数量级下,从而降低相对误差。

fnew(ω)=log10f(ω)。

(4)

2.2 实验评价方法与指标

2.2.1 实验评价方法

本文采用留一交叉验证法对实验结果进行验证。留一交叉验证法每次取1组作为测试集，其余14组作为训练集，直到所有组均作为过测试集。最后取所有结果的平均值作为模型度量的估计。

2.2.2 实验评价指标

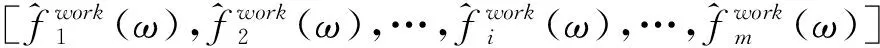
(5)

对于每一个频率ω，若预测的载荷和真实的载荷不满足式(5)，则该载荷标记为该频率下的3 dB误差载荷，所有不满足标准的载荷数据与所有预测载荷的比值即为该模型的3 dB超差率。

2.3 实验参数设置

神经网络的超参数较多，且往往决定了模型结果的好坏。因此，超参数的设定至关重要。本文采用的神经网络结构包含1个输入层、1个输出层、3个隐藏层，分别为128，64，64个全连接神经单元，如图7所示。

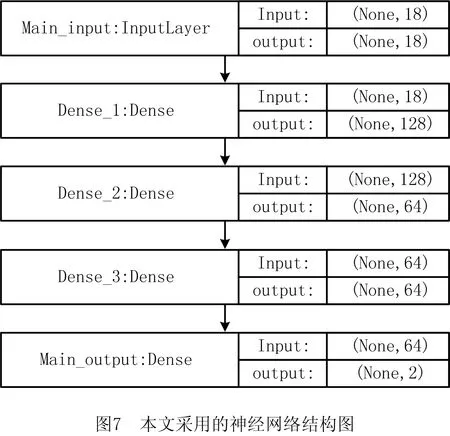
由于是对线性系统进行预测，在本文中隐藏层选用非线性拟合能力较弱的Relu作为激活函数。Relu公式如下：

(6)

式中：g(·)为激活函数;x为激活函数输入值。

误差函数选用对异常点较不敏感的平均绝对误差(MAE)。MAE公式如下：

(7)

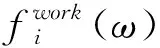
mt=β1mt-1+(1-β1)gt,

(8)

2.4 实验结果

在相同网络超参数但不同训练轮数(迁移学习+神经网络：20轮；神经网络：50轮)的条件下，基于神经网络的多源载荷识别模型与加入迁移学习的神经网络多源载荷识别模型以及最小二乘的多源载荷识别模型在3 dB误差和在训练时间上的对比如表1所示；在频率ω=4 Hz下，神经网络的多源载荷识别模型与加入迁移学习后的神经网络的多源载荷识别模型的前50轮学习效率比较如图8所示(原始神经网络模型在最低损失0.233 2在第48轮取得,加入迁移学习后最低损失0.228 9在第11轮取得)；在相同网络超参数与相同训练轮数20的条件下，基于神经网络的多源载荷识别模型与加入迁移学习的神经网络多源载荷识别模型的3 dB误差对比如表2所示。为了更直观地表示载荷识别的效果，图9所示为第8组预测载荷和实际载荷的对比图，图10所示为第8组预测载荷和实际载荷的3 dB超差图。

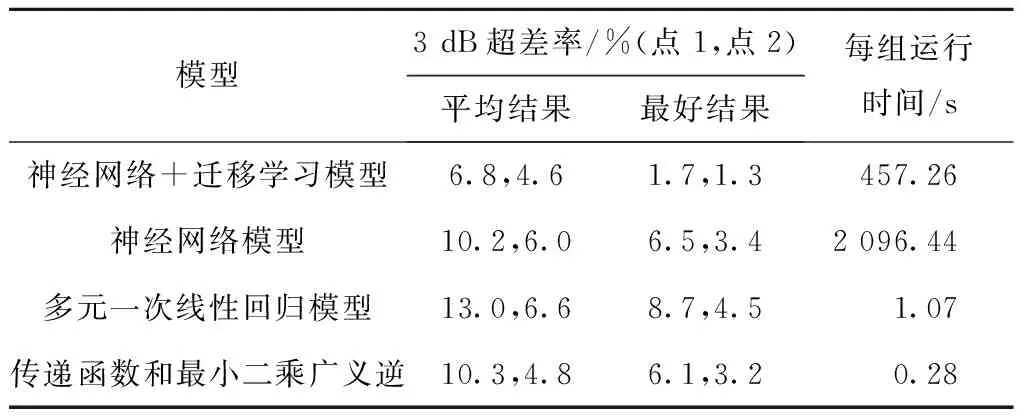
表1 基于神经网络和迁移学习载荷识别模型与基于神经网络的载荷识别模型及其他传统载荷识别方法的对比表

表2 基于神经网络的载荷识别模型与加入迁移学习的神经网络载荷识别模型的对比表

2.5 实验结果分析

从表1可以发现，单纯的神经网络模型较传统模型在本实验的小样本数据的表现并不理想，且由于神经网络中网络参数多，导致每次训练调整网络参数均会花费大量时间，远远不如多元一次线性回归模型和传递函数和最小二乘广义逆模型的训练效率。但是在相同的网络超参数(除训练轮数)情况下，加入迁移学习的载荷识别的神经网络模型可以在保证精度的基础上大大缩短训练时间，从每组2096.44 s的训练时间提升到每组457.26 s的训练时间，但由于神经网络的性质，即使在加入迁移学习后，神经网络的训练效率仍不如多元一次线性回归模型和利用传递函数的最小二乘广义逆模型。

由表1可知，不论是从平均误差结果还是最好误差结果上看，神经网络+迁移学习的模型同单纯的神经网络模型、传递函数和最小二乘广义逆模型及多元一次线性回归模型相比较，其3 dB超差率也相对较低。因为基于神经网络的载荷识别模型中不存在矩阵求逆，所以不存在传统的传递函数和最小二乘广义逆模型、多元一次线性回归模型的不适定性问题[7,11]，但是单纯的神经网络模型在本实验的小样本数据的精度并不理想，而迁移学习的加入缓解了小样本问题，大大提升了神经网络载荷识别模型的精度。

由图8可以发现，加入迁移学习的神经网络的多源载荷识别模型的训练初始误差0.95左右，神经网络的多源载荷识别模型的训练初始误差在2.4左右，说明加入迁移学习的神经网络模型权重的初值较好，也从侧面反映了迁移学习对于神经网络的多源载荷识别模型的有效性；而且加入迁移学习的神经网络的多源载荷识别模型在第5轮训练的时候收敛到比较好的误差，神经网络的多源载荷识别模型在21轮训练的时候收敛到比较好的误差，可以发现加入迁移学习的神经网络的多源载荷识别模型收敛速度明显快于神经网络的多源载荷识别模型，而且在前50轮训练内可以以更低的训练轮数达到更高的精度。并且从表2可以发现，在相同网络超参数及训练轮数的情况下，加入迁移学习的神经网络的多源载荷识别模型的预测指标也远远超过未加入迁移学习的神经网络的多源载荷识别模型。

由图9和图10以及表1可以看出，基于迁移学习的多输入多输出神经网络的不相关多源载荷识别模型在3 dB超差率的指标上平均达到6.8%,4.6%的精度，预测载荷与实际载荷十分接近，基本符合工程要求。

综合上述分析，迁移学习能够取得较好的神经网络模型的初值权重，显著提高基于多输入多输出神经网络的不相关多源载荷识别模型的训练效率，提升模型精度，且该模型能够满足工程上的需求。

3 结束语

本文针对基于神经网络的多源载荷识别模型训练效率低、时间长和精度低的问题，利用频域下相邻频率间关系相似的特点，提出了基于神经网络和模型迁移学习的多源载荷识别模型，并通过实验验证了该算法的有效性。该算法能够取得较好的神经网络模型的初值权重，有效提高训练效率，提升实验精度。在算例中，对比基于神经网络的多源载荷识别模型，基于神经网络和迁移学习的多源载荷识别模型的训练效率提升了5倍；而且基于神经网络和迁移学习的多源载荷识别模型中两个载荷的3 dB识别超差率最低能达到1.7%,1.3%远远优于传递函数和最小二乘广义逆的多源载荷识别模型的6.1%,3.2%；神经网络模型结果的好坏往往取决于神经网络权重初值的设定，加入迁移学习，可以使神经网络模型的权重初值均在一个较好的范围，从而有效提高识别精度。但基于神经网络和迁移学习的多源载荷识别模型仍然存在以下问题：

(1)神经网络的超参数较多，较难寻找到好的超参数；

(2)神经网络模型的结果存在不确定性，容易波动；

(3)神经网络模型的训练效率同一些线性回归模型相比仍然差距较大。

另外，本文实验验证采用的是线性系统，没有充分发挥神经网络对非线性函数拟合的能力，因此需要进一步在强非线性系统上进行验证。