基于数据挖掘的异常财务数据识别方法研究

金恒，过文俊

（西安航空职业技术学院，陕西西安710089）

随着我国经济的发展，上市公司的数量不断增多，上市公司提供的财务会计信息是市场参与者进行投资决策的重要依据。但近年来，上市公司进行财务数据舞弊的行为屡见不鲜。这对市场和投资者均造成了极大的伤害，破坏了资本市场公平、公正的原则。从市场和投资者的角度出发，如何识别异常的财务数据，及时发现公司的舞弊行为具有重要意义[1-7]。

对于异常财务数据的识别通常包含两种模式：一种是基于基础财务知识的统计识别模式，该模式在经济学理论的基础上对公司进行财务审计，这种方法更注重于财务模型的精确性和共性，而忽略了公司的个性；另一种是基于数据挖掘思想的数据分析方法，该模式更注重对于财务数据本身的取样和特征的提取，侧重于数据的实验。该文基于数据挖掘的模型，进行了财务数据的分析。在模型的构建上，为了解决上市公司成立时间不同导致数据格式在时间粒度累计的差异性，和由此引发的数据挖掘模型实用性差的问题，采用动态时间规整算法计算时间序列的相似度，对K 邻近算法的输入样本进行了格式统一。仿真结果表明，文中提出的基于DTW算法的异常财务数据模型，具有较朴素贝叶斯算法更高的识别精度[8-15]。

1 模型设计

1.1 动态时间规整算法

对于财务数据的处理和分析需要依托于公司的财务数据，由于公司的成立时间不同，不同公司间财务数据的采集时间粒度不同。这导致了数据格式在时间维度上的累积不同，时间跨度无法做到统一。一般的数据挖掘模型难以在该场景下发挥自身的性能，因此该文引入动态时间规整算法（DTW）进行财务数据的处理与分析。其基本原理如下：

设测试数据集为R，训练数据集为T，各个数据集样本的维度分别是m和n。对于监督性学习算法，需要比对测试数据集和训练数据集间的相似度。此时，可通过计算样本间的欧式距离D来衡量样本的相似度，当n=m时：

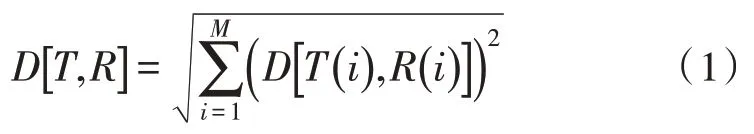
当n≠m时，需要引入动态规划的思想进行D的计算。

如图1所示，将测试样本的序号在直角坐标系的x轴上标注；将训练样本在y轴上标注。此时，可以在坐标轴上形成纵横交错的网格，网格的交叉点是测试样本与训练样本的交汇。同时需要寻找一条从坐标轴左下角出发右上角结束的路径，将这条路径经过的第i个点记为(ni，mi)，路径函数记为：

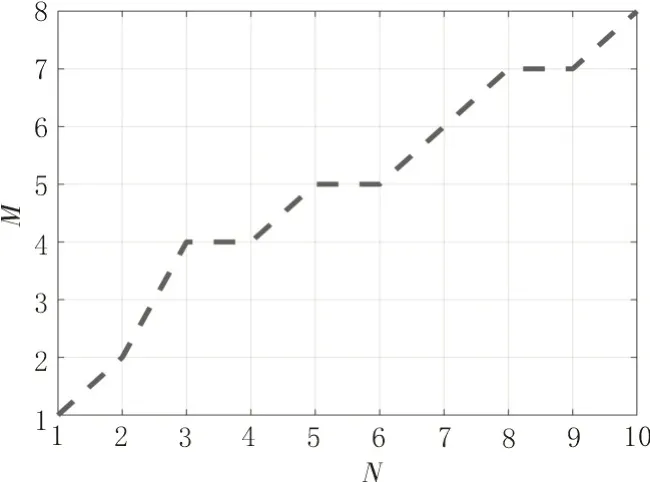
图1 DTW算法路径搜索原理

在路径搜索时，需要对斜率进行约束，以保证路径的走向，通常斜率的变化范围是0.5～2。当路径在当前时刻通过的点为(ni-1，mi-1)时，其下一点的所有可能情况为：

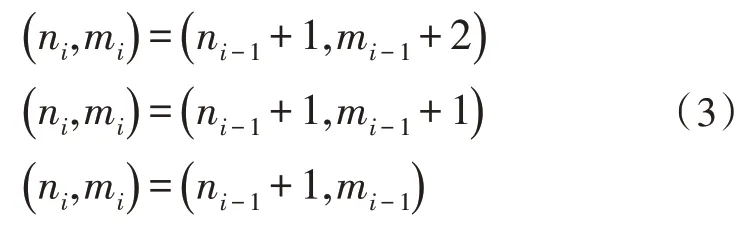
此时，将式（3）作为约束条件，求解式（1）中的最佳路径，以最短路径为优化目标，得到目标函数：

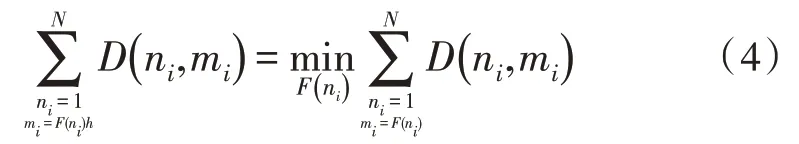
对于坐标轴中的任意点，在路径搜索的过程中，最终只有一条路径可以穿过。因此对于(ni，mi)，其路径上的前一点也只有3种情况，即(ni-1，mi)、(ni-1，mi-1-1)或(ni-1，mi-2)。此时，需要选择(ni，mi)点到这3 种情况下两点距离最短的点作为路径上的前一节点。此时，可以得到路径的总距离为：

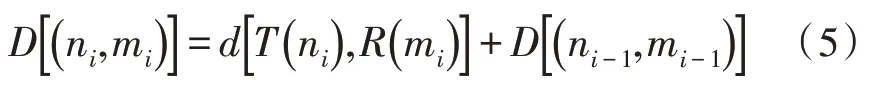
其中，ni-1和mi-1的确定方式如下：

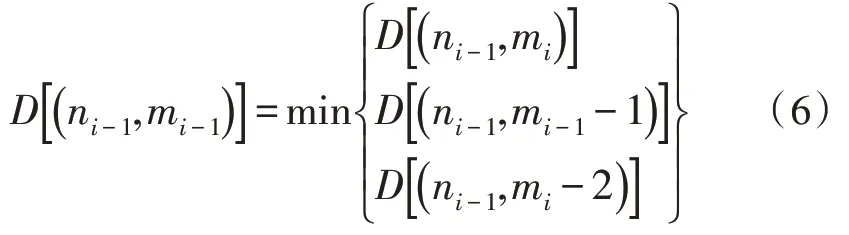
此时，可以通过逐点前向迭代的方式得到整条路径。

1.2 基于动态弯折的改进DTW算法

在上文中，DTW 算法在路径搜索过程中对于路径弯折的斜率进行了限制。但实际的迭代过程中，存在着无法满足该限制条件的点。以图2为例，图2中的菱形在进行距离匹配时，其格点之外的距离无需计算。由于菱形的几何特性，在计算中也无需保存所有步骤的累计距离。因此，可以在计算时间和计算开销上对1.1 节中的算法进行优化。

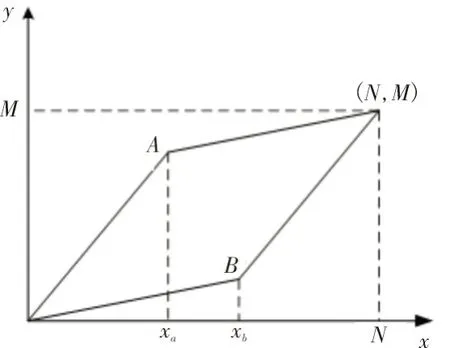
图2 算法路径约束示意图

在图2中，将实际的弯折划分为3 个路径段，分别是(1,Xa)、(Xa+1,Xb)、(Xb+1,N)，其坐标存在以下关系：

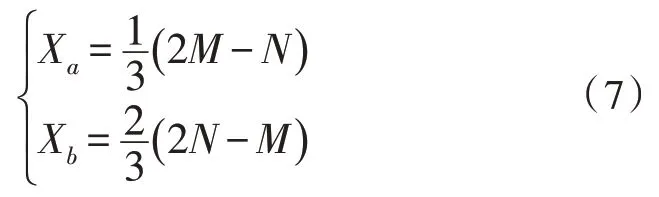
将Xa与Xb取为相近的整数，此时可以得到动态弯折匹配的约束条件：

引入动态弯折后，无需再将X轴上的特征向量与Y轴点对应的特征向量进行比对。只需要与[ymin，ymax]内的特征向量分别进行比对即可，这个区间端点的计算方式如下：

此时，距离累计的更新方法如下：

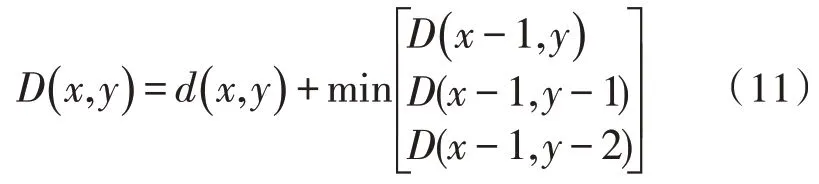
根据式（11）所示，当X轴上的时间标号逐步前进时，只需要关注前一列的累计距离即可。因此，该算法无需保存全部的距离矩阵，从而实现节省运行所需内存的目的。具体的更新方法如图3所示。

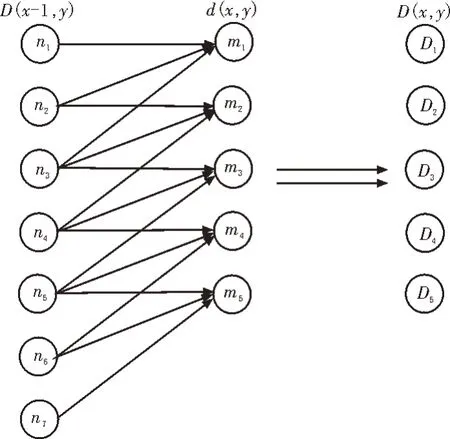
图3 累计距离更新方法

2 方法实现

2.1 实验设计

为了评估算法的性能，需要进行公司财务数据的搜集与清洗。该文选取了RESSET 金融数据库中对外公布的上市公司相关数据。在2010-2020年的所有公司中，剔除数据缺失的相关公司，筛选了100家上市公司。同时，该文还从该时间段内存在财务舞弊的公司中，筛选了100 家公司及其财务数据，共同组成了包含200 家公司的数据集。

该文实现算法的仿真平台参数如表1所示。

表1 计算环境参数

图4给出了基于DTW 算法的财务数据分析处理流程。

由图4可以看出，该文算法需要将财务数据表示为时间序列。对于一个单位，分别使用式（12）、式（13）作为训练样本和测试样本的时间序列标号：

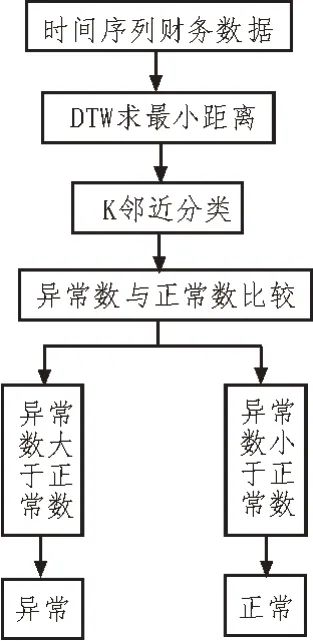
图4 算法流程

其中，m、n分别是训练样本和测试样本的时序标号，M、N分别是训练样本与测试样本对应的年份总数。在机器学习算法中，为了保障算法的性能，需要引入合适的特征对测试集、训练集的数据进行描述，这些特征组合为数据集的特征向量。特征向量的维度，对于算法的训练测试效果具有深刻的影响。在异常财务数据的识别中，需要引入表征财务特征的相关数据，该文引入的表征财务特征的数据如表2所示。

表2 算法使用的财务数据信息

根据图4所示的算法流程，基于DTW 算法计算时间序列的间距，然后使用K 邻近算法得到序列的分类结果。当同一公司正常的财务数据数大于异常数时，将该公司的状态置为正常；当该公司正常的财务数据数小于异常数时，将该公司的状态置为异常。

2.2 算法仿真结果

在进行算法的仿真时，为了提高获取的数据集的利用效率，文中使用k重交叉验证的方式进行算法的训练与测试。在k重交叉验证时，首先将所有的数据划分为维度相同的k个子集。在划分过程中，需要保证子集之间互不相交，且有同样的概率分布。然后选择其中的一个作为测试集，其余的作为训练集。交叉验证后，可以得到混淆矩阵。该文得到的混淆矩阵形式如表3所示。

表3 交叉验证混淆矩阵

在表3中，A 代表公司为异常、算法预测结果也是异常的公司；B 代表公司为异常、算法预测为正常的公司；C 代表公司为正常、算法预测为异常的公司；D 代表公司为正常、算法预测为正常的公司。该文在进行k重交叉验证时，取k为10，这样就得到了10 组预测结果。为了更优地评估算法性能，使用朴素贝叶斯分类算法进行对照实验，实验结果如表4所示。

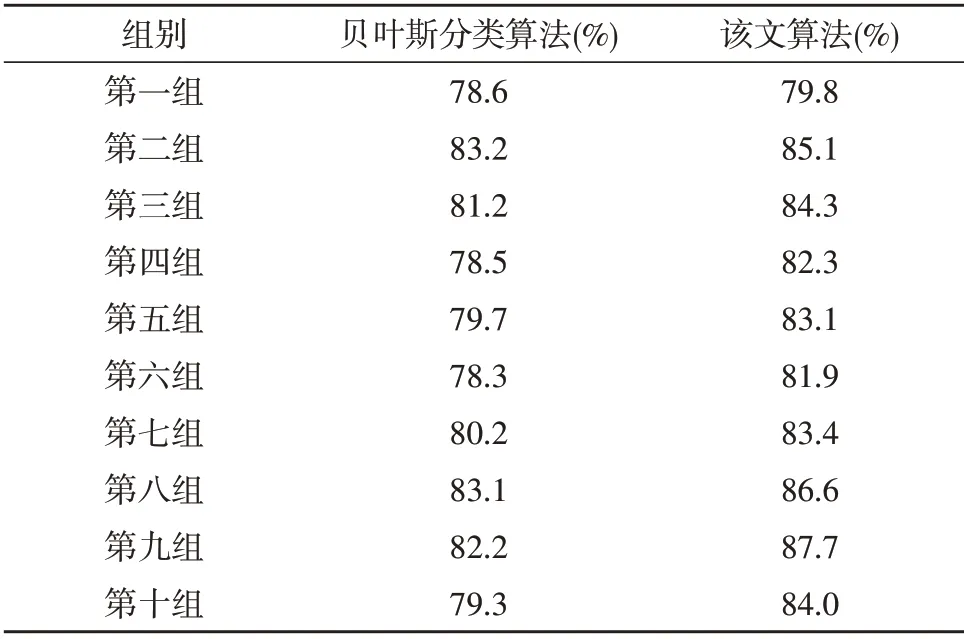
表4 基于BP神经网络的实验结果

从表4可以看出，该文算法在进行异常财务数据的识别时，每组数据的正确识别率基本都达到了80%，且均明显高于朴素贝叶斯算法的识别准确率。表4的结果证明了文中算法相较于现有的贝叶斯算法，在异常财务数据的识别上具有更优的性能和应用前景。

3 结束语

文中针对公司财务数据分析需求，从时间序列处理的角度进行了研究。基于动态时间规整算法，解决了不同时间维度下时间序列处理的问题。基于动态弯折的思想，算法在迭代过程中无需存储所有的距离矩阵，从而节约了算法运行时的存储需求。最终通过对比仿真，验证了文中算法可以取得比贝叶斯算法更优的识别正确率，说明该文算法可以应用到异常财务数据识别的场景中。