面向特征选择问题的差分鲸鱼优化算法

于航，王子谦，雷振宇，高尚策

（1.泰州学院计算机科学与技术学院，江苏泰州225300；2.富山大学工学部，日本富山9308555）

近年来，随机搜索算法已经被应用于全局优化问题。由于这些算法中随机算子的存在，相比确定性搜索算法而言，这些算法在运行时间和准确性方面展现出了极大的优越性。进化算法(EA)[1]是这些随机搜索算法中的一种。进化算法在求解目标函数的全局最优解时，采用随机算子来随机生成新的子代。进化算法由于在避免陷入局部最小的方面展现出了良好的性能，因此已逐渐成为研究人员所关注的热点，并被广泛地应用于各个领域。

一些已经被广泛使用的进化算法如下：粒子群优化算法（PSO）[2]是模拟鸟集群飞行觅食的行为，通过集体的协作使群体达到最优目的的算法；蚁群优化算法（ACO）[3]是一种模拟蚂蚁寻找食物来源的随机搜索算法；人工蜂群算法（ABC）[4]是一种模拟蜜蜂觅食行为的优化算法；遗传算法（GA）[5]借鉴了进化生物学中的遗传、突变和自然选择现象。当然，差分进化(DE)[6]和鲸鱼优化算法（WOA）[7]也属于其中。

在设计和使用这些元启发式算法时，对于搜索空间的探索能力和对于最优解的开发能力是一对既矛盾又需要被综合考虑的方面。近年来，研究人员发现采用混合元启发式算法可以有效地改善原算法这两方面的能力，并且混合算法展现出了良好的解决实际问题的能力。例如，文献[8]混合了粒子群算法（PSO）和人工蜂群算法（ABC）来训练前馈神经网络；文献[9]混合了鲸鱼优化算法（WOA）和模拟退火算法(SA)并应用于特征选择问题。

在数据挖掘和机器学习[10]中，实际问题中通常会涉及大量的特征。然而，并非所有特征都是必不可少的，许多特征是多余的甚至是不相关的，这些特征夹杂在其中可能会降低分类算法的准确性。而特征选择旨在通过仅选择特征集的一小部分子集来解决实际问题。通过删除不相关和冗余的特征，加快分类器的分类速度，简化学习的模型。

特征选择[11]是一项非常困难的任务，主要原因在于其搜索空间的维数十分庞大。假设一个数据集合具有n个特征，则其可能的解决方案总数为2n。随着数据收集技术的进步，这些问题越来越复杂，实际问题的特征数量n也会越来越大，遍历所有子集，从而选择一个合适的子集的难度更会越来越大。所以从实际上来说，搜索给定数据集的所有特征子集在大多数情况下是不可能实现的。于是，研究人员尝试利用多种搜索技术应用于特征选择，例如元启发式搜索和随机搜索。但是研究人员发现，大多数现有特征选择方法仍然遭受局部最小和停滞的困扰，且计算成本尤为高昂。因此，高效的全局搜索技术才能更好地解决特征选择问题。进化算法由于其强大的全局搜索能力，在特征选择领域中获得了研究人员的关注。文中同样尝试着用混合进化算法的方式来解决特征选择问题。

1 混合方法

1.1 鲸鱼优化算法的最优解开发

鲸鱼优化算法(WOA)是一种模仿座头鲸捕食猎物行为的算法。为了捕捉猎物，首先需要将猎物包围。其数学模型可用以下公式描述：

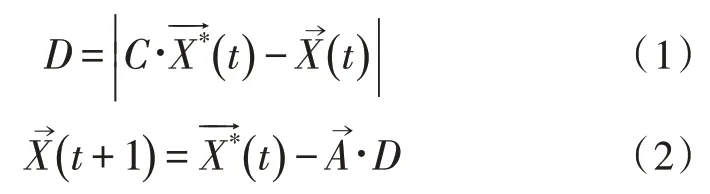
其中，t表示当前迭代，(t)表示到目前为止获得的最佳解决方案，X是位置矢量。另外，A和C是等式中的系数向量，计算方法如下：

其中，a在迭代过程中从2 线性减少到0，r是在[0,1]间隔内以均匀分布生成的随机向量。根据式（2），搜索单元（鲸鱼）根据最优解（猎物）的位置来更新其位置。调整A和C向量的值可以控制鲸鱼在猎物附近的区域。

算法通过式（3）中a值的减小实现了鲸鱼的收缩包围行为，其计算方法如下：

式中，t为迭代次数，M为允许迭代的最大次数。为了模拟螺旋形路径，计算了搜索单元（X）与迄今为止的最优解（X*）之间的距离，然后使用式（6）的螺旋方程式来获取临近搜索单元的位置：

为了对这两种机制建模，即收缩并环绕猎物和螺旋状的路径，在优化过程中，假设各有50%的概率选择其中的任意一种方式，如式（7）所示：

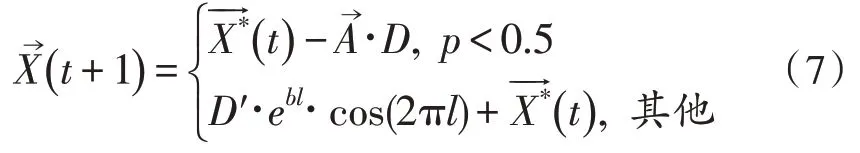
其中，p是在[-1,1]范围中的随机数。

1.2 差分进化算法

差分进化(DE)算法是众多进化算法的其中之一。近年来，结构简单的差分进化算法已展现出其快速解决优化问题的能力。受到遗传算法的启发，差分进化算法主要包括初始化、差分变异、交叉、选择。在初始化部分，假设有一个随机的NP维参数向量作为每一代的种群，定义如下：

在变异的环节，采用差分的方式来变异向量，定义如下：

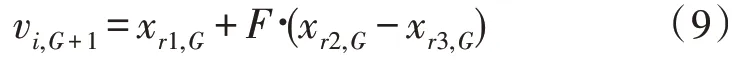
其中，r1,r2,r3 ∈[1,2,3,…,NP]是3 个随机数。F是差分因子且是一个常数，一般可以取0.5。G是指迭代次数。

为了增加种群向量的多样性，差分进化中设置了交叉的环节，对交叉的定义可以用如下的公式描述：

式中，rand是在[0,1]范围中的随机数。CR是交叉概率，一般取值为0.9。

最后一个选择的环节，顾名思义，就是去确定哪一个个体会被选择进入下一个种群。在差分进化中，采用了贪婪选择的方式，即代价函数值越小的个体，越需要被保留在种群中。于是，比较新获得的个体uji,G+1与过去的个体xji,G，若uji,G+1的代价函数值小于xji,G的代价函数值，则新个体uji,G+1取代旧个体xji,G保留在种群中。反之，则舍弃新个体uji,G+1。

1.3 基于鲸鱼优化的差分进化算法

上述介绍的鲸鱼优化算法(WOA)是近期提出的模仿座头鲸捕食猎物行为的优化算法，它展现出了解决优化问题的能力，并且已经被广泛地应用于各个领域。但是，鲸鱼优化算法的开发能力（如在式（2）和（6）中提到的一样）主要取决于到目前为止搜索单元与最优解之间的距离，所以首先需要有一个足够好的当前最优解，才能更好地利用鲸鱼优化算法的开发性能。于是设想采用一种有效的具有较强探索能力的算法来大致确定最优解的方位，再利用鲸鱼优化算法的开发能力找到最优解，从而提升搜索算法的能力。差分进化(DE)是众多进化算法的其中之一，它以其简单的结构和快速解决问题的能力，深受研究人员的关注。然而，差分进化算法具有较强探索能力的同时，开发能力却略显不足，因此，文中考虑结合鲸鱼优化算法和差分进化算法的优点，设计出了一种基于鲸鱼优化的差分进化混合算法。混合算法的流程图如图1所示。

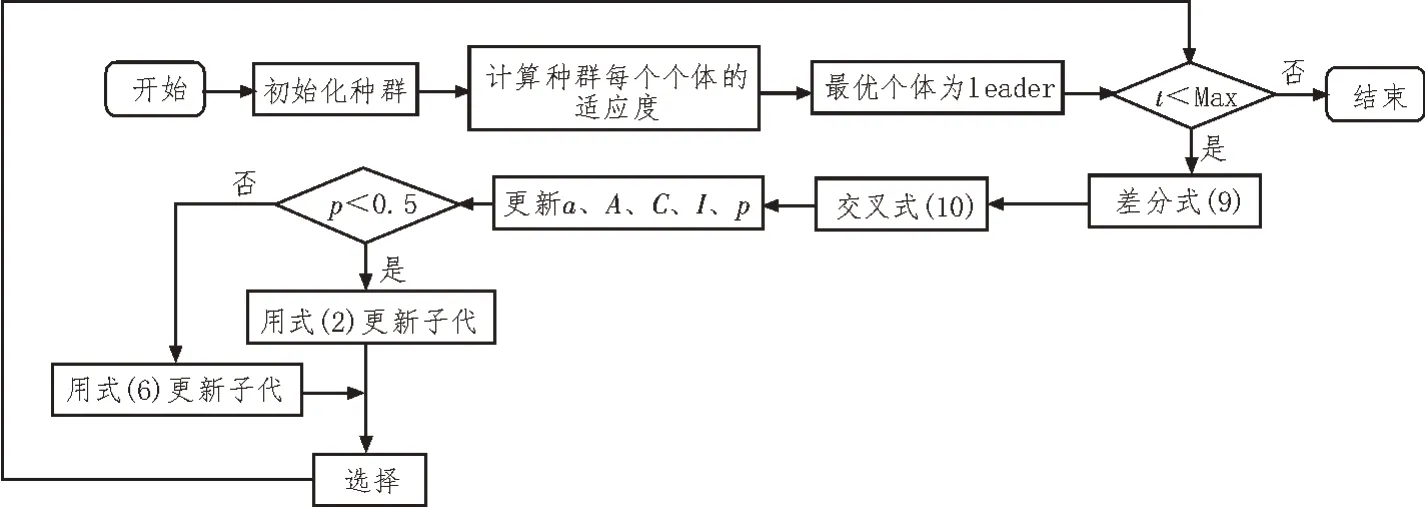
图1 混合算法流程图

2 进化特征选择

从本质上来说，特征选择问题是一个二进制优化问题，因为问题解决方案仅限于二进制{0，1}两个值。要将WODE 算法应用于特征选择问题，就需要设计一个二进制编码的版本。在这项工作中，解决的方案用一维向量来表示，向量的长度与原始数据集的特征数量相同。向量中的每个值都由“1”或者“0”来表示。用数值“1”表示选择相应的特征；而数值“0”表示不选择相应的特征。

特征选择问题可以看作是一个多目标优化问题，其中要实现如下两个目标：最少的特征数量和更高的分类精度。解决方案中选定的特征数量越少，分类的精度越高，则可以说解决方案就越好。每个解决方案的评价都需要使用代价函数，而代价函数主要利用KNN 分类器来获取解决方案中选定特征的分类精度。为了在解决方案中选定特征的数量（最小）和分类精度（最大）之间取得平衡，可使用如下方程式来定义代价函数：

其中，γR(D)表示给定分类器的分类误差，文中采用了K 邻近分类器。R表示所选子集的特征数量，N是数据集中特征的总数，α和β是与分类精度和选定子集长度有关的两个参数，α∈[0，1]，β=1-α。

3 仿真结果

3.1 函数集测试结果

下面将对提出的WODE 算法在CEC2017 函数集上进行测试。种群规模已设定为100，维度设置为30，最大迭代次数在算法中设置为3 000。此外，为了减小随机性带来的误差，算法在每一个函数上都会测试30 次，然后计算这30 次结果的平均值和标准偏差，得出最终结果。此外，将提出的WODE 算法与其他一些已经被广泛应用的进化算法进行比较，例如差分进化（DE）、鲸鱼优化算法（WOA）、粒子群优化算法（PSO），以显示提出算法的优越性。

上述提到的算法测试结果已经在表1中列了出来, 30 次独立运行结果的平均值表示算法的平均性能，而标准偏差（Std）反映了算法的鲁棒性，4 种算法对每个函数求解的最优解的最小值已经被加粗，如表1～表4所示。

表1 CEC2017中单峰函数测试结果

表2 CEC2017中多峰函数测试结果

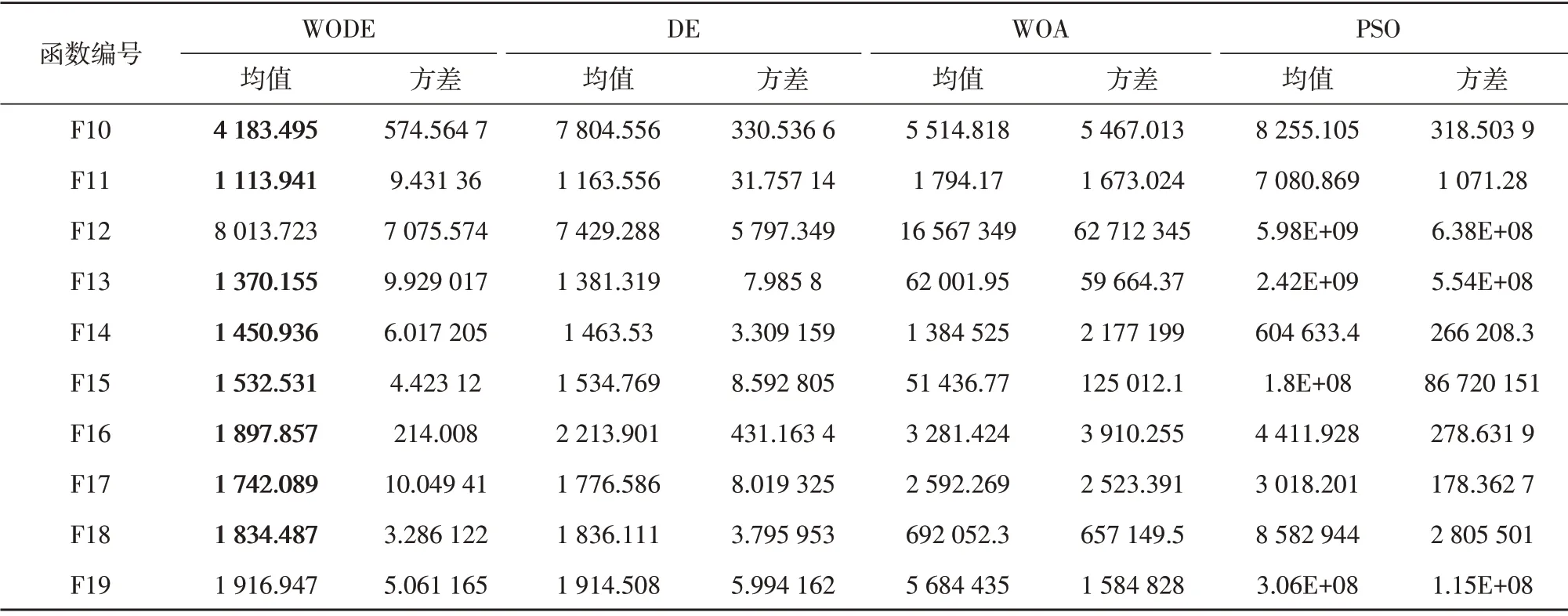
表3 CEC2017中混合函数测试结果

表4 CEC2017中组合函数测试结果

通过4 个表可以很明显看出，在5 个多峰测试函数和11 个组合测试函数中，WODE 比其余3 种算法的解更优。在4 个单峰测试函数中，WODE 有一半是最优。在10 个混合测试函数中，WODE 有8 个是最优。

图2是从30 个测试函数中随机抽取的4 个测试函数的数据所画的收敛图，从图2可以看出,WODE测试结果的最优值优于其余3 种算法。

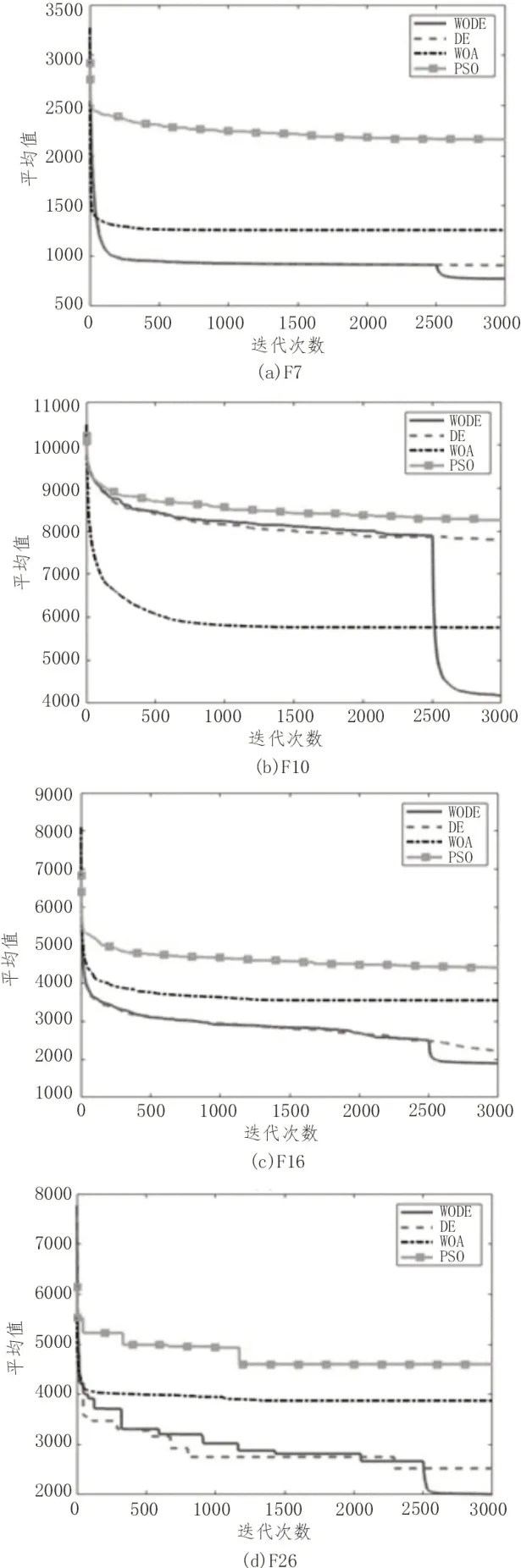
图2 收敛图

图3是随机选取的4 个测试函数数据的箱线图，从图3可以看出，WODE 的测试结果分布要优于其余3 个算法。

图3 箱线图

同时，Wilcoxon 检验[13]被用来精确比较WODE和其他测试算法之间的性能。Wilcoxon 检验是一种非参数检验，主要涉及两个样本的假设检验。实验中的置信区间设置为95%，即当Wilcoxon 检验之后得出的P值小于0.05 时，表示前者测试解的结果相比后者有显著性优势。表5列出了WODE 与DE、WOA、PSO 4 种算法的Wilcoxon 检验结果。从表5可以看出，WODE 的测试结果要优于其他3 种算法。

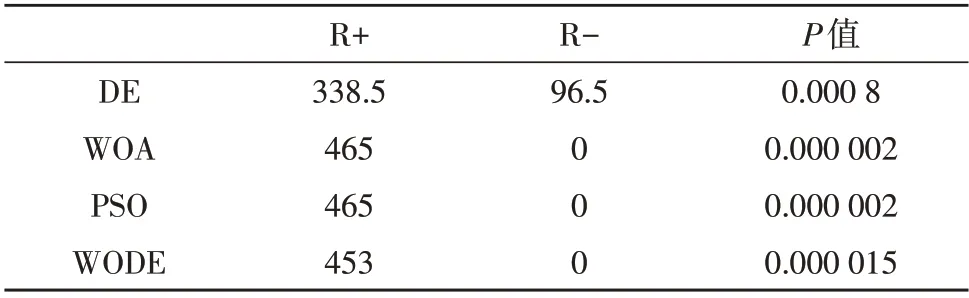
表5 Wilcoxon检验

3.2 特征选择的测试结果

文中还将所提出的混合算法WODE 应用于特征选择问题。同时，与DE、WOA 两种算法进行了比较，测试了算法的分类准确性和特征的数量。分类准确性取数据集运行30 次中的最优一次分类准确性，特征数量则为这30 次运行的平均特征数量。测试过程中，α取0.9。表6中列出了所采用的数据集基本信息，包括特征数量和数据集维度，测试用的3 个数据集均来自于UCI。

表7中罗列了算法的测试结果，其中，3 种算法中最优的分类准确性和最小的特征数量已经被加粗。从表7中可以明显看出，对于特征选择而言，WODE 的效果更好。

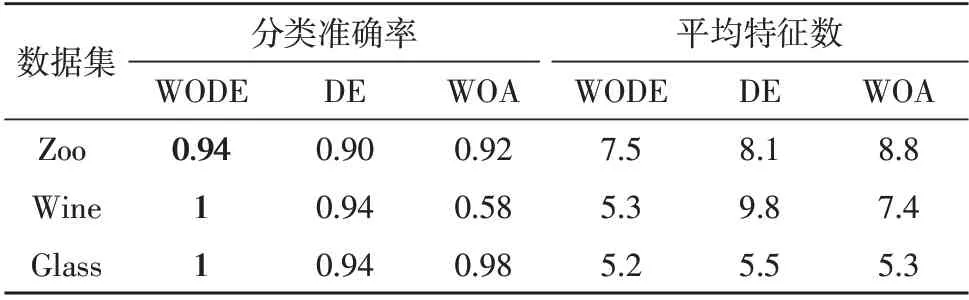
表7 分类准确率和特征的平均数量

4 结 论

文中提出了一种基于鲸鱼优化的差分进化算法，以提高进化算法的搜索能力。实验结果表明，提出的WODE 可以有效地提高DE 对于最优解的挖掘能力。此外，WODE 在处理特征选择问题时表现出了一定的优越性。在将来，将提出的WODE 应用于多目标优化问题[14]、组合优化问题[15]以及神经网络的学习[16]。