轨道交通铺轨加密三角高程测量及其数据处理方法研究

鲁勇，龚率

(1.成都市勘察测绘研究院，四川 成都 610081； 2.四川省城市信息化测绘工程技术研究中心，四川 成都 610081)

1 概 述

城市轨道交通轨道施工测量的传统做法是首先做铺轨控制基标测量，再做铺轨加密基标测量[1]。由于控制基标很多位于小半径曲线要素点上，因此铺轨基标测量存在：控制网型健壮性差、测量精度低且不均匀、依其铺设的轨道平顺性差、不适宜高速运行等缺点，同时由于铺轨基标通常埋设在隧道中下部突出位置，也不利于交叉作业时控制点的保护。由于引入高速铁路轨道交通测量技术，城市轨道施工测量传统方法的缺点大多可以被规避，现行城市轨道交通轨道施工测量逐步由传统的“基标+加密基标”作业模式转变为“任意设站控制网测量”的作业模式。

现行《城市轨道交通工程测量规范》对任意设站铺轨控制测量的技术方法有了明确的要求，但对任意设站铺轨加密测量方法未提及，铺轨高程加密测量仍然采用传统水准测量的方式，精度高，但费时费力，不经济。本文在任意设站铺轨控制测量方法的基础上，提出三角高程测量与数据处理新方法，着重分析其构网模型和差分数据处理原理，并通过实验证明三角高程测量结果与水准测量结果吻合较好，无须单独进行铺轨加密水准测量[2]，提高了作业效率，节约了施工成本，同时亦满足轨道交通铺轨施工要求。

2 任意设站铺轨加密网测量新方法

任意设站铺轨加密网是采用智能型全站仪自动观测的自由设控制网，其观测值是自由设站到铺轨控制点与铺轨加密点的水平方向值、斜距和竖直角[3]。采用自由设站观测，没有仪器对中误差，棱镜中心就是铺轨加密点或铺轨控制点的点位中心，没有目标对中误差和棱镜高量取误差，因而极大地减小了系统误差对平差结果的影响。自由设站的位置一般选择在本测站所观测的铺轨加密点区域的中心，同一测站观测的铺轨控制点应不少于3对，相邻铺轨控制点间距为 40 m～60 m；同时观测左右侧对称的10对～14对铺轨加密点，相邻铺轨加密点的间距约 4.5 m～6 m，下一测站要求联测上一测站4对～5对铺轨加密点，如图1所示。在测站1内观测301～308共4对铺轨控制点(部分铺轨控制点未画出)，观测L01～L12与R01～R12共12对铺轨加密点；在测站2内观测303～310共4对铺轨控制点，观测L08～L20与R08～R20共13对铺轨加密点[3，4]。

根据自由设站到铺轨加密点或铺轨控制点的斜距与竖直角，就可以计算自由设站到各铺轨加密点或铺轨控制点的三角高差。这样的三角高差是单向的，地球曲率和大气折光的影响未消除，无法满足高精度高程控制网的精度要求。由于自由设站到相邻两铺轨加密点的距离大致相等，因此可采用自由设站点到两相邻铺轨加密点的直接高差进行差分处理，得到相邻铺轨加密点的间接高差作为观测值，这样的间接高差不仅基本消除了球气差的影响，还构成了若干闭合环和附合路线，如图2所示。

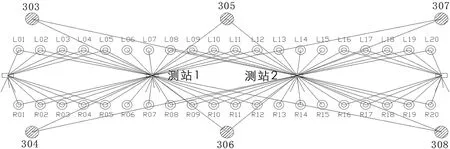
图1 任意设站铺轨加密网测量新方法示意图

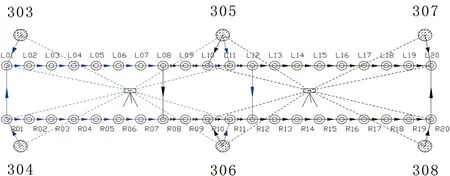
图2 加密三角高程网高差传递示意图

加密三角高程网的起算数据为该网内铺轨控制点的高程，为了减小铺轨控制点向铺轨加密点传递高程时球气差的影响，同样，对自由设站点到铺轨控制点和其邻近的铺轨加密点的高差进行差分处理，如图2中303与L01组成间接高差，308与R20组成间接高差。为了控制数据质量，加密三角高程网的附合或者闭合路线的闭合差，应满足式(1)的要求。

(1)

式(1)中，fh表示附合或者闭合路线的闭合差，单位为mm；S表示附合或者闭合线路长度，单位为km。

数据处理时，可把沿线路方向每相邻两个测站所构成的三角高程网单独平差计算，同一个三角高程网内的相邻两个测站需重复观测4对～5对铺轨加密点。对于相邻两个三角高程网，可搭接3对铺轨加密点，如果这些搭接点在两个网中分别平差后的高程较差小于 0.6 mm，就用余弦函数平滑原理[4]求搭接点的高程。

3 三角高程网数据处理

要合理地消除加密三角高程网中的闭合差，就必须对该网中的间接高差进行平差处理。平差前，需要确定网中相邻铺轨加密点间或者铺轨控制点到邻近铺轨加密点的高差观测值的权比关系。显然，常规水准网中按距离或者测站数定权已不再适应加密三角高程网。考虑到加密三角高程网中高差的测量误差与自由设站到铺轨加密点或铺轨控制点的斜距和竖直角测量误差有关，因此可根据斜距与竖直角的测量中误差，按照误差传播定律求出加密三角高程网中各高差的中误差，进而确定加密三角高程网中各高差观测值的权值[4]。

相邻铺轨加密点的高差(或者铺轨控制点到邻近铺轨加密点的高差)为自由设站到各点的直接高差之差，那么两相邻加密(或铺轨点与邻近铺轨加密点)i、j之间的高差hij为：

-(Sicosαi)2]

(2)

式中，Sj、Si为自由设站到j和i两点的斜距，αj、αi分别为测站到i、j两点的竖直角，R为地球曲率半径，K为大气垂直折光系数。

由于K值小于1，R很大，并且Sj与Si大致相等，故可以将上式近似简化为：

hij=Sjsinαj-Sisinαi

(3)

对式(3)全微分，可得：

(4)

根据式(4)，由误差传播律，可得高差中误差与竖直角和斜距测量中误差的关系为：

(5)

式(5)中，mhij为两相邻i、j点高差的中误差，mSi、mSj分别为测站到i、j两点斜距测量的中误差，mαi、mαj分别为测站到两点i和j竖直角测量的中误差，ρ″=206265。i、j两点间高差观测值的权为：

(6)

式(6)中，δ0为单位权中误差，可取全站仪竖直角测量的标称精度作为其值。

对于三角高程网内搭接点处的铺轨加密点，存在同名高差，可采用加权平均方法进行合成。设hA、hB为不同自由设站观测值计算得到的同名高差，权分别为pA、pB，h为合并后的高差，其权为P，则同名高差加权合成后的高差h及其权值P可分别按式(7)和式(8)进行计算[5]：

h=(pAhA+pBhB)/(pA+pB)

(7)

P=pA+pB

(8)

加密三角高程网，按图2组成间接高差观测值，并按式(6)确定各观测值的权。以该网中的铺轨控制点高程作为起算数据，依据间接平差原理[6]，可以求出该网内的铺轨加密点在最小二乘准则下的最佳估值和其高程中误差，并按误差传播定律求出各相邻铺轨加密点的高差中误差。

4 加密三角高程网相对精度仿真计算

根据本文所提出的任意设站铺轨加密三角高程网的网形，参考主流智能型全站仪的标称精度给定先验精度(测角精度为±1″，测距精度为±(1+1×10-6D)mm)，根据经典间接平差原理，推估加密三角高程网中相邻点高差中误差的大小，如表1所示。

加密三角高程网模拟相邻点高差中误差仿真计算结果统计表 表1

由表1可知，模拟仿真计算加密三角高程网的相邻点相对高差中误差最大不超过 ±0.9 mm，绝大部分位于 ±0.6 mm以内，具有很高的精度，以此指导轨道铺设亦能保持良好的平顺性。

5 实验结果分析

为验证上述加密三角高程网理论的可行性，依据铺轨控制网与加密的布点要求，在成都轨道交通6号线某 1.5 km长的隧道区间按本文的布网要求，布设了300对铺轨加密点和30对铺轨控制点，按本文介绍的测量方法，采用Leica TS15仪器进行加密三角高程测量实验。将采集的数据进行平差计算的结果表明，采用该加密三角高程网中的铺轨控制点的高程作为起算数据进行平差，铺轨加密点间的后验高差中误差有较高精度，其平差成果与铺轨加密点水准测量成果也更接近，具体情况如表2、表3所示。

加密三角高程网相邻点高差中误差平差统计表 表2

由表2可知加密三角高程网平差后铺轨加密点的高程中误差在 ±1.0 mm以下的达94.4%，最大也不超过 ±1.2 mm，顾及已知点的兼容性问题和实测现场的环境差异，该平差结果与其仿真计算结果是高度一致的。说明该网形设计合理，数学模型可靠，铺轨加密点高程精度较高。

加密三角高程网平差高程与水准高程较差的绝对值统计表 表3

由表3可知，加密三角高程网平差后铺轨加密点高程与相应水准高程较差在 ±1.2 mm以下的占91.3%，在 ±1.6 mm以内的达100%，即没有超过 ±1.6 mm的高程较差。说明加密三角高程网与铺轨加密点水准数据处理结果差异较小。

6 结 论

通过上文对加密三角高程测量和数据处理方法的介绍及相应观测实验结果的分析，可以得出如下结论：

(1)智能型全站仪的测距测角精度很高，特别是对短距离的测量有优势，本文所提出的基于差分原理的加密三角高程网的平差结果精度高、稳定可靠，可以满足轨道交通工程铺轨的施工要求，值得进一步深入研究；

(2)本文所提出的加密三角高程网和加密平面网采用的数据一致，减小了因高程测量与平面测量的仪器不同，测量标志不同所造成的加密高程测量点和平面测量点不对应的问题；

(3)由于铺轨加密点采用与铺轨控制点相同的强制对中标志，每站测量前可先在所有铺轨加密点标志上一次性装好棱镜，然后进行观测。由于所有铺轨加密点都强制对中，没有对中误差的影响，因此铺轨加密点测量精度较传统方法高；

(4)本文所提出的加密三角高程网利用了加密平面网测量新方法的外业观测数据，节约了成本，提高了测量效率，具有良好的应用前景。