可再生能源电力系统的虚拟同步发电机频率控制策略

李玲玲，冯 欢

（1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300130）

光伏、风力等可再生能源发电在电力系统中占比越来越高，可再生能源发电输出功率具有波动性和随机性的特点[1-2]，增加了电力系统的功率不平衡程度。而且可再生能源发电并网逆变器没有旋转储能结构，这降低了系统的惯性和阻尼特性[3]，不利于电力系统在扰动下的频率稳定[4]。可再生能源的占比越高，这种影响也会越大[5]。这些问题限制了可再生能源发电的应用[6]，不利于环境的可持续发展。

为了解决可再生能源电力系统惯性低、频率稳定性差的问题，可应用虚拟同步发电机（VSG）技术[7]，在不牺牲系统惯性和频率稳定性的前提下将可再生能源发电接入电力系统[8]，提高系统抑制频率波动的能力[9]。目前，有关VSG的研究主要包括：系统的稳定性、VSG并网预同步问题和VSG优化控制问题。文献[10]分析了VSG的控制参数与系统稳定性的关系，不仅研究了VSG控制，而且对参数进行了量化设计，提高了系统的稳定性；文献[11]针对VSG过大的虚拟惯性会导致电源振荡问题，建立了带有并联VSG的微网小信号模型，通过控制算法调整虚拟电抗，达到了提高系统稳定性和动态响应中有功功率的精度的目的。文献[12]引入虚拟阻抗模拟同步电抗，保障了系统孤岛运行的基本稳定，同时还完成了并网至孤岛的平滑切换；文献[13]研究了VSG的综合切换控制策略，控制策略包括准同步算法和孤岛监测算法，提高了电源的可靠性和质量。文献[14]基于小信号稳定性分析了含VSG微电网的电能质量主动控制策略，在原有双闭环控制器的基础上设计了控制器，达到谐波抑制的效果，运用了优化方法，但未对控制参数进行优化；文献[15]在原有VSG控制基础上，引入频率偏差的积分控制，使换流器不仅参与交流系统一次调频，而且参与二次调频工作，这种方式实现了交流系统的无差控制，但同样缺少对控制器参数的优化研究；文献[16]研究了基于双馈异步发电机的风力发电机组虚拟同步控制，可以为低短路比的弱电网提供惯性支撑，研究扩展了VSG的应用场景；文献[17]建立了微电网完整小信号状态模型，研究了VSG接入后的微电网稳定性，提出的控制策略有效稳定了系统的频率，达到了预期目标；文献[18]提出的控制策略将电压源模式转换为电流源模式，可以在电网故障时通过比例谐振电流控制算法限制输出电流，向电力系统提供无功功率支撑，提升了系统在不同状态下的稳定能力。由此可见，绝大多数文献研究VSG优化控制问题，着重讨论了VSG控制在不同场景下的适应性和稳定性，提出了控制策略，却未进一步研究VSG控制参数的优化，而控制参数对控制策略性能的提升有着重要帮助。

针对这一问题，为了进一步提升VSG控制系统的性能，也为了拓展智能算法在VSG参数优化问题上的应用，本研究提出一种基于改进蚁狮算法优化的VSG控制策略。针对优化问题的特性对蚁狮算法进行改进，应用改进的蚁狮算法优化VSG控制器的参数，使VSG的频率控制效果达到最佳。

1 VSG控制策略

同步发电机调节系统频率包括惯性调节、一次频率调节和二次频率调节3个过程。

（1）惯性调节过程：同步发电机转子旋转时储存动能，与系统保持同步运转，其旋转状态不会发生突变。当系统频率发生波动时，转子通过增减自身动能补偿系统功率的缺额。

（2）一次频率调节：调速器根据发电机转速变化线性调节原动机输入功率，系统功率缺额进一步减小。

（3）二次频率调节：通过调频器作用实现无差调节。

在设计VSG控制器时，考虑了同步发电机的上述功能，从而使VSG具备与同步发电机相似的惯性和频率调节功能。

1.1 虚拟惯性和阻尼特性

同步发电机的转子具备惯性特性，其存在如式（1）所示的关系：

式中：s为一个复变量；PM为输入机械功率；PL为负载功率；f为系统频率；H为转子的转动惯量；D为阻尼系数。

在VSG控制系统中设计了“虚拟转子”的功能，虚拟转子的功能由式（2）描述：

式中：Pref为VSG输出的功率；Hv为VSG的虚拟惯量；Dv为虚拟阻尼系数。

1.2 虚拟一次调频和虚拟二次调频

同步发电机的调速器在频率偏移之后调节输入机械功率，补偿功率量和频率偏移量呈现比例关系，所以可以在VSG中设计相应的比例环节，实现VSG一次调频的功能。同步发电机二次调频是调节系统频率到额定值，所以设计了积分环节，实现虚拟二次调频的作用。控制关系可由式（3）描述：

式中：K1和K2分别为虚拟一次调频增益和虚拟二次调频增益；ΔP为虚拟一次调频和虚拟二次调频根据系统频率的偏移量所调节的输出功率量。

1.3 虚拟控制器结构设计

虚拟控制器的结构如图1所示。

图1 虚拟控制器结构Fig.1 Structure of virtual controller

本研究提出的虚拟控制器由频率调节环节和虚拟转子组成。其中，频率调节环节包括一个比例调节回路和两个积分调节回路，分别模拟同步发电机的一次和二次调频功能。虚拟转子环节保证控制回路具有一定的惯性和阻尼特性，从而使VSG具备了同步发电机的惯性调节功能。VSG将参与系统的一次和二次频率调节任务，以保证系统频率偏差最小。电力电子逆变器的输出跟随指令信号变化，视为一阶惯性环节。K3为控制器积分环节增益。

2 基于改进蚁狮算法的控制参数优化

由前文可知，控制器的频率调节性能受系数K1、K2和K3影响，选择这些参数要考虑控制器的补偿容量和系统的稳定性能，运用数学方法求解参数受到的约束条件多，求解过程繁琐。为了更好地发挥控制器的性能，本文应用蚁狮算法（antlion algorithm，ALO）对参数进行优化。蚁狮算法收敛速度快、收敛精度高，经过改进，适用于所研究问题的优化。

虚拟控制器的传递函数如式（4）所示，改进蚁狮算法用于优化控制器参数的取值，目的是使系统达到最佳的控制性能，所以改进蚁狮算法的优化目标函数是系统频率偏差的平方和。目标函数最终形式如式（5）所示：

式中：Obf为算法的目标函数；tsim为仿真运行时间；Δf为系统频率偏差值。

蚁狮算法[19]的主要灵感来自蚁狮的觅食行为。蚁狮狩猎时会在沙子里挖锥形的陷阱，陷阱的边缘足够光滑，蚂蚁很容易掉到陷阱的底部，蚁狮将自身藏在陷阱的底部，等待蚂蚁掉入陷阱。一旦蚁狮意识到有蚂蚁掉入陷阱，蚁狮会向坑边扔沙子，阻止蚂蚁逃离陷阱，并伺机抓住蚂蚁。蚁狮完成一次捕食后，会重新修正陷阱，以备下次捕猎。受到蚁狮捕食的启发，蚁狮算法的优化过程如下。

（1）蚂蚁的随机游走。每个蚂蚁代表一个尝试解，蚂蚁通过随机游走更新自己的位置。式（6）可以保证蚂蚁游走不会超出搜索空间。

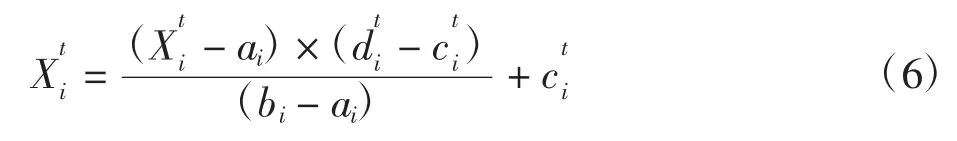
式中：ai为蚂蚁随机游走步长的最小值；bi为蚂蚁随机游动步长的最大值；为第i个蚂蚁第t次迭代时的最小值；为第i个蚂蚁第t次迭代时的最大值。

（2）陷入蚁狮的陷阱。蚂蚁在随机游走的过程中会受到蚁狮陷阱的影响，由式（7）和式（8）表达：

式中：ct为所有蚂蚁第t次游走时的最小值；dt为所有蚂蚁第t次游走时的最大值；为第i只蚂蚁所有变量的最小值；为第i只蚂蚁所有变量的最大值；Antliontj为第j个蚁狮第t次迭代时的位置。

（3）设置陷阱。为了模拟蚁狮的捕猎能力，采用了轮盘赌机制。在ALO算法中，假设蚂蚁只会被困在一个陷阱中。在优化过程中，ALO算法根据蚂蚁的适应度借助轮盘赌机制选择蚂蚁，这样就给适应度更高的蚁狮有更大的机会捕捉蚂蚁。

（4）蚂蚁滑向蚁狮。意识到猎物掉到陷阱里，蚁狮的行为会使猎物一点点滑落接近自己。数学上通过减小蚂蚁随机游走的半径来表示这种行为，如式（9）—式（11）所示：

式中：t为当前迭代次数；T为最大迭代次数；w为随着迭代次数改变的常数。在经典的蚁狮算法中，算法所定义的参数w的取值区间不适于研究中问题的寻优。原始算法中，迭代次数默认设置的比较大，基于提高仿真模型运行效率的目的，本文迭代次数设置的比较小。如果不改进w的取值，会导致w取值跨度增大，影响算法的精度，所以对w的取值区间做了改进。改进前后w的取值区间如表1所示。

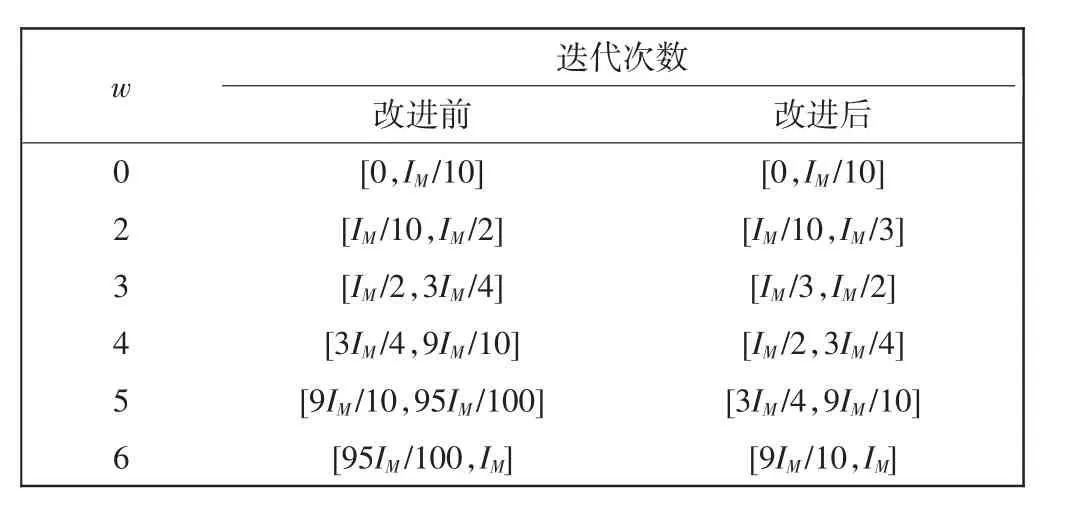
表1 改进前后参数w的取值区间Tab.1 Values range of parameter w before and after improvement

（5）蚁狮捕获猎物并重新修筑陷阱。狩猎的最后阶段是蚂蚁到达坑底并被蚁狮抓住，蚁狮把蚂蚁拉进沙子里并吃掉它。为了表达这个过程，假设蚂蚁的适应度变得比与之对应的蚁狮更高时，蚁狮就会捕捉蚂蚁。随后，蚁狮将更新自身的位置到被猎杀蚂蚁处，以提高捕食的机会。对此，建立式（12）：

（6）精英策略。精英策略是进化算法的一个重要特征，它允许进化算法保持在优化过程的任何阶段获得的最优解。在这项研究中，迄今为止在每一次迭代中获得的最佳蚁狮被保存下来，并被视为精英。精英是适应度最高的解，它应该在算法优化的过程中参与到解的更新中，也就是影响蚂蚁的移动。所以，蚂蚁的移动公式由式（13）确定：

综上所述，改进的蚁狮算法优化控制器参数的过程总结如下：

（1）初始化蚁狮算法，根据解决问题的需求设置迭代次数、种群规模等参数；

（2）初始化种群，运行初始化程序，每个个体都代表问题的一个特定解，记录最优个体等参数；

（3）迭代更新，根据算法的机制更新蚁狮和蚂蚁的位置，并计算个体的适应度；

（4）更新运行参数，记录每次迭代过程的最优解。满足算法结束条件时，转到步骤（5），否则，返回步骤（3）；

（5）算法结束，输出最优解。

3 实验验证

3.1 实验设置

风力发电模型如图2所示。

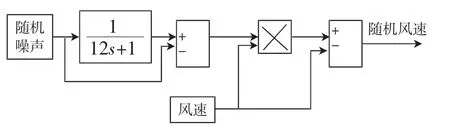
图2 随机风速模型Fig.2 Model of random wind speed

风力发电的输出功率由式（14）计算：

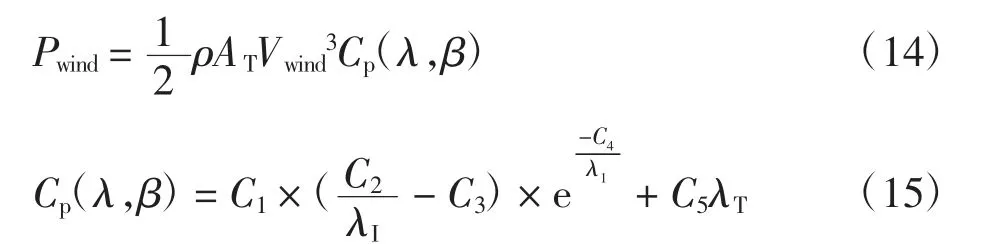
式中：ρ为空气密度（kg/m3）；AT为转子的旋转面积（m2）；Vwind为风速（m/s）；Cp（λ，β）为转化系数；β为桨距角；λT为最佳尖速比；C1—C5为涡轮系数。

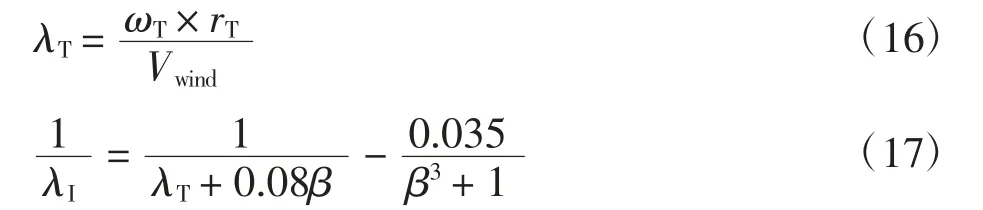
式中：ωT为风机转子转动的角频率；rT为转子半径；λI为由λT和β决定的间歇性最佳尖速比。风力涡轮机单元的参数值如表2所示[20]。

表2 风力发电厂参数Tab.2 Parameters of wind power plant

光伏发电模型如图3所示。

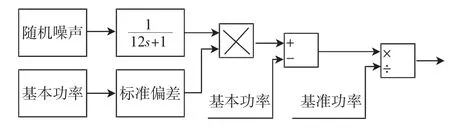
图3 光伏模型Fig.3 Photovoltaic model

光伏输出功率由基本功率和随机波动功率组成，随机波动功率由Random noise模块模拟，功率偏差由式（18）确定：

负载模型如图4所示。

图4 负载模型Fig.4 Load model

负载功率也由基本功率和随机波动的功率组成，通过式（19）模拟负载偏差：

式中：ΔPLoad为负载偏差；PLoad为基本负载功率。

根据上述的光伏、风电和负载模型，结合埃及电力控股公司年度报告中提供的数据，建立了埃及实际电力系统的仿真模型，如图5所示。将提出的VSG控制策略与传统控制策略进行对比实验，验证本文提出的控制方法的性能。

图5 电力系统仿真模型Fig.5 Simulation model of power system

本文建立的埃及电力系统仿真模型包括多种类型的发电厂。根据埃及电力控股公司2017年年度报告提供的数据设计电力系统仿真模型的参数，相关参数的配置如表3所示。

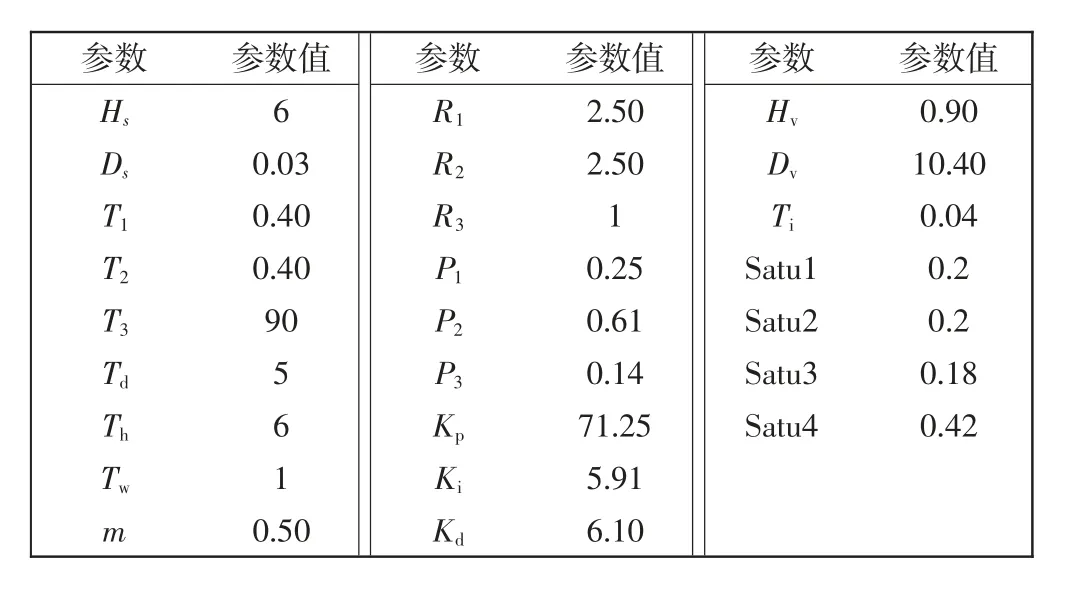
表3 埃及电力系统参数Tab.3 Parameters of Egyptian power system

表3中，Satu1、Satu2、Satu3分别为传统能源发电厂的电源容量限制功率，Satu4为VSG的调节容量限制功率。表3中：P1、P2、P3和R1、R2、R3为调节各类发电厂出力的比例系数；Kp、Ki、Kd为比例积分微分调节系数，用于调节发电厂在频率偏移时的补偿功率；T1、T2、T3等为时间常数，用于模拟发电厂机械设备调节输出功率的延时；Td为发电机转子的惯性常数；m为调节输出功率和系统平衡的系数。比例系数和时间常数无单位。

3.2 ALO算法的优化结果

应用ALO算法优化控制器参数，通过最小化目标函数，算法将找到适合系统的最佳控制器参数，使系统的频率稳定性达到最优。ALO算法的优化结果如表4所示。

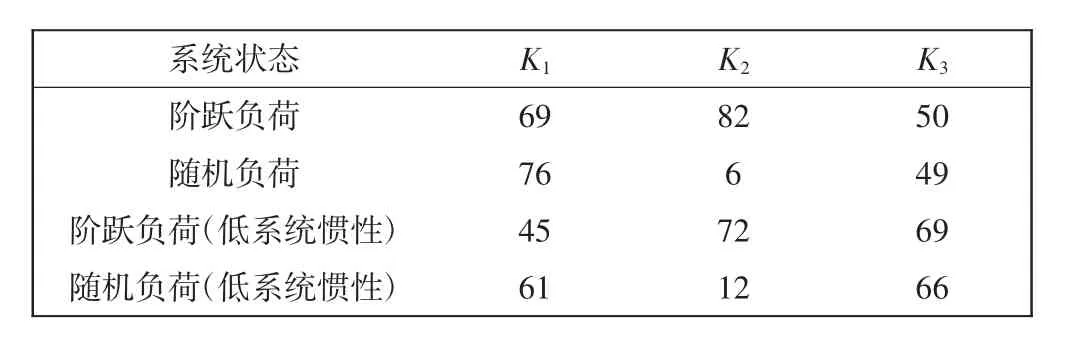
表4 ALO算法优化结果Tab.4 Optimization results of ALO algorithm

3.3 VSG控制方案的对比测试结果

将所提出的VSG频率控制方案与常规的一次和二次频率控制方案的结果进行对比，以验证所提方案的优越性。

3.3.1 阶跃负荷测试

在t=500 s时将阶跃负荷接入电力系统仿真模型中，负荷值为0.05 pu，以检验系统应对阶跃负荷的稳定性，结果如图6所示。

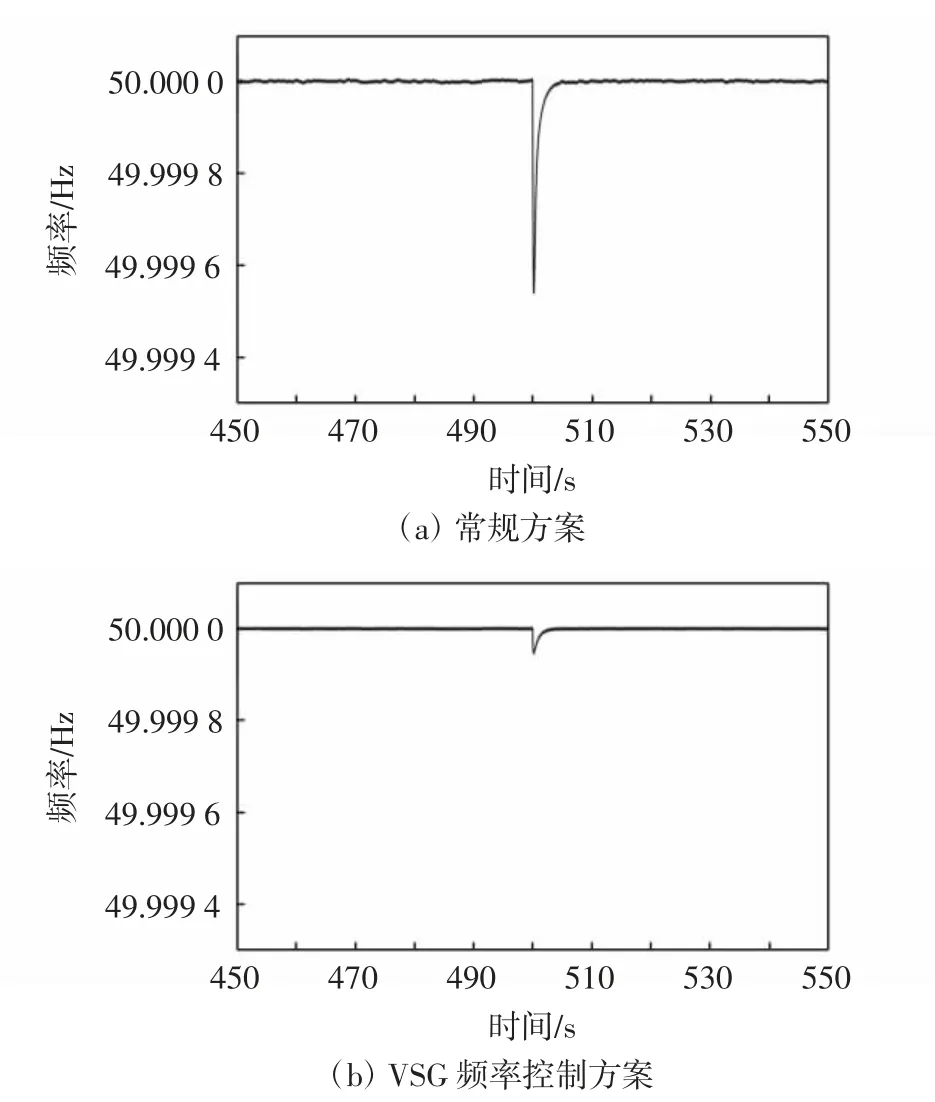
图6 阶跃负荷测试结果Fig.6 Result of step load test

由图6可以看出，由于在t=500 s时系统接入了阶跃负荷，2种控制方案均出现频率下降现象。采用VSG控制策略由于增加了系统的惯性，使得频率波动更小，频率波动幅度约为0.000 05 Hz，频率波动时间约为2.5 s。反观传统控制，由于未向系统提供惯性支撑，在负荷扰动期间，频率波动较大，波动幅度约为0.000 47 Hz，波动时间约为4 s。采用VSG控制策略使得系统频率的波动幅度降低了约0.000 42 Hz，波动时间降低了约1.5 s。

3.3.2 随机负荷扰动测试

在t=500 s时，向系统中加入随机变化的负荷，负荷图形如图7所示，以模拟现实生活中随时接入电力系统中的大规模随机负荷。实验结果如图8所示。

图7 随机负荷功率Fig.7 Random load power

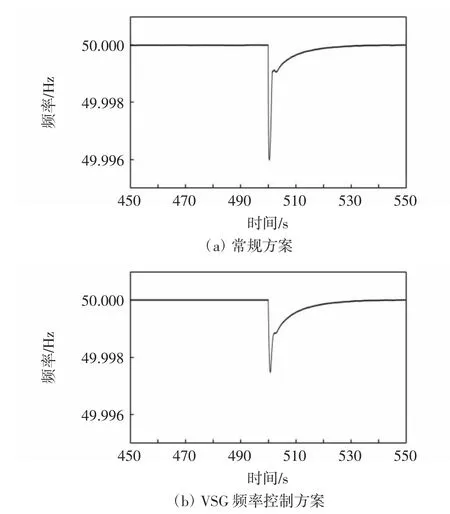
图8 随机负荷扰动模拟测试结果Fig.8 Test results of random load disturbance simulation

由图8可以看出，在t=500 s时接入了随机变化的负荷，系统频率下降，两种策略的频率波动时间大致相同。在幅值方面，VSG控制方式的系统频率偏移了约0.000 27 Hz，传统控制方式频率偏移了约0.000 4 Hz。在时间方面，VSG控制方式的系统频率偏移了约15 s，传统控制方式频率偏移了约17 s。采用VSG控制策略可使得系统频率的波动幅度降低约0.000 13 Hz，波动时间降低约2 s。从上述比较中可以看出，本文提出的VSG控制策略增加了系统的频率稳定性，验证了频率控制方案的有效性。

3.3.3 降低系统惯性测试

在将系统的整体惯性降低50%之后，再做上述实验，以验证控制策略的适用性。阶跃负荷和随机负荷的测试结果如图9和图10所示。

由图9和图10可以看出，系统惯性下降，相同负荷扰动下，频率波动幅度有所上升。VSG控制策略在阶跃负荷扰动下频率偏移了约0.000 09 Hz，偏移时间约为2 s，在随机负荷扰动下频率偏移了约0.000 36 Hz，偏移时间约为12 s；传统控制策略在阶跃负荷扰动下频率偏移了约0.000 54 Hz，偏移时间约为4 s，在随机负荷扰动下频率偏移了约0.000 5 Hz，偏移时间约为13 s。采用VSG控制策略可使得系统频率的波动幅度在阶跃负荷扰动下降低约0.000 45 Hz，在随机负荷扰动下降低约0.000 14 Hz，波动时间在阶跃负荷扰动下降低约2 s，在随机负荷扰动下降低约1 s。2种控制方式相比较，VSG控制的系统频率偏移更小，频率稳定性更好。

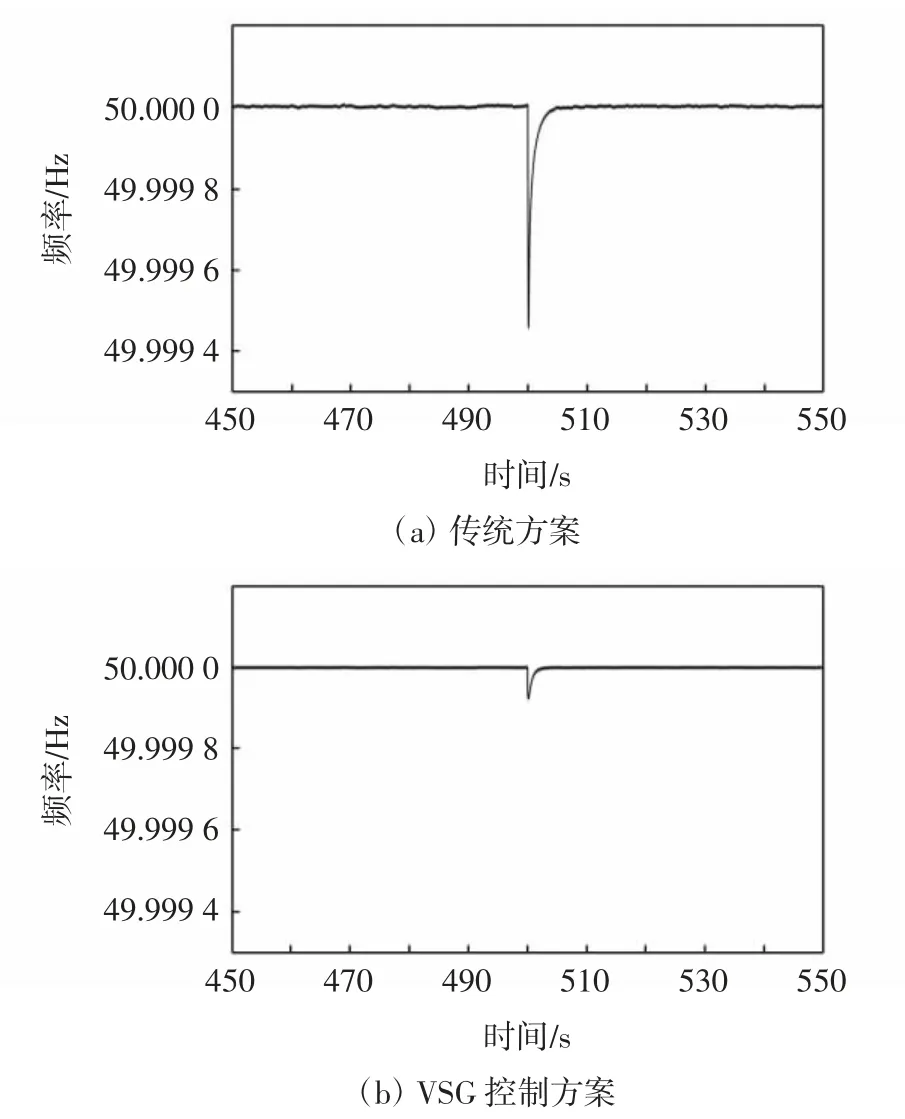
图9 系统惯性降低50%后阶跃负荷测试结果Fig.9 Test results of step load after system inertia reduced by 50%

图10 系统惯性降低50%后随机负荷测试结果Fig.10 Test results of random load after system inertia reduced by 50%

综上所述，在不同系统惯性条件下，无论是阶跃负荷变化，还是随机负荷变化，相比于传统控制，VSG控制的系统频率恢复的时间更短，频率波动幅值更小，证明了本文所提VSG控制算法的优异性。

4 结论

本文提出的基于算法优化的VSG控制策略，不仅实现了虚拟同步发电机的功能，并且通过运用改进蚁狮算法对控制策略参数进行优化，使控制器性能达到最佳。建立电力系统仿真模型并进行对比测试以验证本文所提VSG控制策略的控制性能，结果显示：基于改进蚁狮算法优化的VSG控制策略增加了系统惯性和频率稳定性，使得系统频率偏移的幅度和时间都显著降低，频率偏移幅度在阶跃负荷扰动下降低了约0.000 42 Hz，偏移时间降低了约1.5 s，在随机负荷扰动下偏移幅度降低了约0.000 13 Hz，偏移时间降低了约2 s，证明了频率协调控制策略的优异性能，解决了可再生能源电力系统惯性低、频率稳定性差的问题，可促进清洁能源的应用和可持续发展。未来，将进一步研究VSG在系统电压稳定性方面的作用，以完善VSG控制策略。