基于正交试验法整定主动悬架PID控制器参数

张裕晨，高坤明，路艳玲，郭宗和，马驰骋

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255049；2.莱芜职业技术学院 机械与汽车工程系，山东 莱芜 271100)

PID算法凭借其结构简单易实现、良好稳定性、工作可靠等优点在过程控制应用领域有广泛的应用[1]，但基于PID控制策略设计的控制器，其控制品质很大程度上受控制参数的影响，因而优化控制参数对于提升PID控制器的控制品质尤为重要。

常见的PID控制器参数整定方法包括：遗传算法、经验整定、Ziegler-Nichols公式、BP神经网络整定、内模整定、增益与相位裕度整定、PSO最优化整定等方法[2]。但实践中有些参数整定的方法不能应用于复杂模型，由于整定过程复杂、要求条件苛刻等因素的影响，使操作人员实际操作中只能凭借经验与凑试的方法调试PID控制器参数，整定的过程和结果受人为主观因素的影响较大，缺乏严谨性[3]。

本文搭建基于PID控制策略的1/4主动悬架模型，运用正交试验法整定PID控制器参数，结合响应图分析轮胎动载荷的极差变化并寻取P参数的相对最优值和相对最优区间，对挖掘PID控制器的控制品质以及改善汽车平顺性能有一定意义。

1 悬架系统模型的建立

按照参数是否根据路面状况而改变，悬架系统分为被动悬架、半主动悬架和主动悬架[4]。其中，主动悬架是在被动悬架的结构基础上增加一个可实时为悬架提供主动控制力的作动器，以求能够最大程度减弱车身振动。

1.1 1/4汽车主动悬架模型的建立

为了方便研究，本文使用简化后的二自由度1/4主动悬架进行受力分析与建立数学模型。模型如图1所示，参数取值见表1。

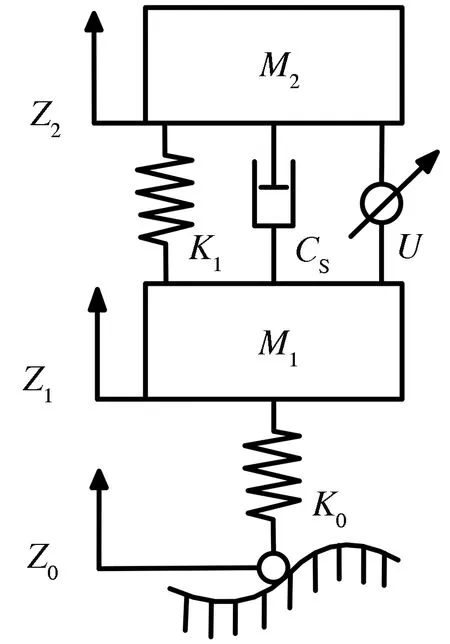
M1.簧下质量；M2.簧上质量；K0.轮胎等效刚度；K1.悬架等效刚度；CS.悬架等效阻尼；Z0.路面激励；Z1.簧下质量质心垂直位移；Z2.簧上质量质心垂直位移；U.作动器控制力。图1 主动悬架二自由度模型Fig.1 Active suspension model of two degree of freedom

表1 主动悬架模型参数取值Tab.1 The value of active suspension model parameters

根据牛顿第二定律，建立1/4汽车主动悬架系统动力学模型[5-6]：

K0(Z1-Z0)+U=0

(1)

U=0

(2)

将式(1)、式(2)整理后可得：

K0(Z1-Z0)-U]

(3)

(4)

依照式(3)、式(4)便可以在Matlab/Simulink中搭建1/4汽车主动悬架的子模型，如图2所示。

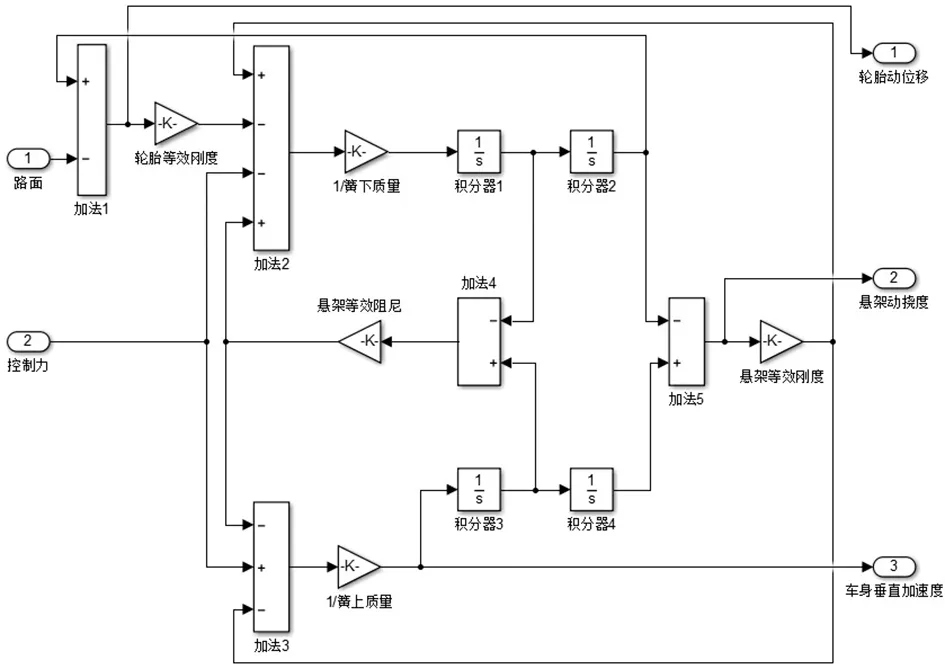
图2 1/4主动悬架子模型Fig.2 1/4 active suspension submodel

1.2 路面时域模型的建立

路面激励也称为路面不平度，指代路面的起伏变化程度或者相对于理想路面的偏离程度。同时，路面激励也是汽车在行驶过程中受到的主要激励，影响汽车的平顺性、动力性、舒适性等性能。

以滤波白噪声法模拟车辆经过特定等级路面时的情景更加真实、结果更加精确。所以，在利用Matlab/Simulink软件对主动悬架进行仿真实验中，普遍采用滤波白噪声法建立路面时域模型，以对路面不平度进行模拟[7]。

根据GB7031《车辆振动输入——路面平度表示》中所给出的标准，路面功率谱密度Gq(n)应为

(5)

式中：Gq(n0)为路面不平度系数；n0为参考空间频率；n为空间频率；w为频率指数。

常用的滤波白噪声路面不平度时域模型的表达式为

(6)

式中：n1为路面不平度下截止空间频率；u为行驶车速；Zg(t)为路面不平度位移；ω(t)为单位强度为1的高斯白噪声，无量纲常数。

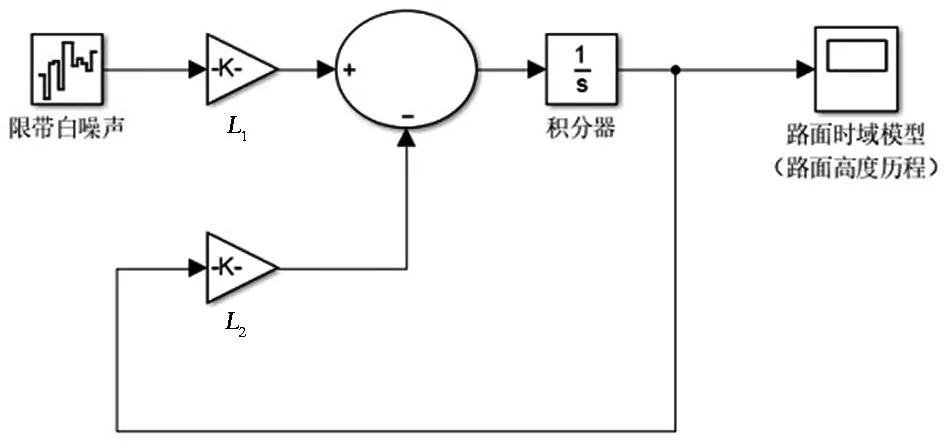
图3 C级路面时域模型Fig.3 C-level pavement time domain model

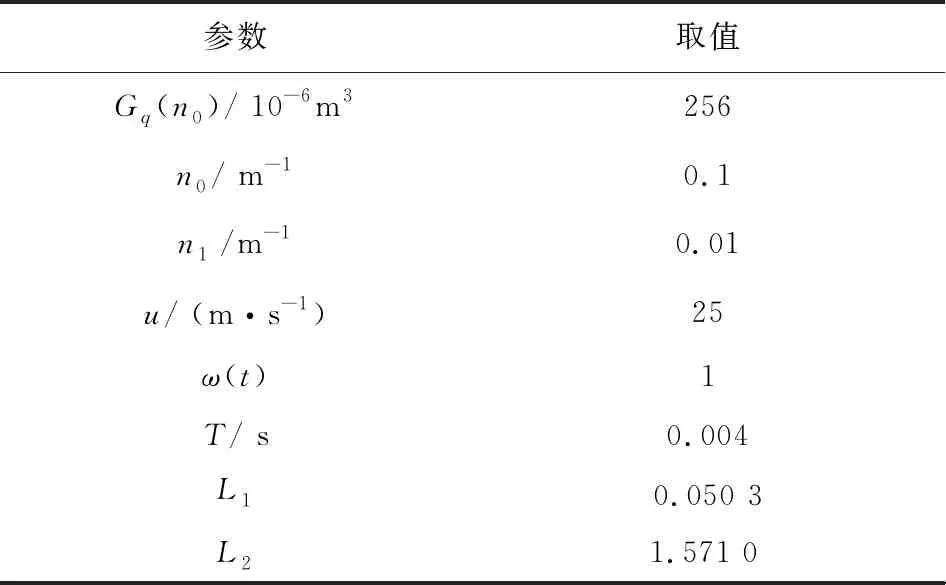
表2 C级路面时域模型参数Tab.2 C-level pavement time domain model parameters

若设路面时域模型的仿真时间为40 s,即车辆的行程为1 000 m，则仿真结果如图4所示。

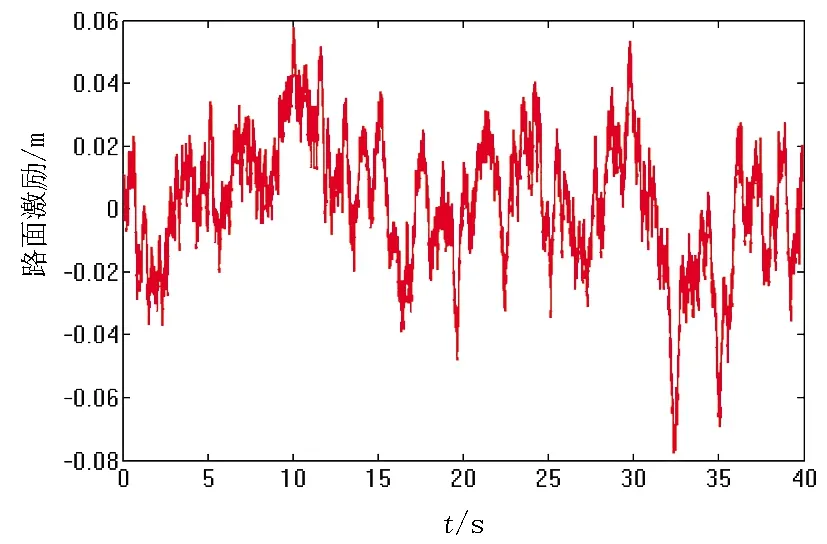
图4 C级路面激励Fig.4 C-level road undulate

1.3 1/4汽车主动悬架控制模型的建立

建立路面时域模型后，与主动悬架仿真模型以及PID控制器相结合，便可以得到用于试验的主动悬架控制模型[5]，如图5所示。

2 PID控制器的参数整定

PID控制中一个至关重要的问题是控制器参数的整定。整定的好坏不但会影响控制器的质量，而且还会影响控制器的鲁棒性。因此，对于PID控制器参数的整定也是对PID控制器的控制结果及控制品质的优化。

2.1 PID算法简介

PID算法具体分为P(比例)、I(积分)和D(微分)三项环节，控制系统可以通过调节系数提升调节性能，实现系统功能[9]。

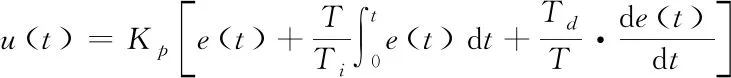
(7)

式中：u(t)为控制系统的输出；Т为控制系统采样周期；e(t)为控制系统的输入；Td为控制系统的微分时间；Kp为控制系统的比例系数；Ti为控制系统的积分时间。

2.2 正交试验法简介

正交试验法是通过设计排列整齐的分析表对试验进行整体设计、综合比较以及结果统计，通过较少的试验次数，达到分析出正确结论、得到较好结果的一种数据分析方法。正交试验包括两个重要部分：一是设计试验；二是结果的统计分析，即绘制正交试验结果分析表。

2.3 正交试验法整定PID参数的应用与实现

金波等[10]提出了一种基于正交试验整定PID参数的方法，通过建立水轮机模型且以缩小水轮机振动频率极差作为优化目标，取得了试验的成功。支龙[11]、Ammar 等[12]在论证主动悬架对于乘员舒适性的影响时指出，减小轮胎动载荷的波动范围能够有效降低车身振动频率，从而提升乘员的乘坐舒适性与汽车的平顺性。

轮胎动载荷在上下阈值范围内波动，所以，减小轮胎动载荷的波动范围也是减小轮胎动载荷上下阈值的差值，即减小轮胎动载荷的极差。本文在总结金波、支龙等学者研究成果的基础上，以金波提出的正交试验法思路为依据，以降低轮胎动载荷的波动范围极差为目的，设计PID控制器参数整定的正交试验。

2.4 极差分析法与设计正交试验

正交试验法整定PID控制器参数的前提需要对正交试验进行合理的设计与结果分析。极差分析法是正交试验结果的常见分析方式，能够有效地呈现出参数的优化方向，进而帮助设计者得到相对最优的参数。遵循先比例、之后积分、最后微分的原则对三个参数依次进行整定[4]，整定工作完成后，可将比例(P)、积分(I)、微分(D)三个参数的最优值作为组合运用到PID控制器中。

表3为用于判定每组最优参数的正交试验样表，以轮胎动载荷的极差值为标准，通过表4进行极差比较，将极差值最小的水平参数作为本组列的最优参数值代入下一组列继续进行试验。表3、表4中，j={1，2，3}，i={1，2，3，4，…，n}，Kij表示第i组列的第j项水平参数，Ri表示第i组列出现的最小极差，其所对应的水平参数为本组列的最优参数。

表3 正交试验样表Tab.3 Orthogonal test sampleTable

表4 轮胎动载荷极差分析样表Tab.4 Extreme difference analysisTable of tire dynamic load

注：极差=上阈值-下阈值。

本文以调节P参数为例，说明正交试验法整定参数的过程。首先，选取常数A，并令K11=3A,K12=2A,K13=A作为第一组列的三个水平参数进行试验。若最优参数为K1j，则第二组列的三个水平参数以K1j作为K22，K21=K22-A/2，K23=K22+A/2继续进行试验。

即以上一轮试验的最优水平参数为中心,同时两边各偏移上一组列各水平参数之间差值的一半作为本轮组列的三个水平参数[10]。例：若第n组最优参数为Knj，则第n+1组的三个水平参数为{Knj-A/(2n)，Knj，Knj+A/(2n)}。当连续三个组列的最优参数不再发生变化或者出现满意结果时，试验结束并以此参数作为PID控制器的最优控制参数。

关于常数A的取值，可以根据经验自定。但本文认为，常数A的取值不应过小，这样可以扩大被整定参数的取值范围，有利于获取最优参数。

3 试验与结果分析

作为最先进行整定的P参数，在对P参数进行整定时将I参数和D参数的值均设为0，同时设常数A的取值为4 096(211)，试验结果保留小数点后一位有效数字。经过11轮仿真试验以及对每组的试验结果进行分析后，整定出了[64,12 288]区间内P参数的最优取值及最优区间。但文中所设计的正交试验无法验证实际最优参数是否会存在于[64,12 288]区间之外，所以本次正交试验所寻取的参数为相对最优参数而非绝对最优参数，最优区间为相对最优区间而非绝对最优区间。

3.1 相对最优值的确定

依照本文第2.3节记述的步骤进行正交试验，并将数据记录后绘制成正交试验表(见表5)，即P参数的试验方案与结果表[13]。

分析表5可以得出，水平参数处于较大值时，随着轮胎动载荷极差的降低，每个组列的最优参数相比于上一组列也呈现出不断减小的趋势。但随着试验的进行，最优参数的取值并不完全随着轮胎动载荷极差的降低而减小。

通过对比第9组、第10组、第11组正交试验所得出的最优参数可以看出，第9组、第10组、第11组正交试验的最优参数均为176，所对应轮胎动载荷的极差为1 916.6 N。依照本文2.4节所述，当出现连续三个组列的最优参数不再发生变化时，则以此参数作为PID控制器的控制参数，即PID控制器的P参数相对最优取值为176。

表5 正交试验表Tab.5 Orthogonal testTable

3.2 仿真结果比较

通过正交试验法，对主动悬架PID控制器的P参数进行了整定,图6为初始参数P=4 096与整定后的P=176时的轮胎动载荷响应对比。

图6 PID控制的轮胎动载荷响应图Fig.6 The dynamic load test results of tires of PID control

由表5的数据记录和图6的曲线对比可以看出，在相同的外部条下，轮胎动载荷极差大致上随P参数的降低而降低，直至P=176时轮胎动载荷的极差值为最低。P=4 096时轮胎动载荷的上阈值为1 520.2 N，P=176时轮胎动载荷的上阈值降低到了1 006.5 N，降低了33.79% ；P=4 096时轮胎动载荷的下阈值为-1 702.1 N，P=176时轮胎动载荷的下阈值增加到了-910.1 N，增加了46.53%；P=4 096时轮胎动载荷的极差值为3 222.3 N，P=176时轮胎动载荷的极差值降到了1 916.6 N，降低了40.52%，达到了通过整定PID控制器参数提高汽车平顺性的目的。

3.3 相对最优区间

可在各组列中选取与最优参数下的轮胎动载荷极差差值最小的两个水平参数作为相对最优区间的端点，同时相对最优区间要包含相对最优参数在内。

通过对极差分析表的分析，可以进一步得出参数的相对最优区间，便于为在实际应用中提供更多的选择和参考。表6、表7、表8分别列举出了第9组、第10组、第11组正交试验中各组列水平参数对应的极差值。

表6 第9组正交试验极差分析表Tab.6 Range analysisTable of the 9th group orthogonal test

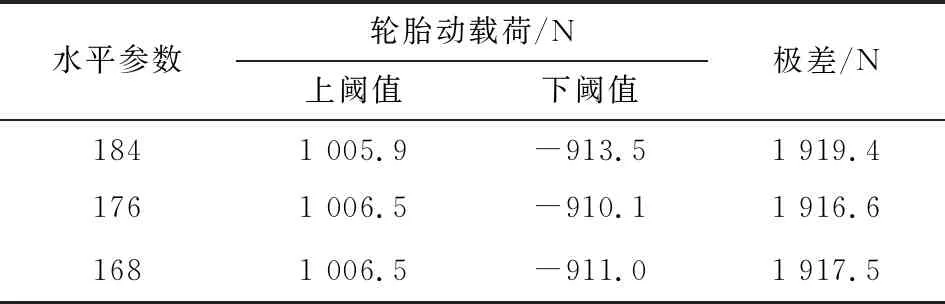
表7 第10组正交试验极差分析表Tab.7 Range analysisTable of the 10th group orthogonal test

表8 第11组正交试验极差分析表Tab.8 Range analysisTable of the 11th group orthogonal test

从上述3个表格可以得出，与最优参数176的极差相差最小的两个水平参数分别为第11组正交试验的水平参数180(与相对最优参数176的极差相差1.4 N)和水平参数172(与相对最优参数的极差相差0.8 N)，且172<176<180，由此可以认定，PID控制器的P参数取值的相对最优区间为p∈(172,180)。图7为第11组正交试验各水平参数仿真结果。

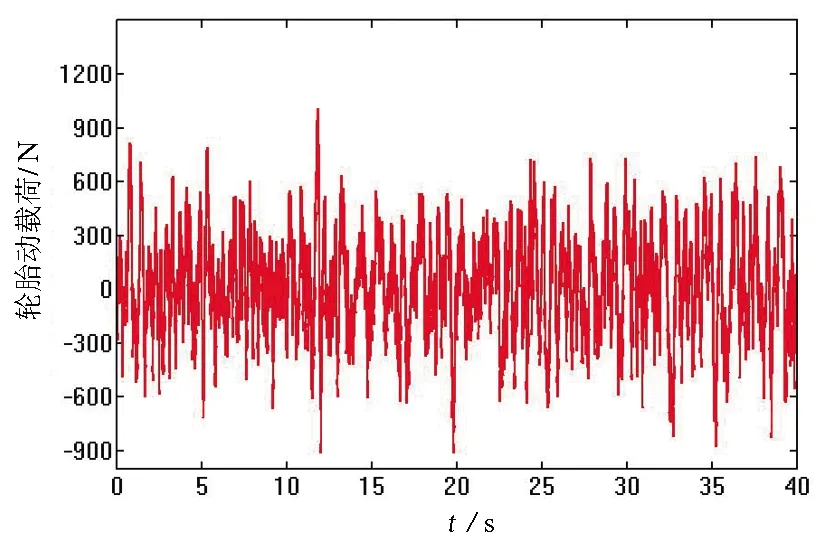
(a)水平参数P=180

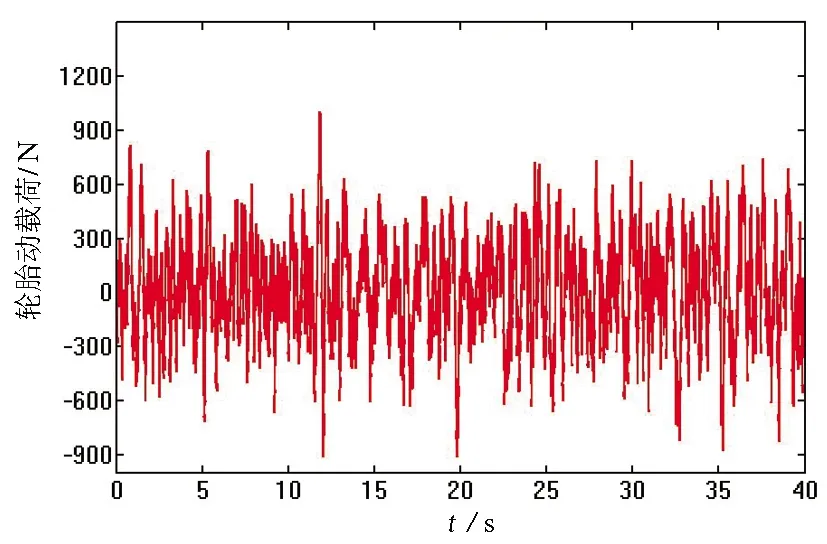
(b)水平参数P=176

(c)水平参数P=172图7 第11组正交试验各水平参数下的轮胎动载荷结果图Fig.7 The dynamic load test results of tires under the horizontal parameters of the 11th group orthogonal test

由图7可见，进行到第11组正交试验时，P=176时轮胎动载荷的上阈值、下阈值、极差均小于P=172以及P=180时的轮胎动载荷的上阈值、下阈值、极差，且各水平参数之间的轮胎动载荷上阈值、下阈值、极差相差极小，由仿真试验再次验证，P=176为主动悬架PID控制器的最优参数，P∈(172，180)为PID控制器P参数取值的最优区间。

4 结束语

1)关于PID控制器I(积分)、D(微分)的参数整定亦可使用正交试验法进行，本文不再赘述。特别注意的是，在进行某一参数整定的过程中，对于其他尚未整定的参数应将其数值设为0，而对于已经整定过的参数值则无需变动。

2)正交试验法的实现形式多种多样，汽车平顺性能的评价指标也不为单一。在选择优化目标时，要考虑不同目标间存在的相辅或相冲突的关系，以便于更加科学地设计正交试验。

3)本文旨在研究与验证正交试验法用于主动悬架PID控制器参数整定的有效性，依靠Matlab/Simulink建立主动悬架模型，通过设计并进行试验，给出了该方法可行性的论证。