基于属性更新的MSP数据访问控制机制
韩 刚,庞 龙,罗 维,王浩琛
(西安邮电大学 网络空间安全学院,陕西 西安 710121)
集中式计算通过基础中央处理器向访问者提供服务,维护简单,并且可直接与数据库相连接,有效地保护了数据库的安全[1]。但是,集中式储存数据库需求中央处理器性能较高,当访问者访问数量过载时,可能会导致中央处理器响应速度过慢或死机。随着访问者对于访问速度需求的提高,集中式计算逐渐被分布式计算替代。分布式计算提供多个智能终端,主要为访问者提供资源分配、云计算等服务[2],分散处理任务降低了处理器的任务量,访问速度也有所提高,现已广泛应用在对响应速度要求较高的智慧医疗、人工智能等领域[3]。
在分布式计算中,主机处理的大多是其内部任务,而加解密计算任务是由智能终端去完成[4],但各终端的安全防护较低,在网络中往往存在一些安全问题,如面对分布式拒绝服务、局域网地址洪泛等攻击方式[5]。在密文策略属性基加密系统(Ciphertext Policy Attribute based Encryption,CP-ABE)加密过程中,面对访问者属性以及访问者密钥的更新对于各个终端的可管理性以及灵活性也要求较高[6]。在已有的相关研究中,储存局域网(Storage Area Network,SAN)技术集中存储方案虽然提高了存储系统的资源利用率和系统扩展性,但在安全问题上仍然存在一定隐患[7]。随着密码学相关知识的提出,数据的安全性也得到了保证[8]。基于部分跨级和集中存储模式的库存配置与选址决策模型虽然提高了系统存储的安全性,但系统性能还有待提高[9]。云存储应用中的加密存储及其检索技术对于数据实现了基本加密,提高了存储信息的性能[10]。基于拉格朗日多项式插值法的密钥产生方案,利用拉格朗日插值法,实现了密钥的分配管理,但对系统的性能要求较高[11]。基于对称布尔函数算术也为数据的安全性提供了一定的保证[12]。减低系统性能需求、支持关键字的可搜索加密方案通过陷门关键字实现了一次双线性对计算搜索关键字[13]。将CP-ABE用于加密,同时使用云计算外包服务,加入访问者属性,可提高系统的安全性[14]。利用雾计算方法,将复杂的计算交给外包雾节点,提高了计算的高效性与可靠性[15]。在雾计算中设计访问者和属性可撤销的方案,通过雾节点外包计算,降低中央服务器的性能需求,实现了属性撤销[16]。雾计算中细粒度属性更新的外包计算访问控制方案,给雾节点降低了访问者加解密开销[17]。利用云计算进行数据加密,将可搜索加密用于保存数据,提高了保密性以及可用性[18]。然而,上述方案虽然解决了计算性能的需求问题,但在数据统一管理与安全性方面均存在一定的缺陷。
为解决上述问题,建立一种基于属性更新的MSP数据访问控制机制。构建集中式计算与分布式计算相结合的网络分布模式,通过区域处理器对于每一个区域的访问者进行管理,且只能通过中央处理器访问数据库。同时,实现基于密文策略的CP-ABE加密,在访问者端通过公钥加密方式加密明文,发送至区域处理器,通过区域处理器对访问者进行管理,建立组密钥二叉树所生成的组密钥,对于密文进行重加密并发送至数据库存储。最后,通过区域处理器与区域授权中心(Apartment Authorization,AA)之间进行访问者属性组的信息的交互,实现更改访问者属性的更新与撤销。
1 相关理论知识
1.1 访问控制树
访问控制树用于隐藏源数据的加密密钥。令根节点为r,建立访问控制树R。该访问控制树指定了在解密密文时需要的属性组合,R树中的每个内部节点都是逻辑运算符,如“AND”“OR”。每个叶子节点表示一种属性。属性可以是定义、分类或注释访问者的任何描述性字符串。根据秘密共享的思想,访问控制树的每个节点表示一个秘密,在加密阶段需要自顶而下为每个节点分配一个秘密。在解密阶段则需自下而上回复根节点的秘密。
1.2 拉格朗日插值算法
对于任意t-1次多项式[19]
y(x)=at-1xt-1+at-2xt-2+…+a1x+K
(1)
常数项K∈P[x]为需要保护的密钥。如果存在y(xi)使得t个点xi都在y(xi)上,则可确定y(xi)的系数ai,0≤i≤t。令a0作为密钥,使用两个以上的密钥片段Si,可产生公钥KP=a0,若有n个密钥片段,则可产生多个密钥Ki。随机选取r个密钥片段(r≤n),即可产生密钥总数为
故当一个访问者拥有r个密码片段Si而非n个密钥Ki时,等价于拥有A个密钥。当n>2时,根据拉格朗日插值多项式
其中:x为有限域p[x]中的整数;kml为第m个密钥片段在l域中的安全系数;xml和xmj分别为在l域和j域中访问者所对应的第m个密钥片段。若存在素数P∈P[x],且P的值大于n和K,引入模运算,多项式可表示为
其中,所选择的素数P以及多项式f(x)均由AA管理。
1.3 双线性映射
令G1和G2为两个素数阶数为h的乘法循环群,且g为子群,若满足以下两种属性,则映射e:G1×G1→G2为双线性映射[20]。
1)双线性。对于任意的w,v∈G1,a,b∈P[x],存在e(wa,vb)=e(w,v)ab。
2)非简并性。G1中存在子群g0,使得e(g0,g0)≠1成立,且满足
e(wa,vb)=e(w,v)ab-e(wb,va)。
1.4 决策双线性
决策双线性Diffie-Hellman[21](Decision Bilinear Diffie-Hellman,DBDH)问题的定义为挑战者根据安全参数选择一组阶为素数P的G1。将g作为生成元,选取随机数a,b,s,∈P[x],假设挑战者已知(g,ga,gb,gs),则有效元组e(g,g)abs∈G1。即对于挑战者而言,很难区分有效元组e(g,g)abs∈G1与密钥K∈G1。
以优势Q解决DBDH问题,即满足
{Pr[(g,ga,gb,gs,e(g,g)abs)=0]-
Pr[B(g,ga,gb,gs,K)=0]}≥Q
若优势Q可忽略不计,则DBDH问题假设成立,即挑战者无法区分有效元组和密钥。
2 MSP数据访问控制机制
2.1 机制模型
MSP数据访问控制机制主要由云服务商(Cloud Service Provider,CSP)、中间服务商(Middle Service Provider,MSP)、中央权威机构(Center Authority,CA)、属性授权机构(Property Authority,PA)、数据拥有者(Data Ower,DO)和数据访问者(Data User,DU)等6部分组成。将一个大区域分散为若干个小区域,并对每个小区域分配区域处理器,区域处理器负责控制管理每一个区域中的访问者集合。机制模型如图1所示。

图1 机制模型
CSP主要负责存储拥有者所上传的信息,实现数据的集中化存储,假设CSP为半可信机构。MSP负责建立访问控制树,CSP与数据访问者通过MSP建立信息交互通道,同时完成信息的重加密解密,同样假设MSP为半可信机构。CA是在机制中完全受信任的一方,统一发放机制中的密钥与主密钥。PA通过CA所发放的密钥以及访问者的属性集产生的私钥,并负责私钥的分发与撤销。DO一般将自身已加密的信息,通过MSP重加密,再上传至CSP完成存储。DU向MSP发送访问请求,并且符合身份认证之后,才能获得存储在CSP的拥有者的密文信息。
2.2 机制结构
MSP数据访问控制机制结构分为机制初始化、密钥生成、数据加密、组密钥生成、密文重加密、私钥更新和密文解密等7个过程。
1)初始化Setup(1k,L)→KP,KTS。将安全系数k与属性集合L作为参数,进而获得整个机制的公钥KP与主密钥KTS。
2)密钥生成AAkeyGen(KTS,u)→KS。通过输入主密钥KTS以及访问者所拥有的属性u,u∈L,计算出私钥KS并发给访问者。
3)数据加密。数据拥有者发送数据之前,通过随机密钥KC结合访问控制数R对信息M进行加密,之后由MSP运用加密算法结合随机密钥KC进行秘密共享加密,共分为两个子算法,即DO在本地运行DO.encrypt和MSP在服务器端运行MSP.encrypt。
DO.encrypt(KP,KC,M)→C1。将公钥KP、随机向量v、信息M以及随机密钥KC作为输入通过秘密共享算法加密,输出密文C1并发送给MSP。
MSP.encrypt(R,KP,C1)→C。将公钥KP访问控制树R作为输入,得到加密之后的密文C,建立与访问者之间的数据通道。
4)组密钥生成GkeyGen(KTS,u)。将主密钥KTS与属性u作为输入,通过拉格朗日插值法迭代,建立二叉树得到组密钥KGb,1≤b≤u。
5)重加密reEncrypt(KGb,C)→Cr。MSP接受到访问者发送的密文C之后,结合生成的组密钥KGb进行加密运算,得到密文C2,再通过数据加密标准(Data Encryption Standard,DES)加密,得到重加密密文Cr。
3 身份认证与数据加密
数据传输过程中大多数机制无法实现访问者信息的统一管理及加密,因此,在CSP与访问者之间建立数据访问控制模型,如图2所示。
图2中,首先,通过MSP在数据访问者与CSP之间建立数据访问通道,以实现对访问者数据的统一管理。其次,利用MSP建立访问控制树,采用拉格朗日插值法迭代,形成具有访问者属性的访问控制树。最后,通过组密钥的更新实现访问者属性的撤销与更新。
3.1 密钥初始化
令G1和G2为两个以P为模数的可循环乘积群,g可生成循环群G,则产生T:{0,1}*→G1和T1:G2→P[x]两种定义。
CA选择一组随机元素{z0,z1,z2,…,zn}∈G1,选取访问者所对应的zu,并授予信任属性φ(u),生成公钥KP={e(g,g)z0,z1,z2,…,zn∈G1,φ(u)}。选取随机参数q∈P[x],结合属性集合L,生成主密钥KTS=(gq,L)。
3.2 私钥生成
由区域授权中心AA运行私钥生成。以主密钥KTS与访问者属性u作为输入,同时DO生成随机向量v,选取随机数r,ε∈P[x],选取r1,r2使得r1和r2在模r上同余,将r作为访问者所分配的随机密钥,则私钥为
KS={gε,gεr,gr1+r2,gv},r1(modr)=r2(modr)
3.3 数据加密
数据加密分为两个阶段。
阶段1DO向MSP传输数据之前,先进行一次加密,即DO.encrypt。将访问者数据上传至MSP之前,访问控制树R、公钥KP和KS关联的双线性秘密共享方案为(S,T)。将信息M作为参数输入,DO输出密文
C1={(S,T),Me(g,g)z0S,gS,gz0S,gqv}
阶段2MSP在收到访问者数据后,结合属性集合L,建立访问控制树R,如图3所示。

图3 访问控制树
选取随机参数P∈P[x],根据式(1),结合访问者的属性u,生成根节点的多项式为
E(x)=a1xn+a2xn-1+…+u(modP)
(2)
给根节点赋值B,求解式(2),得到子节点的值,其他未赋值的子节点采用迭代方法为其赋值。若子结点处的运算符为AND,计算不同子节点的值,其代表访问者所拥有的属性秘密值。若子结点处的运算符为OR,使子节点的值对应的属性符合访问控制树,且满足访问者的属性集合。
3.4 组密钥的生成
根据访问控制二叉树的建立,每个访问者节点值均由MSP计算生成。每个子节点的属性标识符属于二叉树每层生成的属性标识符,从叶子节点到根节点通过的节点为路径节点,在每个路径节点处存储该节点的密钥,且定义一个属性公开参数δi∈P[x],根据访问者所对应的属性组,找到含有访问者组属性得覆盖子树,从而建立组密钥KGb=(ω1,ω2,…,ωb),b为用户的属性个数,通过设置(S,2)秘密共享方案,采用拉格朗日插值法计算KGb。属性组密钥二叉树如图4所示。

图4 属性组密钥二叉树
假设访问者组属性为(u11,u21,u33),则在二叉树所对应的节点为[ω21,ω33],生成的组密钥为KGb=[ω21,ω33‖δ1],由此得到密文
C2={(S,T),Me(g,g)z0S,gS,gz0S,gqvKGb}
3.5 密文重加密
MSP接收到由DU发送过来的C2,对C2进行DES对称加密实现密文的重加密,则输出的重加密密文为
Cr=E(C2⊕v)
其中,E(·)表示DES对称加密。
3.6 私钥更新
当MSP收到DU所发送的请求时,根据MSP的组密钥二叉树规则,将新建节点所经过的层数发送给访问者。设所建立二叉树的秘密共享方案为(S,2),因此只需要知道两个部分即可推算出组密钥KGb,由于δ是公开参数,所以只要访问者的属性属于该属性组的子集,则可计算KGb。DU利用KGb计算更新之后的私钥为
3.7 密文解密
DU发送请求之后,CSP返回密文,并进行解密,数据加解密过程如图5所示。
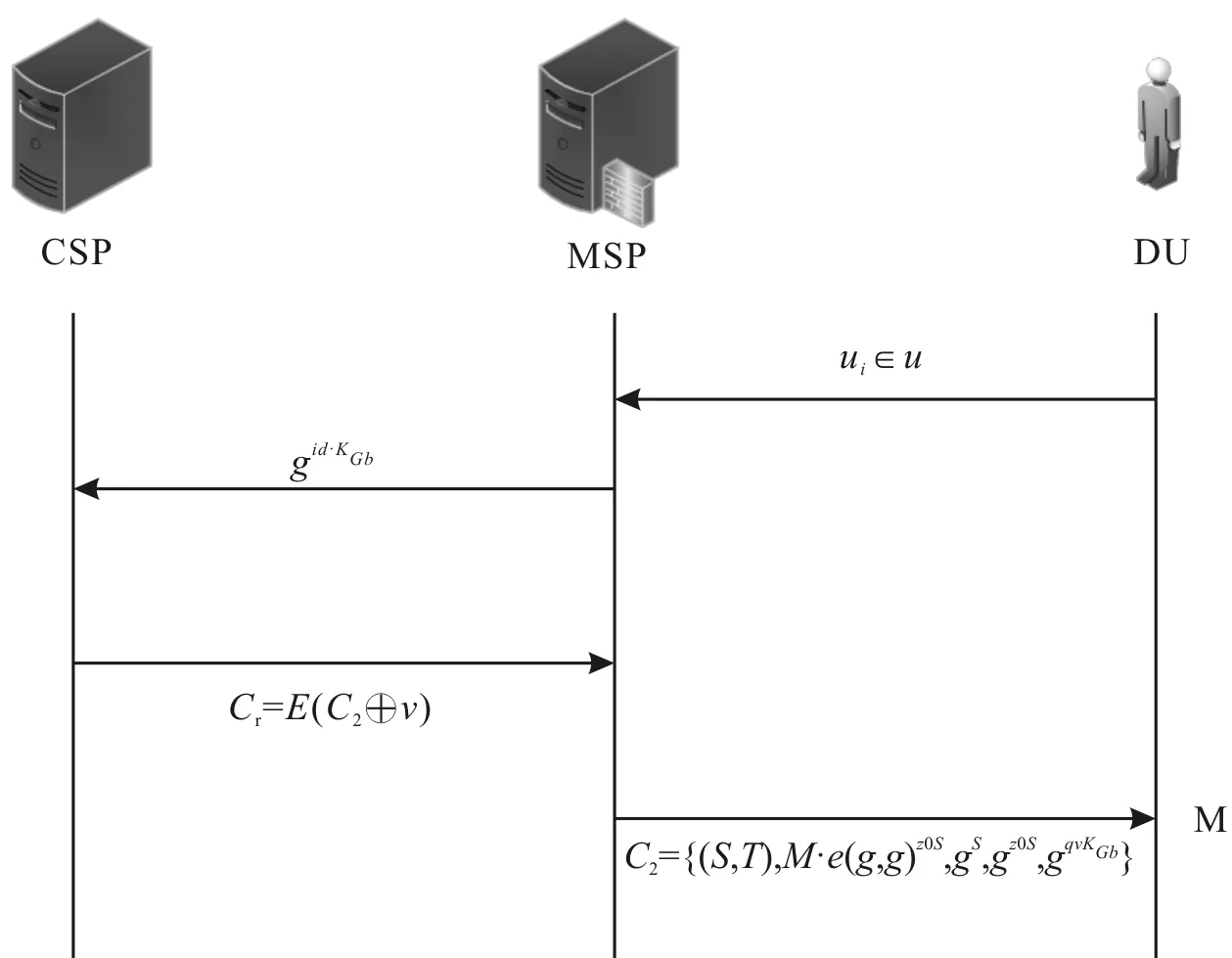
图5 数据加解密过程


DU结合密文C2,得到明文
4 性能分析
4.1 理论分析
所提机制与文献[4]、文献[6]和文献[7]等4种方案的计算开销对比如表1所示。表1中:c表示在G1群中的一次幂运算;d表示在G2群中的一次幂运算;e表示一次双线性运算;ρ为密文被加密算法的时间复杂度;×表示没有进行该运算。一般在构造具有双线性对算法时,采取的嵌入次数为2或者3,此时的ξ远大于c和d,k>1可认为在一次加密过程中,数据加密时间复杂度远大于属性更新。

表1 不同方案的计算开销对比
文献[4]方案在运算的过程中,加密方式采取同态加密算法,该机制使用两个不同的多项表达式,故加密算法所需要的时间复杂度为O(ρ2),远高于所提机制采用双线性映射的时间复杂度,并且缺乏属性更新功能,系统整体的可使用性不强。文献[6]方案在运算过程中其外包加密以及解密的过程外包给了雾节点,利用随机数以及访问者秘密数进行加解密,且不涉及属性更新,因此并不需要进行过多的线性计算,故外包加密与解密的复杂度较小,但由于数据拥有者需要对于数据进行Owner.Enc算法,因此所需要的时间复杂度较高为O(ρlogρ),较时间复杂度来说,所提机制更具有优势。文献[7]方案在外包加密步骤分为两个阶段,需要从属性机构执行加密并进行两次访问控制树的递归遍历,保证数据的安全性以及访问者身份的访问控制,运算复杂度高,故对于外包加密解密的时间复杂度上来说,所提机制也具有较大的优势。
从理论分析结果来看,所提机制与其他3种方案在数据加解密的时间消耗方面不同,所提机制只进行了一次控制树的遍历,在外包计算方面的效率具有较大优势,且在外包加密上建立访问控制树结合属性加密又保证了数据的安全性。
4.2 实验分析
在charm-crypto框架内进行仿真实验,使用英特尔i5-8250U 1.80 GHz处理器,8 GB内存,搭配环境为Ubuntu 18.04.1,64位系统与Python3.9。将所提机制与其他3种方案分别从加解密时间和外包加解密时间两个方面进行对比分析,结果分别如图6和图7所示。实验所有结果均是10次结果的平均值。
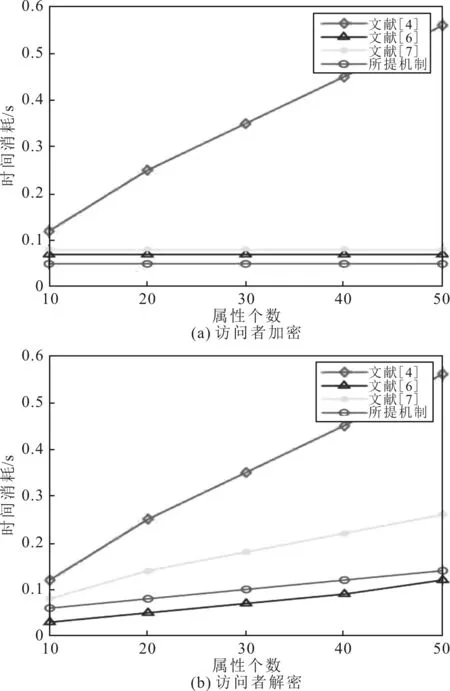
图6 不同方案访问者加解密时间对比

图7 不同方案外包加解密时间对比
由图6可以看出,所提机制与其他3种方案的加解密时间不同。由于文献[4]方案没有外包加解密机制,故加解密随着访问者个数的增加其上升速度远大于其他3种方案。文献[6]方案与文献[7]方案在加密的时间消耗较大,而所提机制的加解密时间消耗最小,具有一定的优越性。所提机制将复杂的计算外包出去,提高了访问者加密效率,且加密的时间基本恒定。
由图7可以看出,随着属性数量的增加,所提机制与文献[6]方案、文献[7]方案的时间消耗均会呈线性增长的趋势,故外包加密的时间也会随属性个数的增加变长。图7(a)中,所提机制产生的时间消耗较小,这是因为采用门限法生成密钥在密文的重加密阶段减少了大量的损耗。图7(b)中,所提机制使用MSP控制整个区域,在解密过程中消耗的资源较少,故所提机制在外包加解密时效率更高。
5 结语
基于属性更新的MSP数据访问控制机制使用MSP控制并管理一个区域的数据信息,同时进行加密及解密处理,在保证需求的前提下完成属性更新,确保了数据的安全性。理论分析与仿真实验结果表明,当访问者的属性个数较大时,在该机制下进行信息加解密的时间开销较小,加解密效率高,同时,在外包加密上建立访问控制树结合属性加密又保证了数据的安全性。

