一种低电压VCO-ADC的设计与校准方法
佟星元,杨 梅,郭 慧
(西安邮电大学 电子工程学院,陕西 西安 710121)
模数转换器(Analog-to-Digital Converter, ADC)是连接模拟域和数字域的“桥梁”[1],是片上系统(System-on-Chip, SoC)中必不可少的组成部分。常见的ADC在模拟域完成数字量化[2]。随着集成电路工艺特征尺寸的不断缩小和晶体管特征频率的不断升高,数字电路的时钟频率得以提升。时钟频率的提高有利于增加时间域的分辨率。目前,越来越多的新兴应用领域需要ADC在低电源电压条件下工作。在低电源电压条件下,一方面,受限于比较器的精度,高性能ADC的设计变得更加困难[3];另一方面,模拟输入信号从模拟域直接量化成数字信号也变得越来越困难。因此,在低电压条件下,将信号从模拟域转换到时间域,在时间域内完成数字量化的方式广受关注。
基于压控振荡器(Voltage Control Oscillator, VCO)的ADC(VCO-ADC)是一种典型的时间域ADC[4]。VCO-ADC电路具有数字化程度较高,与电源电压演进的兼容性较好等优点,有利于ADC在低压下工作[5]。然而,由于VCO电压-频率特征曲线的非线性特征,导致VCO输出的正弦振荡波形存在谐波,从而影响整体ADC的性能,并且随着电源电压的降低和对精度要求的提高,非线性问题会变得更加严重。
虽然采用差分结构,可以有效抑制偶次谐波和共模干扰[6],但也只能在一定程度上改善线性度,很难实现高精度。针对VCO-ADC线性度较差的问题,一般有数字校准技术[7-9]、增加反馈环路[10]和多通道相位技术[11]等多种改善方法。其中,由于数字校准技术的电路数字化程度高,工艺移植性和电压演进的兼容性都较好。
采用最小均方根算法[12](Least Mean Squares, LMS)和Delta-Sigma ADC的数字背景线性化技术[13]能够改善非线性,但这两种方案均需要在较高电源电压下实现,且均需要模拟电路的支持,电路的面积和功耗较大,不适用于低压领域的应用。
考虑到低电压的工作条件以及电路面积和功耗能等指标,拟设计一款基于180 nm互补金属氧化物半导体(Complementary Metal Oxide Semiconductor, CMOS)工艺的12 bit 0.8 V VCO-ADC。VCO-ADC采用分裂ADC结构,包含两个VCO-ADC子通道。通过向子通道中加入扰动信号的方式来使输出中包含扰动信号信息,再使用基于查找表(Look-Up Table, LUT)的非线性数字校准算法对设计的ADC进行校准,以提高VCO-ADC的精度。
1 VCO-ADC的工作原理
VCO-ADC主要由压控振荡器、计数器、寄存器和减法器等模块构成。其中,VCO将电压域信号转换为时间域信息,输出的数字信号具有与输入信号相关的频率/周期信息,该数字信号作为计数器的计数时钟,在一个采样周期内完成计数,计数结果为与模拟输入对应的数字量。寄存器完成对计数器在转换周期内计数结果的存储。减法器对两个差分通道的计数结果求差,得到最终的数字输出。
设计的VCO-ADC由两个通道构成,其原理示意图如图1所示,其中,通道A和通道B由两个完全相同的差分VCO-ADC构成,每个差分VCO-ADC由两个完全相同的单端ADC构成。其工作原理为,Vn、Vp作为VCO-ADC的输入信号,通过VCO产生与之对应的输出信号,此信号将作为每个单端ADC中计数器的计数时钟,辅助计数器完成一个采样周期内的计数,计数器的输出作为减法器的输入,最终通过减法器得到差分VCO-ADC的数字输出nA、nB。

图1 VCO-ADC原理示意图
2 VCO-ADC设计及校准
2.1 VCO电路设计
设计的VCO电路为一个环形电路,其电路结构结构示意如图2所示。其工作原理为,当晶体管M7工作在饱和区时,可以将其近似当作一个压控电流源,实现电压到电流的转换。由M7、M8和M9构成的电流镜可以将输入控制电压Vin转换为电流Ictrl,并且电流Ictrl的大小由输入电压Vin控制,从而使得环形VCO输出频率的快慢也由输入电压Vin控制,即环形VCO能够完成从模拟输入电压Vin到时间域信号(频率)的转换。环形VCO在输入电压Vin的作用下,产生一段连续的正弦振荡信号Vosc,通过反相器可将该振荡信号转换为相应频率的脉冲信号VT[14]。

图2 环形VCO电路结构示意图
对于12位的全差分VCO-ADC,在一个转换周期内能够输出的最大值为4 095,因此ADC中计数器在一个转换周期内必须计数到4 095才能满足要求。设计的VCO-ADC为12位5 kS/s的采样率,经过计算,若要满足要求,VCO最大输出频率应该至少大于20.475 MHz。从电路的分辨率、线性度等方面进行综合考虑,最终确定VCO输出频率的范围为15~50 MHz。
2.2 计数器电路设计
计数器通常分为异步计数器和同步计数器两种。考虑到异步计数器在面积和功耗方面较同步计数器都具有明显优势[15],因此选用异步计数器来实现计数功能。在一个转换周期内,理想情况下的12位VCO-ADC中的VCO输出脉冲信号可以通过12位计数器完成计数,但是,通过仿真发现,VCO的输出频率范围为16.58~40.89 MHz,超出了12位计数器的计数范围,如果继续使用12位的计数器,会带来ADC输出码溢出的不良后果,为了防止这种情况的出现,采用13位加法计数器。13位计数器的电路结构示意图如图3所示,其中,VT为输入信号经过VCO输出的脉冲信号;作为计数器的计数时钟Vclk为ADC的时钟信号,其完成对计数器的复位。13位计数器舍弃最低位,剩余位作为单端ADC的数字输出依次为D11、D10、…、D0。
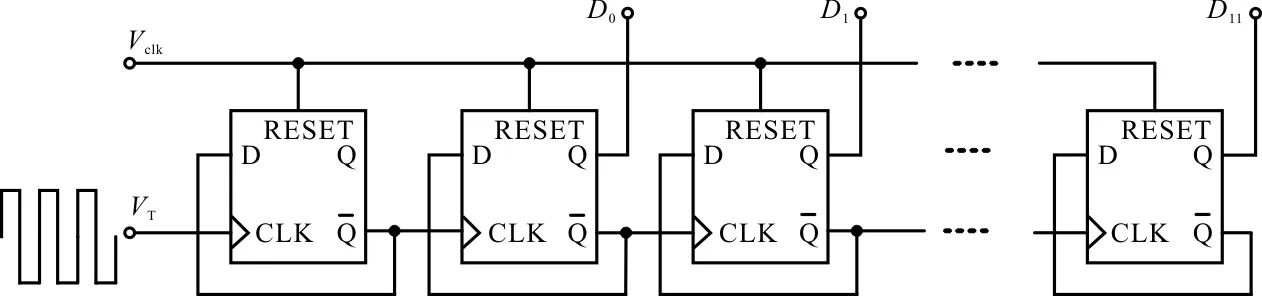
图3 加法计数器电路结构示意图
2.3 寄存器电路设计
作为一种逻辑记忆电路,寄存器具有暂时存储数据的功能[16]。在VCO-ADC的一个转换周期内,计数器会不断输出计数结果。只有当一个转换周期结束时,计数器的输出才为ADC的最终数字输出。寄存器的作用就是对数字输出进行暂时的存储,因此在计数器之后加入12位寄存器。在第n个转换周期的Vclk来临之前,寄存器存储计数器的输出,得到第n-1个转换周期内ADC的输出,完成一次模数转换。当第n个转换周期的Vclk来临时,寄存器保存第n-1个转换周期内的计数结果。在Vclk作用下,计数器复位,并且开始计数第n个转换周期内VCO的输出频率,以此类推,重复上述步骤,直到下个转换周期Vclk到来时,寄存器被复位,存储第n个转换周期内计数器的计数结果,实现对每个转换周期内数字输出码保存一个周期的功能。

图4 寄存器电路结构示意图
2.4 减法器电路设计
每个通道的VCO-ADC均采用差分的形式进行设计,每个通道的两端输入Vn、Vp通过ADC得到数字输出码nA、nB之后,通过12位减法器对数字输出码进行处理,实现差分功能,得到VCO-ADC的最终输出Dout。
12位减法器中Vclk为时钟信号,Ai、Bi分别为计数器A、B的第i位通过寄存器A、B之后的保存值,作为减法器的输入信号。Li-1为第i-2向第i-1位的借位值,即低位向本位借位的值,Li为第i位向第i+1位的借位值,即本位向高位借位的值,Si为第i位减法器的输出值[17]。单端ADC的输出都会随输入的变化而变化,所以减法器的输出也是变化的。当输入Vn小于Vp时,Ai、Bi相减得到负数,而减法器并没有分辨正负数的功能,所以最高位S11的结果由第12位减法器的借位输出信号与VDD经过异或门的结果决定,最终得到S11。12位二进制减法器的电路结构示意图如图5所示。
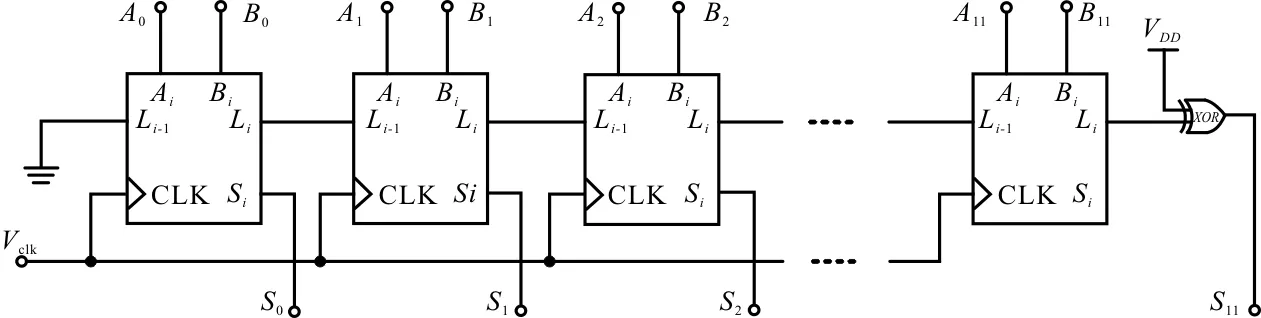
图5 减法器电路结构示意图
3 仿真结果与分析
3.1 各模块仿真
3.1.1 环形VCO仿真
环形VCO的周期稳态(Periodic Stead State, PSS)电压/频率特性的仿真结果如图6所示。可以看出,环形VCO的电压输入范围为0.54~0.76 V。在整个输入电压范围内,输出频率随输入电压的增大而变快,仿真得到的输出频率范围为16.58~40.89 MHz,大于至少需要达到的输出频率。

图6 环形VCO的电压/频率特性曲线
3.1.2 计数器电路仿真
设计VCO-ADC的采样率为5 kS/s,即采样周期为200 μs,给定VT为一个1 μs的脉冲信号,设定Vclk为200 μs。异步加法计数器电路的仿真结果如图7所示。可以看出,在每个采样周期内,13位计数器的理想结果本应为199,经过舍弃最低位的值之后,得到计数器的最终结果为99。

图7 异步加法计数器电路的仿真结果
3.1.3 寄存器电路仿真
寄存器在采样点处对计数器的输出进行存储,并对计数结果完成一个周期的保存。将计数器电路与寄存器电路相连之后,寄存器电路的仿真结果如图8所示。图中的D11、D10、…、D0分别为计数器各个位的输出,Dout为计数器对VCO的输出信号计数的结果,即ADC的数字输出。

图8 寄存器电路的仿真结果
从图中8可以看出,在0时刻,计数器的输出为0,寄存器保存了此时计数器的输出结果,并在0 μs~200 μs这个采样周期内输出0,在下一个采样时钟来临时,计数器完成复位并开始重新计数,寄存器输出并保存了输出结果。
3.1.4 减法器电路设计
将寄存器与减法器相连之后减法器电路的仿真结果如图9所示。其中,D11、D10、…、D0分别为减法器的12位输出,DA、DB分别为差分结构中两个寄存器的输出,Dout为连接减法器的12位寄存器的最终输出结果。
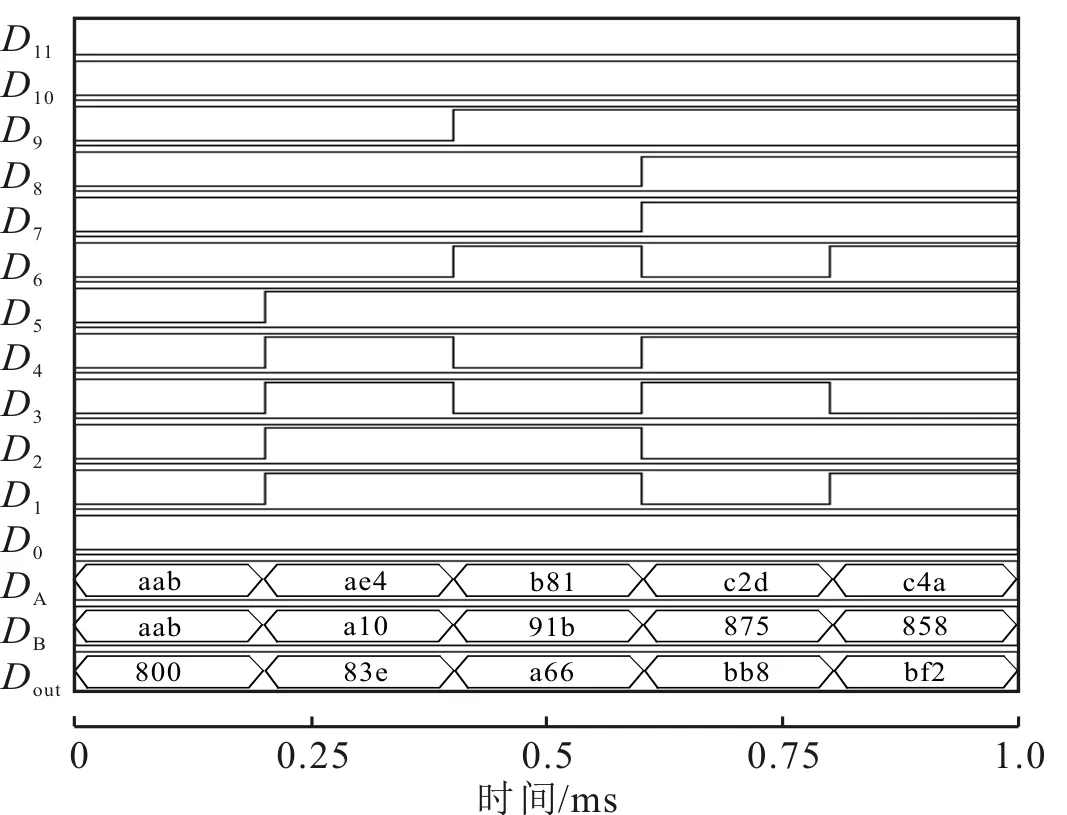
图9 减法器电路的仿真结果
图9中12位减法器运算结果的Dout数据以16进制数的形式表示,为方便计数,需要将Dout转换为十进制表示形式Dout1。另外,由于12位减法器中存在异或门,还需要将Dout1经由异或门实现为Dout2,Dout2由DA、DB的差值加2 048得到,减法器十进制表示及异或门实现结果如表1所示。

表1 减法器十进制表示及异或门实现结果
3.2 VCO-ADC仿真分析
基于180 nm CMOS工艺,设计了12位0.8 V的VCO-ADC。其整体电路由两个通道组成,版图如图10所示。在整体电路版图设计中,两个电容放在最左边的部分,具有对称性的差分输入线Vinn、Vinp在两个电容之间进行走线。为了保证匹配性和对称性,将两个单端VCO-ADC进行对称摆放,为了避免模拟电路与数字电路之间噪声的干扰,将每个模块都用保护环包围。版图总面积为309.26×103.01 μm。

图10 差分VCO-ADC电路版图
使用Verilog HDL硬件描述语言进行校准算法设计,参考文献[7-9],采用了基于查找表LUT的非线性数字校准算法,提取寄生参数完成后仿真,生成校准算法的输入。在Quartus II软件平台上,采用Cyclone IV系列的现场可编程门阵列(Field Programmable Gate Array, FPGA)开发板对校准算法进行硬件验证。
VCO-ADC校准前、后的频谱图分别如图11和图12所示。

图11 校准前VCO-ADC的频谱图
从图11中可以看出,虽然采用差分结构有效抑制了偶次谐波,但受VCO非线性的影响,三次谐波依然明显,经过校准后,VCO的三次谐波有所减弱,如图12所示。
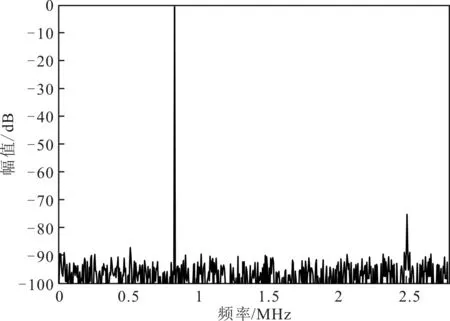
图12 校准后VCO-ADC的频谱图
校准前后VCO-ADC的电路信噪失真比(Signal to Noise and Distortion Ratio, SNDR)和无杂散动态范围(Spurious Free Dynamic Range, SFDR)值随电源电压变化曲线如图13所示。可以看出,随着电源电压的增大,校准前SNDR和SFDR曲线总体呈较明显的上升趋势,而校准后SNDR和SFDR曲线相对平缓,且与校准前相比,校准后SNDR和SFDR提升至70 dB和80 dB左右,提升幅度较明显。
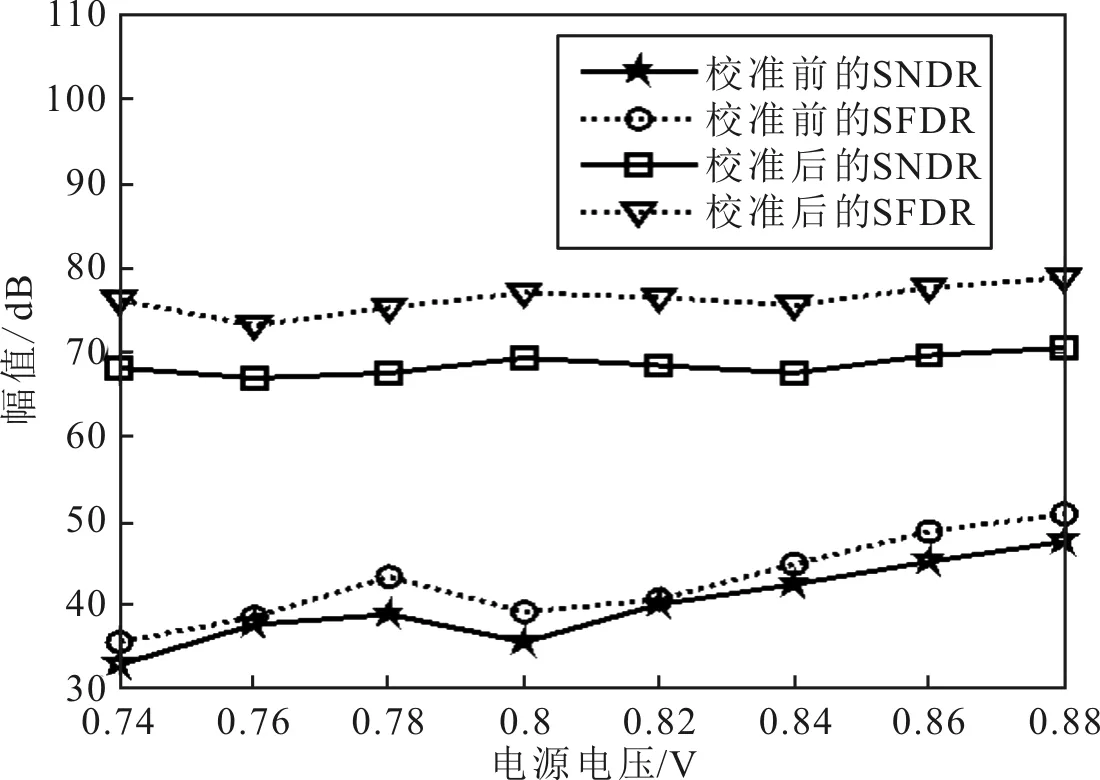
图13 校准前后SNDR和SFDR随电源电压变化曲线
设定电源电压为0.8 V,校准前后VCO-ADC的SNDR和SFDR随输入信号频率变化曲线如图14所示。可以看出,与校准前相比,校准后SNDR和SFDR相对平缓,且校准后SNDR和SFDR分别提升至70 dB和80 dB左右。特别是,在0.8 V电源电压条件下,当输入信号频率为834.96 Hz时,校准前、后电路的SNDR从46.78 dB提升为70.27 dB,SFDR从47.45 dB提升为78.21 dB,提升幅度较明显。

图14 校准前后SNDR和SFDR随输入频率变化曲线
另外,在线性特性方面,校准前、后的微分非线性(Differential nonlinearity, DNL)和积分非线性(Integral nonlinearity, INL)值分别从0.43 LSB和1.15 LSB降低为0.34 LSB和0.65 LSB。在精确度方面,有效位数(Effective Number of Bits, ENOB)从7.48 bit提升至11.38 bit。
所提设计与文献[12]和文献[13]方法的设计性能参数对比如表2所示。可以看出,设计的最大优势是能够在电源电压为0.8 V条件下工作,而其他两种设计工作的电源电压较高。另外,所提设计的电路面积较小、功耗较低,这是因为其他两种数字校准算法均需要模拟电路的支持,会增加电路面积、功耗和电路设计的复杂度。
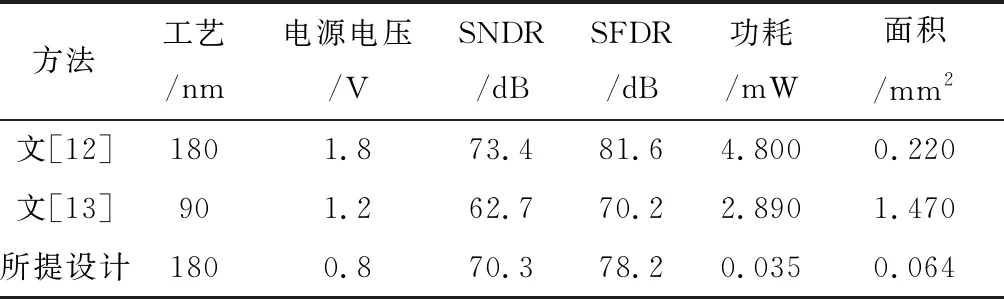
表2 不同设计方法的性能参数对比
4 结语
利用180 nm CMOS工艺设计了一款12 bit的VCO-ADC。ADC采用分裂结构,包含两个VCO-ADC子通道。利用伪随机方式向子通道中加入扰动信号,使用查找表方法对VCO-ADC的输出进行数字后台校准。仿真结果表明,所提设计能够在0.8 V电源电压条件下工作,且ENOB和SFDR较小。另外,设计电路的面积和功耗较低。

