基于POMDP的单用户认知移动边缘计算资源分配
刘伯阳,马 杰,李 伟,万奕尧
(西安邮电大学 通信与信息工程学院,陕西 西安 710121)
受无线终端计算能力普遍较低限制,无线终端难以独立完成第五代移动通信技术(5th Generation Mobile Communication Technology,5G)与超越5G(Beyond 5G,B5G)中出现的很多如增强显示技术(Augmented Reality,AR)、虚拟现实技术(Virtual Reality,VR)等计算复杂度高、时延要求高的业务。另外,在一些物联网场景中,物联网节点有限的计算能力使得其只能对收集的信息做简单的数据发送而不能预处理,从而造成中心节点计算压力过大。
传统的云计算技术允许用户将待计算数据传输至云端,利用云服务器强大的计算能力辅助用户进行计算。然而,用户使用云计算需经过多层网络请求与传输,时延过大,难以满足业务低时延要求。为了解决此问题,移动边缘计算(Mobile Edge Computing,MEC)技术应运而生[1]。MEC将计算服务器下沉至用户边缘,与其建立无线链路,其消耗一定的能量将待计算任务直接卸载至MEC服务器,计算完毕后将计算结果下载至用户,从而可迅速完成计算任务,满足用户业务低时延要求。
目前,几乎所有适合通信的频段都被分配殆尽,频谱资源的稀缺成为广泛部署MEC系统的一个挑战。同时,受体积与成本限制,无线终端难以搭载大容量电池,用户电量与续航能力有限。特别是在物联网场景中,大量物联网节点部署区域不易到达,如何为物联网终端充电也是一个亟待解决的问题。认知无线电(Cognitive Radio,CR)是一种无线频谱共享技术,其允许网络中的未授权用户(Secondary User,SU)对频谱授权用户(Primary User,PU)造成干扰小于一定容限的情况下接入授权用户频段,实现频谱共享,提升频谱利用率[2]。能量收集(Energy Harvesting,EH)技术允许用户从周边环境吸收能量,可提升无线用户续航能力[3]。因此,可将CR、EH与MEC结合,构建CR-EH-MEC系统,为用户提供频谱接入、能量供应与计算服务。
关于EH、CR与MEC的结合已有一些研究。通过在MEC网络中应用EH技术,能够有效提高网络中无线设备续航[4-8]。文献[4]提出一种EH-MEC框架,通过对用户的运行模式、CPU计算频率与卸载功率进行联合优化最小化任务执行时延与任务计算失败代价。文献[5]研究了一种可无线充能的MEC系统并定义了MEC计算概率,即任务被顺利执行的概率,通过对本地计算能耗与任务卸载节能量进行优化,最大化MEC计算概率。文献[6]考虑MEC服务器装备多天线的场景,通过优化发送波束成形矢量、CPU计算频率以及卸载的任务量最小化MEC服务器能耗。文献[7]考虑单天线无线充能MEC协作场景,利用两个用户协作对抗双重远近效应,靠近基站的用户首先帮助远离基站的用户卸载计算数据,然后卸载自身数据。上述工作都是基于频谱资源充足,并可为系统分配专用频段的假设。因此,考虑当前频谱资源的稀缺,上述假设在实际通信系统中难以实现。为了提高系统频谱效率,CR是一项解决频谱稀缺问题的有效技术,得到了广泛的研究[9-12]。文献[9]研究在PU干扰容限约束下系统效益最大化问题。文献[10]提出一种三层CR-MEC网络架构,通过CR技术为网络用户提供频谱接入机会,然而,该研究只提出框架并未开展详细研究。文献[11]与文献[12]对无线充能的CR-MEC系统进行了研究,分别在PU与SU进行协作[11]与不协作[12]场景下,对SU操作参数进行优化最大化其计算能量效率[11]与计算比特数[12]。但是,上述工作没有考虑用户的续航能力。为了提高CR-MEC系统的性能,需要考虑EH技术在CR-MEC系统中的应用,提升系统性能。
MEC与CR-MEC的研究均集中在单个时隙内对MEC服务器与用户参数优化设计,主要集中在MEC系统的瞬时性能上。对无线网络来说,单个时隙的性能最佳不等于长期性能收益最佳,相反,专注于单个时隙的性能可能导致长期性能的下降。为了单个时隙性能最佳,可能会在信道条件很差的情况下投入较大的能量最大化吞吐量。从长远角度考虑,未来时隙中可能会有更好的信道环境,但是可能在之前时隙已耗费过多能量导致无法有效利用更好的信道条件。针对以上问题,拟提出一种基于部分可观测马尔科夫决策模型(Partially Observable Markov Decision Process,POMDP)的单SU多PU CR-MEC网络资源分配方案。考虑单个SU与多个PU共享信道的情景,SU利用POMDP决策每次进行感知与接入的信道,以及接入模式、CPU频率、卸载功率等参数,使得SU长期收益最大。最后,利用计算机仿真结果对所提方案的有效性进行了验证。
1 系统模型
考虑一个由SU、M个PU与一个搭载了MEC服务器的无线接入点(Access Point,AP)构成的认知MEC网络,系统模型如图1所示。所有节点装备单天线且工作在同步时隙结构模式,每个时隙长度为T。假设PU分布在同一较密集区域,SU到每个PU之间的信道增益相同,令eh表示每个时隙SU可吸收的能量。假设信道相干时间是时隙长度的整数倍,即Tc=ΘT,Θ为大于等于1的整数。在信道相干时间Tc内,信道增益保持不变。

图1 系统模型
每个PU在每个时隙均具有两种状态,令sm表示第m个PU的状态,则有sm∈{0,1},0为工作状态,1为空闲状态。与文献[13-16]相同,将每个PU的两个状态建模为一个二状态马尔科夫链,第m个PU状态转移情况如图2所示。
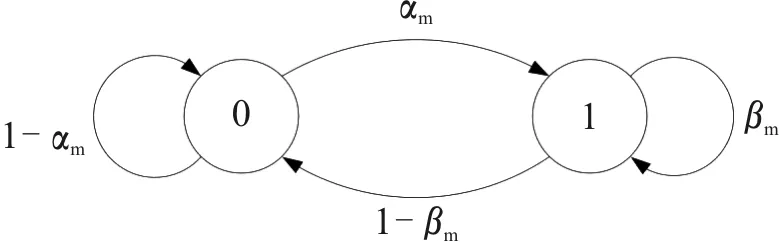
图2 第m个PU状态转移
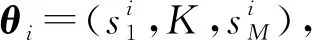
P′=A1⊗A2⊗…⊗AM
其中:Ai为第i个PU的状态转移概率矩阵;⊗为克罗内克积。
令emax表示SU电池最大容量,SU具备EH能力,可从周围环境吸收能量,如太阳能、电磁能等。将EH过程建模为一个伯努利过程,即每个时隙SU以确定概率吸收的能量。伯努利模型可以很好地建模实际环境中能量捕获的随机性与离散性。
令C表示SU计算1 bit数据需要的CPU周期数,f表示SU CPU计算频率,则SU本地计算速率可表示为f/C。若SU向AP卸载计算任务,当PU处于空闲状态时,SU可卸载成功,AP成功接收后向SU返回确认信息字符(Acknowledge Character,ACK),即ACK为1。若PU处于占用状态,SU卸载数据与PU传输发生碰撞,不返回ACK,即ACK不为1。

其中,RSN为PU信号接收信噪比。
其中,t为积分变量。
2 问题建模
SU对PU的状态检测存在误差,即其不可能完全获知PU的状态,需根据观察值对PU所处的真实状态进行推测。而PUs联合状态转移具有马尔可夫性,因此,采用POMDP对SU进行策略决策。
在POMDP模型中,每个时隙开始时SU对PUs的联合状态具有一个推断,即信念概率,记为Bt=[bt(θ1),…,bt(θN)],其中,bt(θi)表示SU认为在时隙t下PUs处于状态θi的概率。
POMDP包含状态、状态转移概率、行为、奖励、观察值、观察概率以及策略等7个要素。对应于相应场景,环境为PUs,决策者为SU,系统状态为(es,t,Bt),其中,es,t为时隙t开始时SU的可用能量。在POMDP决策中SU在时隙t的行为表示为At=(mt,ea,t,ζt),其中:mt为SU在时隙t选择的感知与接入PU信道,即SU在时隙t时对第mt个PU信道进行频谱感知;ea,t为SU在时隙t拟投入执行MEC的能量;ζt为SU操作模式因子,ζ=1,则SU只进行本地计算,ζt=2,则SU采用部分卸载模式,将一部分任务在本地计算,另一部分任务卸载至AP进行远程计算。POMDP在时隙t的奖励对应SU在该时隙能完成的计算任务量(Calculated Number of Bits,CNoB)。
在SU做出决策后,其能获得的奖励和CPU工作频率与SU卸载功率p有关,当At=(mt,ea,t,ζt=1)时,SU能获得的最大奖励为
其中,
η为SU每个CPU周期耗能功率系数。当At=(mt,ea,t,ζt=2)时,SU能获得的最大奖励为优化问题P1,其最优目标函数值表示为
s.t.C1:p(T-τ)+ηf(T-τ)≤ea,t
C2:0≤f≤fmax
C3:0≤p≤pmax
其中:W为第mt个PU信道带宽;pmax为SU最大卸载功率;g表示SU与AP之间的信道功率增益;C1为能量因果限制;C2与C3分别为SU的CPU计算频率与发送功率限制。所建优化问题为凸问题,可用Karush-Kuhn-Tucker Conditions条件[18]对其求解。当ea,t≤pmax(T-τ)+ηfmax(T-τ)时,利用KKT条件,最优解为
其中,
其中,σ2表示噪声功率。

在每个时隙进行决策并执行决策后,SU将观察到一个观察值O,根据此观察值对SU认为在时隙t下PUs处于状态θi的概率进行更新,其表达式为

SU能获得的真实奖励还与PU真实状态有关,PU真实状态可通过观察值进行推断。SU执行行为At后可能观察到6种观察值,下面分别对这6种观察值以及对应的观察概率进行分析。
当采取行为为At=(mt,ea,t,ζ=1)或ea,t=0时,对6种观察值进行逐一分析。







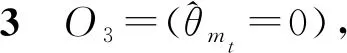


其中,Ix为指示函数,如果x为真,则Ix=1,否则,Ix=0。



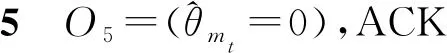





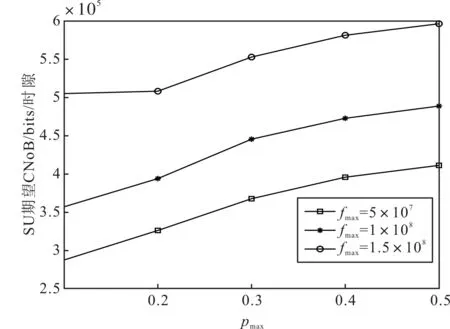
当SU行为为At=(mt,ea,t,ζt=2),且0 SU执行行为At后,其可用能量转移概率为 频谱感知只是对信号进行接收判决,其耗能相比MEC耗能小的多,可以忽略不计。 通过POMDP对SU行为进行决策,找到最优策略,即SU在特定状态下进行选择何种行为的方案,使得SU在相干时间内得到期望奖励之和最大。通过Bellman方程对最优策略进行求解,针对所提系统模型,可建立Bellman方程为 (1) 表1 仿真参数 图3展示了PU用户数为2时SU期望CNoB即平均每个时隙的CNoB与γ、时间步长Θ的关系曲线。由图3可观察到当γ较小时SU期望CNoB随着时间步长增加而减小。当γ较大时,CNoB随着Θ增大而增大。γ反应了SU对在当前行为下未来能获得CNoB的重视程度。γ越大,SU越看重未来收益,越小则越看重短期效益。当γ较小时,SU主要考虑短期时隙收益,时间步长越长则平均收益越小。反之当γ越大时,SU优化对未来长期收益更有利,因此,期望CNoB随着γ增加而增加。 图3 SU期望CNoB与γ、Θ的关系曲线(M=2) 图4展示了SU期望CNoB与其最大CPU计算频率fmax、最大发送功率pmax的关系,其中PU用户数为2。fmax与pmax的增大,SU的决策空间变大,因此,收益必然增大。图4也可间接证明所提算法的正确性。 图4 SU期望CNoB与fmax、pmax的关系曲线(M=2) 图5和图6展示了在PU用户数为2的情况下,SU期望CNoB与检测概率pd以及感知时间长度τ的关系曲线。 图5 SU期望CNoB与pd、τ的关系曲线(M=2) 图6 SU期望CNoB与τ的关系曲线(M=2) 从图5可以看出,在感知时间长度τ不变的情况下,检测概率增加将导致虚警概率的增加,因此,随着检测概率增加SU期望CNoB下降。SU易将PU空闲检测为PU工作,错失频谱接入机会。从图5还可看出,SU收益与τ也有关系。图6对SU收益与τ的关系进行了仿真,可以看出,τ增加将有效减小虚警概率,提升空闲频谱挖掘能力,因此,随着τ的增加,SU收益先增大后减小。但是,也会导致SU进行MEC的时间变短,使收益降低。因此,出现图6中所示的现象。 图7展示了SU期望CNoB与PU用户M、EH概率ρ的关系曲线。由图7可以看出,SU期望CNoB随着M与ρ的增加而增加。PU用户增加SU将有更多的频谱接入选择,具有更多的频谱接入机会。能力捕获概率增加则SU将有更稳定的续航能力,因此,此二者的增加都将使得SU期望CNoB增加。 图7 SU期望CNoB与PU,M、ρ的关系曲线 针对当前认知边缘计算只考虑当前单个时隙性能最佳而未考虑长久期望性能最佳的问题,研究一种由一个次用户、多个主用户与一个无线接入点构成的认知边缘计算网络。在一个次用户、多个主用户网络中利用POMDP对次用户计算损耗、操作模式、CPU计算频率与卸载功率进行优化。仿真结果表明,就长期期望计算数据量而言,所提的方案显著优于单时隙优化方案,能够有效地提升频谱效率,缓解移动边缘计算网络中的频谱稀缺问题。





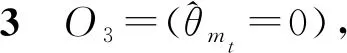





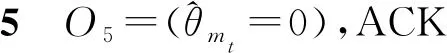






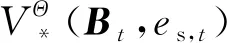
3 性能仿真及分析




4 结语

