激波风洞高低压段钢膜片破裂特性研究1)

聂少军 汪运鹏,2) 薛晓鹏 姜宗林

*(中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)

†(中国科学院大学工程科学学院,北京 100049)

**(中南大学航空航天学院,长沙 410083)

引言

激波管是实验室中能够产生可控激波并且利用激波压缩试验气体的常用试验装置,用来模拟实际工作条件,它能瞬间将试验气体升温、加速和增压[1].激波风洞由一个激波管以及连于其后的喷管、实验段等风洞主要部件组成,包含相连的驱动段和被驱动段,驱动段贮存高压、高能量的工作气体,被驱动段贮存低压试验气体,试验前两者通常被膜片隔开.试验时,上游的驱动段气体经过爆轰驱动[2]或者其他驱动方法[3-4]产生脉冲高压,巨大的压差会导致膜片破裂,继而在下游产生所需的运动激波.在进行激波风洞试验时,膜片不仅需要承受驱动段的初始充气压力并且不发生破裂,而且还需要保证在点火驱动时完全打开而且不发生脱落.膜片能够瞬间打开并且完全打开是形成激波的关键前提条件,同时也是激波风洞试验中普遍存在的难题.

国外一些激波管专家学者针对膜片破裂特性进行了相关研究.在20 世纪50 年代,一些学者通过激波管试验对膜片破裂的规律进行研究,发现膜片破裂打开是一个非瞬态过程[5-6].随后,有学者从理论上建立了简单的膜片破裂的理论模型,通过实验研究了有效破膜时间与膜片材料的关系,但是理论模型与实验获得的破膜时间存在较大差距[7].随后,Hickman 等[8]通过实验研究的方法获得了膜片开启过程中的高速阴影照片,观测到了膜片开启时存在的拟定常自由射流.范良藻和俞鸿儒[9]进一步研究了膜片材料对有效破膜时间的影响,结果表明有效破膜时间与激波管直径和膜片材料密度成正相关关系,与膜片压差成负相关关系.林建民[10]研究了激波风洞中不同外形膜片对破膜压力的影响,比较了金属成型膜片和平板膜片的承载能力,发现金属成型膜片更适合用于爆轰驱动的激波风洞.栗继伟[11]研究了不同膜片厚度对破膜过程造成的压力损失的影响,在JFX 氢氧爆轰驱动激波风洞中进行试验,结果表明膜片总厚度和有效厚度对破膜压力损失影响较大,当厚度增大时,破膜压力损失也会相应增大.

随着计算机技术的发展,学者已不再局限于实验研究方法,针对激波管中膜片破裂过程的数值模拟方法成为可能.目前已有学者通过数值方法模拟了卡鲁尼亚大学的SS304 激波管中的膜片破裂过程,分析了在不同厚度(1 mm,2 mm 或3 mm)的情况下铝膜片的破裂过程,包括破膜压力和膜片开启时间随膜片厚度的变化规律,得到的结论为:当膜片的无量纲厚度(即膜片有效厚度与膜片总厚度的比值)分别为0.33 和0.67 时,有效厚度越小,膜片破裂所需的压力越小,破裂所需的时间越长[12].

为了研究风洞中膜片的破裂特性规律,一些学者主要采用传统风洞试验的方法研究了铝膜片的厚度对破膜压力和有效破膜时间的影响,而对钢膜片的研究比较少,因为传统风洞试验中铝膜片的承压能力已能达到试验要求.在目前的激波风洞试验中,鲜有学者采用数值模拟的方法研究脉冲型风洞中膜片的破裂过程,尤其是膜片的凹槽长度对破裂过程的影响.

因此,本文将采用数值模拟的方法,利用有限元分析软件中的显式动力学模块对膜片破裂过程进行瞬态结构分析,并与复现高超声速飞行条件激波风洞(以下简称“JF-12 复现风洞”)[13]中的试验结果进行比对,分析爆轰驱动的激波风洞中不同有效厚度、总厚度和凹槽长度对膜片破裂特性的影响.从工程应用的角度来看,探寻激波风洞中高低压段膜片的破裂特性有助于预测膜片在风洞运行中打开时的压差与破膜时间,节省试验成本,缩短试验时间,提升试验流场品质,促进我国激波风洞试验研究的有利发展.本工作采用有限元数值模拟的方法,推导了膜片破裂的动力学方程,研究了膜片破裂特性规律,以期为JF-12 复现风洞试验提供参考数据.

1 膜片破裂的动态模型建立及研究方法

2012 年中国科学院力学研究所成功研制了JF-12 复现风洞,该风洞可复现25～40 km 高空、马赫数5～9 的飞行条件的飞行器气动试验,有效试验时间超过了100 ms[14-17].该风洞由卸爆段、爆轰驱动段、激波管段、喷管、试验段和真空段等部分组成.卸爆段和爆轰驱动段、爆轰驱动段和激波管段、激波管段和喷管段均有膜片隔开,爆轰驱动段和激波管段管道为等截面圆柱形,主膜片是指爆轰驱动段和激波管段之间的膜片[18-19].常见的爆轰驱动技术有正向爆轰和反向爆轰两种运行模式[20],JF-12 复现风洞采用反向爆轰驱动技术[21-22]产生高温高压气体.本文在数值模拟的过程中,采用阶跃载荷压力模拟试验中爆轰驱动产生的压力.在爆轰驱动的激波风洞试验中,爆轰驱动段和激波管段管道的刚度远大于膜片的刚度,理论分析时可将管道视作固定端.研究方法是通过有限元软件对膜片的破裂过程进行动态模拟,将模拟结果与JF-12 复现风洞试验结果进行对比分析.研究目标是通过数值模拟方法对激波风洞中膜片破裂的特性规律进行研究,为JF-12 复现风洞试验提供膜片参考数据.

1.1 膜片几何模型

激波风洞中的主膜片如图1 所示,膜片可以简化为一个圆柱体,圆柱体的高即膜片的总厚度,在膜片的中心开有适当深度的互相交叉垂直的“十”字形凹槽,凹槽的作用是使膜片顺着凹槽顺利打开,保证膜片打开的质量.采用三维建模软件绘制膜片模型,如图2 所示.

图1 激波风洞主膜片示意图Fig.1 Schematic diagram of main diaphragm of shock tunnel

图2 主膜片模型Fig.2 Main diaphragm model

膜片有效厚度E是膜片总厚度T与膜片凹槽深度D之差,膜片的凹槽长度是基于爆轰驱动段和激波管段管道内径设定的.膜片模型尺寸信息见表1.

表1 膜片模型尺寸信息(单位:mm)Table 1 Main diaphragm model size information(Unit:mm)

在上述模型的基础上,利用三维建模软件建立了不同总厚度T、有效厚度E和凹槽长度L的膜片模型,总厚度有3.5 mm,2.5 mm 和1.5 mm 三种类型,有效厚度有0.5 mm,1 mm 和1.5 mm 三种类型,凹槽长度设定有400 mm,380 mm 和360 mm 三种类型,具体尺寸如表2 所示.

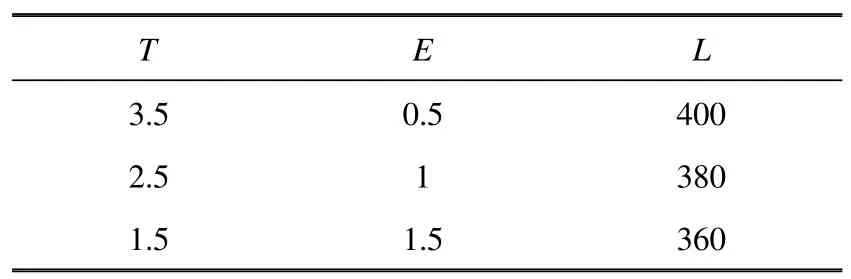
表2 不同外形的膜片模型尺寸信息(单位:mm)Table 2 Dimensional information of diaphragm models with different shapes(Unit:mm)

1.2 膜片破裂的动力学模型

针对激波风洞试验,在爆轰压力的作用下,膜片破裂是一个典型的非线性动力学问题,膜片破裂时膜片周围复杂的流动模式以及膜片内部的动态应力-应变过程导致该问题十分复杂,如图3 所示.为了简化该问题,便于研究,假设膜片在没有任何变形的情况下瞬间破裂;膜片的作用力均匀分布且是开口面积的线性函数;在破裂过程中,膜片弯曲应力产生的力矩为常数[8].

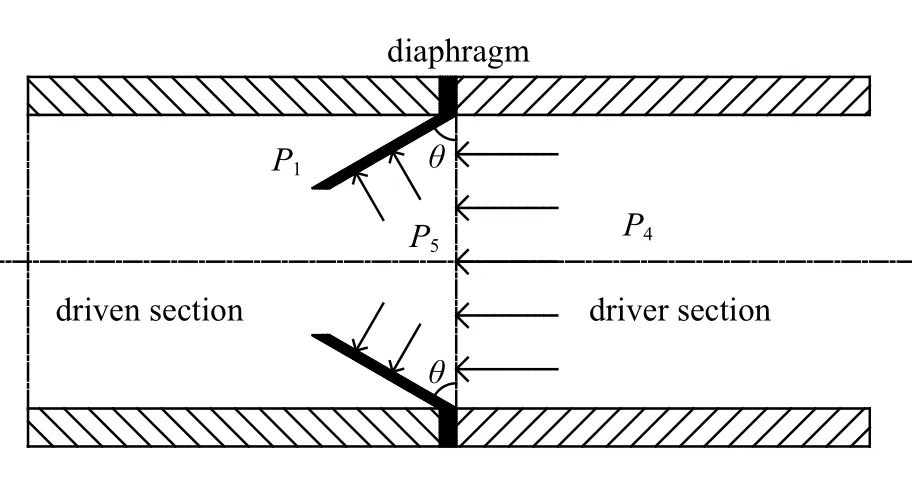
图3 膜片打开过程示意图Fig.3 Schematic diagram of diaphragm opening process

根据刚体定轴转动微分方程,膜片打开角度θ满足

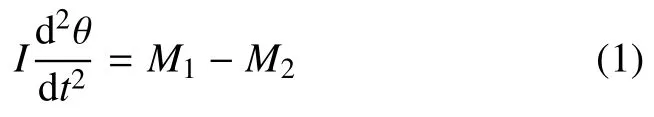
式中,I是膜片绕轴的转动惯量,M1和M2分别是高低压力差和膜片弯曲应力产生的力矩,表达式为

式中,P5和P1分别为作用在膜片上游和下游的压力;A为膜片有效面积;为膜片内径的长度;P4为驱动段的初始压力;S是无量纲强度参数,表示膜片弯曲应力力矩与膜片最大力矩的比值,根据假设,在膜片破裂过程中,S为常数.

为了便于分析膜片打开角度θ,令

将式(5)积分一次,得

将式(6)积分一次,即可得到

由式(7)可知,当τ=0 时,θ=0°,dθ/dτ=0,膜片处于初始状态,未发生破裂;当θ=90°时,膜片完全打开完成破裂.

1.3 研究方法

在完成模型建立之后,采用有限元分析软件中的显式动力学对膜片破裂过程进行数值模拟计算.显式动力学是一种基于显式算法对动力学方程进行求解的方法,具有较好的稳定性,一般不存在收敛性问题[23].显式动力学适合用于解决短时间(ms)内发生的事件,如瞬态、大应变、大变形、材料的破坏、材料的完全失效或者伴随复杂接触的结构问题.采用显式动力学模块对膜片进行有限元分析的步骤如下图4 所示.

图4 膜片破裂过程数值计算流程图Fig.4 Flow chart of numerical calculation for diaphragm rupture process

膜片破裂过程的数值模拟计算步骤包括计算前处理、计算和计算后处理操作,计算前处理操作主要包括建立膜片几何模型、设置膜片材料性质、划分膜片网格以及建立膜片初始边界条件;计算后处理是对计算结果进行相关操作,以输出变形、应变、应力等结果,具体包括查看结果、输出结果、误差估计等内容.

1.3.1 膜片材料性质

膜片材料是影响膜片破裂的重要因素之一,选择膜片材料时,应保证破膜压力的稳定,即破膜过程中保证破膜压力不变;同时,膜片应当具有一定的承压能力,在初始高压作用下,膜片不能被剪切破坏,而在阶跃载荷作用下,膜片需要顺利打开且不发生脱落.传统风洞试验中,高压区和低压区的压差不大,膜片材料可以选择纯铝,但是在激波风洞试验中,爆轰压力可以达到十几兆帕甚至几十兆帕,因此常采用钢(STEEL 4340)膜片,其具体参数如表3 所示.

表3 STEEL 4340 材料属性Table 3 STEEL 4340 material properties

1.3.2 膜片网格划分

在有限元分析计算中,只对网格单元和节点进行计算,在计算之前需要对膜片模型划分网格.增大网格密度可以适当提升计算精度,但是不能弥补错误的假设和输入带来的错误,同时,网格密度过大会导致计算量和CPU 计算时间剧烈延长,而且随着网格的加密,计算机浮点运算的舍入误差也会变大.理想的网格密度应该首先满足计算精度的要求,其次,当网格细化到一定程度后,计算结果的变化可以忽略不计,此时便得到理想的网格密度[24].在经过多次尝试之后,确定了膜片深度为2.5 mm 时网格划分的一些参数设置,如图5 所示.

图5 膜片网格Fig.5 Diaphragm mesh

网格总体单元尺寸为3 mm,凹槽面处网格单元尺寸为2.5 mm,网格节点数为59 885,网格单元数为206 433.

1.3.3 初始边界条件设定

在完成网格划分之后,接下来是设定膜片破裂过程的初始边界条件,具体包括计算时间设定、膜片的载荷设置和固定约束设置.

有限元计算时间的设定需要考虑两个方面的因素:一是必须保证膜片能够在计算时间内完全打开;二是计算时间必须满足实际情况,不应超过激波风洞试验的总时长,综合考虑将数值计算时间设置为1000 μs.

考虑实际情况,膜片受力简化为压力载荷作用,如图6 和图7 所示.在初始充气压力作用下,即0～200 μs 内,膜片正面受力为2 MPa,背面受力为38 kPa,方向垂直于膜片平面;在t=200 μs 时,产生爆轰压力,膜片正面压力骤增至32 MPa,背面压力不变,即在200～1000 μs 内,膜片正面压力为32 MPa,背面压力为38 kPa,压力载荷具体计算过程将在第2章中给出.

图6 高压区压力Fig.6 High pressure zone pressure

图7 低压区压力Fig.7 Low pressure zone pressure

激波风洞管道的刚度远大于膜片的刚度,在试验时膜片被夹膜机夹在管道中,故将膜片外环的圆环面和侧面设置为固定约束,如图8 所示.

图8 固定约束设置Fig.8 Fixed constraint settings

2 计算结果与验证分析

2.1 JF-12 复现风洞试验

膜片破裂的计算前处理操作非常重要,其决定了计算过程的质量好坏,从而直接决定了计算结果的准确性.为了验证计算方法的可行性,在JF-12 复现风洞中进行了激波风洞试验.

根据Chapman 和Jouguet 提出的CJ 模型[25],爆轰波可以视为一个带有化学反应的并且不断释放能量的激波.可燃气体高速传播的爆轰波是带有放热化学反应的强间断面的传播过程,且化学反应瞬时完成,Rayleigh 线和Hugoniot 曲线的切点代表着自持爆轰的稳定终态,即CJ 条件[26-29].

在点火起爆后,驱动段的压力剧烈增大,考虑到实际情况,为了简化膜片破裂的问题,此时假设驱动段的压力瞬间达到CJ 爆轰的压力状态,即作用在主膜片正面的压力突变为CJ 压力,在该压力条件作用下,膜片瞬间被打开.后续工作将考虑采用非定常爆轰压力条件进行更为深入的破膜特性研究.

2.2 计算结果验证

本节模拟的是爆轰驱动段与激波管段中的主膜片破裂情况,膜片外径为540 mm,内径为400 mm,总厚度为3.5 mm,有效厚度为2.3 mm,中心部分开有“十”字形凹槽,凹槽长度为400 mm,宽度为3 mm.在JF-12 复现风洞中进行试验时,高压段爆轰初始压力为2 MPa,低压段充气压力为38 kPa,根据CJ 爆轰理论,爆轰驱动后的高压区压力为32 MPa,低压区压力为38 kPa 保持不变,试验结果和数值计算结果分别如图9 所示.

图9 膜片计算结果验证(左图为JF-12 复现风洞试验结果,右图为数值计算结果)Fig.9 Verification of diaphragm calculation results(The left is the wind tunnel test results reproduced by JF-12,and the right is the numerical calculation result)

将数值模拟计算的结果与JF-12 复现风洞中试验中的膜片结果进行定性比较,可以看出膜片的破裂程度基本一致,说明了数值计算结果比较准确,保证了计算结果的可靠性.因此,可以用数值计算结果模拟激波管试验的结果,且模拟效果比较理想.

3 膜片破裂过程数值分析

本节针对不同总厚度、有效厚度和凹槽长度的钢膜片,保持膜片宽度为3 mm 不变,通过数值模拟方法研究了对膜片破膜压力和有效破膜时间的影响.破膜压力ΔP指膜片破裂时高、低压区的压力差,有效破膜时间τ0为膜片从开始破裂到完全打开的时间差,总破膜时间t为施加压力起至完全打开的时间差.

图10 是钢膜片计算过程示意图,膜片总厚度为3.5 mm,有效厚度为2.3 mm,凹槽长度为400 mm.膜片在第544.45 μs 时发生破裂,在第1100.00 μs 时完成破裂,破裂过程持续了555.55 μs.膜片首先在凹槽中心处发生破裂,产生一个小开口,在相同作用力下,凹槽中心处的结构最易破裂.随着时间推移,开口顺着凹槽扩展,膜片凹槽逐渐破裂,最后带动整个膜片呈现花瓣状的向外撕裂.膜片破裂过程持续了一段时间,而非瞬态破裂,这与实际情况相符,有效破膜时间大约是总破膜时间的一半,比较接近文献[30] 提供的结果.

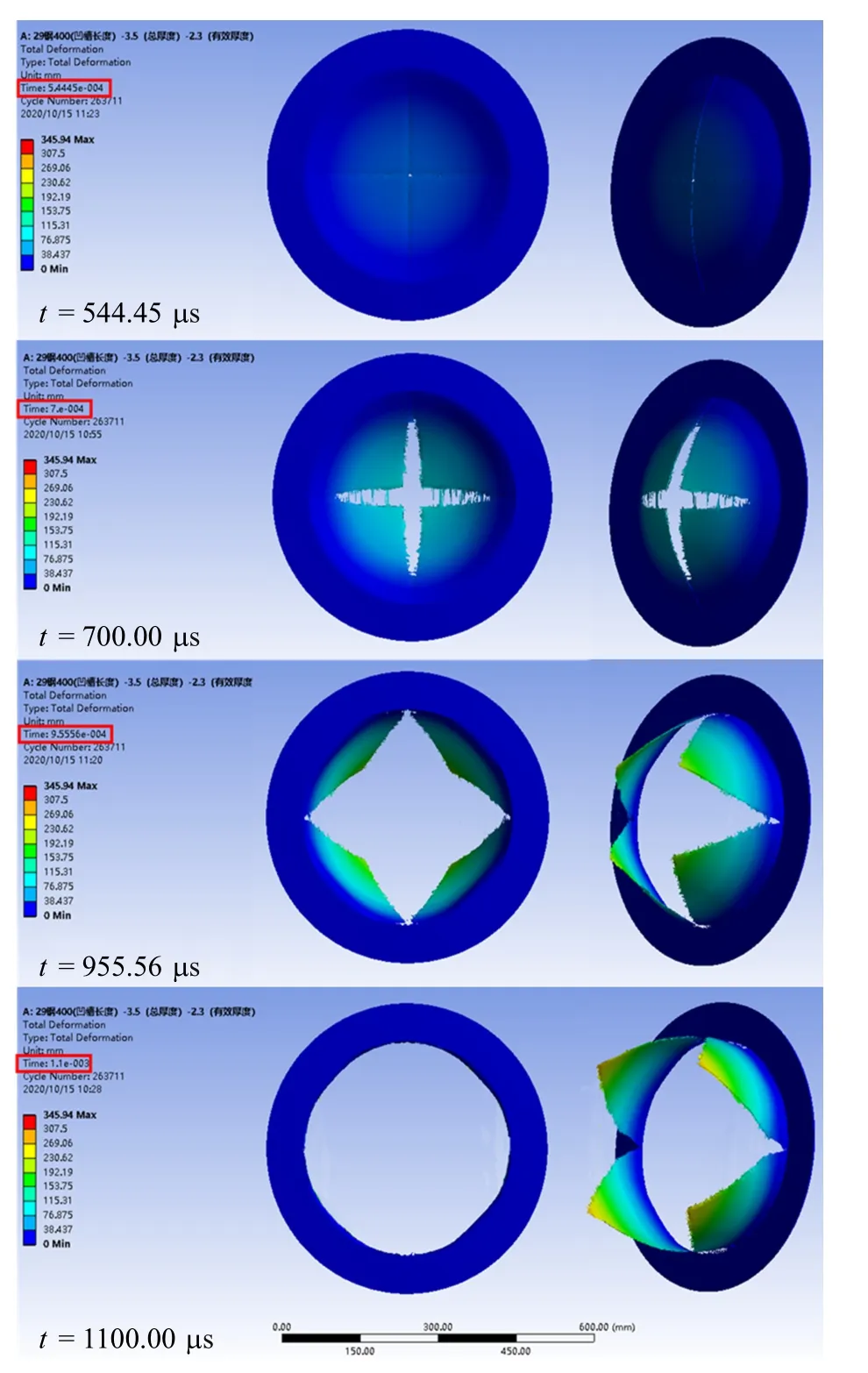
图10 膜片计算结果示意图Fig.10 Schematic diagram of diaphragm calculation results

3.1 膜片有效厚度对破膜影响

膜片有效厚度E通过改变膜片凹槽处的深度来影响膜片的破裂特性,在试验时,应当设置合适的膜片有效厚度保证试验的可行性.表4 展示了钢膜片在不同膜片有效厚度时的计算结果,膜片总厚度为3.5 mm,膜片凹槽长度为360 mm.为了便于观察分析,将表4 中的计算结果绘制成坐标曲线图,横坐标为膜片有效厚度,纵坐标分别为有效破膜压力和有效破膜时间,如图11 和图12 所示.

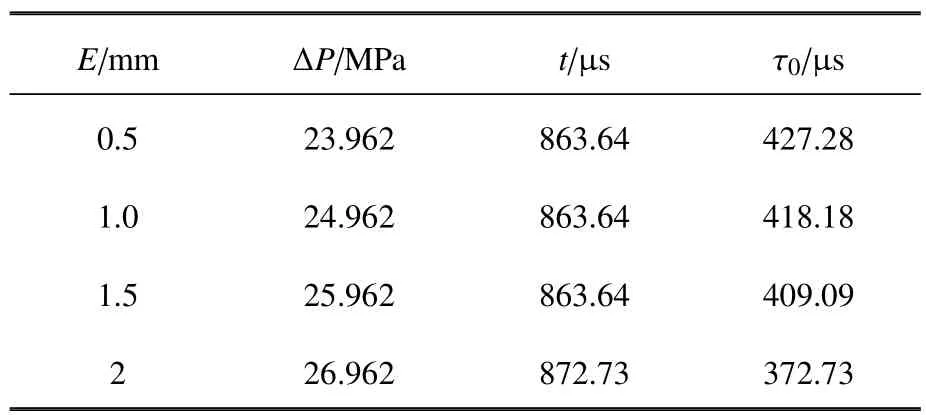
表4 不同膜片有效厚度计算结果Table 4 Calculation results of effective thickness of different diaphragm

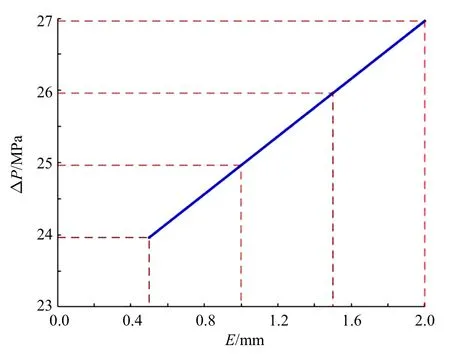
图11 膜片有效厚度对破膜压力的影响Fig.11 Effect of effective thickness of diaphragm on diaphragm rupture pressure

图12 膜片有效厚度对有效破膜时间的影响Fig.12 Effect of effective thickness of diaphragm on effective diaphragm rupture time

图11 和图12 展示了钢膜片在膜片总厚度和凹槽长度一定时,其破裂情况随膜片有效厚度的变化情况.随着膜片有效厚度的增大,膜片的有效破膜压力增加,有效破膜时间减少.其原因是当膜片有效厚度增加时,即膜片凹槽深度减小,此时需要更大的破膜压力将膜片凹槽处的材料击破,随后再带动整个膜片破裂.当膜片凹槽中心破裂时,随着破膜压力的增加,此时会加快整个膜片破裂的过程,膜片持续打开的时间减少,即膜片的有效破膜时间会随着膜片有效厚度的增大而缩短.

3.2 膜片总厚度对破膜影响

在膜片凹槽打开后,膜片的总厚度T通过改变瓣膜的厚度来影响破膜压力,膜片的总厚度对激波管试验也会产生比较大的影响.试验中,膜片的总厚度过大会导致膜片在短时间内不易破裂,而过薄的膜片无法承受巨大的爆轰脉冲压力,容易脱落对流场产生不利的影响.因此,膜片的总厚度选择十分重要,应该选择合适的膜片厚度进行试验.考虑实际情况,在计算过程中,保持膜片无量纲厚度E/T(即膜片有效厚度与膜片总厚度的比值)不变,改变膜片总厚度进行研究.表5 展示了无量纲厚度为0.43 和0.57时钢膜片的计算结果,膜片凹槽长度为400 mm.同样,将表5 中的计算结果绘制成坐标曲线图,如图13和图14 所示.

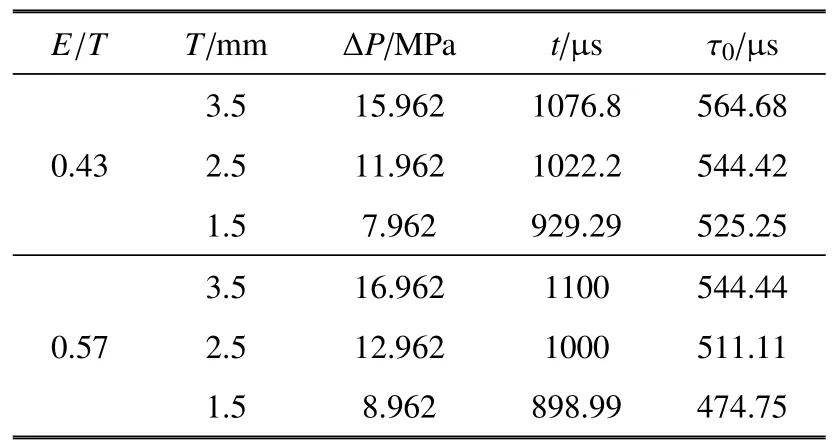
表5 不同膜片总厚度计算结果Table 5 Calculation results of different diaphragm total thickness

图13 和图14 展示的是当无量纲厚度为0.43 和0.57 时,膜片总厚度对破膜压力和有效破膜时间的影响.发现有效破膜时间与膜片总厚度呈现正相关线性关系,当膜片总厚度越大时,其膜片有效厚度也越大,需要更大的破膜压力将膜片凹槽处的材料击破,同时需要更大的破膜压力将膜片瓣膜完全打开,因此,破膜压力随着膜片总厚度的增大而增大.由于膜片总厚度和膜片有效厚度的增大,整个膜片的打开过程变得缓慢,所以膜片有效时间随着膜片总厚度呈现正相关线性关系.

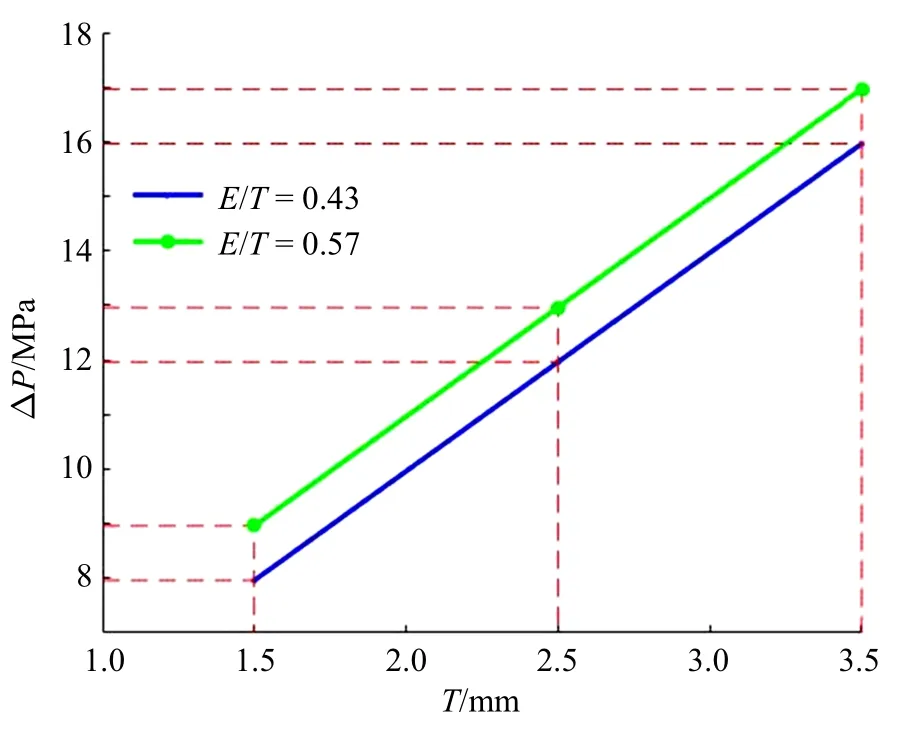
图13 膜片总厚度对破膜压力的影响Fig.13 Effect of total thickness of diaphragm on diaphragm rupture pressure

图14 膜片总厚度对有效破膜时间的影响Fig.14 Effect of total thickness of diaphragm on effective diaphragm rupture time

在图13 和图14 中,曲线变化趋势一致,当膜片总厚度一定时,无量纲厚度变大,此时的膜片破膜压力会增加,而有效破膜时间会减小.造成这一现象的原因与膜片有效厚度影响规律一致,即膜片有效厚度的增大会导致破膜压力的增大和有效破膜时间的缩短.

3.3 膜片凹槽长度对破膜影响

在目前关于激波管膜片的研究中,尚未有关于膜片凹槽长度对膜片破裂的影响规律.凹槽长度L通过改变膜片凹槽的打开时间来影响膜片的破膜压力和有效破膜时间.表6 展示了钢膜片凹槽长度对膜片破裂特性的影响,膜片总厚度为3.5 mm,无量纲厚度分别为0.43 和0.57.将表6 中的计算结果进行处理,绘制成坐标曲线图,如图15 和图16 所示.

图15 膜片凹槽长度对破膜压力的影响Fig.15 Effect of diaphragm groove length on diaphragm rupture pressure

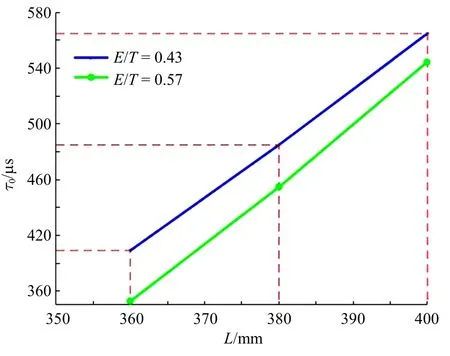
图16 膜片凹槽长度对有效破膜时间的影响Fig.16 Effect of diaphragm groove length on effective diaphragm rupture time

在图15 和图16 中,当膜片总厚度和无量纲厚度一定时,膜片的破膜压力与膜片凹槽长度呈现负相关线性关系,膜片有效破膜时间与凹槽长度呈现正相关线性关系.膜片凹槽长度增大时,增大的凹槽处有效厚度减小,相应所需要的破膜压力也减小,所以破膜压力会相应减小.但是膜片的总厚度保持不变,破膜压力的减小会减缓膜片瓣膜打开的过程,所以相对应的有效破膜时间增加.

3.4 膜片尺寸优化问题

在激波风洞中进行试验时,当膜片选择确定后,根据膜片破裂的特性规律可以有效预测膜片的破膜压力和有效破膜时间.同时,当激波风洞中的破膜压力一定时,研究激波管中的膜片破裂特性有助于风洞试验中膜片的选取.在激波风洞中,我们希望膜片在破裂时能够顺利打开,而且打开的过程越快越好,理想情况下我们认为膜片瞬间完全打开,因此膜片总破膜时间越短越好.同时,膜片破裂的过程中不能出现脱落的情况,保持破膜压力不变,不能影响激波风洞气流品质.针对JF-12 复现风洞,根据膜片破裂的特性提出了一种设计方案,适合采用钢作为膜片材料,如表7 所示.

表7 JF-12 复现风洞膜片优化方案Table 7 Diaphragm optimization scheme of JF-12 reproduction wind tunnel

膜片外形因素在一定程度上影响膜片的破裂情况,针对具体风洞试验,需要根据实际情况判断破膜压力的大小.在破膜压力较大时,需要选取相应较厚而且凹槽长度较小的膜片.一般总破膜时间较短,因此常选用总厚度适中,有效厚度较小,凹槽长度较小的钢膜片进行激波管试验.

4 结论

在激波风洞试验前,膜片将激波管分为两段,将高低压气体隔开,创造相互独立的气体环境.在试验时,膜片在脉冲压力的作用下破裂完全打开,在被驱动段产生运动激波,创造所需的来流条件.传统的实验研究鲜有学者研究爆轰驱动的激波风洞中膜片的破裂特性.本文采用有限元分析软件模拟计算了膜片破裂过程,计算结果与试验结果吻合得比较理想.基于有限元数值模拟技术研究了膜片外形参数(膜片有效厚度、总厚度和凹槽长度) 对于膜片破裂过程的影响,并给出了一种激波管用膜片的优化设计方案.

根据数值计算结果,膜片首先从凹槽中心处开始破裂,然后开口顺着凹槽破裂,随后带动整个膜片瓣膜破裂.在钢膜片总厚度一定时,破膜压力与膜片有效厚度呈现正相关线性关系,有效破膜时间与膜片有效厚度近似呈现负相关线性关系.在钢膜片无量纲厚度一定时,破膜压力和有效破膜时间均与膜片总厚度呈现正相关线性关系.破膜压力与膜片凹槽长度成负相关线性关系,有效破膜时间与膜片凹槽长度成正相关线性关系.

研究激波风洞中主膜片的破裂特性将有助于预测破膜压力和有效破膜时间,便于激波风洞中参数设置,为激波风洞试验提供计算依据,具有现实意义和工程实践意义.