加工中心三轴联动精度测量方法研究
赵宏安 吴慧敏
(通用技术集团大连机床有限责任公司,辽宁 大连116620)
在通用加工中心圆度精度测试中,常利用球杆仪通过评价两个正交的移动轴联动圆周运动误差实现,根据测得的误差圆周运动轨迹分析出比例不匹配、反向间隙、反向越冲及垂直度等精度指标来进行机械结构的调整和优化。
通常情况下,对于三轴加工中心的圆度精度测量方式是只能通过球杆仪两轴联动测量实现,3个平面分别测量,然后再对机床进行调整或优化,所以测量效率不高,三轴联动精度不能获得。本文针对三轴加工中心精度测量,结合球杆仪结构与测量特性,提出了以四叶螺旋线为测量运动轨迹的三轴联动测量方法,可有效分析三轴加工中心垂直度、比例不匹配、反向间隙及反向越冲等多项精度指标,有利于提高三轴加工中心精度测量效率。
1 球杆仪测量模型
1.1 球杆仪结构原理
球杆仪由2个精密球头和1个高精度伸缩线性传感器构成。测量时,两球头通过磁性球座分别安装于相对运动的两构件(通常是工作台和主轴)上,运动过程中记录两球头间相对距离变化,并依据此变化情况分析机床各项运动精度指标。受限于球杆仪本身结构特点,两球头间相对运动轨迹需为球面轨迹,如常用的圆轨迹即为空间球面轨迹的特例。
1.2 三轴测量的运动求解模型
采用球杆仪测量三轴加工中心时,球杆仪两球头SA和SB分别安装在可升降主轴端与两自由度工作台上,如图1所示。
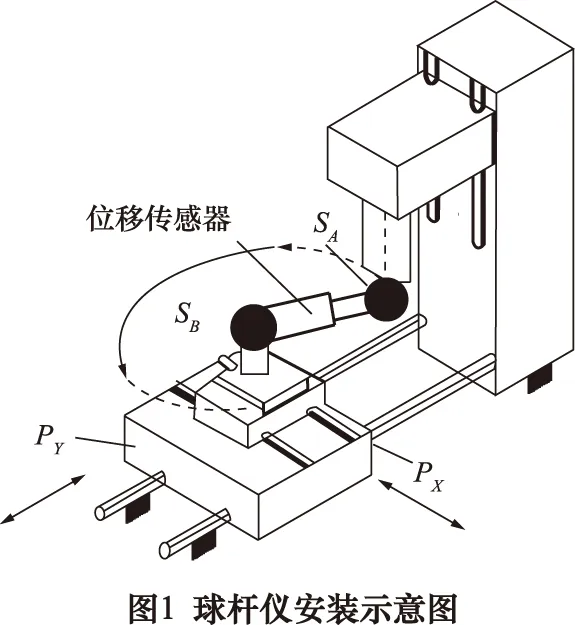
球杆仪安装后,在测试运动过程中,共有13个参数,其中有9个是机床固有及球杆仪安装产生的结构参数,为l0~l3,α12、α23,θ1~θ3。
如图2所示,l0和θ1对应球心SA的位置和方向,l3和θ3对应球心SB的位置和方向,这4个参数由球杆仪安装定位确定。
机床装配精度决定了两轴夹角和公垂线距离。PZ轴和PY轴的夹角为α12,公垂线距离为l1,PY轴和PX轴的夹角为α23,公垂线距离为l2,θ2是l1和l2的夹角。
机床运动的输入参数即3个轴对应的移动副位移为dX、dY、dZ,球杆仪计算长度dAB输出球杆仪显示测量值。

假设固定坐标系为{Of,i0,j0,k0},根据各参数关系,得到闭环矢量图3,因此位移矢量方程为:
ROA+RAB=ROZ+RZD+RDY+RYC+RCX+RXB
(1)
其中,RAB是两球心间矢量;ROZ、ROD和RCX分别为三移动轴的位移矢量;ROA是过SA的矢量,且垂直于ROZ,RXB是过SB的矢量,且垂直于RCX;RZD是PZ和PY公垂线的矢量;RYC是PY和PX公垂线的矢量。
对式(1)移项并去模,则可以得到:
|RAB|=|ROB-ROA|=|ROZ+RZD+RDY+
RYC+RCX+RXB-ROA|
(2)

在坐标系中,各矢量可分别通过图2中参数表示,将由参数表示的各矢量坐标代入式(2)中求解,可得到球杆仪测量参数dAB的表达式为:
(3)
其中:
U=dYdXcosα23-dZdYcosα12+dZdXf4
V=dX(l1sinα23sinθ2-l0f3)+dY(l3sinθ3sinα23-l0sinα12sinθ1)-dZ(l2sinθ2sinα12+l3f6)
W=-l1l0cosθ1+l2l0f5+l2l1cosθ2+l3l2cosθ3-l3l1f2+l3l0f7
f1=sinθ3cosα23cosθ2+cosθ3sinθ2
f2=sinθ3cosα23sinθ2-cosθ3cosθ2
f3=sinθ1cosα23sinα12+sinθ1sinα23cosθ2cosα12
f4=cosθ2sinα23sinα12-cosα23cosα12
f5=sinθ2cosα12sinθ1-cosθ1cosθ2
f6=f1sinα12+sinθ3sinα23cosα12
f7=f2cosθ1+f1cosα12sinθ1-sinθ3sinα23sinα12sinθ1
(4)
加工中心三轴运动均为误差运动,所以球杆仪测量数据包含各轴运动误差和式(4)中计算的理论值。
1.3 参数求解优化模型
式(4)通过矢量方程的求解创建了三轴加工中心测量过程中,球杆仪测量参数与其他12项参数间的关系,参数中包含球杆仪安装位置误差与各轴运动的方向和位置误差,可通过创建运动学优化模型求解最优结构参数值,进而分析三轴加工中心误差。


(6)
其中:参数W值与式(4)相同。

2 测量轨迹设计与误差分析
2.1 三轴联动测量轨迹设计
目前通常采用两轴联动圆轨迹测量,三轴联动轨迹尚无推荐,如采用两两联动构成1个圆轨迹与2个半圆轨迹组合形式测量三轴加工中心,则球杆仪扫略空间仅限于工作空间中间部分,对机床加工整体性能反应不充分。结合球杆仪结构特点,三轴联动测量轨迹应具有以下特点,两球头间相对运动预设轨迹应为球面曲线,且轨迹应尽量避免死角与急转,以此减少冲击;应使三轴运动均具有往复行程,以此满足反向越冲的指标测测量需求;同时使各轴行程尽可能布满,使测量轨迹尽量布满工作空间。
综上,本文设计一种四叶螺旋线为测量轨迹,其方程为:
(7)
其中:r是球杆仪校准长度;dX、dY和dZ分别为三轴位移;(cX,cY,cZ)为球心SA坐标,ξ∈(0,2π)为时变函数。测量轨迹如图4所示。

2.2 误差分析
将2.1节中轨迹及相应测量结果代入数学模型(5)中,可求解出9个最优结构参数,在此基础上可分析加工中心各项误差。其中:PY和PZ两轴间垂直度误差为α12-π/2;PX和PY两轴间垂直度误差:α23-π/2;PX和PZ两轴间垂直度误差:arccos(cα12cα23-sα12cθ2sα23)-π/2。
设单轴换向前运动的平均误差为ΔdX+(ΔdY+或ΔdZ+),换向后运动的平均误差为ΔdX-(ΔdY-或ΔdZ-),换向处运动误差峰值为maxΔdX(max(ΔdY)或max(ΔdZ)),则三轴反向越冲分别为maxΔdX-ΔdX-,maxΔdY-ΔdY-,maxΔdZ-ΔdZ-;;反向间隙分别为ΔdX--ΔdX+,ΔdY--ΔdY+,ΔdZ--ΔdZ+。
比例不匹配可通过给定比例系数二次优化求解,设三轴比例系数分别为a、b、c,令输入参数dX=a×dX、dY=b×dY、dZ=c×dZ,代入式(5)中优化。则三轴两两间分别比例不匹配分别为2r(a-b)、2r(b-c)、2r(c-a),其中r为机床圆测试半径。
3 实例验证
实验室选取某三轴立式加工中心机床进行对比验证,两轴联动方法和本文设计的三轴联动方法测量的结果如图5。

将三轴测量结果代入式(5)中,优化得结构参数最优解见表1。

表1 优化结构参数
按2.2节中误差分析方法,得到两种测量方法下三轴加工中心误差分析结果,对比如表2。
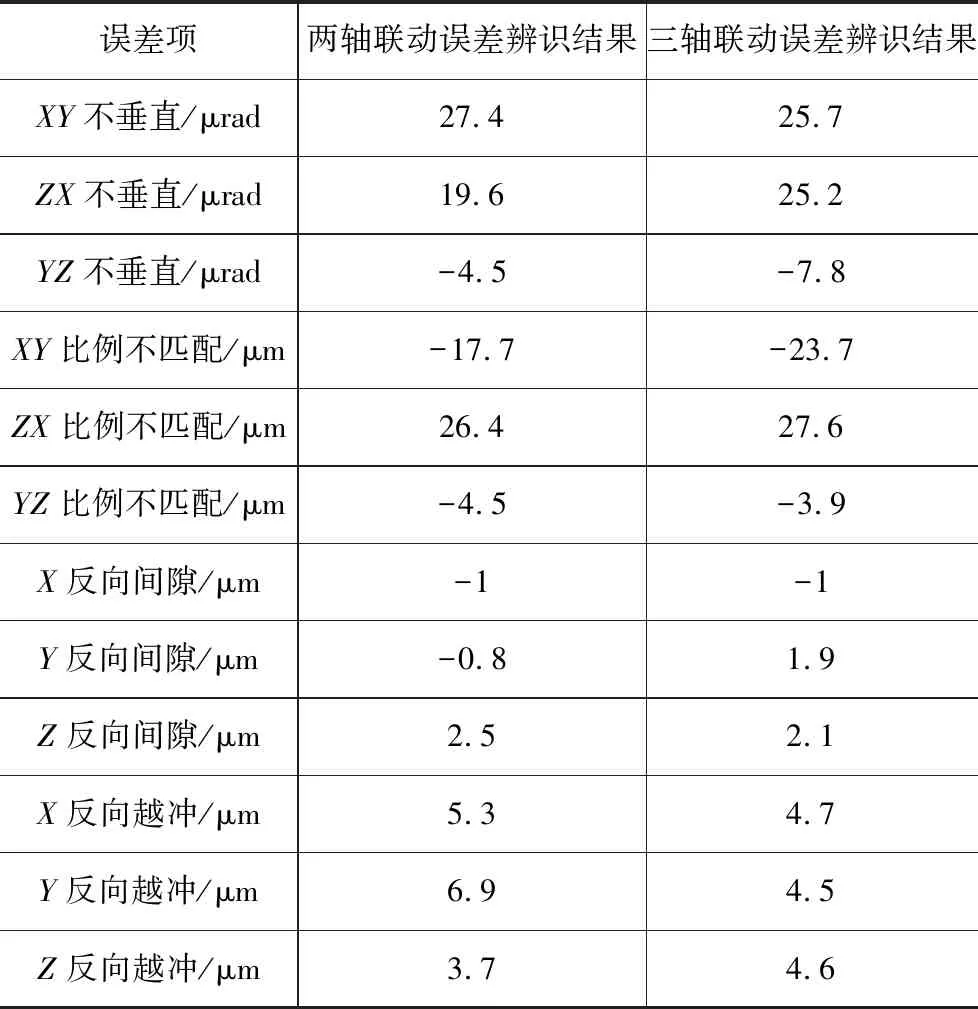
表2 误差分析结果对比
对比上述结果,结合机床结构特性,可知两种测量方法结果差距不大,可以确定本文方法的实用性,即通过一次测量有效辨识三轴误差。
4 结语
本文建立了球杆仪测量三轴加工中心运动分析模型,并设计四叶螺旋线为空间测量轨迹,通过优化方法有效求解机床三轴方向偏差与位置偏差,并给出误差数据分析方法,可以有效辨识三轴机床运动时比例不匹配、反向间隙、反向越冲和垂直度等误差。最后通过实例验证了该方法的有效性。
在实际应用中,可通过单次测量获取3个移动轴联动的全部误差,有效提升测量效率,对促进企业生产具有积极意义。

