Rockafellar乘子方法在元素测井解谱中的应用*

于 静，王振林，白晓伟

（1．中国石油大学（北京）克拉玛依校区 文理学院，新疆 克拉玛依834000；2.新疆油田勘探开发研究院，新疆 克拉玛依834000；3.新疆油田公司应急抢险救援中心，新疆 克拉玛依834000）

1 研究背景

随着勘探开发技术的日益成熟，页岩油气、致密油等非常规油气已经成为当今勘探开发的研究热点。而储层矿物含量的精确计算对于评价储层的物性、含油性、脆性、烃源岩特性（图1为实测的矿物成分与烃源岩有效性的关系图）及指导压裂具有非常重要的意义[1]。非常规油气储层，大都岩性多变，矿物组成复杂，储层评价难度大，仅仅依靠常规测井技术很难进行正确的储层评价。因此正确识别矿物及准确计算矿物含量是目前非常规油气储层研究面临的主要难题之一。

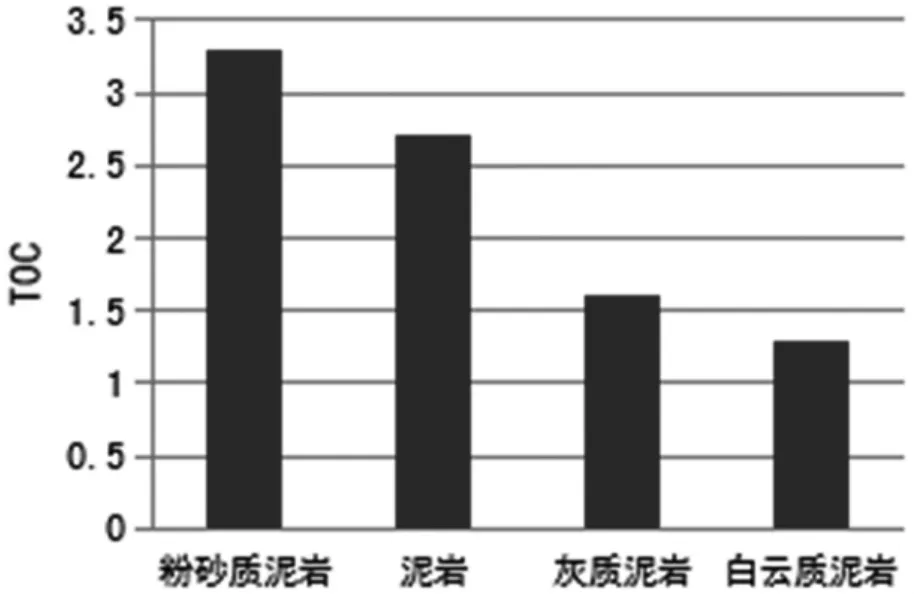
图1 烃源岩与矿物成分相关关系图

尽管地层中被发现的元素有近百种，但是其中氧、硅、铝、铁、钙、钠、钾、镁、氢等9元素却占据了地层总质量的98%以上[2]。类似地，岩石中已发现上千种矿物，但是在非常规油气储层中的常见矿物不过十余种。因此利用可以确定地层元素含量的伽马能谱测井，相对准确地评价地壳岩石中的矿物种类和含量变成了可能。

元素俘获测井是确定矿物含量和岩性识别最有效的测井技术之一。当前比较先进的元素测井是斯伦贝谢的ECS测井。其原理为仪器（图2）中子源产生快中子，快中子进入地层后，同地层中所含元素的原子核发生作用，作用释放出伽马射线[3-5]。每种元素产生特定能量的特征伽马射线，其计数率与元素的含量成正比。我们记录这些伽马射线形成的伽马能谱（图3），用实验室记录的每种元素标准伽马能谱（图4）[6]与之做对比，然后采用合适的解谱技术，利用恰当的氧闭合模型和聚类因子等方法得到地层常见元素的含量，进而计算出地层中所含的主要矿物含量（图5为元素测井谱处理的流程图）。

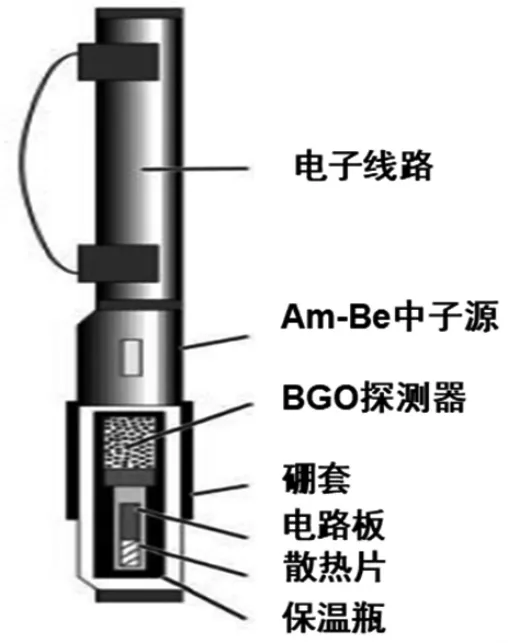
图2 ECS测井仪器结构示意图

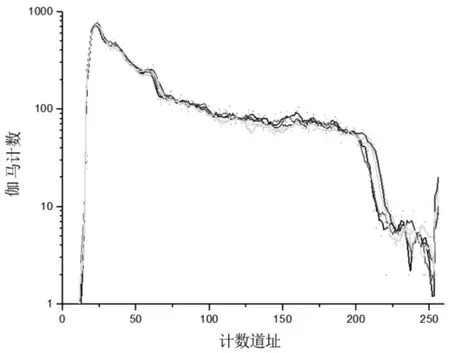
图3 实测伽马能谱图

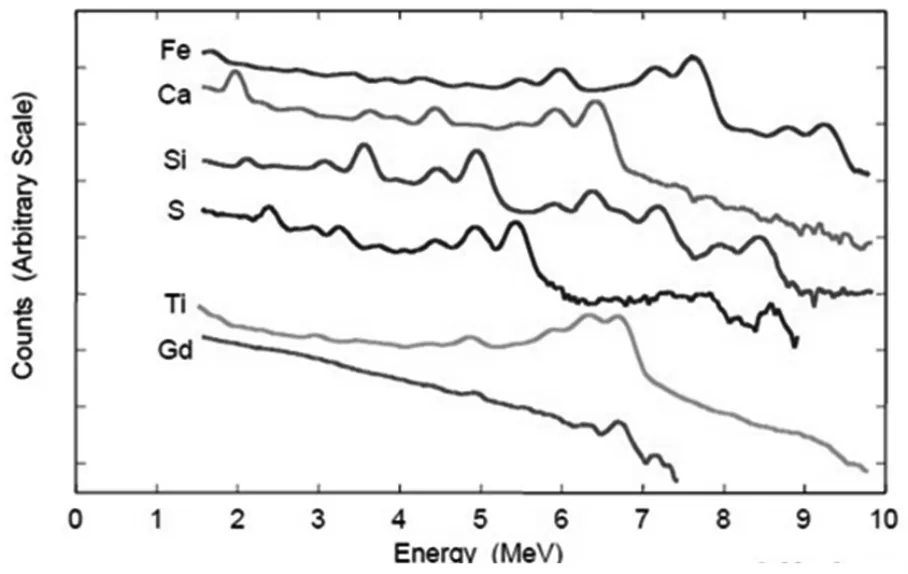
图4 各元素的标准谱

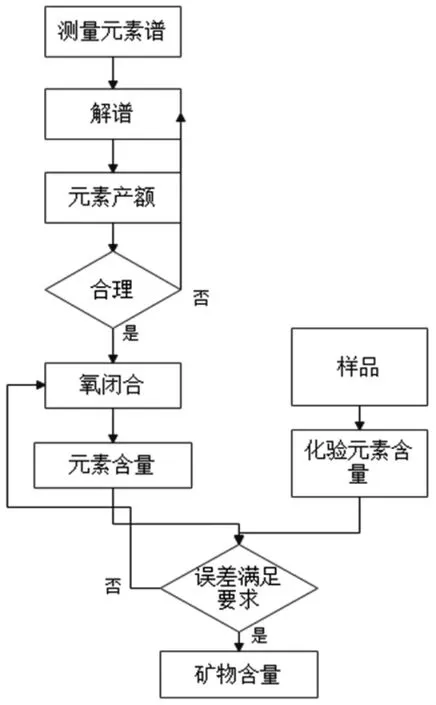
图5 元素测井谱处理流程

2 元素产额的确定

ECS记录的能谱是全部元素的伽马能谱（计数）的叠加，所以如果要得到准确的矿物含量，就必须对原始伽马能谱采用合适的方法进行解谱，进而得到每个元素对该谱的相对贡献，我们称这种贡献为元素的产额[7-8]。

在确定元素的产额时目前流行的是用最小二乘法进行谱数据处理。图6最右边道为最小二乘法解谱得到的镁元素的产额。我们将整个伽马能谱划分成为m个能量道，假若本地区有s个元素对此能谱有贡献，所以我们有如下关系式：

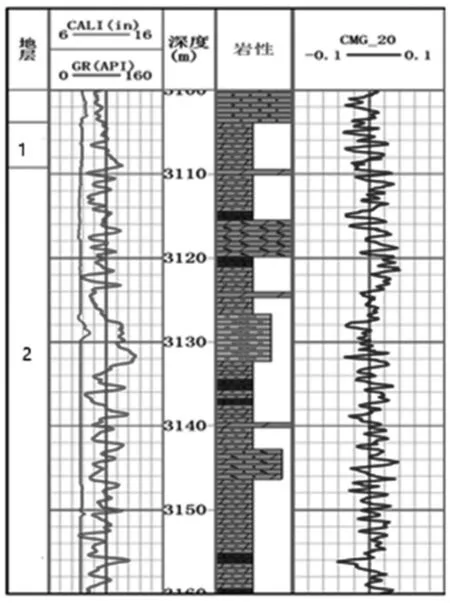
图6 J井最小二乘法得到的Mg元素产额

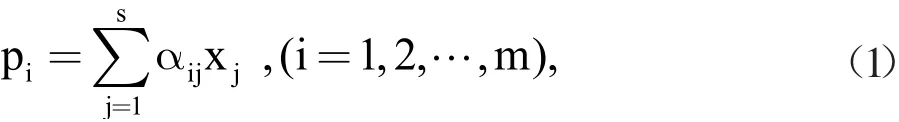
其中，pi是指所处理的伽马能谱的第i个能量道的计数率；αij指的是指测井仪器对第i道的第j种元素的响应系数；xj为待求的第j种元素对测量谱的相对贡献，即产额。

公式（1）包含了m个s元方程，即

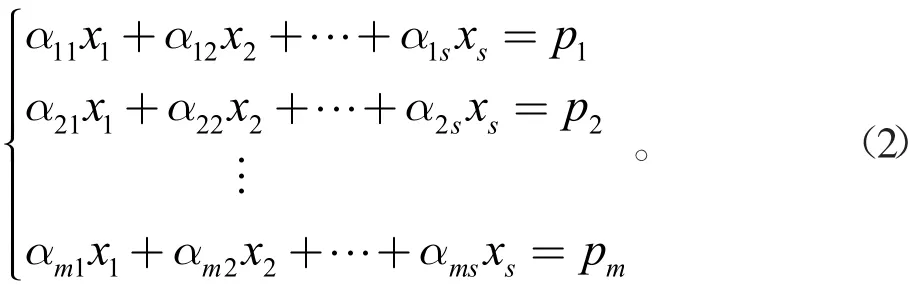
一般来讲，这是一个超定的方程组（公式的各数大于未知数的个数），其中每个pi均包含统计误差。为了求解xj，人们一般采用最小二乘法解决此问题，即得到最小二乘解

但是，在实际测量的伽马能谱中，因为大多数元素的特征伽马射线集中于高能部分，但是高能部分伽马计数往往较低，对于元素含量的确定非常不利，因此，我们用加权的最小二乘方法解决此问题。令达到最小。其中，ωi为权重因子，令

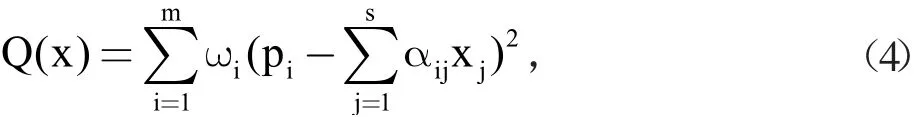
但是在用加权的最小二乘法处理实际ECS数据时，由于数据受温度、仪器误差及自然放射性等的影响，不可避免地将产生负值[8]（见图6）。为了解决这个问题，我们采用Rockafellar乘子算法[9-13]。

3 Rockafellar乘子算法数学原理

Rockafellar乘子算法是解决约束最优化问题的常见方法，它的基本思想是借助罚函数把约束优化问题转化为无约束优化问题，进而使用无约束优化方法来求解。具体做法如下：

为求解问题（4），我们首先引入松弛变量zj（其中j=1，2，…，s）将不等式约束转化为等式约束，将约束条件化为

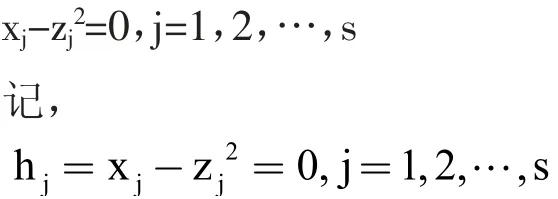
问题（4）转化为等式约束的最优化问题：

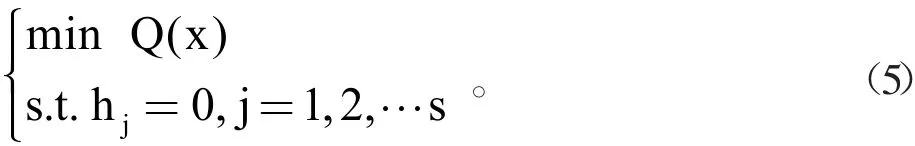
其次，考虑在等式约束下的增广Lagrange函数：

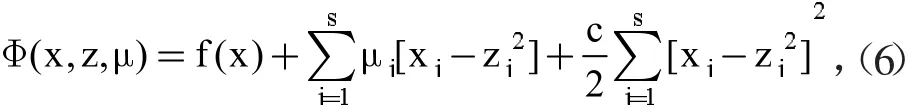
其中，μ（jj=1，2，…s）为拉格朗日乘子为惩罚因子。

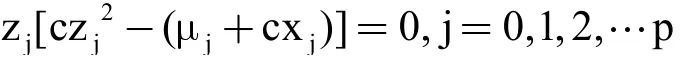
若μj+cxj≤0，则

因此，

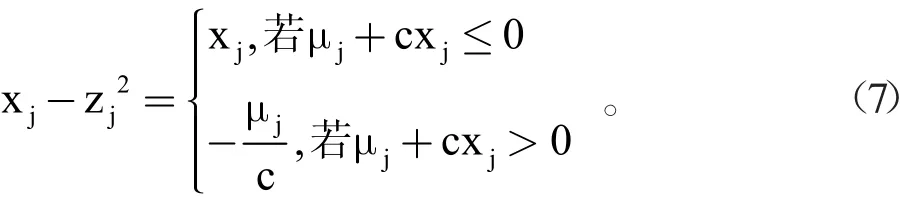
于是，当μj+cgj（x）≤0时，有：

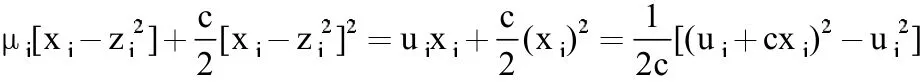
当μj+cxj>0时，有：

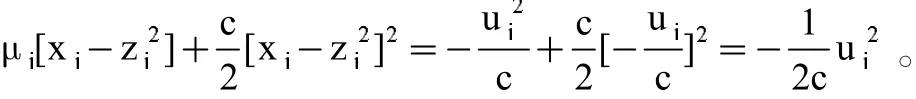
所以，得到乘子的迭代公式为

具体步骤如下：

（1）给定初始点x(0)及初始乘子μ(0)，给定精度ε，取c>0；

（2）以x(k-1)为初始点，求解minΦ（x，z，μ(k)），得到x(k)；

则x(k)为最优解，否则计算若β≤0.25，转到第4步，否则，令c=2c，转到第4步；

（4）计算μj(k+1)=μj(k)+chj（x(k)），k=k+1返回第1步。

4 Rockafellar乘子算法解谱实例

图7 为利用Rockafellar乘子算法计算某井的元素产额与用最小二乘法解谱得到的元素的产额对比图。从图7中可以看到，乘子算法的结果很好地解决了最小二乘法元素产额负值的问题，为后续矿物的反演及储层评价奠定了良好的基础。

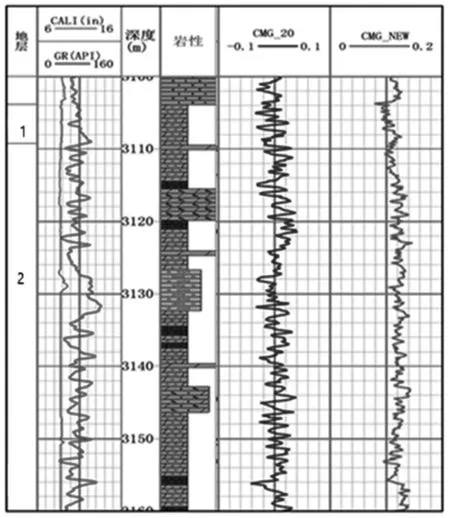
图7 J井乘子算法（最右道）与最小二乘法解谱对比图