无人机数据链带内连续波电磁干扰效应研究

许彤， 陈亚洲， 王玉明， 赵敏

(陆军工程大学 石家庄校区 电磁环境效应重点实验室，河北，石家庄 050003)

随着电磁战概念的日益兴起，复杂电磁环境下通信装备的电磁环境效应成为了广泛关注的问题[1-2]. 数据链属于武器平台信息化的产物，它将战场上的作战要素连成一个有机整体，既是现代信息化战争的基石，也是电磁战攻击的重点目标[3-4]. 由于中远程无人机造价高昂，且具有“敌近我远”的工作特点，数据链作为无人机搭载的通信设备，确保其在复杂电磁环境下的可靠性和稳定性非常重要.

作为典型的用频装备，数据链设备对信号频率的选择性较强，对于频率范围处于带内的干扰信号具有很高的接收灵敏度，因此容易受到带内干扰的影响；而对于处于在带外的电磁信号，则需要较高的功率才能使其受扰[5]. 目前数据链的电磁干扰效应的研究主要集中在单频连续波[6-7]和强电磁脉冲干扰[8-9]的电磁效应试验、作用机理以及防护方法等方面，对多信号叠加产生的电磁效应研究还比较少. 本文以当前部队应用最为广泛、技术较为成熟的某型中程通用无人机系统为研究对象，基于前门耦合电磁干扰效应，采用从数据链射频前端等效注入的方法进行电磁敏感度效应试验，对单频和双频电磁干扰对数据链的作用规律进行了研究，重点研究了连续波干扰信号对接收机性能和指标参数的影响，得到的研究结果为用频装备在复杂电磁环境下的机理研究和适应性评估提供了依据.

1 电磁干扰前门耦合与数据链工作原理

1.1 前门耦合理论

通常情况下，外界电磁辐射干扰可能通过“前门”或者“后门”耦合路径影响用频装备，本文研究对象是一种搭载在中型无人机上的数据链设备，内部屏蔽措施相对较为完备，因此前门耦合是其最主要的干扰耦合方式[10]. 在只考虑前门耦合的情况下，表征机载天线接收到的干扰信号功率Pjr[11]为

(1)

式中：Pj为干扰源的发射功率；Gj、Gr分别为干扰源和机载天线的增益；Rj为无人机和干扰源的距离；λj为干扰信号波长；μj为天线之间的极化匹配因子. 若在一定的工作信号强度下，数据链的干扰容限为Pr，则根据实现有效干扰的功率准则，当Pjr≥Pr时，数据链通信受扰.

假设两个连续波干扰源S1、S2同时存在，如图1所示. 无人机地面控制站所在位置为O，无人机A沿固定航迹执行任务. 假设干扰源采取跟踪干扰的模式，当S1、S2分别单独开机工作时，无人机通信性能受到干扰的边界为分别以S1C、S2E为半径，底面为球面的锥形区域；当两个干扰机同时开启时，相比单一频率的干扰源，多个干扰叠加后可能会对数据链设备产生新的干扰效应[12]，从而使数据链的干扰容限降低，此时对无人机产生有效干扰的边界可能会前移至弧BD，在较远的距离下就造成数据通讯扰乱、中断，甚至射频前端损伤. 本文以此为假设开展研究和验证.

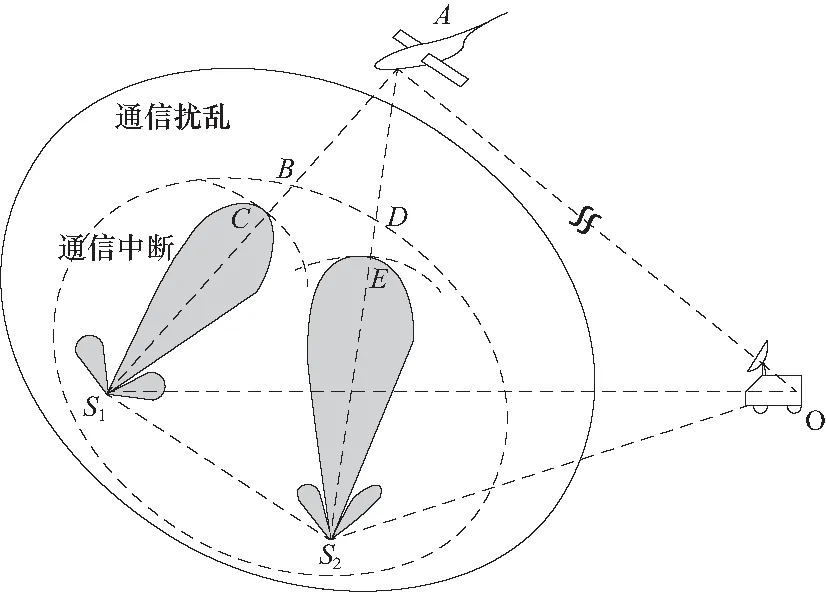
图1 无人机数据链电磁干扰边界示意图Fig.1 Scenario of a UAV radiated byelectromagnetic interference

1.2 数据链工作原理分析

天线接收空间辐射场能量并进行电信号的变换，如图2所示. 工作信号混合干扰信号通过具有滤波作用的双工器后，进入混频与中频放大单元. 信号流经过前端低噪声放大器、滤波器后与本振信号进行下变频混频，再经自动增益控制(automatic gain control,AGC)电路将中频信号的幅值稳定在一定区间. 稳幅、滤波后的中频信号yIF进入中频处理模块，再一次下变频至零中频后进行A/D变换，得到的数字信号进行解扩、解调和纠错译码[13].

图2 数据链接收机原理图Fig.2 Scheme of data-link receiver

数据链使用BPSK直接序列扩频(direct sequence spread spectrum，DSSS)的调制方式. 假设数据链受到的来自不同方向、不同强度、不同频率的若干个连续波电磁干扰为Ji(t)，则天线接收到的数据链工作信号s(t)、总干扰信号J(t)和噪声n(t)分别为

s(t)=Usd(t)p(t)cos(ωct+φc)

(2)

(3)

n(t)=nc+jns

(4)

式中：Us、Uji分别为工作信号和干扰信号的电压幅值；d(t)为数据调制波形；p(t)为扩频波形；ωc为载波中心频率；Δωi为干扰信号与工作信号之间的频偏；φc、φji分别为工作信号和干扰信号的相位；nc、ns分别为噪声信号的正交分量. 因此，由天线接收到射频前端的信号y1(t)为

y1(t)=s(t)+J(t)+n(t)

(5)

射频前端设置多级低噪声放大器(low-noise amplifier, LNA)和带通滤波器，低噪放增益的选频特性与频率相关，设低噪放对工作信号、干扰信号和噪声信号的放大倍数分别为ks、kji和kn. 在较短的时间间隔之内，滤波器的频率响应可以用具有脉冲响应h(t)的时不变滤波器表示，则滤波后的干扰信号为Ji′(t)=Ji(t)*h(t). 因此天线接收的信号经过放大和滤波之后为

(6)

放大、滤波后的信号经过混频器进行下变频处理，设本振信号为yLO=ULOcosωLOt，ULO为本振信号幅值，ωLO为本振频率. 变频处理后的信号通过滤波器滤除杂散频率为

y3(t)=y2(t)yLO(t)=

(7)

将式(2)～(4)代入式(7)，并且记yIF(t)为中频工作信号，yJ(t)为中频干扰信号，n′(t)为变频处理后的噪声信号.ωIF、ωJ分别为中频工作信号和干扰信号的频率，分别满足ωIF=ωLO-ωc，ωJ=ωIF-Δωi，得到

yIF(t)+yJ(t)+n′(t)

(8)

(9)

(10)

可以看出，经过检波后的中频信号中，除了包含工作信号之外，还存在频偏为Δωi的干扰信号yJ(t)和噪声信号n′(t)，当干扰信号功率足够大时，噪声信号n′(t)对于接收机的影响可以忽略不计.

由于混频器后使用的声表面波(surface acoustic wave，SAW)滤波器带宽为ωs，具有低损耗、高可靠性的优点，器件体积和重量相较陶瓷介质滤波器具有明显的优势，但其通带通常较宽，导致选频特性较差，当Δωi<ωs/2时，干扰信号无法在中频被滤除，将会同工作信号一起通过AGC电路进行处理. 将式(8)简化表示为

y4(t)=Ain(t)y(ωt)

(11)

式中：Ain(t)为AGC输入的电压幅值；y(ωt)为工作信号和干扰信号的函数. 由式(8)和式(11)可知，y(ωt)中除了中频工作信号之外，还含有频率为ωJ的干扰信号. 则经过AGC稳幅处理之后的中频信号为

yIF(t)=Aout(t)y(ωt)=g(Ain,Vc)y(ωt)

(12)

式(12)中，Aout=g(Ain,Vc)为常数，其中Vc为反馈电压值，它通过改变函数g(Vc)来调节AGC增益，从而获得所需的电压输出Aout. 可以看出，AGC模块的稳幅处理没有选择性，工作信号将会和干扰信号一同获得一定的增益，此外，由于SAW滤波器不能将临近中心频率的干扰信号yJ(t)滤除，这导致干扰信号进入解扩解调单元，干扰后级的解调和译码过程，从而造成通信性能显著降低.

中频信号yIF(t)经过解扩后的能量计算单元进行信号能量和噪声能量的统计，从而获得接收机基带处理部分的信噪比(signal noise ratio, SNR). 解扩后的信号通过VB译码单元，将viterbi译码后的数据进行再一次卷积编码，与译码之前的数据进行比对，得到了信道的统计误码率(bit error ratio, BER). 译码处理之后，数据帧进行同步过程，数据发送端在信息流中插入一段固定的码组作为每帧的头尾标记，接收端对这些码组的位置进行判别，实现帧同步. 当接收机不能识别信息帧的帧头时，接收机判定链路失锁，并将状态传输至地面端软件进行显示.

电磁干扰的存在会影响信号的相关检测过程，因此造成信噪比降低，误码率会随之增加，在实际应用中表现为地面控制指令传输出现误操作. 随着干扰信号功率的增加，当影响到接收机的帧同步时，数据链表现为失锁，此时机载数据链不能和地面站保持数据传输的同步，无人机处于失控状态. 由于误码率是通信系统可靠性的度量，常用于评价干扰信号对数据链的干扰效果[14]，失锁也是表示数据通信状态的定性标志，因此在通信设备的敏感度实验中，通常采用的定量和定性判据分别是误码率和失锁.

1.3 干扰效应试验设计

经过天线到射频前端是通信装备带内干扰的主要耦合途径，因此可以采用从天线端口等效注入的方法对数据链进行效应试验，一方面便于分析带内干扰在接收机内部的耦合路径，另一方面可以排除电磁环境扰动对试验结果的影响. 试验配置如图3所示，分为4部分：机载数据链设备、地面数据链设备、干扰注入模块和模拟无线通信信道. 机载数据链设备和地面数据链设备之间通过射频线缆相连，为了确保大功率的工作信号不会损坏射频前端，在有线链路上串接了两个40 dB的固定衰减器. 另外可以通过调节衰减器的衰减量改变链路上的信号强度，模拟无人机飞行过程中工作信号的变化. 干扰信号由信号源产生，通过多通道合路器将干扰信号和工作信号合路后注入到上行链路中，对上行遥控链路进行干扰. 地面站设备和监测计算机之间通过网线相连，可以从监测软件上读取数据链的工作状态和各项性能参数.

图3 干扰信号注入实验配置图Fig.3 Configuration of Interference injection experiment

2 单频干扰效应试验

2.1 试验判据的选取

密集的用频装备和激烈的电子对抗构成了战场复杂电磁环境，现有的有意通信干扰信号形式包括载波干扰、噪声干扰、调制干扰和脉冲干扰等，其中时域上连续的干扰均可视为由多个连续波叠加组成. 单频连续波干扰作为一种最简单的干扰形式，具有容易模拟且频率单一、功率集中的特点，能够反映用频装备对不同频率电磁辐射敏感的基本属性，揭示其电磁辐射效应的基本规律[15]. 为研究误码率和失锁两种判据之间的关联性，选择合适的判据. 在数据链通信频带内选取3个典型频率进行单频干扰注入试验，结果如图4所示.

图4 不同单频干扰频率下误码率随干扰信号功率的变化Fig.4 Variation of BER under different single-frequency interference frequencies

同频和临频干扰时，随着干扰信号的增强，信道误码率明显增大，当误码率达到2×10-2后开始发生帧失步现象，继续增加干扰强度则数据链失锁. 同频干扰失锁时的误码率和干扰强度均低于临频干扰，但当干扰频率位于通信频带边缘，误码的增长率迅速提高，随着干扰信号强度的增加，误码率发生突变，以本文所用的数据链为例，当干扰频率距离中心频率±5 MHz时，误码率达到1.5×10-2就发生失锁现象. 从产生误码到完全失锁，干扰功率只增加了1 dB，这就给观测误码变化造成了困难. 因此，对于数据链通频带内的电磁干扰实验，采取失锁作为判据，能够更加稳定、直观地反映受扰现象.

2.2 单频电磁干扰失锁阈值

选取不同工作信号强度进行电磁干扰效应试验，测得不同干扰频率下数据链的失锁阈值，如图5所示，P为失锁时的干扰阈值，Δf为干扰功率与数据链工作信号中心频率的偏差. 在同一工作信号强度下，以工作信号频率f0为中心，失锁阈值曲线大致呈现“U”型. 干扰信号与工作信号频率越相近，干扰阈值越低；干扰频率与工作信号的偏差变大时，干扰阈值会逐渐增大. 需要特别指出的是，当干扰信号频率位于工作信号中心频率f0处时，干扰阈值并非最低，而是高于f0+1 MHz处的干扰阈值，差值约为1.5 dB. 这是由于扩频码具有平衡性，在一定程度上能够抑制载波泄露，因此和非同频干扰相比，当施加同频干扰信号时，干扰信号在接收终端会受到更大的衰减，达到失锁状态需要的功率值也略高于临频干扰.

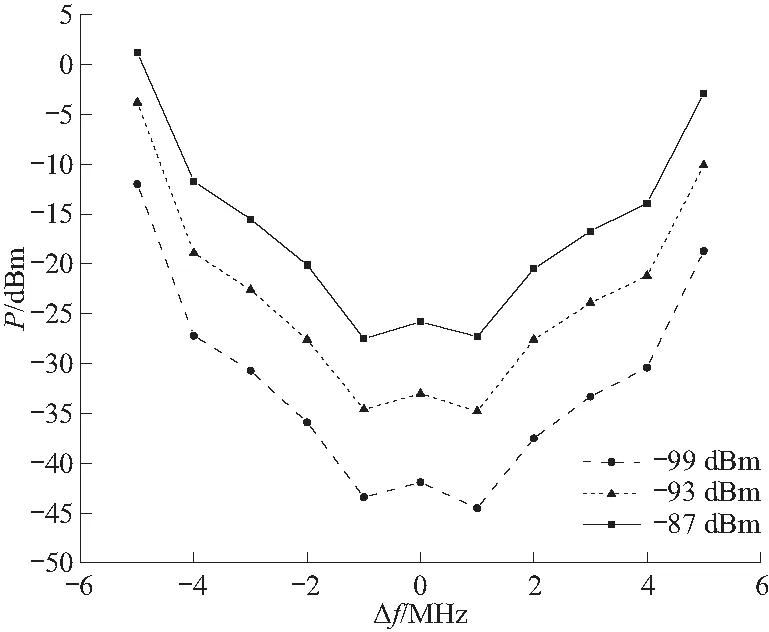
图5 不同工作信号强度下单频干扰失锁阈值Fig.5 Thresholds of single-frequency interference when the lost-link occurs with different working signal intensities

信噪比是表征接收机数据终端通信性能的核心参数之一，是通过积分清零滤波器对工作信号和噪声信号分别累积后求得的比值. 以失锁时的功率值为准线对信噪比进归一化，干扰功率和失锁阈值的差值为ΔP. 以干扰功率为f0、f0-2 MHz、f0-5 MHz为例，由图6所示，信噪比随干扰功率的增加呈现线性下降趋势，在同频干扰的情况下，失锁时的信噪比最大，约为6；非同频干扰的情况下，信噪比在1～2附近即通信中断. 频率距离中心频率f0越近，失锁时的信噪比越高，随着干扰功率的上升，信噪比下降越快.

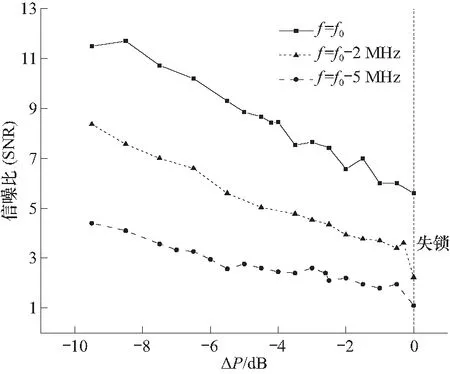
图6 不同干扰单频干扰频率下信噪比变化趋势Fig.6 Variation of SNR under different single-frequency interference frequencies

2.3 射频前端单频干扰效应分析

在输入信号较小时，接收机系统可近似看作是一个线性系统，当输入信号幅度超过某一限值，系统逐渐显现出非线性，这种非线性效应会造成一系列的影响，主要包括谐波、增益压缩、阻塞、交调、互调等. 为研究数据链产生失锁效应的具体原因，试验测试了在施加干扰的状态下数据链失锁时输出的中频信号.

无干扰状态下的中频输出波形如图7所示，在正常工作状态下射频前端对工作信号进行放大处理. 接收机前端接收到来自天线的工作信号fc的峰值功率约为-44.5 dBm，经过接收机滤波、放大后的中频输出信号f0的峰值功率大约为-20.5 dBm，此时射频前端的系统增益为24 dB.

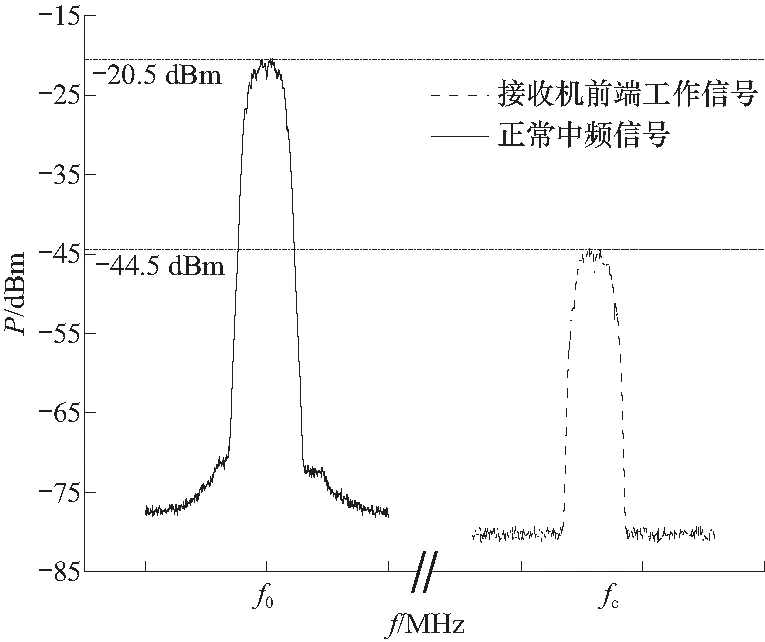
图7 无干扰时射频前端的输入输出信号Fig.7 The input and output signals of the RF front-end without interference

对数据链施加单频干扰，得到不同干扰强度下的中频输出信号，如图8所示. 对比试验结果发现：随着干扰信号频偏的增大，干扰功率阈值逐渐上升，造成数据链失锁时对应的中频工作信号增益明显降低. 当干扰信号频率接近接收机通带边缘时，对比输入时的工作信号功率包络峰值-44.5 dBm，干扰后的中频信号为-46.5 dBm，工作信号没有被放大而是受到了压缩，压缩幅度约为2 dB. 失锁时对应的工作信号峰值明显低于无干扰时的中频输出信号.

图8 不同频率单频干扰下中频输出信号Fig.8 IF output signal under single-frequency interference with different frequency

在f0-4 MHz和f0-5 MHz的干扰下，产生失锁效应时输入到接收机的干扰信号大小分别为-39.4 dBm和-55.7 dBm，相差16.3 dB，而通过测量中频信号发现，中频工作信号的功率包络基本一致，其峰值约为-46.5 dBm. 主要原因是在AGC电路的作用下，尽管干扰信号功率随着频偏的增大而增强，但此时工作信号功率基本已经被压制到最低. 对比图6中信噪比和图8中的中频信号发现，随着干扰频偏的增大，失锁时的中频工作信号功率产生压缩效应，从而导致失锁时的信噪比下降.

3 双频干扰效应试验

3.1 双频电磁干扰失锁阈值

数据链工作的中心频率为f0，双频干扰频率分别为f1、f2，均位于数据链工作频带内，功率分别为P1、P2. ΔP1、ΔP2分别为两个频率下干扰信号功率与单频失锁功率之间的差值，试验配置如前文中图3所示. 选择两组典型频率进行带内干扰失锁阈值分析：一种情况是f1为同频带内干扰，f2为非同频干扰；另一种是两个频率都是非同频带内干扰.

试验结果如图9所示，和单频干扰失锁阈值曲线图5类似，双频干扰的阈值曲线也呈现“U”型. 在f1为同频干扰，f2为非同频干扰的情况下：当f2位于中心频率f0±4 MHz以内时，两个干扰同时存在时的失锁阈值均低于只有一个单频干扰情况下的阈值，并且数据链在频率组合为f1=f0,f2=f0+1 MHz时最为敏感：当试验施加f1的功率比单频失锁功率低1 dB，即ΔP1=-1 dB时，P2比单频失锁阈值低9.9 dBm. 当f2位于通信敏感带宽边沿，即f2=±5 MHz时，随着P1的下降，P2的变化不明显，且基本与单频干扰的阈值相同，说明此时的失锁效应主要由位于带宽边沿的干扰功率P2决定，同频干扰f1在失锁功率上并没有起到明显的干扰效应叠加作用.

图9 当f1为不同功率的同频干扰时f2的失锁阈值曲线(f1=f0)Fig.9 Thresholds of dual-frequency interference when f1=f0 with different power

f1=f0-2 MHz时的情况和f1=f0相似，由图10可以看出，当两个干扰频率均处于带内且都不是中心频率时，f0±4 MHz以内的双频干扰对应的干扰阈值均低于单频. 施加f1的功率比单频失锁功率低1 dB时，P2低于单频阈值的现象最为明显，特别是当ΔP1=-1 dB，f2=f0+1 MHz时，P2比单频阈值低12.4 dB. 当f2位于数据链通频带边缘，即±5 MHz时，P1的降低对P2的变化没有影响，双频干扰导致失锁时的P2值与单频失锁时的数值相同.

图10 当f1为不同功率的非同频干扰时的双频失锁阈值(f1=f0-2 MHz)Fig.10 Thresholds of dual-frequency interference when f1=f0-2 MHz with different power

综上所述，在距中心频率±4 MHz以内的双频干扰作用下，数据链达到失锁阈值时每一个干扰源的功率均低于只施加单一干扰源时的情况，说明多个带内干扰信号相互叠加，能够增加干扰源的共同作用范围，在更远的作用距离上对数据链造成威胁. 而当干扰信号频率距离中心频率±5 MHz时，由于干扰信号频率位于射频前端通频带边缘，链路衰减较大，因此需要施加较大的功率才能使数据链受到干扰，且双频信号对失锁效应的叠加作用并不明显.

3.2 射频前端双频干扰效应分析

对比单频干扰试验的效应现象，针对在双频带内干扰下的射频前端输出，选取4组干扰频率组合：(f0,f0-2 MHz)、(f0,f0-4 MHz)、(f0-2 MHz,f0-4 MHz)和(f0+1 MHz,f0-2 MHz)进行效应分析. 根据2.3节中对单频干扰时中频输出信号的分析，得到数据链产生失锁效应的原因主要是由于AGC放大器作用使工作信号产生了增益压缩，为观察在双频干扰作用下中频信号的输出和单频有何异同，对双频干扰条件下数据链输出的中频信号进行了测试，结果如表1所示.Pi0为中频工作信号功率包络的峰值，Pi1、Pi2分别为干扰信号f1、f2经过射频前端后输出的信号功率峰值，Pi是输出中频信号总功率.

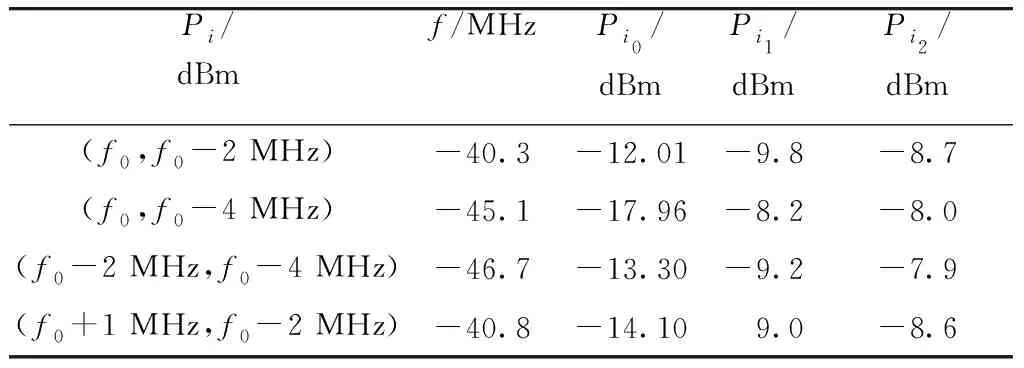
表1 典型双频干扰条件下中频信号功率Tab.1 IF signal power of tipical dual-frequency interference

由表1可知，无论干扰输入如何变化，由于AGC的限幅作用，中频信号总功率保持在-8 dBm左右，干扰信号频偏或功率的改变并不会导致中频输出总功率的大幅度变化；在使数据链失锁的干扰信号组合中，频偏更大的信号f2的干扰功率更高，因此输出的功率Pi2占总功率Pi的比重也最高；随着干扰信号频偏Δf的增大，达到失锁状态时的中频工作信号增益Pi0也随之降低.

以干扰频率组合(f0,f0-4 MHz)为例，将双频和单频干扰条件下数据链失锁时的中频工作信号进行对比，如图11所示.f1=f0、f2=f0-4 MHz分别单独作用下的中频工作功率分别为-37 dBm和-46 dBm，当干扰频率组合(f0,f0-4 MHz)共同作用时的中频工作信号输出约为-46 dBm，与只施加f2=f0-4 MHz干扰时的中频工作信号输出功率相等. 而对比图10中的失锁阈值可知，f1、f2分别单独作用下的失锁阈值为-17.6 dBm及-1.7 dBm，共同作用时的功率为-18.6 dBm及-3.4 dBm，均低于单频干扰下的失锁阈值. 因此与单频干扰相比，双频干扰时工作信号的增益主要受频偏更大的干扰信号影响，在功率更低的组合下就能使中频输出达到失锁时的限值.

图11 单频干扰和双频干扰导致数据链失锁时的中频输出信号(f1=f0,f2=f0-4 MHz)Fig.11 Comparison of IF output between single-frequency and dual-frequency interference when datalink lost-link(f1=f0,f2=f0-4 MHz)

结合2.3节对射频前端的分析可知，大功率的连续波干扰在接收机内会对AGC电路造成影响，导致工作信号产生增益压缩效应，但不同干扰功率下导致数据链失锁的中频信号功率并不相同，干扰频偏较小时，失锁时中频信号功率较高. 多个频率同时干扰接收机时，每个单频点只需要更低的干扰功率，就能够使工作信号压缩到失锁的功率包络以下，使数据链产生失锁效应.

3.3 通信性能参数分析

由前节可知，由于干扰信号进入接收机和AGC放大器的限幅作用，导致中频工作信号增益不足，从而使进入终端解扩解调处理部分的信号功率降低，然而在不同干扰频率组合下，导致数据链失锁的中频信号功率并非确定值，这说明失锁效应还与数据终端的解扩解调单元有关，此处主要关注数据终端的两个重要参数：信噪比和误码率. 为了方便对通信参数进行对比，以失锁时的功率为基准对干扰功率进行归一化，观察数据链系统在临近失锁6 dB之内的性能参数变化规律.

3.3.1信噪比干扰效应分析

通信接收机解扩后的信噪比直接关系到载波和伪码跟踪的精度，从而对解调后的误码率产生影响. 图12～15中显示了在不同干扰频率组合下，ΔP1不同时，信噪比随着ΔP2的增大直到失锁的过程. ΔP1、ΔP2分别为两个频率下干扰信号功率减去单频失锁功率的差值，图中阴影部分标明了干扰功率距离失锁阈值1 dB时的信噪比变化情况.

图12、13分别为频率组合为(f0,f0-2 MHz)、(f0,f0-4 MHz)时的信噪比变化规律，可以看出，随着ΔP2的增大，信噪比基本呈现线性下降的趋势，直到距离失锁1 dB的范围内急剧降低；频率组合为(f0,f0-2 MHz)时造成失锁时的信噪比在1.5～2.5之间，频率组合为(f0,f0-4 MHz)时失锁的信噪比在1.5～2.0之间，略低于(f0,f0-2 MHz)时的信噪比；ΔP2相同的情况下，ΔP1越大，信噪比越高，并且在频率组合为(f0,f0-2 MHz)时，降低同频干扰功率，信噪比下降的幅度大于频率组合为(f0,f0-4 MHz)时的情况.

图12 双源干扰频率为(f1,f2)时，数据链信噪比在不同 ΔP1条件下随ΔP2的变化规律(f1=f0,f2=f0-2 MHz)Fig.12 Ralationship between SNR and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0,f2=f0-2 MHz

图13 双源干扰频率为(f1,f2)时，数据链信噪比在不同ΔP1条件下随ΔP2的变化规律(f1=f0,f2=f0-4 MHz)Fig.13 Ralationship between SNR and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0,f2=f0-4 MHz

图14描述了频率组合为(f0-2 MHz,f0-4 MHz)时信噪比的变化规律，在还未到达临界失锁状态时，随着干扰功率P2的上升，信噪比的变化呈现平缓的线性下降的趋势，并且P1的功率越低，信噪比随P2的增大下降得越快. 这是由于f1距离中心频率较近，当P1功率逼近失锁阈值时，对信噪比的影响占主体地位，此时P2对信噪比的影响较弱，而当f1功率下降，P2对信噪比的影响增强，信噪比随P2的变化才愈加明显. 图15描述了干扰源频率组合为(f0-2 MHz,f0+1 MHz)时数据链信噪比的变化规律，较为反常的是，当P1固定时，信噪比随P2的上升变化并不明显，直到距离失锁阈值1～2 dB时，此时信道质量急剧恶化，信噪比迅速下降到失锁限值.

图14 双源干扰频率为(f1,f2)时，数据链信噪比在不同ΔP1条件下随ΔP2的变化规律(f1=f0-2 MHz,f2=f0-4 MHz)Fig.14 Ralationship between SNR and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0-2 MHz,f2=f0-4 MHz

图15 双源干扰频率为(f1,f2)时，数据链信噪比在不同ΔP1条件下随ΔP2的变化规律(f1=f0-2 MHz,f2=f0+1 MHz)Fig.15 Ralationship between SNR and ΔP2under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0-2 MHz,f2=f0+1 MHz

结合图12～15和图6中单频干扰下数据链信噪比的变化趋势，可以得到：单频干扰和双频干扰信噪比变化趋势相似，均随干扰功率的增加线性减小，并在距离失锁阈值1 dB以内急剧下降；信噪比和干扰信号频率有关，干扰频偏越大，失锁时的信噪比越低；双频干扰导致数据链失锁时的信噪比低于只施加其频率组合中某一单频干扰的信噪比.

3.3.2误码率干扰效应分析

由于误码率是个统计量，在一段时间内会存在一定的波动范围，数值的稳定性较差，因此试验采取每200组数取平均值的方式得到最终的误码率数值. 通常在靠近中心频率的带内干扰，误码率随着干扰信号功率的增大而上升，到2×10-2以上时基本处于临界失锁状态.

图16、17分别显示了数据链受到频率组合为(f0,f0-2 MHz)、(f0,f0-4 MHz)的干扰时的误码率变化曲线，可以看出：随着干扰信号功率的增大，误码的增长呈现先慢后快的趋势；在ΔP1相同的情况下，干扰组合为(f0,f0-2 MHz)时的误码率高于频率为(f0,f0-4 MHz)时的误码率；当f2=f0-4 MHz时误码率随干扰信号功率上升的速度比f2=f0-2 MHz时更快，数据链需要达到较高的误码率才会失锁.

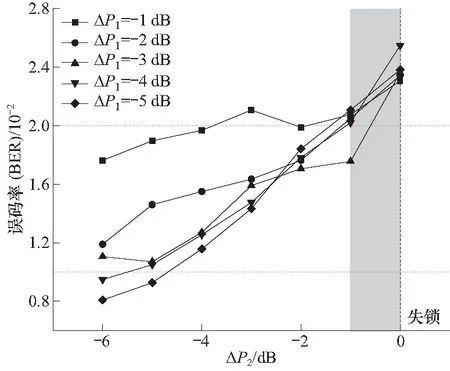
图16 双源干扰频率为(f1,f2)时，数据链误码率在不同ΔP1条件下随ΔP2的变化规律(f1=f0,f2=f0-2 MHz)Fig.16 Ralationship between BER and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0,f2=f0-2 MHz

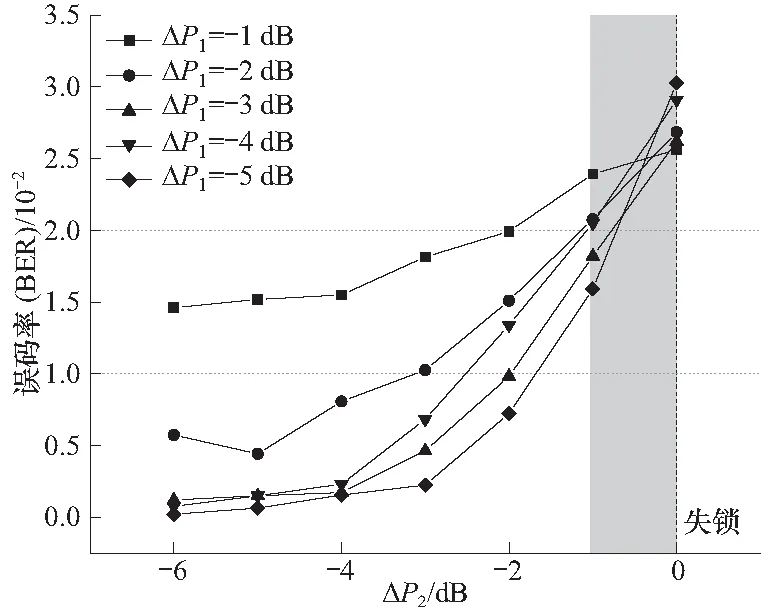
图17 双源干扰频率为(f1,f2)时，数据链误码率在不同ΔP1条件下随ΔP2的变化规律(f1=f0,f2=f0-4 MHz)Fig.17 Ralationship between BER and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0,f2=f0-4 MHz

图18、19分别描述了干扰频率组合为(f0-2 MHz,f0-4 MHz)、(f0-2 MHz,f0+1 MHz)时数据链误码率的变化规律. 误码率随干扰功率的增加呈现非线性上升趋势，从ΔP2=-6 dB到失锁，组合频率为(f0-2 MHz,f0-4 MHz)时的误码率增幅略大于(f0-2 MHz,f0+1 MHz)，且f2=f0-4 MHz时误码率整体低于f2=f0+1 MHz时的误码率. 根据图18、19，并结合图16、17中f1为同频干扰时的情况可以得出：在一个频率固定的情况下，另一频率的频偏越大，总体误码率水平越低，在失锁6 dB以内的误码率上升越快；数据链对于含有临频干扰的频率组合较为敏感，对于本文研究的数据链，在距离中心频率1 MHz频点处，较低的失锁阈值就能得相对较高的误码率.

图18 双源干扰频率为(f1,f2)时，数据链误码率在不同ΔP1条件下随ΔP2的变化规律(f1=f0-2 MHz,f2=f0-4 MHz)Fig.18 Ralationship between BER and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0-2 MHz,f2=f0-4 MHz

图19 双源干扰频率为(f1,f2)时，数据链误码率在不同ΔP1条件下随ΔP2的变化规律(f1=f0-2 MHz,f2=f0+1 MHz)Fig.19 Ralationship between BER and ΔP2 under different ΔP1 when the dual-frequency interference is (f1,f2),f1=f0-2 MHz,f2=f0+1 MHz

4 结 论

针对某型无人机数据链系统开展了单频和双频连续波的注入效应试验，确定了利用失锁阈值作为数据链电磁干扰效应的评价方法，得到了连续波带内干扰条件下的失锁阈值和通信性能参数变化规律. 需要指出的是，由于不同用频系统的编码方式、通信体制、数据帧结构等不同，通信链路失锁时的性能参数和功率阈值存在差异，但本文提供的试验方法和规律性结论具有参考意义. 具体结论如下：

① 当大功率干扰信号通过天线进入接收机时，接收机内部AGC电路增益降低甚至呈现出负增益的情况，导致工作信号的中频输出功率不足，从而影响数据终端对信息的解扩解调过程. 与单频干扰相比，双频干扰时工作信号的增益受频偏大的干扰信号影响更大，使中频工作信号压缩到可解调出工作信号的功率限值之下，在功率更低的组合下就能使数据链达到失锁状态，其中临频干扰的效应叠加现象最为明显.

② 在单频连续波干扰下，当干扰功率较低时，信噪比随干扰信号功率的增加呈现线性下降的趋势. 干扰距离中心频率f0越近，失锁时的信噪比值越高. 同频和临频干扰时，误码率随干扰信号功率增加而上升，直到链路中断，同频干扰失锁时的误码率低于临频干扰. 相比同频和临频干扰，当干扰信号位于接收机通频带边缘，失锁时的误码率较低.

③ 对数据链施加双频连续波干扰时，与单频干扰效应相似，信噪比先随着干扰功率的增加而线性下降，直到距失锁阈值1 dB处时信噪比显著降低，呈现出非线性变化趋势. 双频干扰导致数据链失锁时的信噪比低于只施加其频率组合中某一单频干扰的信噪比. 在误码率方面，在某一频率固定的情况下，另一频率的频偏越大，总体误码率水平越低，误码率随干扰的上升越快. 数据链对含有临频干扰的双频干扰组合较为敏感，在较低的干扰强度下就能获得较高的误码率.