面向医疗数据安全存储的增强混合加密方法

康海燕， 邓婕

(1.北京信息科技大学 信息管理学院，北京 100192；2.北京信息科技大学 计算机学院，北京 100101)

新冠肺炎疫情期间，医疗机构作为“抗疫”的最前线，在网络空间的战场上同样面临着严峻的数据隐私安全威胁与考验. 亚信安全威胁情报中心在此期间对医疗行业网络安全进行了紧密的监控. 数据显示，疫情期间的绝大多数医疗数据泄露事件是恶意用户利用新型冠状病毒的热度，通过钓鱼软件、恶意链接等方式诱导被攻击用户打开、下载并启用恶意文件来窃取医疗数据. 而一旦电脑被感染，病毒会进行横向移动，感染更多网络中的机器. 据盛邦安全监测数据显示，2020年初以来，部分疫情灾区的WebShell日攻击流量达到104万条，其中有效攻击量近6 000条，相比较2019年的平均日攻击流量上升5个百分点，有效攻击数量上升15个百分点[1]. 此外，2020年1月，美国Verizon电信公司发布了美国《2019年全年数据泄露事故调查报告》，该报告指出医疗保健行业发生的数据泄露事故在所有行业事故中排第二，约占21%；有人专门做过统计，仅2019年美国就发生40多起严重医疗数据泄露事件[2]，大约近千万病人的信息被窃取，同样的在我国，医疗信息泄露事件也是层出不穷，例如2019年9月，我国多家著名医疗机构的影像归档和通信系统服务器被黑，将近30万病人隐私信息被窃取[3]. 近十年来，我国医疗信息泄露事件是屡见不鲜，有统计表明，我国在2010—2019期间因医疗信息泄露事件造成的损失达近万亿，被泄露的公民隐私信息近10亿条. 究其根本原因还是医疗信息系统的防御能力差，存在业务逻辑漏洞，无法安全存储病人的隐私数据，使得恶意用户可以很轻易地进行入侵并窃取数据. 2010—2019年期间我国医疗数据泄露的来源趋势图如图1所示[3]，可以看出除了内部人员窃取或丢失数据等内因外，更多的是来自外部的黑客渗透入侵、未经授权访问或接口暴露等网络攻击威胁.

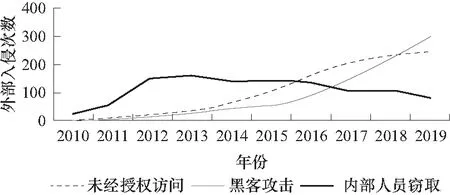
图1 2010—2019年我国医疗数据泄露的来源趋势图Fig.1 Source trend of medical data leakage in China from 2010 to 2019

数据加密技术被誉为信息安全的核心技术，其主要分为对称加密和非对称加密，分别以DES算法(data encryption standard, DES)[4]和RSA算法(Rivest-Shamir-Adleman, RSA)[5]为典型代表. DES算法是分组加密算法，计算效率高、加密速度快，不过其安全性依赖于密钥，而RSA算法是基于大数分解的算法，采用公钥和私钥的双密钥体制，其破解难度等同于分解两个大质数之积，安全性高，不过计算开销大、加密速度慢. 虽说目前还没有在短时间内破译它们的有效方法，但是随着计算机软硬件的不断发展使得计算机的性能日新月异，一些传统的数据加密算法在实际应用过程中已被证实(如DES、RSA和MD5等)容易被破解[6-7]，并且由于采用传统的基于数论的加密算法对数据完全加密不能满足大数据量和实时性(如医疗数据存储)等要求. 因此本文为了更好地解决医疗信息系统中数据安全存储的问题，首先针对DES存在的优点和不足进行分析，并结合三重DES加密算法(triple data encryption algorithm, Tri-TDEA)以及独立子密钥DES加密算法(independent sub key DES algorithm, ISK-DES)的优点，提出改进的双重DES加密算法(improved Bi-DES encryption algorithm based on Tri-DES and ISK-DES,IBDES)；然后对影响RSA算法模幂运算速度的判断质数方法进行详细研究，在不影响RSA安全性的基础上，对原有的质数判断方法进行了改进，提出增强质数判断的RSA算法(RSA algorithm based on enhanced prime number decision,EPNRSA)，最后形成基于IBDES和EPNRSA的医疗数据混合加密方法，使其能有效地对医疗数据进行安全的存储.

1 医疗数据的增强混合加密方法设计

1.1 改进的双重DES加密算法(IBDES)

1.1.1DES算法的概述

DES是由IBM在1972年开发的对称加密算法，也称为数据加密标准，它在国际上广泛使用. DES是一种块加密算法，它使用64位数据块块加密机制处理二进制数据. 数据包长度和密文包长度均为64位(8字节)，并且没有数据扩展名. 密钥长度也是64位，其中56位是有效密钥长度. 其余的8位是奇偶校验位. DES的体系都是公开的，系统的安全性取决于密钥的机密性.

DES的不足之处：(1)存在弱密钥. DES中有12个半弱密钥和4个弱密钥. 因为在生成子密钥的过程中将密钥分为两部分，所以若将这两部分分为全0或全1，则在每一轮中生成的子密钥都是一样的. 当密钥全部为0或全部为1时，或者为1或0各半时，将生成弱密钥或半弱密钥，这将降低DES的安全性. (2)密钥长度过短. DES的加密单元仅为64位二进制，并且有8位是应用于奇偶校验或其他通信开销，所以有效密钥只有56位. 因此这将不可避免地降低DES的安全性. (3)数据传输速率小，不适合做长久数据保护，并且容易受到差分密钥的破解. 由于DES这些明显的不足，美国国家标准与技术研究院在1997年不再对DES进行研究，而是研究其替代方法，即高级加密标准[8](advancde encryption standard,AES).

1.1.2DES的最新研究分析

国内外学者进行了许多尝试来改善DES算法，相继提出了更具影响力的三重DES算法[9](Tri-DES)和独立子密钥DES算法[10](ISK-DES).

1) 三重DES算法.由于传统的DES算法密钥长度短且容易被破解，因此，研究人员提出了一种三重DES加密算法(Tri-DES)，即让DES的密钥长度增加了3倍，并且3个不同的密钥用于三重加密和解密. 加密过程是：首先用第一重密钥k1加密，然后用第二重密钥k2解密，最后用第三重密钥k3再次加密，即C=Ek3(DK2(Ek1M)). 而解密则是逆序，即M=Dk1(EK2(Dk3C)). Tri-DES的核心就是利用k1、k2、k3对明文执行多次加密，密钥长度为DES的3倍. Tri-DES算法具体实现过程如图2所示.

图2 Tri-DES加解密过程Fig.2 Tri-DES encryption and decryption process

此方法虽然增加了密钥的长度，提高了算法的安全强度，有效避免了暴力破解，但是其计算时间却增加了n-1倍，因此运行效率很低. 此外，尽管Tri-DES中的关键位数为168位，但对于当前的计算机算力而言，还是无法避免暴力破解的威胁.

2) 独立子密钥的DES算法. ISK-DES算法的关键取决于采用不同的随机生成的子密钥进行加密，也就是说，每次迭代中的子密钥不用相同的56位二进制密钥生成. 由于16个迭代中的每轮都用48位密钥，所以ISK-DES修改后的DES密钥长度变成了768位. 这种方法可以大大增加穷举解密的难度，从而提高了DES的加密强度，但是密钥长度过长，开销也变大.

1.1.3改进的双重DES加密算法(IBDES)设计与分析

本文在Tri-DES算法和ISK-DES算法的基础上，提出改进的双重DES加密算法(improved Bi-DES encryption algorithm based on Tri-DES and ISK-DES ,IBDES)， 该算法的核心思想为增加密钥长度，并根据随机生成的映射随机数(1～128)，随机生成两个子密钥(双随机性)，然后进行加密，具体过程详见：改进算法A. 解密过程：输入密文，先用key2解密一次后再用key1进行第二次解密还原成明文M.

改进算法A：

输入：明文M，随机生成的128位key映射表

输出：密文C

① 密钥长度处理：将原DES的64位密钥进行扩充，变为128位长度.

② 双随机的子密钥处理：根据随机生成的映射表(表1)随机得到两个子密钥key1和key2，两个子密钥均为64位；进一步处理分别得到16个子密钥.

③ 加密：输入明文，进行双重加密. 先用key1加密一次，再用key2进行二次加密生成密文C.

④ 输出：密文C.

IBDES算法分析：该算法的映射表和子密钥都是随机生成的，体现了一种双随机性，在时间复杂度不变的情况下增加了破解难度.

1.1.4IBDES算法的实验与分析

为了证明本文提出的IBDES算法加密效果的有效性，将IBDES算法与三重DES算法(Tri-DES)和独立子密钥DES算法(ISK-DES)进行实验比较.

(1)测试环境. 硬件：8G内存、Intel i5处理器. 软件：32位Windows 10操作系统、Microsoft Visual Studio 2010、MySQL5.0，eclipse2018，Tomcat8.0. 测试时间工具：eclipse自带System.currentTimeMillis();//获取系统时间函数.

(2)测试用例. 测试用例为纯文本，单位为kB，具体如图3所示.

图3 加密测试文本Fig.3 Encrypted test text

(3) 测试方法. 用Tri-DES、ISK-DES和IBDES算法，加密同样的文本的加密效果和执行加密时CPU消耗时间来进行比较. 表1给出了3种算法的加密文本的执行CPU时间对比，实验共3组，每组运行30次，加密时间取平均值.

表1 3种改进的DES算法的加密文本的执行时间对比

实验分析：从表1可以看出IBDES相比于Tri-DES在加密效率上有明显的优势，并且和ISK-DES算法加密效率几乎持平. 这是因为IBDES算法集结了Tri-DES和ISK-DES两者的优点，IBDES首先将原64位密钥扩展至128位，减少了密钥过短被穷举攻击的风险，然后借鉴Tri-DES算法多重加密的优点，对加密信息进行双重加密，加强了算法的安全强度，最后参考ISK-DES算法的特点将16位密钥进行映射，实现了局部独立性，避免密钥被暴力破解的威胁，两者相辅相成，并且由于只有双重加密，运行效率方面要比Tri-DES算法要高.

以“IBDES算法原理及改进.txt”文本为例，执行DES和IBDES加密后的内容如图4所示.

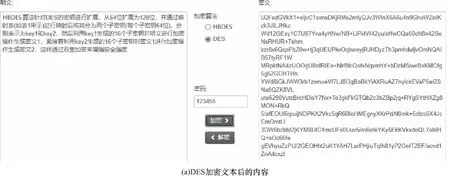
图4 DES和IBDES加密文本内容的效果对比Fig.4 Effect comparison of DES and IBDES encrypted text content

续图4 DES和IBDES加密文本内容的效果对比Fig.4 Effect comparison of DES and IBDES encrypted text content

从图4可以看出DES加密本文后内容只有数字〗大小写字母的组合，IBDES算法的加密后内容除了数(〗字+大小写字母的组合之外还有@∧_等一些特殊字符，比DES加密的效果要更复杂，因此IBDES算法要比DES加密效果要更好.

1.2 增强质数判断的RSA算法(FPNRSA)

1.2.1RSA的概述

RSA算法由RonRivest、AdiShamir和LeonardAdleman[5]三人在1977年合作提出并于1987年首次公开，是非对称的加密算法. 其中很重要的一点是用来加密数据的密钥并不需要和数据一起传送，因此这就减少了密钥泄露的可能性. RSA被认为是非常安全的，但它的计算速度比DES要慢很多. 同DES一样，PSA算法的安全性从没被证明过，但想攻破RSA算法涉及大数的因式分解(包含至少200位的大数)，而这是一个极其困难的问题(就算有计算机帮助也几乎不可能)[11-13]. 由于缺乏解决大数的因式分解问题的有效方法，因此可以推测出目前没有有效的方法可以破解RSA. 因此，RSA是目前最重要的加密算法之一，它可以抵抗迄今为止已知的大多数密钥攻击，而且ISO将其作为公钥数据加密标准.

RSA的不足之处：(1)难实现一次一密. 由于密钥产生繁琐，必须采用两个大质数p、q来产生RSA的密钥，所以局限于质数生成技术，几乎很难一次一密. (2)加密速度慢. RSA算法不仅具有DES没有的高安全性，而且加密速度慢. 此外，RSA的p、q等大质数都是使用确定性质数判断算法随机产生的，所以RSA与DES的加密时间几乎相差百倍.

1.2.2RSA的最新研究分析

RSA算法的安全性是基于大数分解的算法，由于大数分解是公认的数学难题，所以RSA的安全性很高. 尽管现在计算机硬件的更新迅速，让计算机的性能不断突破极限，但是对大数分解仍需要大量时间才能破解. 此外，RSA算法为了应付计算机算力的高速发展，逐渐增加密钥的长度，但是RSA算法加密速度恰恰是被 密钥的生成速度所限制. 为了解决RSA算法加密速度问题，国内外研究人员普遍采用两种方法.

第一种方法是寻找替代RSA的新的公钥加密算法，例如基于椭圆曲线[14](ECC)的公钥加密算法，ECC的问世实现了效率上的重大突破，不过因尚未得到广泛使用，所以目前大量研究仍是基于理论上的. 第二种方法是改进密钥算法的实现[15-18]，并采取某些措施来加快其运算速度，本文也是从这一方面着手，研究如何改进RSA密钥的生成，改善其运算速度. 由于RSA的核心算法是运算大质数的模幂运算，即大数自乘取模，所以要提高RSA算法的效率，就必须要解决RSA中模幂运算的速度问题，而模幂运算中核心复杂度取决于取模操作，取模操作又包含除法运算，对于计算机而言，进行一次除法运算需要进行数次加减移位运算，这是相当耗时的，所以假设能让RSA算法极力降低取模操作甚至避免取模操作，则RSA算法的性能会得到显著的提升.

1.2.3增强质数判断的RS算法(EPNRSA)的设计与分析

在以上分析基础上，提出了增强质数判断的RSA算法(RSA algorithm based on enhanced prime number decision,EPNRSA). 其核心思想：采用Montgomery快速幂算法[19]对经典的概率性质数判断算法—Solovay-Strassen算法进行优化，设计了增强质数判断算法(enhanced prime number judgment algorithm,EPNJA)，再将EPNJA应用于RSA算法，形成增强质数判断的RSA算法(EPNRSA). 其核心技术如下.

(1) 质数的判断方法. 质数的判断方法整体上分为两类：一是确定性质数判断算法，二是概率性质数判断算法. 确定性数判断算法意如其名，就是通过它生成的数就百分百是质数，不过却带有一定的限制. 而概率性判断算法虽然无法保证百分百生成质数，却没有什么大的限制且生成质数的速度也比确定性判断算法快. 总的来说，实际生活中大多是采用概率性质数判断算法，虽不能保证百分百生成质数，但是生成非质数毕竟是小概率事件，而且概率性质数判断算法可以快速且不规则地生成伪素数，满足大多数需求.

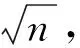
② 概率性质数判断算法. 其中较著名的算法有：Miller-Rabin算法[20]、Solovay-Strassen算法[21]、Lehman算法[22]等，由于本文针对Solovay-Strassen概率性质数判断算法进行改进且限于篇幅，所以仅对Solovay-Strassen算法进行详细介绍. 令0≤a≤n，随机选取a，计算雅可比函数J(a,n). 若n为素数，则GCD(n,a)=1,且J(a,n)=2(n-1)/2modx. 若n不为素数，则至多有1/2的概率使上式成立. 若n通过了t次检验，则n不是素数的概率将为2-t.

(2) 增强质数判断算法. 引入可以极大减少模幂运算的Montgomery快速幂算法对Solovay-Srtassen算法进行优化，提出一种增强质数判断算法(EPNJA). 该算法的核心步骤为选择一个与模数N互质的正整数R作为基数，同时要求当R为2k时N需满足2k-1≤N≤2k并且要求GCD(R,N)=1，然后利用Montgomery幂算法大数A、B进行模乘运算，即Montgomery(A,B,N)=ABR-1(modN)，最后输出大数A、B的模乘结果.

(3) 增强质数判断的RSA算法(EPNRSA).

为了提高EPNJA应用于RSA算法的判断效率，本文在质数生成初始阶段直接剔除所有偶数以及被5整除的数，并通过预处理算法程序寻找1亿(这里可以根据需求来寻找更大范围内的卡迈克尔数[23])以内的255个卡迈克尔数形成卡迈克尔特殊合数表对特殊的合数进行质数判断的RSA算法(EPNRSA)，具体过程详见：改进算法B. 解密过程：输入密文C，用两个大质数生成RSA密钥对密文进行解密生成明文M.

EPNRS算法分析：增强质数判断算法EPNJA采用Montgomery快速幂算法对Solovay-Strassen算法进行优化的主要优势是将除法化为移位运算，提高了大数幂乘运算的效率，应用于RSA后可以进行质数的快速筛选，简化了计算过程，可以有效抵抗对RSA算法的强制破解.

改进算法B：

输入：明文M，卡迈克尔特殊合数表CN，随机大数组N，Solovay-Strassen算法；

输出：密文C.

① 随机大数生成：随机生成一组除了偶数以及能被5整除的数之外的大数组N.

② 大数组筛选：通过卡迈克尔特殊合数表CN对大数组N进行筛选.

③ 优化Solovay-Strassen算法：利用Montgomery快速幂算法优化Solovay-Strassen算法.

④ 大质数p、q生成：结合步骤1、2、3以及EPNJA来生成两个大质数p、q.

⑤ RSA加密明文：输入明文M，用两个大质数p、q生成RSA密钥对明文进行加密生成密文C.

⑥ 输入密文C.

1.2.4EPNRSA算法的实验与分析

本文将提出的EPNJA判断算法与Miller-Rabin、Solovay-Strassen和Lehman三种著名的判断算法进行判断质数比较，实验数据范围选取[0,1 000]，它们判断的次数和所用时间的关系如表2所示.

表2 各概率性质数判断算法在不同判断次数上所消耗的时间对比Tab.2 Comparison of time consumed by esch probabilistic prime number judgment algorithm in different judgment times

从表2可以看出，EPNJA判断质数的概率不仅比其他3种算法要高，而且生成质数的时间也大大缩短了. 将改进的质数判断算法应用到RSA加密算法中形成增强质数判断的RSA算法(EPNRSA)，并与RSA算法进行加密耗时对比，运行结果如图5所示.

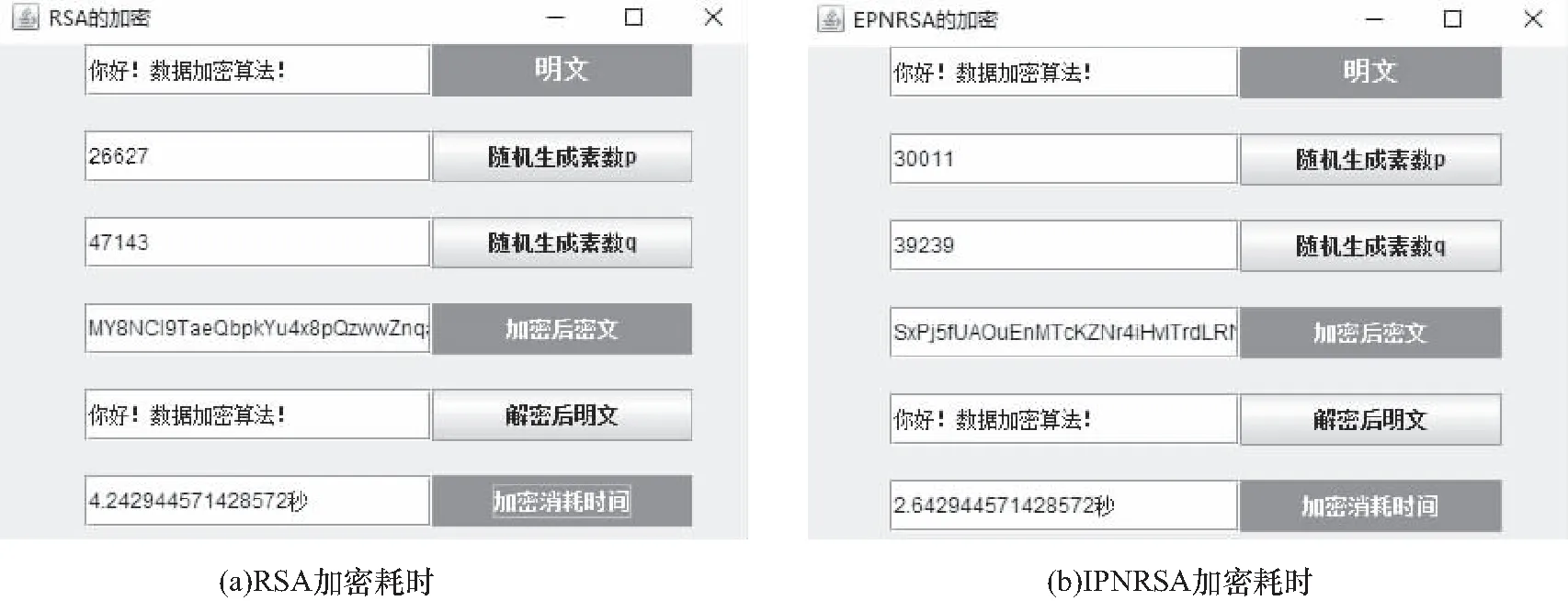
图5 RSA算法和EPNRSA算法的加密时间对比Fig.5 Consuming time of encryption between RSA algorithm and EPNRSA algorithm

从图5中加密消耗时间可以明显看出，生产相同位数的p、q时，EPNRSA花费的时间要比RSA少.

1.3 医疗数据的增强混合加密方法的设计与分析

为解决医疗电子病历数据加密效率低和加密安全性不高问题，融合对称加密算法(DES→IBDES)和非对称加密算法(RSA→EPNRSA)二者的优点，提出基于IBDES和EPNRSA的医疗数据增强混合加密方法，如图6所示. 具体流程如下.

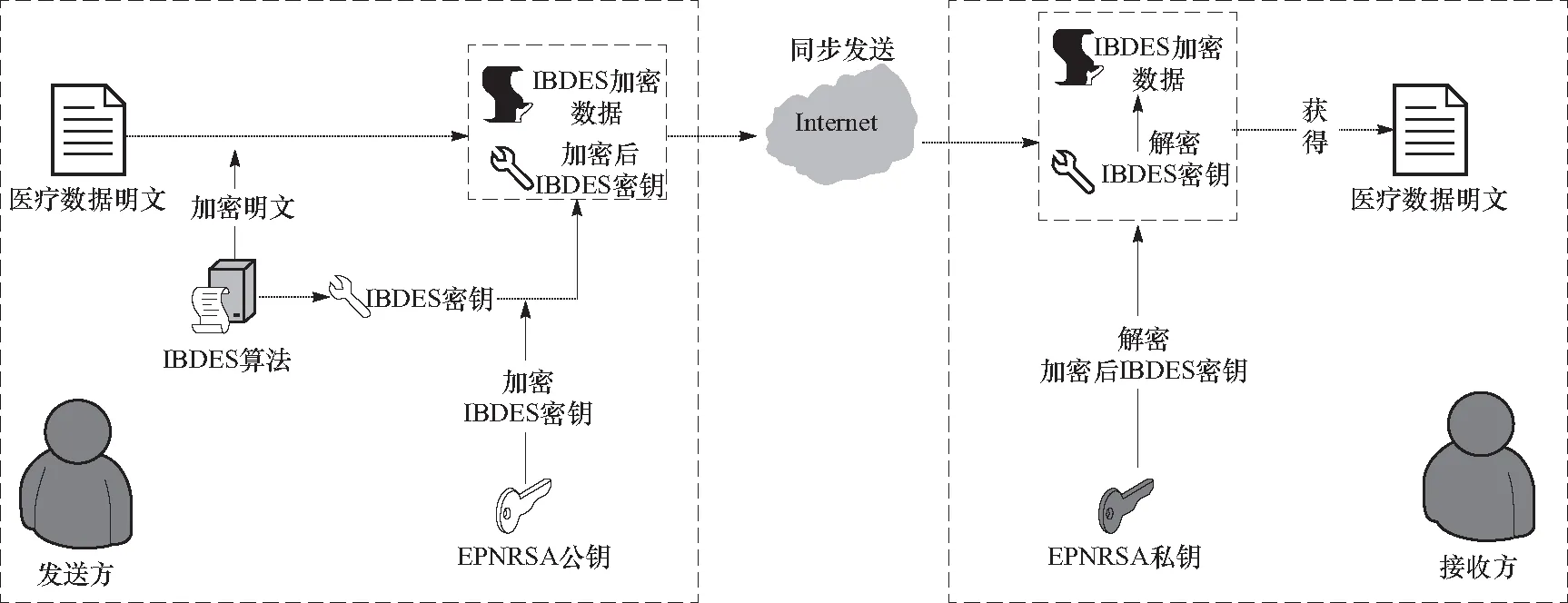
图6 基于IBDES和EPNRSA的医疗数据增强混合加密方法Fig.6 Enhanced hybrid encryption method for medical data based on IBDES and EPNRSA

① 发送方申请获取医疗数据，授权通过后，用IBDES密钥对医疗数据明文加密，得到密文.

② 发送方用EPNRSA的公钥去加密IBDES密钥信息，得到加密后的公钥，并将加密的密文和加密后的公钥混合信息同步发送出去.

③ 接收方收到混合信息后，使用EPNRSA的私钥解密加密后的公钥，得到IBDES密钥，再用IBDES密钥对加密的密文进行解密得到医疗数据明文.

1) 安全性分析.

IBDES算法的映射表和子密钥都是随机生成的，体现了一种双随机性，在时间复杂不变的情况下增加了破解难度. EPNJA算法采用Montgomery快速幂算法，将除法化为移位运算，提高了大数幂乘运算的效率，应用于RSA算法后形成EPNRSA算法可以进行质数的快速筛选，简化了计算过程. 故基于IBDES和EPNRSA的增强混合加密方法不仅提升了加密医疗数据EMR的效率，更是保证了传输医疗数据EMR的安全性.

2) 时间复杂度分析.

基于IBDES和EPNRSA的医疗数据增强混合加密方法是分步的，其中第①步用IBDES密钥进行数据加密，假设数据字符个数为n，那么一次DES加密的时间复杂度为O(n)，IBDES是两次独立加密所以时间复杂度为2O(n)，第②步中再用EPNRSA的公钥加密IBDES密钥信息得到加密密钥，因为EPNRSA是基于RSA算法的，RSA算法时间复杂度都基本耗费在寻找大素数生产密钥过程，即RSA的生成密钥时间复杂度为O(log(pq))O((log2p+log2q)，但是本文的EPNRSA改良了RSA的素数生成速度，即预处理和利用Montgomery快速幂算法优化Solovay-Strassen算法，省去了大数乘法O(logp+logq)=O(logpq)，所以时间复杂度为O(log2p+log2q)，第③步中发送方将加密密文和加密密钥混合信息发送出去的时间是传输时间，不计入方案的加解密时间，并且解密是第①步和第②步相反的步骤，因此时间复杂度一样为2O(n)和O((log2p+log2q)，最后得出基于IBDES和EPNRSA的医疗数据增强混合加密方法的时间复杂度为4O(n)+2O(log2p+log2q).

1.4 医疗数据增强混合加密方法的验证与分析

为了验证本文提出的基于HBDES和IPNRSA的医疗数据增强混合加密方案的有效性，将其与传统的基于DES和RSA的混合加密方案分别从算法加密时间效率和算法加解密性能效率两方面进行详细的实验对比和结果分析.

1.4.1时间效率分析

对基于DES和RSA的混合加密方法和基于IBDES和EPNRSA的医疗数据增强混合加密方法进行密钥长度和生成速度的比较分析如下：IBDES算法是把DES的56位密钥进行了扩展，即从56位变为128位，不过只扩展了1倍长度密钥，所以对于扩展后密钥的产生速度几乎没有影响. 此外，这里RSA加密算法选用了1 024 bit的密钥，而EPNRSA加密算法，因为采用了增强质数判断算法(EPNJA)来产生密钥，所以密钥生成速度明显快于RSA。表3给出了两种加密算法在单独运行时，对少量医疗数据量信息(200 bit)加密所花费时间对比，共8组实验，每组运行30次，加密时间取平均值.

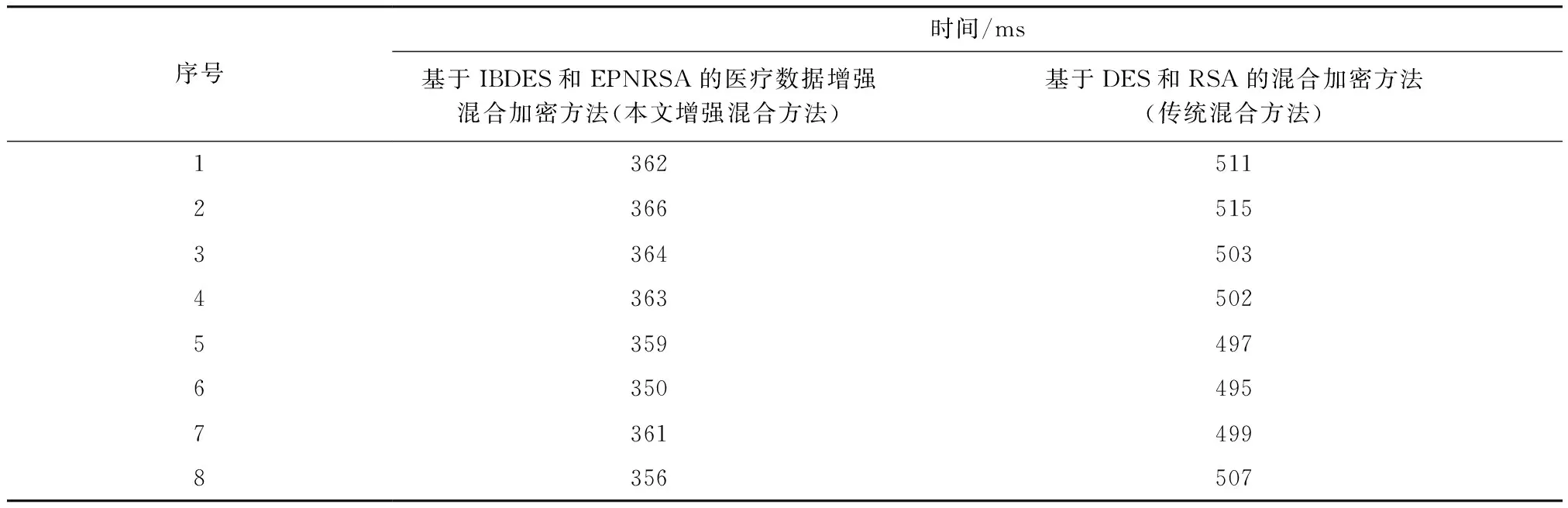
表3 两种加密方法的加密少量数据的时间比较Tab.3 Time comparison of two encryption schemes for encrypting a small amount of data

实验分析：从表3中可知，在加密一次短消息时，这两种加密方案之间的时间差保持在150 ms左右的水平. 人类几乎无法感知这种细微的时间差距，但是随着密次数增大时，则耗时的差距会变得相当可观。举个例子，某网页用户采用静态数据加密方式，每次加密后的结果都是一样的，即不采用一次一密的方式，即使采用公钥加密体制的RSA算法其结果也一样，所以只要有恶意用户拦截加密的消息，并以此模拟表单提交信息，就可以骗过加密系统直接入侵，显然这样静态加密方式是不可取. 因此，采用一次一密的方式，才能避免这种风险. 此外，如果是对较大数据量医疗信息(超过2 M)加密时，这两种加密方法的加密时间会将是百倍以上的差距. 所以基于IBDES和EPNRSA的医疗数据增强混合加密方案的加密效率要比传统的基于DES和RSA的混合加密方案有明显的优势.

1.4.2性能效率分析

本文采用真实的医疗电子病历数据图片进行加解密，实验结果如图7和图8所示，实验分析如下.

1)医疗数据图片明文加密效果明显. 从图7(a)可以看出加密前的医疗数据图片文字部分清晰可见，然后执行加密操作后得出医疗数据图片密文(见图7(b))，从图7(b)中可以看出，几乎所有文字部分都无法识别，后台再执行查看源文件操作时都以乱码的形式表现出来，这充分表明本文提出的医疗数据增强混合加密方法的加密有效性.

图7 医疗电子病历数据的加密前后对比Fig.7 Comparison of medical electronic medical record data before and after encryption

2)医疗数据图片密文解密效果明显. 从图8(a)可以看出解密前的医疗数据图片整张模糊不清几乎不可识别，然后执行解密操作后得出医疗数据图片密文(见图8(b))，与图7(a)原图进行对比，明显看出加解密前后图片几乎无损，这充分表明本文提出的混合加密方法的解密有效性.

图8 医疗电子病历数据的加密前后对比Fig.8 Comparison of medical electronic medical record data before and after encryption

2 结 论

目前，医疗信息、电子病历和其他医疗系统已成为现实生活中必不可少的部分，并且它们的安全性也引起了越来越多的重视. 特别是在新冠疫情期间，人们无时不刻不在关注自身的健康信息和医疗数据的安全. 为了更好地解决医疗信息系统中数据安全存储的问题，在传统的DES和RSA算法的基础上提出了基于IBDES和EPNRSA的医疗数据增强混合加密方法. 通过对传统的基于DES和RSA的混合加密方案在加密时间效率和算法加解密性能效率两方面进行详细的实验对比，可以发现该方案在各个方面都能很好地保障医疗数据的隐私安全. 本文的主要创新之处包括以下几个方面.

① 设计了改进的双重DES加密算法(IBDES)：该算法借鉴三重DES加密算法(Tri-DES)和独立子密钥DES算法(ISK-DES)的优点，把DES的密钥从64位扩展为128位，并通过(双随机性)随机生成128位的映射表进行映射后将其随机分为两个子密钥key1和key2(每个子密钥64位)，然后利用key1生成的16个子密钥对明文进行加密操作生成密文1，紧接着利用key2生成的16个子密钥对密文1进行加密操作生成密文2，这样通过双随机性双重加密来增强安全强度，相比传统的DES算法的加密安全性有了大大提升且加密效率并没有降低.

② 构建了增强质数判断的RSA算法(EPNRSA)：该算法针对影响传统RSA算法的加解密效率的核心步骤——大质数的模幂运算进行改进，摒弃传统的模幂运算，采用Montgomery快速幂算法对Solovay-Strassen算法进行优化，取消了RSA计算过程中取模操作和降低了RSA的计算量，不仅大大降低RSA的加密时间复杂度，同时加密安全质量并没有受到影响.

③ 提出基于IBDES和EPNRSA的医疗数据增强混合加密方法：该方案结合了DES、RSA以及它们改进算法的特点，具有加解密效果好、执行速度快以及安全性高等优点. 此外，该方案继承了公钥加密体制的特性，所以不需要担心密钥管理相关问题，是面向医疗数据安全存储的一种理想方案.

未来将会从以下几个方面入手继续研究和完善：①在大量医疗图像信息环境下继续改进文章的数据加密方法使其适用安全、快速压缩加密；②研究不同医疗数据信息下的新数据加密方法；③应用基于IBDES和EPNRSA的医疗数据增强混合加密方法解决医疗数据安全领域的实际问题.