幅度误差对抗干扰性能的影响分析
张新帅,康 博,肖永丽,李 军,沈 磊,丁 可
(1.四川九洲电器集团有限责任公司,四川 绵阳 621000;2.四川九洲北斗导航与位置服务有限公司,四川 绵阳 621000)
0 引 言
随着北三组网,我国北斗卫星导航系统已在各行各业得到广泛的应用,已成为不可或缺的一部分。由于接收到的卫星信号功率远低于环境噪声,容易受到干扰信号的影响,因此部分领域的导航设备需要加装阵列天线进行抗干扰处理。由于阵列天线的各个阵元方向图不可能完全相同,可能会存在较大的幅度误差,不少文章认为幅度误差会造成干扰零陷深度的大幅变浅,从而影响抗干扰性能[1-2]。当前主流的抗干扰技术为空时抗干扰技术和空频抗干扰技术[3-4],二者抗干扰性能基本相同。本文基于空时抗干扰技术,对幅度误差引起的抗干扰性能进行了仿真分析,结果表明幅度误差会使零陷深度急剧变浅,这是由于遍历过程中使用了各个方向的理想导向矢量导致,通过使用阵列天线各个方向的实际导向矢量,零陷深度与无幅度误差时基本无变化,输出信干噪比也基本相同。
1 空时抗干扰技术
空时抗干扰技术是在纯空域抗干扰技术的基础上,在其阵元后面增加若干个时间延迟形成空时二维处理结构[5],其结构如图1所示。

图1 空时抗干扰滤波结构图
设有M个阵元,N个时间延迟单元。每个时间延迟单元的时延为τ,要求τ≤1/B,其中B为处理带宽。用MN×1维的X表示接收数据向量:
X=[x11,x12,…,x1N,x21,x22,…,x2N,…,xMN]T
(1)
式中:xmn表示第m个阵元第n个抽头所接收到的信号。
用MN×1维的W表示权矢量:
W=[w11,w12,…,w1N,w21,w22,…,w2N,…,wMN]T
(2)
式中:wmn表示第m个阵元第n个抽头的权系数。
最优权矢量可表示为:
Wopt=(SHR-1S)-1R-1S
(3)
式中:R=E(XXH),为接收数据的协方差矩阵;S为空时二维导向矢量,本文采用功率倒置算法,空时导向矢量S为MN×1维,S=[1,0,0…]T。
得到的最终输出为:
y=WoptHX
(4)
在俯仰角i,方位角j方向上的增益可表示为:
(5)
式中:sij表示为阵列天线在俯仰角i,方位角j方向上的导向矢量。
2 导向矢量修正
无幅度误差时阵列天线接收到的数据X可以表示为:
(6)
式中:ki表示第i颗卫星信号;Ai表示第i颗卫星信号对应的导向矢量;p表示卫星信号的个数;gj表示第j个干扰信号;Bj表示第j个干扰信号对应的导向矢量;q表示干扰信号的总个数。
(7)

最优权矢量可表示为:
(8)
最终输出可表示为:
(9)
在俯仰角i,方位角j方向上的增益可表示为:
(10)
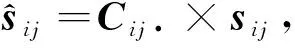
3 仿真试验
3.1 无幅度误差抗干扰性能仿真
仿真条件:7阵元均匀圆阵,阵元间距95 mm,卫星信号信噪比为-25 dB,入射方向俯仰角30°,方位角150°,1个干扰信号干信比为100 dB,入射方向俯仰角60°,方位角40°,无幅度误差的零陷图、输出频谱图、100次仿真的输出信干噪比统计图如图2~图4所示。

图2 无幅度误差零陷图
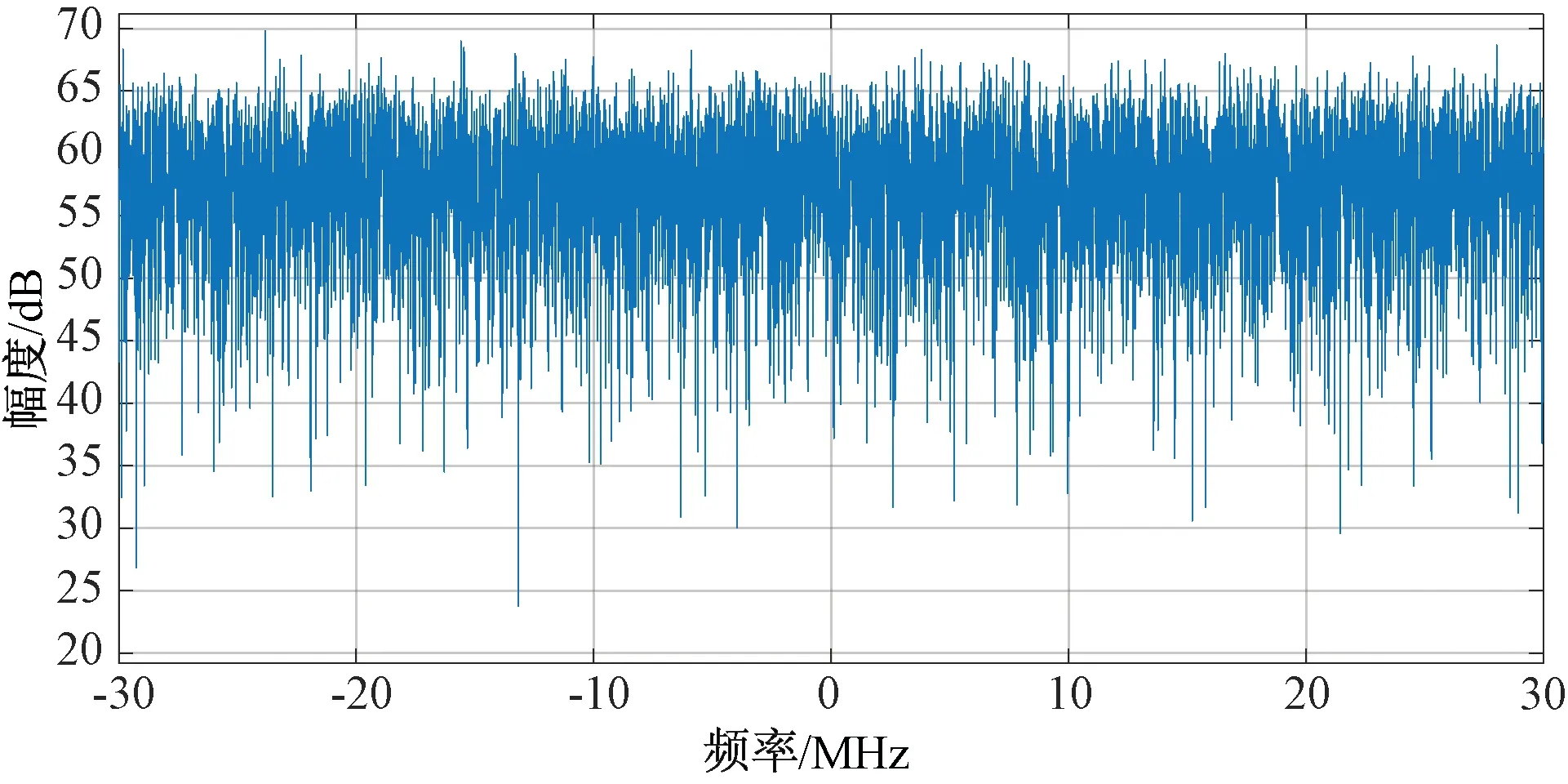
图3 无幅度误差输出频谱图

图4 100次信干噪比输出统计图
从图2~图4可以看出,无幅度误差的情况下,在干扰信号入射方向俯仰角60°、方位角40°上形成了105.8 dB深度的零陷,将干扰信号抑制在环境噪声以下,平均输出信干噪比为-27.3 dB,有效地滤除了干扰信号对卫星信号的影响。
3.2 有幅度误差抗干扰性能仿真
仿真条件1:采用7阵元仿真方向图,四周阵元与中心参考阵元的最大幅度误差为5.9 dB,其它仿真条件与3.1相同,采用理想导向矢量sij进行遍历的有幅度误差零陷图、输出频谱图、100次仿真的输出信干噪比图如图5~图7所示。

图5 有幅度误差零陷图

图6 有幅度误差输出频谱图
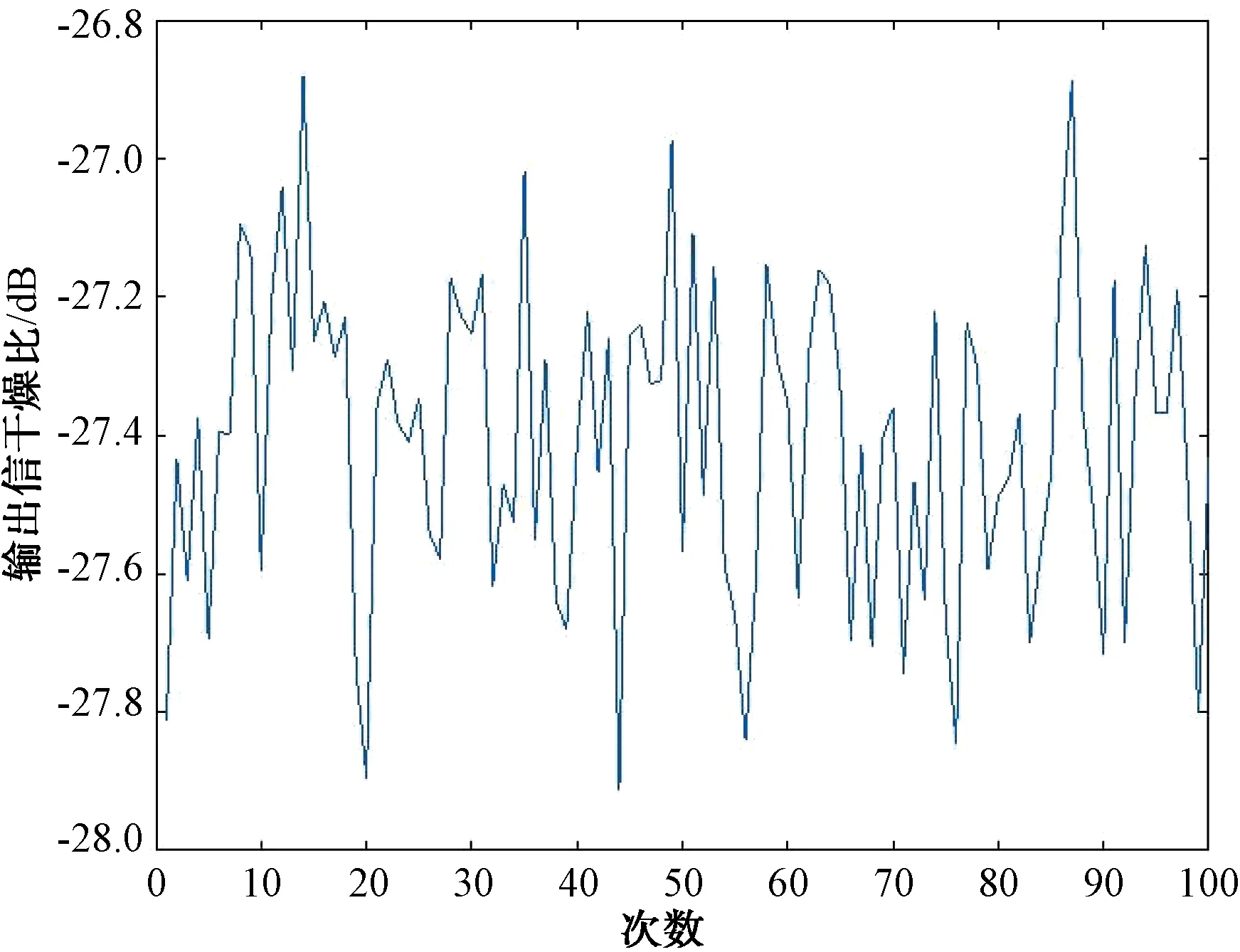
图7 100次信干噪比输出统计图
从图5可知,使用理想导向矢量sij进行遍历,在干扰方向上零陷增宽且急剧变浅,只有-14.92 dB,但通过图6和图7可知,输出信号频谱和输出信干噪比(平均-27.4 dB)与无幅度误差时的仿真结果基本相同,因此可以判定此时干扰已被滤除,是使用理想导向矢量sij进行遍历得到的零陷图出错。
4 结束语
本文从空时抗干扰技术出发,给出了当存在幅度误差时,对遍历各个方向上形成的增益所应使用的导向矢量。通过无幅度误差和有幅度误差时对抗干扰性能的仿真分析,证明了幅度误差不会使得干扰零陷深度急剧变浅,输出信干噪比也基本相同。

