基于色散介质与光纤光栅的宽带微波光子频率测量性能研究

郝 汀，陈 捷，赵明峰

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

现代电子战中，电磁环境越来越复杂，如何在复杂的电磁环境中快速获取敌方雷达信号的参数信息(包括频率信息、幅度信息、脉宽信息等)成为电子战的重要部分。其中，微波信号的频率信息是众多参数信息中最为基本的信息，也是获取分析其他信息的基础。目前，随着毫米波雷达的不断应用，现代电子战的电磁环境已经有了很多范围在18～40 GHz的射频信号。

传统微波信号的频率测量方法主要是基于电子器件实现的，然而针对毫米波段的信号频率测量，传统的测量方法受限于其电学的模数转换器(ADC)芯片的模拟输入频率范围、带宽等参数，无法直接对毫米波段的射频信号频率进行直接测量，需要将模拟的毫米波信号与参考频率信号进行混频，将毫米波段信号转化到其ADC能够直接测量的频段范围之内。因此，针对宽带毫米波信号的频率测量，传统测频方法结构复杂，功耗大，成本昂贵。随着微波光子技术的发展，利用微波光子技术实现宽带雷达信号频率的测量已经成为了研究的热点[1-8]。

目前基于微波光子技术的宽带测频方法主要包括频率-功率映射方法、频率-时间映射方法、四波混频方法等[9-15]。这些方法各有优缺点，频率-时间法测频精度低，成本昂贵；四波混频法有时无法实现实时测量；频率-功率映射法系统结构较简单，但工程化实现较为困难。本文研究了基于色散介质与光纤光栅结构的微波光子测频方法，并通过仿真分析了光载波波长、色散介质长度以及色散系数等对测频的影响。

1 基于色散介质与光纤光栅结构的微波光子宽带测频原理

1.1 基于色散介质与光纤光栅的测频系统架构

基于色散介质与光纤光栅的测频系统架构如图1所示。该测频系统主要包括激光器、相位调制器、分路器、光纤光栅、色散介质、探测器以及功率数据处理部分等。其主要原理为：激光器输出光载波信号，雷达信号通过相位调制器被调制到光载波上，通过50∶50的分路器将光载波一分为二。其中一路经过光纤光栅和探测器，最终进入到功率数据处理部分；另外一路经过色散介质和探测器，最终与另外一路同时进入到功率数据处理部分。功率数据处理部分将2路通过探测器输出的功率信号进行处理，得到一个雷达信号频率与功率的线性关系，从而实现对雷达信号频率的测量[16-17]。

1.2 基于色散介质与光纤光栅的宽带微波光子频率测量原理

先分析图1中上路,忽略高阶谐波，经过相位调制器输出的双边带信号可以表示[16-17]为：

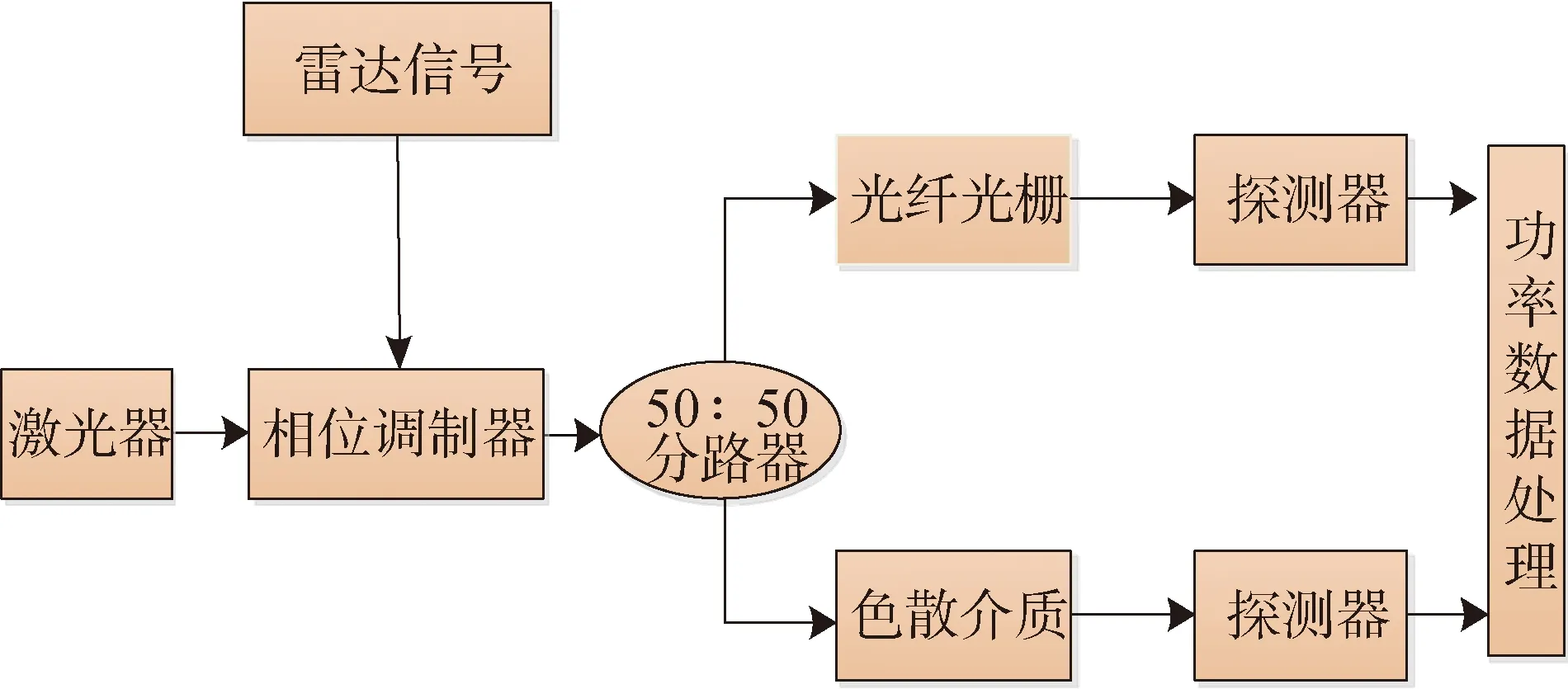
图1 基于色散介质与光纤光栅的宽带微波光子频率测量方法

(1)

通过探测器得到的光电流大小为[16-17]：

i(t)∝|E(t)|2=

(2)

接收到频率为fm的射频信号功率为：

(3)

对于布拉格光纤光栅的光信号，其透射谱的斜边满足以下关系：

P(fm)=P(f0)+αfm=P0+αfm

(4)

式中：P0为光载波的衰减量；α为光纤光栅的透射频率响应特性曲线的斜率。

由式(4)可得到，经过光纤光栅后光载波信号和2个一阶边带的幅度表示为：

A0′=A010P0/20

(5)

A-1′(fm)=A-110(P0-αfm)/20

(6)

A1′(fm)=A110(P0+αfm)/20

(7)

则公式(1)可表示为：

(8)

经过探测器得到的光电流大小[16-17]为：

(9)

由式(9)可知，接收到的频率fm的射频信号的功率可为：

PRF1∝10P0/10[10(P0+αfm)/20-10(P0-αfm)/20]2

(10)

图1中的另一路以单模光纤为色散介质将相位调制转化为强度调制，假设单模光纤的长度为L，由于色散会给光载波信号与2个一阶边带分别产生不同的相位偏移[16-17]。

令ω1=ωc+ωm，相位偏移φ1=βω12L/2，令ω2=ωc-ωm，相位偏移为φ-1=βω22L/2，光载波的相位偏移为φ0=βωc2L/2。

光载波信号经过长度为L的单模光纤传输后的电场为：

EPM2(t)=A0cos(ωct+φ0)+A1cos(ω1t+φ1+

(11)

探测器接收到的光电流为：

(12)

只考虑ωm对应的光电流[16-17]：

(13)

由式(13)可知：

(14)

式中：D为单模光纤的长度；c为光载波速度；λ为光载波波长。

由式(14)可得光探测器接收到角频率ωm的射频信号的功率为：

(15)

在图1中的功率数据处理端，上下2路同时接收到的频率为fm的射频信号功率比可表示为：

(16)

从上式可以看出，光纤光栅的斜率，色散介质的色散系数、长度，激光器输出的光波长均为已知量，功率比只与射频信号的频率有关。当选定好光纤光栅、色散介质以及一定波长的连续光信号就可以通过测量图1中的2路功率比得到射频信号的频率。

2 基于色散介质与光纤光栅的宽带光子测频性能仿真分析

通过OptiSystem软件搭建的仿真链路框图如图2所示。

图2 基于色散介质与光纤光栅的宽带光子测频系统仿真链路

由公式(16)可知，基于色散介质与光纤光栅架构的频率测量主要受到色散介质的色散系数、色散介质长度、光载波波长以及布拉格光栅投射频率相应曲线斜率等影响，为了验证基于色散介质与光纤光栅架构的频率测量性能，本文分别对色散介质系数、长度以及光载波波长等进行仿真研究。

针对色散介质的色散系数，设激光器输出功率为0 dBm，波长为1 550 nm，射频信号从0.5 GHz变化到40 GHz，布拉格光栅的中心波长为1 550 nm，以单模光纤作为色散介质，单模光纤长度为15 km，D分别取17 ps/nm/km、15 ps/nm/km、19 ps/nm/km，得到的仿真结果如图3所示。

图3 不同色散系数下的功率比随频率变化曲线

为了验证色散介质的长度对测频的影响，设激光器输出功率为0 dBm，波长为1 550 nm，射频信号从0.5 GHz变化到40 GHz，布拉格光栅的中心波长为1 550 nm，以单模光纤作为色散介质，色散系数取17 ps/nm/km,单模光纤长度取2 km、5 km、15 km，得到的仿真结果如图4所示。

图4 不同色散介质长度下的功率比随频率变化曲线

为了验证激光器输出光载波波长的变化对测频的影响，设激光器输出功率为0 dBm，波长分别为1 550 nm、1 556 nm、1 550.6 nm,射频信号从0.5 GHz变化到40 GHz，布拉格光栅的中心波长为1 550 nm，以单模光纤作为色散介质，色散系数取17 ps/nm/km,单模光纤长度取2 km，得到的仿真结果如图5所示。

图5 不同光载波波长下的功率比随频率变化曲线

图3、图4和图5的仿真结果表明，选择合适的色散介质系数、色散介质长度以及光载波的波长，基于色散介质与光纤光栅架构的宽带光子测频系统可实现对宽带信号的频率测量。

3 结束语

本文研究了基于色散介质与光纤光栅的宽带微波光子测频系统，首先分析了其测频原理，通过仿真分析了色散介质的长度、色散系数以及光载波波长等对频率测量的影响。仿真结果表明该方法能够实现对宽带毫米波信号的频率测量。本文的研究可为基于色散介质与光纤光栅的宽带光子测频系统的工程化提供支撑。