迭代法求解航天器热网络方程的收敛条件与时间步长优化
耿利寅,韩东阳,张传强,孟恒辉,李国强
(北京空间飞行器总体设计部,北京 100094)
0 引言
热分析计算是航天器热设计验证和在轨温度预示的重要手段。目前,一般航天器热设计中热分析计算的步骤是:建立航天器在轨或试验状态的热物理模型,并将其离散化为一系列描述节点间热交换过程的传热学方程(组),即热网络方程;再通过对热网络方程的求解,获得所关注节点和时段的瞬态温度结果。热网络方程因其中的辐射换热项包含温度的4 次幂而隶属于典型的非线性方程。对于非线性方程,通常采用迭代法进行求解,而目前尚无完善的理论方法能直接判断有限次迭代是否可以获得收敛解。
研究结果表明,对于一个包含辐射换热项的确定的热物理模型,其瞬态计算的收敛性与时间步长密切相关:若设置的时间步长过大,在迭代计算过程中可能引起部分节点温度振荡失稳、不能收敛,造成计算失败;反之则使计算效率低下,耗时过长。因此,对瞬态热计算收敛性与时间步长及其优化选定等开展分析研究,对优化建模、提高计算效率,以及指导模型构建中的合理简化、节点划分和换热关系设定等具有重要意义。
本文对Gauss-Seidel 迭代法求解热网络方程的收敛性问题进行分析,结合航天器热控设计的工程实际,提出一种近似线性化方法,即,将含有辐射项的非线性热网络方程转化为线性热扩散方程。在此基础上进行分析以确定计算收敛的条件和最优时间步长,并辅以算例验证。
1 热网络方程(组)及其节点分类
运行在宇宙空间中的在轨航天器通常无对流换热过程,仅需考虑辐射和传导两种换热方式。对于一个由n
个节点组成的航天器热物理模型,描述其能量平衡的热网络方程为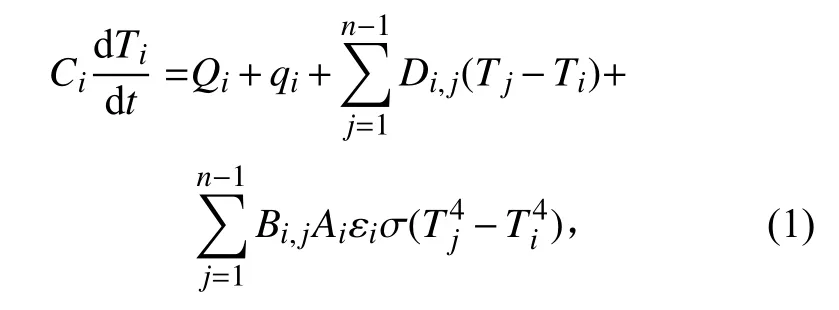
i
,j
代表节点编号,i
,j=
0, 1, …,n
‒1;C
为节点i
的热容,J/K;T
为温度,K;t
为时间,s;Q
为外热流功率,W;q
为内热源功率,W;D
为节点i
、j
间的导热系数,W/K;B
为节点i
、j
间的辐射换热系数(GebHart 系数);A
为节点i
的辐射换热面积,m;ε
为全波长发射率;σ
为Stefan-Boltzman 常量。在实际计算中,通常将一个热分析模型的节点分成3 类——扩散节点、算术节点和边界节点。其中,边界节点温度是已知的,不需求解。扩散节点是具有一定热容,并与其他全部或部分节点有换热关系的节点。在瞬态计算中,给定起始温度,则扩散节点的温度可由式(1)进行迭代计算获得。算术节点通常用以模拟覆盖在实体外的多层隔热组件、薄膜等热容非常小的表面,其热容在模型中设为0,其能量方程与时间无关,实际退化为显式格式,求解不存在收敛性问题。因此,本文主要针对扩散节点开展讨论。
2 求解收敛性与时间步长分析
2.1 方程的线性化近似
考查节点i
在迭代过程中的情况,因研究对象为节点i
,则首先可假设节点i
以外的其他节点都可收敛,并已经收敛,其温度为T
(j≠i
)。对于扩散节点,由于式(1)右侧第4 项的辐射换热项为非线性项,在计算传热学相关领域公开发表的文献中尚未发现其迭代求解收敛性的相关研究结论;但对于线性扩散方程,收敛性研究的结论是明确的。为此,本文考虑首先进行方程的线性化。在迭代法求解方程组的过程中,每个节点的起始温度都是给定的,为了便于分析,将式(1)中的辐射换热项简化为导热形式,即


式(4)与典型的热传导扩散方程形式完全相同,说明通过上述近似转换,已经将式(1)的非线性方程转换为线性方程。需要说明的是,上述线性化近似只用于计算收敛性的分析,实际方程求解时,仍须按照式(1)进行迭代计算。
2.2 节点收敛性分析
在每个特定时间步长的迭代计算中,式(4)中的Q
、q
(即内、外热源)为恒定值,由此引起的节点温度变化在每次迭代计算中是恒定的。造成节点温度不能收敛的因素来源于式(4)中的第3 项,即节点与其他节点之间的等效热导项。下面分析迭代过程中的等效热导,为求简便,将研究的节点定义为节点0,其他节点为1, 2, …,n
‒1。1)第1 次迭代
在此迭代步骤中,节点0 向其他节点释放的热量为

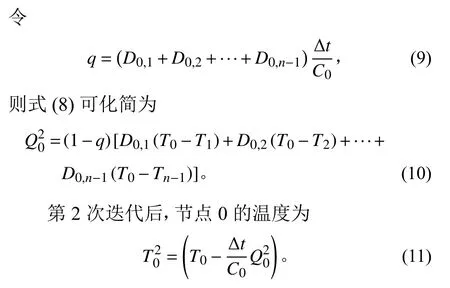
3)收敛性分析
若节点0 为扩散节点,在迭代求解的过程中,其温度结果收敛的条件为:每一次迭代,其温度相对上一步的变化量小于上一步迭代的值。即,若令K
为相邻两步迭代的温度变化量之比,则有
K
与迭代次数无关,说明每一次温度的迭代结果与上一次的差值是一个与迭代次数无关的等比数列。因此,|K
|<1 是节点0 温度结果收敛的充要条件。同时,对节点i
,记D
+D
+ …+D
=D
,有节点i
温度结果收敛的充要条件为
式(13)可叙述为:在迭代法求解过程中,某个节点收敛的充要条件是该节点与其他所有(与之有换热关系的)节点的等效热导之和与计算时间步长的积小于该节点的热容。上述“等效热导之和与时间步长的积”的单位为[(W/K)∙s]即J/K,与节点热容的单位相同。热容的物理意义为“节点温度每变化1 ℃所吸收或释放的热量”,即单位温升热流量。类似地,“等效热导与时间步长的积”的物理意义可以理解为节点与其他节点温差为1 ℃时的热流量,可以将其命名为“单位温差等效热流量”。那么,式(13)可简明地叙述为:某节点收敛的条件是其与其他节点单位温差下的等效热流量小于该节点的热容。
2.3 模型的收敛性与时间步长约束
以上分析是选定模型中的1 个节点进行的,但分析结果对全部扩散节点有效。则,当一个热物理模型的全部扩散节点均满足式(13)时,该模型计算结果收敛。
另外,上述结论也可用于模型时间步长的选定。对某个节点i
,其时间步长应满足
可见,只要采用式(14)对所有扩散节点计算其允许时间步长,选择其中的最小值,即为整个模型收敛允许的最大时间步长。
2.4 时间步长优化选定
由式(12)可知每一次迭代温度结果与上一次的差值是一个与迭代次数无关的等比数列,因此节点i
第m
次迭代的结果为
δ
。截断误差通常需就每个实际算例综合考量而确定:设置较小的截断误差将有助于提高计算精度,但计算量大、收敛过程缓慢、计算耗时长;设置较大的截断误差可以减少计算量、缩短计算时间,但计算精度不高。指定截断误差后,当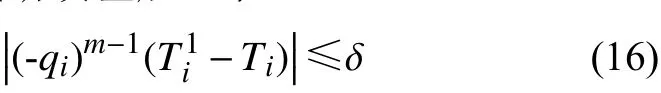
时,认为该节点温度满足收敛条件,停止迭代。
参考式(9)和式(6),对节点i
,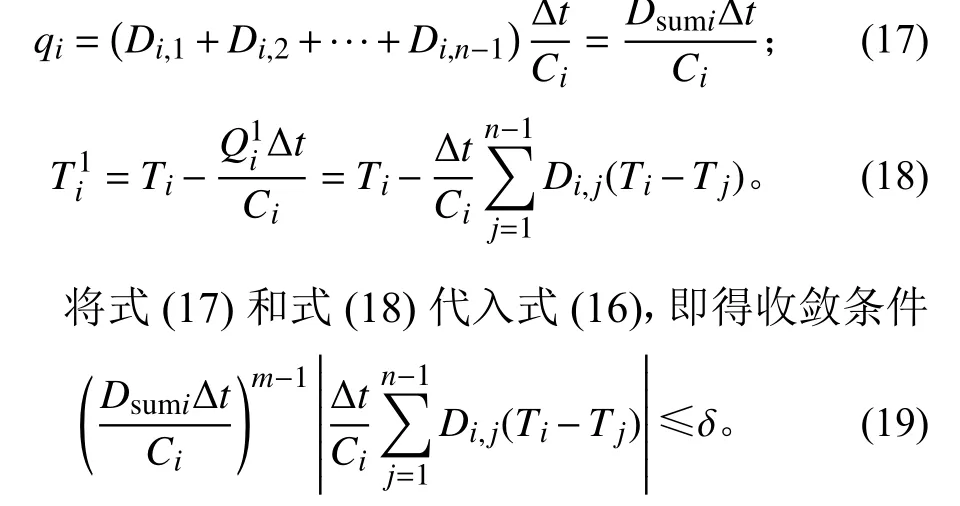
q
的绝对值越接近于1,则式(15)、(16)、(19)清晰表明迭代次数将增多。因此,时间步长的增大,在加快模型时间推进的同时,会增多单个时间步上的迭代次数,对计算效率的影响存在2 种趋势相反的影响,需权衡优化之。式(19)两边同时取自然对数,得到节点i
满足收敛条件的最少迭代次数为
t
越长,模型进展越快;同时,迭代的次数m
越多,计算量越大,消耗的计算时间越长。因此,Δt
/m
是一个表征计算效率的物理量,其物理意义是完成一定计算量所获得的模型进展时间,或可更具体地表达为:完成1 次迭代计算获得的模型进展时间,其单位为s/次。记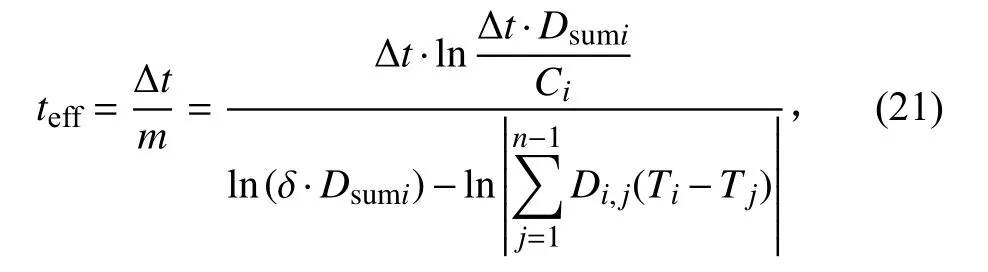
D
、D
、C
等均为定值;T
、T
为计算的起始温度,已知并确定;δ
为计算设定的截断误差,也是确定值。因此,式(21)右侧实际上是一个以Δt
为自变量的形如y
=[x∙
ln(bx
)]/a
的函数。基于以上分析,以Δt
为自变量,t
为因变量,对式(21)求导,可确定t
取最大值时对应的最优Δt
为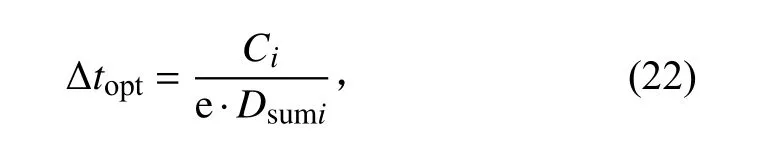
式中e 为自然常数。
通过式(22)可以确定瞬态计算中获得最高计算效率的最优时间步长。对确定的热物理模型,时间步长Δt
的选取决定了计算的效率;对所有满足收敛条件的时间步长Δt
来说,存在一个最优值,使得时间步长取该值时模型计算的效率最高,即t
最大,则此时间步长为该模型该步计算的最优时间步长Δt
。结合式(14)可以看出,若定义满足收敛条件的最大允许时间步长为Δt
,即Δt
=C
/D
,则有
即,迭代法求解航天器热网络方程时,最优时间步长是计算收敛允许的最大时间步长的1/e。
3 算例验证
3.1 收敛条件验证
为验证上述方法的正确性,选取一个典型的航天器热物理模型进行分析。该模型用于模拟一个卫星的小舱,由舱板、设备、多层隔热组件等组成,舱板外侧开设有散热面。模型被划分为40 个节点,其中边界节点2 个、算术节点13 个、扩散节点25 个;这些节点之间有传导和辐射换热关系,共有传导项49 个、辐射项151 个。模型置于空间轨道环境下,其热源包括外热流和设备热耗。
对所有扩散节点的传导和辐射换热关系进行统计,发现其中编号为3015 的节点,按式(14)计算所得的收敛允许时间步长最小。节点3015 代表舱板内表面的一部分,其表面积A
=0.04 m,太阳吸收比α
=0.20,红外发射率ε
=0.87,热容为66.47 J/K。该节点与相邻舱板节点、同一舱板的外侧节点以及其上安装的设备均有传导换热关系;与模型小舱的其他舱板内表面和设备有辐射换热关系。按照上述与其他节点的传导和辐射换热关系,计算节点3015 的等效总热导为D
=4.578 7 W/K,按照式(14)计算,可得确保计算收敛的最大时间步长Δt
=14.52 s。现设置截断误差δ
=1.0×10℃,并采用不同时间步长Δt
对节点3015 进行迭代计算,其收敛情况见图1,图中曲线表示迭代过程中节点3015 的温度结果变化过程。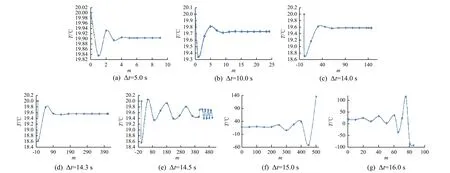
图1 节点3015 不同时间步长下的温度迭代计算过程Fig. 1 Iterative calculation processes for node 3015 with different time steps
从图1 可明显看出,在时间步长Δt
<Δt
时,节点3015 的温度迭代过程很快收敛;随着Δt
的增大,结果收敛需要的迭代次数逐渐增加;当Δt
=14.3 s时,结果收敛需经过410 次迭代;当Δt=
14.5 s(接近Δt
)时,经过500 次迭代,温度结果仍呈振荡状态,不能收敛;当Δt
>Δt
时,迭代结果发散,且Δt
越大,发散速度越快。这样的数据和结果与式(13)理论分析的结论高度一致,验证了理论分析的正确性。3.2 最优时间步长的验证
仍以3.1 节所述模型进行验证。选取不同的时间步长进行迭代计算,结果如表1 所示。表1 列出了选取不同时间步长Δt
时,通过式(20)和式(21)计算得到的理论迭代次数m
和理论计算效率t
,以及实际计算的迭代次数m
和计算效率t
。图2 以曲线形式较为直观地对比了t
和t
随时间步长变化的情况。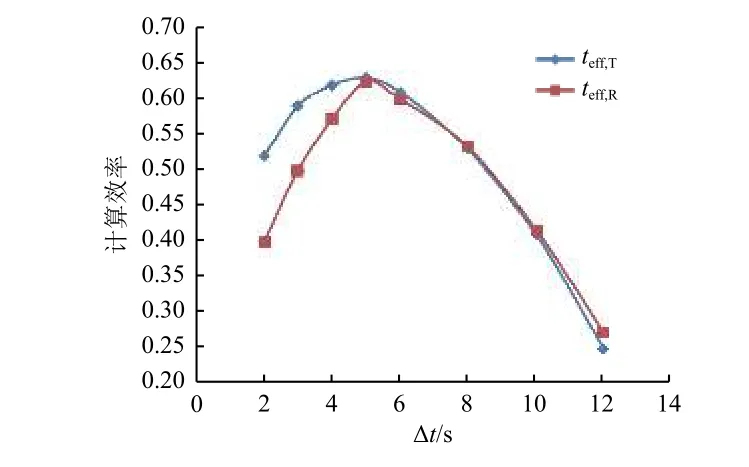
图2 实际计算效率与理论计算效率的对比Fig. 2 Comparison between actual calculation efficiency and theoretical calculation efficiency

表1 采用不同时间步长的迭代计算效率对比Table 1 Results of calculation efficiency with different time steps
从表1 和图2 的结果可见,计算效率最高时的最优时间步长Δt
在5.0~5.5 s 之间。这与通过式(22)和式(23)计算所得的Δt
=14.52/e=5.34 s的结果吻合,验证了2.4 节关于最优时间步长选定方法的正确性。4 结束语
本文采用理论分析的方法对瞬态热物理模型迭代求解过程中的收敛性问题进行研究,获得了节点和模型收敛的条件;并进一步分析时间步长与计算效率的关系,提出了以计算效率为优化目标的最优时间步长确定方法。主要结论如下:
1)对热物理模型的某扩散节点i
,若其与其他节点单位温差下的等效热流量小于该节点的热容,则该节点温度在迭代计算中可收敛,否则不收敛;对于整个模型,若其所有扩散节点满足上述条件,则模型收敛,否则不收敛。2)以上结论的另一种形式为,某扩散节点i
迭代收敛的允许最大时间步长为该节点的热容与等效热流量之比。对模型的所有扩散节点逐一计算其确保收敛的允许最大时间步长,选择其中的最小值,即为保证整个模型收敛允许的最大时间步长。3)在所有满足收敛条件的时间步长中,存在一个最优值,采用该值时计算的效率最高,即1 次迭代计算获得的模型时间进展最大。该最优时间步长为计算收敛允许的最大时间步长的1/e。
需要说明的是,在结果收敛的情况下,即模型所有节点的最终温度结果恒定或接近恒定时,时间步长会影响从初始值走向最终稳定结果的瞬态过程,但不影响最终温度结果。实际在轨航天器的温度往往做周期性波动,在这类航天器的瞬态热物理模型中,时间步长不仅影响瞬态过程,也对最终温度波动范围有影响。关于时间步长对计算精度的影响,受目前研究所限,本文暂不涉及,后续将对该问题开展深入探讨。

