基于卷积神经网络的混凝土裂缝图像识别方法
孟庆成,万 达,吴浩杰,李明健,齐 欣
(1.西南石油大学土木工程与测绘学院,四川 成都 610500;2.西南交通大学土木工程学院,四川 成都 610031)
混凝土结构在服役过程中易出现多种影响结构安全运营和使用寿命的病害,裂缝是最常见的一种。振捣不充分、施工工艺不当、荷载的设置不合理、收缩徐变等都会使混凝土结构产生裂缝[1]。及时发现混凝土结构的裂缝,可为维修养护工作提供依据。截至2019年底,我国铁路里程139 000 km,公路里程5 012 500 km[2]。基础设施规模巨大又以混凝土结构为主,给混凝土结构检修工作带来了严峻挑战,因此需要一种高效准确的混凝土裂缝检测方法应用于检修工作。
随着传统机器学习算法的飞速发展,各国学者基于此对混凝土结构检测方法开展了大量研究。包龙生等[3]通过编写神经网络证明了利用神经网络对桥梁损伤识别的可行性。陈瑶等[4]基于桥梁壁面裂纹,运用小波变换对图像进行处理后使用支持向量机方法实现裂缝分类。魏武等[5]利用小波变换和拉东(Radon)变换提取特征值,使用BP神经网络进行裂缝分类,获得了较高的辨识度。王睿等[6]通过去除两值图像大部分杂质,后建立RBF-SVM算法实现裂缝自动判别,可高效地实现裂缝识别并验证裂缝特征分配的重要性。传统算法若数据量较大,算法性能会受到影响,易出现过拟合,且在提取目标丰富度的能力上低于深度学习。
深度学习作为近年来人工智能领域的新型算法,由于其相对于传统算法的优越性,在工业领域得到了广泛的应用[7]。其概念由G.E.Hinton等[8]于2006年提出,它包含多隐含层和感知层,能更好地描述抽象和深层次的信息。刘新根等[9]使用两个深度卷积神经网络实现了对隧道衬砌和裂缝图像的分类识别。C.V.Dung等[10]利用基于迁移学习的VGG16网络,优化后可对钢桥梁的角撑板节点疲劳裂纹进行识别,相比于原始网络,鲁棒性和准确性均得到了提高。K.Jang等[11]提出使用混合图像的基于深度学习的混凝土裂缝检测技术,使用迁移训练的GoogleNet卷积神经网络,实现裂纹识别和可视化。K.Makantasis等[12]利用深度学习优势,分层构造复杂的特征并利用卷积神经网络构建深层特征,实现了对于隧道结构裂缝的快速预测。王丽苹等[13]在混凝土路面裂缝识别任务中对AlexNet进行优化设计获得了更高的识别准确率。深度学习代表算法之一的卷积神经网络具有表征学习的能力,上述卷积神经网络在混凝土结构裂缝检测任务中仍存在样本数据量较小,不能满足网络模型训练的需要;使用的算法模型出现的时间相对较早的问题,对于图像的处理识别性能相对不足。
基于上述分析,笔者提出一种基于卷积神经网络的混凝土结构裂缝智能检测方法;首先为满足网络模型训练需要,使用数据扩增和图像分割技术建立了较大型的混凝土结构裂缝数据集;然后搭建具有残差结构的18层ResNet卷积神经网络,通过使用不同的学习率策略、批量大小、优化函数以及使用不同迁移学习方式对网络进行优化设计,对比不同超参数下网络模型在混凝土裂缝分类识别任务中的性能;最后使用混淆矩阵从多指标方面对模型性能进行综合评判,验证优化后的网络模型在混凝土裂缝识别任务中的可行性。研究表明:优化后的网络模型可以提高混凝土裂缝识别的准确率,为混凝土维修养护工作提供依据。
1 数据集建立
1.1 数据采集
混凝土裂缝数据采集于已修建完成的五座桥梁结构和七栋建筑结构,选用的拍摄设备为检测人员日常携带的智能手机,共计采集6 d,获得1 216张分辨率为4 032×3 024的混凝土结构混凝土裂缝图像,典型的原始裂缝图如图1所示。

图1 裂缝图Fig.1 Crack diagram
1.2 数据处理
为满足网络模型训练的需要和避免网络模型优化设计中出现过拟合现象,采用数据扩增和图像分割技术对采集到的裂缝图像进行处理,扩增时使用旋转的方法,将原始图像旋转90°和180°,使用图像分割技术将裂缝图片裁剪成分辨率为224×224的统一尺寸,且包含清晰度不同的样本,共获得364 800张包含背景和裂缝的图像,依据清晰度原则进行筛选,筛选后得到27 157张图像,其中14 300张裂缝图,12 857张背景图,按7∶3的比例划分为训练集和测试集,如表1所示。分割后得到的裂缝图和背景图如图2所示。

表1 数据集划分Table 1 Data set division

图2 分割后图像(224×224)Fig.2 Image after segmentation(224×224)
2 混凝土裂缝识别模型
2.1 卷积神经网络
卷积神经网络由卷积层、池化层和全连接层堆叠形成。将裂缝图像作为数据输入网络时,卷积操作会提取图像数据中的有效特征并传递到后面的结构层中,采样层进行特征选择,全连接层对提取的特征进行压缩,以此实现分类的功能,卷积神经网络处理图像数据流程如图3所示。

图3 卷积神经网络数据处理示意图Fig.3 The data processing diagram of convolutional neural network
2.2 搭建残差网络
残差模块[14]的引入可解决堆叠过深的网络出现梯度消失、梯度爆炸或退化等问题。残差模块的数学表达式如下:
yn=h(xn)+F(xn,Wn),
(1)
xn+1=xn+f(yn).
(2)
式中:xn和xn+1分别为第N个残差单元的输入和输出;F(xn,Wn)为网络层学习到的残差;h(xn)=xn时表示恒等映射;f(yn)为激活函数,这里选用ReLU激活函数。
由上述两式可求得当网络深度从浅层n变为深层N时学习到的特征,如下:
(3)
前向计算中简单的堆叠网络层数本质上是乘法计算的性质,残差模块的应用使计算由乘法变为加法,使整个网络计算更加稳定,向后传播时,代价函数为loss时可得到:
(4)
由式(4)可知,更深层次的梯度成分可直接传递到其他网络层,当残差梯度较小时,由于式中1的存在不会导致梯度消失,梯度衰减得到抑制,进一步加强了算法的稳定性。
笔者搭建了18层的ResNet残差网络,该网络主要包含17个卷积层,一个全连接层,其网络结构组成如图4所示。残差模块中使用ReLU激活函数。在网络输出层前使用全局平均池化,该方法的使用可以防止模型出现过拟合现象,增加网络模型的鲁棒性。

图4 网络结构图Fig.4 The structure diagram of network
2.3 ReLU激活函数
笔者使用的ReLU激活函数,具有的单侧抑制、稀疏激活性等特点相比于Sigmoid和Tanh激活函数具有更好的收敛速度和计算效率,数学表达式如下:

(5)
函数图像如图5所示,由其分段函数的性质可知,ReLU函数会令所有小于等于零的数值都变为零,大于零的部分则保持不变。

图5 ReLU函数图像Fig.5 ReLU function image
2.4 超参数
超参数对于卷积神经网络运行效果的优劣有着重要的影响,不同超参数的选取以及组合在很大程度上决定了网络训练时间、收敛速度等,笔者主要选取学习率(Learning rate)、批量大小(Batch_size)和两种优化函数进行组合,在使用和不使用迁移学习两种情况下运行笔者所搭建的网络模型。
2.4.1 学习率
学习率是一种与目标函数能否收敛以及收敛时间有关的超参数。当学习率的值设置过大时,会导致整个网络无法收敛,当学习率设置较大时,会出现整个网络振荡收敛的结果。文中设置两种学习率下降方式,如图6所示,其中学习率策略一是指数衰减式,每迭代一次,学习率衰减0.9,学习率策略二是分段常数衰减式,每迭代10次,学习率衰减0.55,其计算公式:
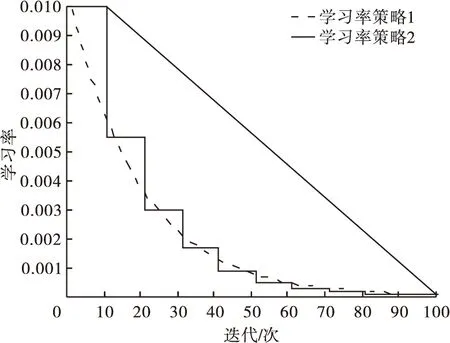
图6 学习率下降策略Fig.6 The reduction strategy of learning rate
new_lr=old_lr×gamma(epoch/step-size).
(6)
式中:gamma为衰减率;epoch为迭代次数;step-size为衰减步长。
2.4.2 批量大小
为保证网络模型可以提取到有效的裂缝信息,结合本次实验所使用的设备,批量大小的取值分别为32和64。设置合理的批量大小可以在设备的内存效率和内存容量之间找到最佳平衡点,提高模型的运行速度。批量取值过小会增加训练时间并使得收敛的难度增加,适当的增大批量值可以加速梯度下降并减小训练过程中振动的幅度。
2.4.3 动量梯度下降优化函数
动量梯度下降(Momentum SGD,M_SGD)是在随机梯度下降算法中引入动量。随机梯度下降(Stochastic Gradient Descent)的本质是求得损失函数的一阶泰勒展开式的近似函数。在随机梯度下降中,每一次迭代只需要保证能够拟合某一个训练样本即可,并且在计算过程中已开始对网络参数进行优化,因此,SGD既可以有效地避免冗余数据带来的干扰,也能够加快网络的收敛速度,计算公式为
(7)
wi=wi-1-α▽w.
(8)
其中,x(1),x(2),…,x(m)为训练集中包含的m个样本,x(j)对应目标为y(j);w为初始参数;▽w为损失梯度;f(x;w)为学习器;α为学习率。
但SGD在应用过程中会出现陷入局部最优解的情况和振荡收敛的问题,为解决这类问题,在SGD优化函数中引入动量(Momentum),动量的加入使得SGD算法在相关方向上加速并抑制其振荡,如图7所示,动量的优化方式如下:

图7 SGD(虚线)和带动量的SGD(实线)Fig.7 SGD(dotted line)and SGD with momentum(solid line)
vt=βvt-1+η▽w,
(9)
wt=wt-1-vt.
(10)
式中:vt为初始速度;β为动量更新值,取经验值0.9。
2.4.4 Adam优化函数
Adam[15]优化函数可对随机目标函数执行一阶梯度优化,适应性低阶矩估计为其理论基础。该算法易于实现,因其执行的是一阶梯度优化故对设备内存需求较少,该函数具有的对角缩放不变性使其适用于数据规模较大或参数较多的问题。其数学表达式如下:
mt=β1mt-1+(1-β1)gt,
(11)
(12)
(13)
(14)

2.5 迁移学习
为防止网络模型在相对较少的样本下出现过拟合的现象,降低对实验硬件设备的需求等,笔者采用迁移学习[16-18]的方法。迁移学习是指将在其他模型训练任务中学习到的角、点、纹理等通用信息应用于新的任务中,迁移学习的方式有多种,笔者中采用两种,第一种为固定卷积层,仅改变最终的全连接层,训练时卷积层参数不变,第二种为仅改变最终的全连接层,训练时更新全部参数,将这两种方式分别命名为TL1和TL2。
3 实验结果分析
3.1 实验设备
实验的设备型号为Intel(R)Core(TM)i7-8700K CPU,16.0GB内存,NVIDIA GeForce GTX 1050 Ti,Windows 10操作系统,Python3.7,深度学习开源框架PyTorch。
3.2 实验结果
实验中将学习率、批量大小以及M_SGD和Adam两种优化函数进行组合,将不同组合模型分别在无迁移学习和不同迁移学习方式下进行训练,运行结果如表2所示。实际环境中光照强度、结构物所处位置、噪声等会影响拍摄图片的质量,图8为模拟实际可能出现的情况,将原图增减亮度以及增加噪声。为验证模型鲁棒性,在第13组实验模型参数基础上对不同处理方式的数据集进行测试,测试结果如表3所示。

表2 结果对比Table 2 Comparation results

图8 图片处理Fig.8 Image processing

表3 不同数据集测试结果Table 3 Test results of different data sets
3.3 结果分析
由表2可以得出:①在超参数组合相同时,使用迁移学习方法二的识别准确率高于迁移学习方法一和不使用迁移学习的组合;②使用迁移学习方法时,使用优化函数M_SGD的识别准确率要高于优化函数Adam;③使用迁移学习方法时,批量大小取值64的网络识别精度优于批量大小为32的网络;④优化函数为M_SGD时,使用学习率策略一的效果优于学习率策略二,优化函数为Adam时,使用学习率策略二的效果优于学习率策略一;⑤第13组参数下的网络在图像质量不同的数据集下得到的准确率值波动较小,证明该参数下的网络具有良好的鲁棒性。
不同超参数组合下网络在使用迁移学习方法二(TL2)进行训练时其准确率和损失值曲线如图9所示,每条曲线按迁移学习方式
(TLn)-学习策略(Lsm)-优化器-批量大小命名。由图9可知,网络在迭代约75次时开始收敛,第13组实验识别准确率最高,此时识别准确率为97.98%。

图9 损失值与准确率Fig.9 The comparation results of loss values and accuracies
4 模型评价
混淆矩阵(Confusion Matrix)又称误差矩阵,可用于图像分类结果的评价。笔者为对所优化的卷积神经网络模型进行更全面的分析,而不是仅采用准确率一个指标,引入了混淆矩阵,通过分别计算分类模型对各类别的识别正确和错误的数量,来反应模型的优劣,混淆矩阵为

(15)
其中,TP表示裂缝数据中模型预测为裂缝的数量,FN表示裂缝数据中模型预测为背景的数量,FP表示背景数据中模型预测为裂缝的数量,TN表示背景数据中模型预测为背景的数量。性能优异的模型TP与TN的数量应足够大,FP与FN的数量应足够小。笔者模型的混淆矩阵结果如图10所示,其中TP和TN很大,FN和FP的数值很小。

图10 混淆矩阵结果Fig.10 Confusion matrix result
根据混淆矩阵的结果定义四个评判模型性能指标,分别为准确率(Accuracy)、精确率(Precision)、灵敏度(Sensitivity)、特异度(Specificity),其表达式如下:
(16)
(17)
(18)
(19)
其中,Accuracy表示模型预测正确的结果占总数量的比值;Precision表示模型预测为裂缝的结果中,模型预测正确的比值;Sensitivity表示真实值为裂缝的结果中,模型预测正确的比值;Specificity表示真实值为背景的结果中,模型预测正确的比值。
根据上述公式,将混淆矩阵的结果值带入上述4个公式中,可以求得本文模型中指标值,其结果如表5所示。由表可以看出,笔者搭建的网络模型具有良好的性能。

表5 指标值Table 5 Index value
5 结 论
(1)迁移学习方式不同,对网络运行结果影响较大,使用正确的迁移学习方式可以有效地提高网络模型识别精度;其他条件相同时,在训练中更新全部参数的模型性能优于不使用迁移学习方法和训练时卷积层参数不变的网络。
(2)当仅改变最终的全连接层,训练时更新全部参数,且超参数组合为:学习率以每迭代一次衰减0.9,批量大小取值为64,优化函数为动量梯度下降时,网络识别准确率最高,且网络具有良好的鲁棒性。
(3)使用混淆矩阵可以对网络模型性能从多个指标进行评判,将混淆矩阵应用到模型性能评价工作中,使用混淆矩阵有效证明了笔者模型在裂缝识别任务中具有优异的实用性能。
(4)在迁移方式和其他超参数相同时,使用M_SGD优化函数获得的效果要优于Adam优化函数,在实际应用中可优先使用M_SGD优化函数。
(5)笔者所提模型经优化后在裂缝识别任务中达到了97.98%的识别准确率,表明优化后的网络模型具有良好的裂缝识别能力,可为混凝土裂缝识别检测提供帮助。

