广义Hoek-Brown准则在某非洲水电工程中的应用研究

刘超杨，郭 果，郭维祥

(1中国水电顾问集团贵阳勘测设计研究院岩土工程有限公司，贵州 贵阳 550081；2中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081)

0 引言

Hoek-Brown准则是目前国际通用的岩体参数取值方法，1980年Hoek.E和Brown提出了节理岩体强度准则(以下简称H&B准则)(式(1))，1994—1995年Hoek等人在进行了大量的试验分析后，基于地质强度指标(GSI)、施工扰动系数(D)得到广义Hoek-Brown准则(式(2))。至2002年最终形成可计算岩体内聚力、内摩擦角、变形模量及隧道、边坡工况差异化围压计算的完整的理论体系。Hoek-Brown准则能够应用岩体实际情况，计算适应于不同工程类别、应力状态以及开挖形式的岩体参数[1-9]。

国内研究人员对Hoek-Brown准则也进行了一些研究，如杨旭(2017)[10]等研究了塔里木盆地依奇克里克区块深部煤层力学参数的反演及开采井临界稳定半径。刘立鹏(2010)[11]等人应用Hoek-Brown准则对岩质边坡进行稳定性分析，同时研究了H&B准则中GSI、mi、D等因子对边坡计算稳定性系数的影响。宋彦辉(2012)[12]等通过玛尔挡水电站对比原位试验抗剪强度和H&B准则计算参数。郭维祥(2017)[13]等人通过锦屏一级水电站、锦屏二级水电站实例分析，验证了Hoek-Brown准则适用于国内水电工程。这些研究都未能将H&B各个参数因子与工程实际详细结合，因此本文在详细介绍H&B准则后，结合非洲某大型水电工程，详细分析H&B准则参数取值的各个因素，获得工程岩体强度参数后，采用Flac3d软件对导流洞K0+209断面和右岸坝肩边坡进行实例分析。

1 H&B准则基本原理

H&B准则适用于完整岩体或发育有三组及以上不连续结构面的岩体，其基本计算公式如下：

(1)

式中：σ1′为岩体破坏时的最大有效主应力，σ3′为岩体破坏时的第三有效主应力；m、s为与岩石材料相关的常数；σci为完整岩石单轴抗压强度。

(2)

隧道工程和边坡工程模拟围压计算公式：

(3)

式中：mi为岩石的H&B常量，可通过三轴试验获得，或查阅文献[5]；GSI(Geological Strength Index)为地质强度指标；D为爆破或应力对岩体的扰动系数，取值可查找文献[9]获得。

2013年Hoek.E在归纳总结Bieniawski 1989年提出的岩体结构面评分标准基础上，采用Jcond89和RQD获得定量计算GSI的方法[14-15]：

GSI=1.5Jcond89+0.5RQD

(4)

2 研究区工程地质特征

2.1 基本地质条件

非洲某大型水电站正常蓄水位184.00 m，设计总装机容量2115 MW，大坝为碾压混凝土重力坝，最大坝高131 m，坝肩边坡最大坡高约120 m，施工导流洞，洞长704 m，最大洞径24.0 m。

工程区地层岩性为Karro系近水平状厚层砂岩及薄层至中厚层泥岩互层，区域构造以正断层为主，水平应力介于0.5～1.0倍竖向应力之间，岩石工程开挖后，未出现任何高地应力地质标志特征，属于低应力区域[16，17]。主要发育J1组(N30°～50°E/ SE80°～85°)、J2组(N40°～60°W/ NE70°～85°)二组节理，J1、J2和岩层面共同对岩体产生切割。

J1组NE向节理裂隙间距0.2～0.5 m，受J2组裂隙影响，裂隙呈阶梯状延伸，单个阶梯0.1～0.3 m，延伸长度一般为0.5～1.0 m，自然状态下为微张开至闭合状，局部可见泥膜，铁质浸染痕迹，整体为微风化至中风化状态。J2组NW向裂隙十分发育，为主导型节理裂隙，裂隙间距0.15～0.3 m，延伸长度1～3 m，节理面平直至稍起伏，光滑至稍粗糙，微张开至中等张开，多为岩屑充填，局部为泥质充填，整体呈微风化至中风化，局部为强风化状态。

坝址区不同高程位置取样微风化和新鲜砂岩、泥岩进行室内试验，同时也在平硐和引水隧洞进水口进行了岩体原位变形和剪切试验，在左岸ZKDL6钻孔和右岸ZKDR5钻孔进行孔内变形模量试验。

2.2 地质指标统计

研究区砂岩、泥岩RQD主要受层理和局部随机节理控制，野外露头、开挖断面或钻孔岩心素描资料分析统计GSI，由于J1、J2组节理均为陡倾角，勘察孔主要为竖直钻孔，因此RQD值较高，主要集中在60%～100%之间，如图1。坝址区Jcond89[10]统计如表1。

图1 坝址区砂岩、泥岩RQD频率分布图Fig.1 Sandstone RQD frequency in dam site area

表1 坝址区岩体节理特征及Jcond89评分Tab.1 Characteristics and Jcond89 score of rock mass joints in dam site area

应用式(4)方法和露头统计法GSI值对比如图2。式(4)方法计算弱风化(中风化)砂岩GSI=50～70，新鲜砂岩GSI=60～80，弱风化(中风化)泥岩GSI=57～77，新鲜泥岩62～82。

图2 式(4)方法和露头统计评分GSI比较Fig.2 GSI comparison of Formulation(4)method and outcropping sketch method

野外露头和各开挖面GSI评分，中风化砂岩GSI=35～55，新鲜砂岩GSI=55～70，中风化泥岩GSI=30～60，新鲜泥岩55～70。

在使用式(4)方法计算GSI时偏高，主要是因为钻孔方向与节理面小角度相交，如坝址区典型钻孔(图3)，岩心完整性与裂隙相关性弱，因而获得的岩心具有较高的RQD值。

图3 ZK505号钻孔岩心Fig.3 Core of ZK505 borehole

3 Hoek-Brown准则计算岩体参数

3.1 H&B 因子mi、σc、D、H

查表[5]得砂岩mi=17，泥岩mi=6。新鲜完整砂岩σc=60 MPa，新鲜完整泥岩σc=40 MPa。坝址区主要岩石工程为隧道和边坡工程，隧洞采用短进尺多循环的台阶法开挖，边坡则采用小规模控制爆破台阶法开挖，扰动因子DT=0.3，计算边坡工程参数时DS=0.7。坝址区隧道为深埋隧道，埋深50～80 m，平均埋深68.0 m，HT=68，坝肩边坡最大高度120 m，HS=100。

3.2 计算参数与现场原位试验对比分析

采用广义H&B准则分别计算原位直剪试验同等围压下砂岩岩体抗剪强度C’、内摩擦角φ’，原位试验结果如表2。

表2 1号平硐、3号平硐中风化岩体原位试验结果表Tab.2 In-situ test results of moderately weathered rock mass at No.1 and No.3 adit

原位试验抗剪强度与广义H&B准则计算值进行比较，如表3。

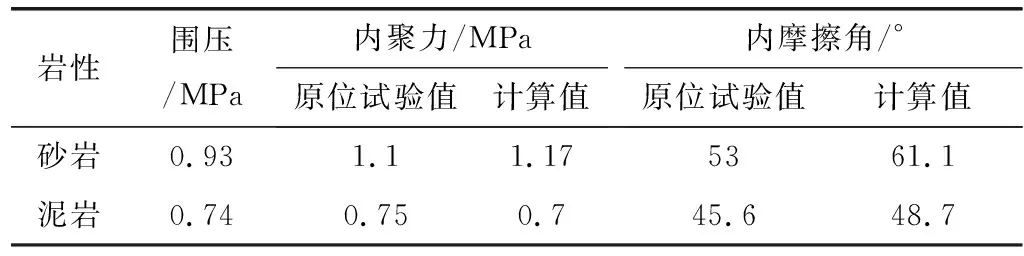
表3 中风化岩体原位试验和H&B准则计算值Tab.3 Data of in-situ test and Hoek-Brown criterion calculation of moderately weathered rock mass

数据对比可以看出，当设定围压相同时，两种方法获得的参数十分接近，说明广义H&B准则计算岩体参数与原位试验吻合度较好。

图4 内摩擦角-围压关系Fig.4 Relationship between friction angle and confining pressure

非参数检验和相关性分析，围压和内摩擦角相关系数r=0.938，显著系数为P=0.037，为显著相关关系。围压和内聚力系数r=0.883，显著系数为P=0.052。总体显示岩体抗剪强度与围压为正相关关系。

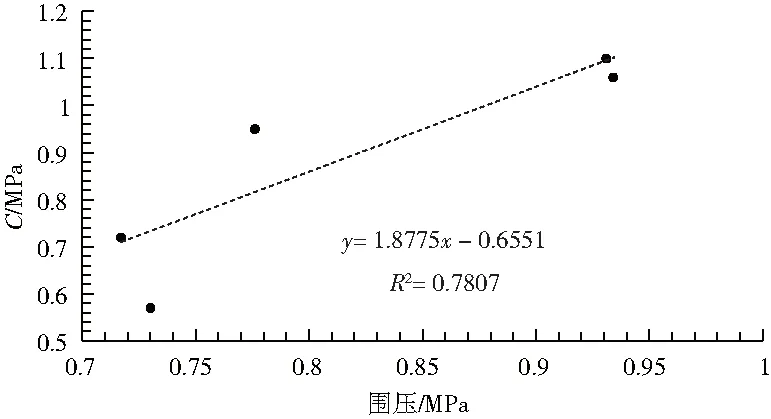
图5 内聚力和围压关系Fig.5 Relationship between cohesion and confining pressure

采用H&B准则在公式(3)计算围压下坝址区隧道和边坡岩体强度参数，如表4。

表4 坝址区岩体强度参数H&B准则计算值Tab.4 Rock mass strength parameters calculated by Hoek-Brown criterion in dam site area

依据不同的工程类别、岩石类别、风化程度以及扰动情况，计算隧道和边坡工程参数与原位试验数据对比，如图6～图8。

图6 岩体内聚力对比Fig.6 Comparison of cohesion in rock mass

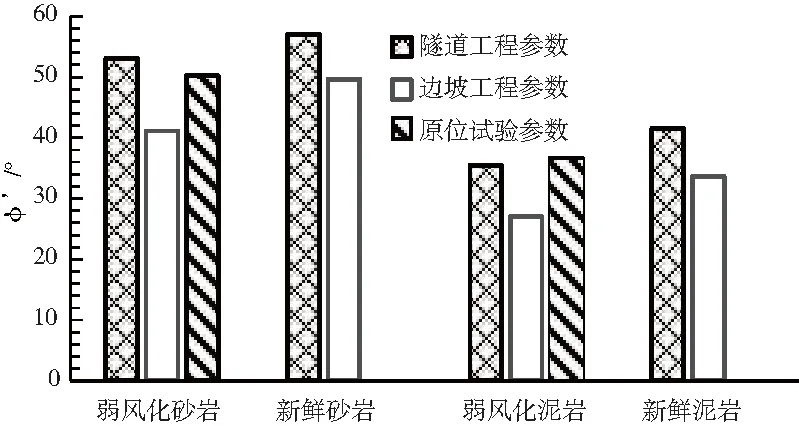
图7 岩体内摩擦角对比Fig.7 Comparison of friction angle in rock mass

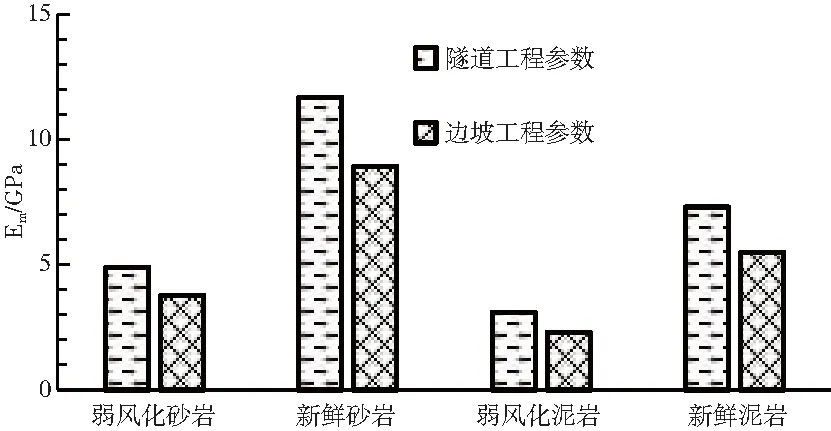
图8 岩体变形模量对比Fig.8 Comparison of deformation modulus in rock mass

从参数对比图可以看出，H&B准则计算值与原位试验值存在明显差异，其原因主要为围压和扰动系数取值差异，参数在不同类型工程使用时，需要区别考虑。

3.3 坝址区岩体弹性模量和变形模量关系

坝址区ZKDL6和ZKdr5号钻孔进行了孔内模量测试，得到岩体的弹性模量和变形模量对应关系如图9。

图9 坝址区弹性模量和变形模量关系曲线Fig.9 Relationship between elastic modulus and deformation modulus in dam site area

非参数检验和相关性分析，岩体变形模量和弹性模量相关系数r=0.71，显著系数P=0.000454，为显著相关，经数据拟合得到关系式(5)。

Ee=0.9689Ed+2.535

(5)

式中：Ee为弹性模量(GPa)，Ed为变形模量(GPa)。

4 隧洞案例数值分析

导流洞全长703 m，分布高程62.7～86.5 m，最大高度22 m，最大洞径24 m，总体坡降0.5%，为门形隧洞。K0+209.0 m断面洞径14.2 m，最大高度19.1 m，分三级开挖，第一级开挖76～84 m，第二级开挖76～67 m，第三级开挖67.0～64.9 m，第一级贯通后依次开挖第二级、第三级，单级循环进尺3.0～5.0 m，开挖设计初支锚杆间距1.5 m×1.5 m，型号φ26 mmHRB400，灌注M35水泥砂浆，梅花形布置，开挖成洞如图10。

图10 导流洞K0+209.0m开挖掌子面第一级开挖Fig.10 First stage excavation of working face in diversion tunnel K0+209.0m

为分析隧洞H&B计算参数的准确性，建立导流洞K0+209.0m数值计算模型如图11，岩体抗剪强度采用广义H&B准则计算参数，弹性模量通过广义H&B准则计算Em值结合公式(5)计算获得。

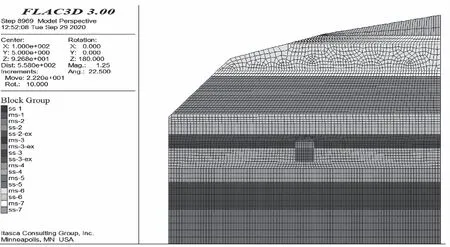
图11 导流洞K0+209.0m数值计算模型Fig.11 Numerical model of diversion tunnel K0+209.0m

砂岩：重度γ=26.0 kN/m3，泊松比μ=0.25，弹性模量Ee=13.9 GPa，内聚力C=0.77 MPa，内摩擦角φ=57°，抗拉强度σt=-0.14 MPa，计算得到体积模量K=9.27 GPa，切变模量G=5.56 GPa。

泥岩：重度γ=25.0 kN/m3，泊松比μ=0.29，弹性模量Ee=9.62 GPa，内聚力C=0.48 MPa，内摩擦角φ=41.5°，抗拉强度σt=-0.11 MPa，计算得到体积模量K=7.63 GPa，切变模量G=3.73 GPa。通过FLAC3D软件计算洞体开挖后隧洞的应力分布和变形，并与监测数据进行对比。

采用更改强度参数的弹塑性求解法模拟初始应力场[18]，隧道开挖面高程第三主应力如图12。

图12 隧道开挖面第三主应力图Fig.12 Contour of the third principal stress

从云图可以看出，隧道开挖断面第三主应力为-1.7～-2.2 MPa之间，第一层开挖后隧洞围岩应力和变形情况如图13。

图13 开挖后Z方向应力图Fig.13 Contour of Z-direction stress after excavation

Z方向应力云图看出，断面开挖后在顶拱、边墙和仰拱出现应力集中。模型计算收敛后顶拱和仰拱位置塑性单元分布，说明开挖后顶拱发生破坏，这与图10所示的顶拱出现典型水平岩层隧洞平顶效应相符[19]。

图14 模型计算收敛后塑性单元Fig.14 Plastic element after calculation

图15 Z方向位移Fig.15 Contour of Z-direction displacement

位移云图显示，开挖后最大位移出现在隧洞拱顶处，Z方向位移量为3.4 mm，现场监测Z方向最大位移值为0.7 mm。计算位移量与实际位移量较为接近，说明该隧洞工程使用广义H&B准则计算岩体参数效果较好。

5 边坡案例数值分析

右岸坝肩边坡岩体结构为砂岩泥岩互层，在坡底河谷位置局部为冲积层和崩积层。坡面共分七级分台阶开挖，最大单级高度16 m，设计坡比1∶0.6～1∶0.8， 83.0 m高程和131 m高程为马道兼施工道路，设计台阶宽10 m，其余均为2.0 m，开挖面岩体状况如图16。

图16 右岸坝肩边坡照片Fig.16 Photo of right bank abutment slope

边坡计算模型如图17，岩体抗剪强度采用广义H&B准则计算参数，弹性模量通过广义H&B准则估算Em值结合公式(5)计算获得。因河流下切，坝基边坡岩体有一定厚度卸荷 ，边坡岩体为弱风化状态。

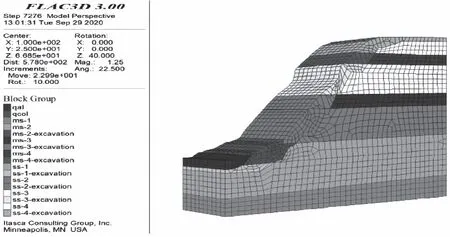
图17 计算模型Fig.17 Numerical model

砂岩：重度γ=26.0 kN/m3，泊松比μ=0.27，弹性模量Ee=6.76 GPa，内聚力C=0.6 MPa，内摩擦角φ=41.1°，抗拉强度σt=0.03 MPa，计算得到体积模量K=4.9 GPa，切变模量G=2.66 GPa。

泥岩：重度γ=25.0 kN/m3，泊松比μ=0.3，弹性模量Ee=4.76 GPa，内聚力C=0.32 MPa，内摩擦角φ=27°，抗拉强度σt=0.09 MPa，计算得到体积模量K=2.27 GPa，切变模量G=1.83 GPa。

冲积层：重度γ=18.0 kN/m3，泊松比μ=0.4，变形模量Ee=30 MPa，内聚力C=0 MPa，内摩擦角φ=34°。

崩积层：重度γ=18.5 kN/m3，泊松比μ=0.38，变形模量Ee=40 MPa，内聚力C=0 MPa，内摩擦角φ=38°，边坡XZ方向初始应力如图18。

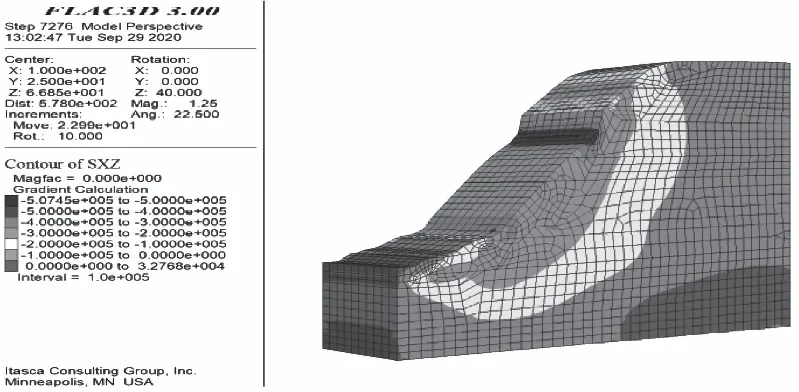
图18 XZ方向初始应力云图Fig.18 Contour of initial stress in XZ-direction

边坡采用逆作法，自上而下逐级开挖，开挖后应力和变形如图19～图22。

图19 开挖后XZ方向应力云图Fig.19 Contour of XZ-direction stress after excavation

图20 边坡开挖完成后主位移云图Fig.20 Contour of principal displacement after excavation

图21 各级边坡X方向位移曲线Fig.21 X-direction displacement of each bench slope

图22 各级边坡Z方向位移曲线Fig.22 Z-direction displacement of each bench slope

由应力云图可看出，边坡开挖后应力重新调整，马道位置出现局部应力集中，同时主位移云图可以看出边坡开挖后在各级边坡边缘处位移最大。

从位移曲线可以看出，X方向最大位移为第二级马道位置，位移量为1.32 mm，Z方向最大位移出现在第二级、第三级边坡，最大位移量4.7 mm。结合Z方向位移分析第七级边坡开挖后，第四～第七级边坡X方向位移转为负值，而Z方向位移均为正值，说明边坡开挖后水平向及竖直向应力释放调整，岩体向临空面卸荷回弹[20]。边坡开挖完成后单元状态可以看出，边坡并未产生贯通性塑性破坏，其破坏主要集中在各级边坡坡面浅表层。

图23 开挖后塑性单元分布Fig.23 Plastic elements distribution after excavation

综上可知，右岸坝肩边坡开挖后整体稳定性好，不会产生大规模岩体破坏，但是在各级边坡开挖后，地应力发生调整，各级边坡表层产生卸荷回弹。为了保证坝肩岩体质量，边坡开挖后应在各级边坡浅表层施加保护措施。

6 结论

1)应用广义H&B准则计算岩体抗剪和变形模量参数，需要系统地分析计算所涉及的各个指标，不同的工程类别和施工形式需要区别考虑。

2)式(4)方法不适用计算节理产状均为陡倾角的节理岩体GSI，计算这类岩体时需要分析岩体嵌锁效果和结构面条件进行定性评分。

3)坝址区砂岩、泥岩广义H&B准则计算参数和原位试验参数在同等围压条件下数据对比，说明广义H&B准则与原位试验有较好的吻合度。

4)应用广义H&B准则计算参数对坝址区引水隧洞模拟分析，模拟结果显示的隧洞顶拱位移与现场相符，隧洞顶拱出现的应力集中及围岩单元塑性单元分布，与现场隧洞出现的平顶效应一致。

5)应用广义H&B准则计算参数对坝肩边坡开挖过程进行数值模拟，边坡开挖后整体位移较小，主要为坡体开挖后表层岩体卸荷回弹，这一现象与实际相符。

6)研究区为低地应力区，原位试验及数值模拟对比分析表明广义H&B准则在低应力地区有较好的适应性。

使用目前国际通用的广义H&B准则岩体参数取值方法，能够很好地适应水电工程岩体参数取值。