基于模糊相似优先比的供水管网渗漏同步诊断*

武佳佳，马东辉，2，王 威，2

(1.北京工业大学 城市建设学部，北京100124； 2.北京工业大学 抗震减灾研究所，北京 100124)

0 引言

城市供水管网发生渗漏和爆管时常常难以发现，造成水资源浪费并影响居民日常生产生活用水。此外，强震极易破坏管道，不仅影响灾时救援和灾后居民生活，还可能引发次生火灾[1]。因此，研究管网的漏损定位及漏损程度诊断对节约水资源以及灾后救援安排尤为重要。

目前，研究渗漏监测定位方法主要有基于监控系统实时数据的方法，基于水力瞬态变化分析的方法，基于模型的方法以及基于优化算法的方法等。Misiunas等[2]提出1种集成了压力连续监测和水力瞬态计算的给水管网突发事件检测和定位算法，但该方法仅适用于瞬态压力波引起的中大型渗漏；Palau等[3]采用主成分分析法将重要信息合成统计模型探测供水管网的大部分渗漏；曹欣欣[4]采用粒子群优化支持向量机(PSO-SVM)模型实现渗漏位置和渗漏程度的同步诊断；Mounce等[5]利用人工神经网络对传感器产生的时间序列数据建立经验模型；陈海等[6]基于人工神经网络建立渗漏位置与压力监测变化率之间的非线性关系实现渗漏定位；Zhang等[7]利用多级支持向量机(M-SVM)对大型管网进行泄漏区域的识别；程伟平等[8-9]基于监视控制和数据采集的监测资料对渗漏定位进行研究，根据渗漏前后监测数据的变化判断渗漏并计算渗漏可能出现的位置。对于渗漏定位和识别的研究目前已得到较大进展，但关于渗漏位置与渗漏程度的同时检测的研究较少。

范例推理已经在各个领域进行成功的应用[10-12]。对于渗漏定位的问题，基于范例推理的模糊相似优先比方法可以对目前发生的渗漏事件，推理至易渗漏的历史渗漏事件，从而实现渗漏定位及渗漏等级预测。故本文提出基于模糊相似优先比的渗漏诊断方法，通过调用最新版EPANET软件进行压力驱动水力分析，利用扩散器节点来模拟渗漏事件；通过生成压力灵敏度矩阵，采用K均值聚类法进行监测点布置；以渗漏模拟的监测点压力变化值为参数作为源范例，对新的渗漏事件进行范例推理实现渗漏定位及渗漏程度的同步诊断。

1 基于模糊相似优先比法渗漏诊断

1.1 模糊相似优先比

假设T为由k个对象组成的集合T={t1,t2,…,tk}。令∀ti,tj∈T(i,j=1,2,…,k)，与对象t0进行比较，则模糊相似优先比矩阵如式(1)所示：

R=(rij)k×k,rij∈[0,1],(i,j=1,2,…,k)

(1)

式中：R为模糊相似优先比矩阵；rij为对象ti与对象tj同对象t0的模糊相似优先比；k为对象总数。

rij满足以下条件：1)rii=0，2)rij+rji=1(i≠j)。条件表明：在与对象t0的相似程度比较中，ti与ti相比，无所谓优先，故rii=0；若ti比tj的优先程度为rij，则tj比ti的优先程度为rji=1-rij；若rij=1，表明ti与tj相比，同t0相似得多；若rij=0.5，表明ti与tj同t0的相似程度相等。

1.2 渗漏监测范例

1.2.1 范例库表示

设供水管网发生了z个渗漏事件，n个监测点的水压变化值为一离散z行n列的因素空间，将其作为历史渗漏事件源范例库如式(2)所示：

(2)

新渗漏事件目标范例如式(3)所示：

(3)

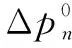
1.2.2 范例属性间的相似性度量

本文以语义距离来表示范例属性间的相似性，采用海明距离公式。语义距离可以表示属性的相似程度，语义距离越小表示2个范例的属性越相似。将单个监测点的压力变化值作为属性，设渗漏源范例为Hps，H0为新渗漏事件的目标范例，则Hps的第j个属性与H0的第j个属性之间的语义距离如式(4)所示：

(4)

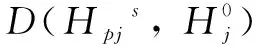
1.2.3 模糊相似优先比关系构造

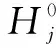
(5)

式中：rpqj为目标范例H0与源范例Hps、源范例Hqs的在第j个属性上的模糊相似优先比；D(Hqjs,Hj0)为历史渗漏事件源范例Hqs和新渗漏事件目标范例H0在第j个属性之间的语义距离。

(6)

式中：Rj为属性j的模糊相似优先比矩阵。

约定与目标范例Hj0最相似的源范例Hpjs排在最前面，顺序号为1；接下来最相似的源范例序号为2，以此类推，最后可得属性j源范例的序号集sj={s1j,s2j,…,szj}T,将所有属性计算完可得到源范例相似程度矩阵，如式(7)所示:

(7)

式中：S为源范例相似程度矩阵；szn为第z个源范例的第n个属性与目标范例的第n个属性的相似程度序号。

最后，结合属性权重计算所有源范例的相似程度值，如式(8)所示：

(8)

式中：Y为相似程度值向量，其中最小值对应的范例号即为与目标范例最相似的源范例；ωj为属性j的权重值。

1.3 影响因素权重的确定

权重用来衡量各影响因素的相对重要性，考虑到不同监测点所监测到的压力变化值在反映渗漏信息时所占的比重不同，本文采用熵权法[13]计算不同监测点的压力变化值所占权重。由于篇幅限制，熵权法原理不再介绍。

2 基于EPANET的渗漏模拟

通过EPANET V2.2[14]模拟渗漏，首先删除或关闭原管道，在原管道渗漏位置添加扩散器组件，然后添加新管道与起止节点和扩散器节点相连，新管道的相关参数，如：管道直径、粗糙度系数、局部水头损失系数与原管道相同[15]，管道添加扩散器示意如图1所示。

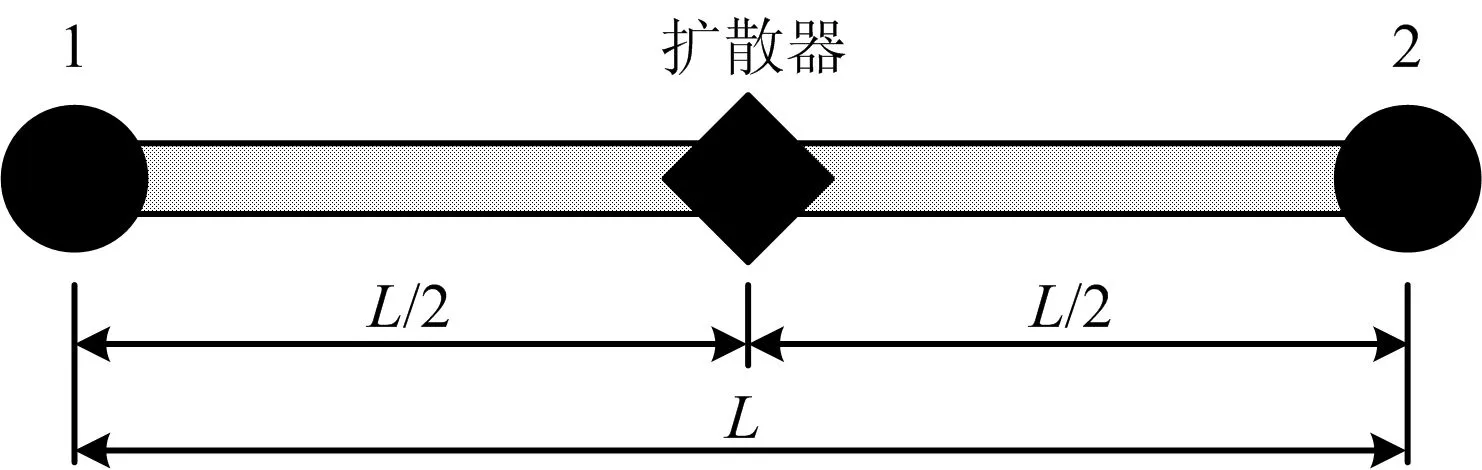
图1 管道添加扩散器示意Fig.1 Schematic diagram of adding diffuser in pipeline

通过扩散器的流量是节点压强的函数，如式(9)所示：

q=Cpγ

(9)

式中：q为扩散器流量，L/s；p为压力水头，m；C为流量系数；γ为压强指数，对于喷嘴取0.5。

要实现渗漏流量的控制，就要确认扩散器流量系数的大小。首先在渗漏管段添加扩散器，删除原管段，添加2个新管段，设置基本需水量为0 L/s，进行压力驱动水力分析后得到扩散器节点的压力值p，设置扩散器流量即渗漏流量，根据公式(9)反算出扩散器的流量系数。通过遍历所有管段，最终得到所有管段发生特定渗漏流量后的各节点压力值。将节点压力值归一化作为压力灵敏度矩阵的元素，采用K均值聚类法[16]进行传感器布置，以距离聚类中心最短欧式距离的样本作为监测传感器布置点。

MATLAB调用EPANET V2.2模拟渗漏事件的流程如图2所示。本文的研究主要步骤如图3所示。

图2 MATLAB调用EPANET V2.2流程Fig.2 Flowchart of MATLAB calling EPANET V2.2

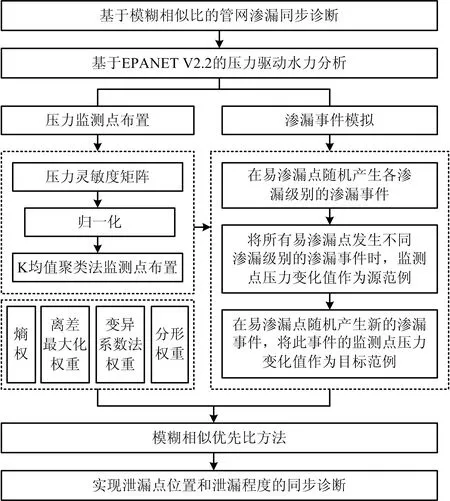
图3 研究主要步骤Fig.3 Main steps of research

3 案例分析

该城市供水管网是根据某地区实际数据建立的模型[17]，共53个节点，78条管段，其中节点1～49为连接节点，节点50为水库，节点51～53为水源节点，该供水管网总供水能力5 992 L/s，如图4所示。

图4 供水管网模型Fig.4 Model of water supply pipeline network

3.1 扩散器系数计算

以管段78为例，在管段78中间添加扩散器，设置其基本需水量为0 L/s，删除原管段，增加2段新管段，新管段参数设置同原管段相同。运行水力计算得到新增扩散器节点的压力水头为19.707 4 m。当设置渗漏流量分别为5，10，15，20，25 L/s时，扩散器节点的扩散器系数及实际需水量见表1。

由表1可以看出，通过设置扩散器系数可以实现渗漏流量的设置。经过PDA水力分析后实际需水量与所设渗漏流量存在一定误差，且随渗漏流量的增大而增大。最大误差在3.68%，本文认为采用该方法模拟渗漏是可行的。

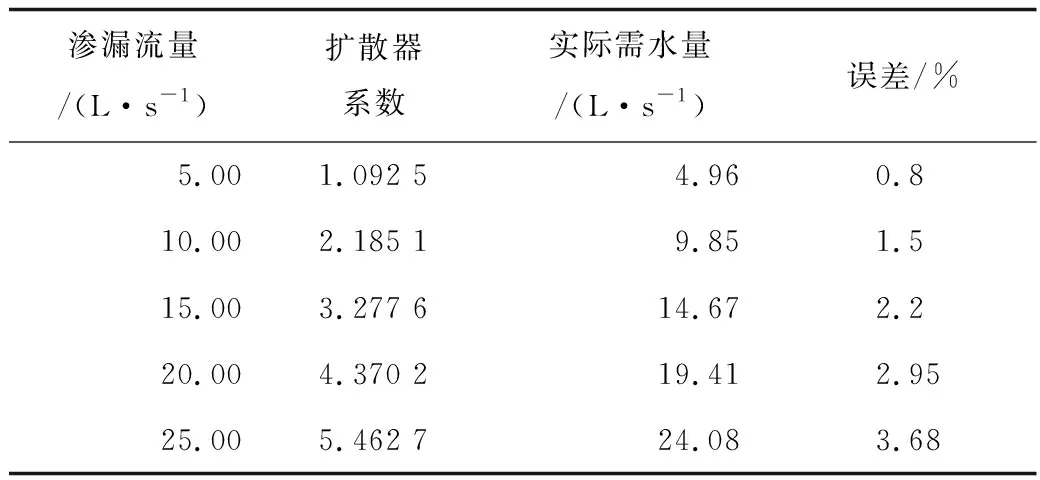
表1 不同渗漏流量扩散器系数及实际需水量Table 1 Diffuser coefficient and actual water demand under different leakage flow rates

3.2 监测点布置

对管网数据进行水力分析。管网监测点的设置应约为节点总数的1/7～1/6，并且大型管网监测点数要小于小型管网[18]，故取该管网节点总数的1/7，约为7个。本文以渗漏流量为30 L/s的压力敏感度矩阵(其中行为节点号，列为管段号)输入到K均值聚类法，类别设为7，将每类的聚类中心，即节点号作为传感器放置的位置。最终监测传感器放置为节点3，9，27，29，34，39，43，如图5所示。

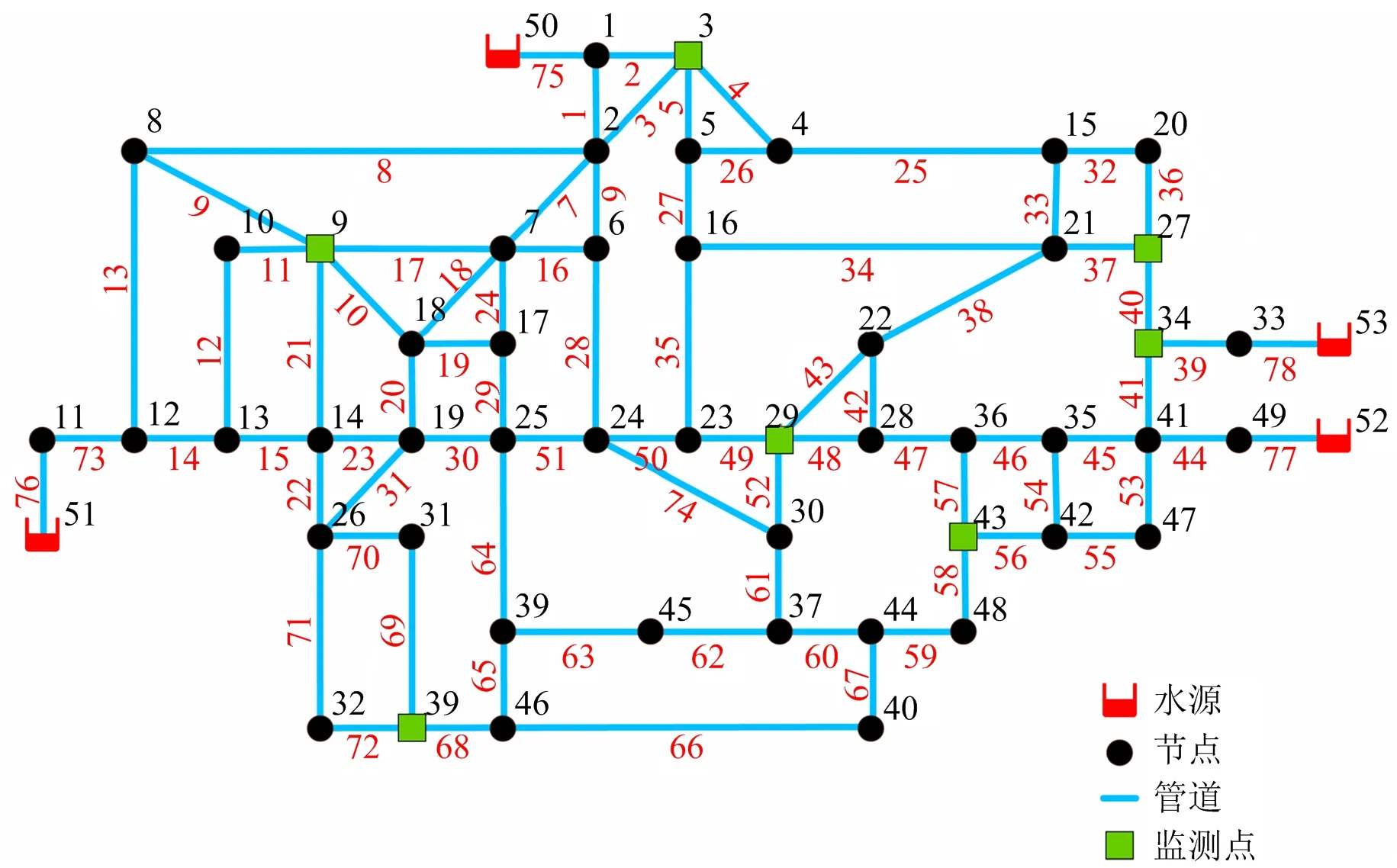
图5 基于K均值聚类法的监测点布置Fig.5 Monitoring points arrangement based on K-means clustering method

3.3 渗漏位置与程度同步诊断

由于同时发生2个或2个以上的渗漏概率较小，因此考虑只有1个管段发生渗漏的情况。本文假设10个易渗漏管段，利用MATLAB产生10个随机数作为渗漏管段号，分别为20，21，26，38，40，45，56，57，69，75，如图6所示。

图6 易渗漏管道分布Fig.6 Distribution of leakage prone pipelines

由于渗漏流量大时，根据监测数据诊断渗漏的结果均较为准确，为探究方法的准确性，本文假定程度较小的渗漏事件，以5 L/s为步长定义渗漏级别，分别为5，10，15，20，25 L/s，对应5种渗漏级别，调用EPANET V2.2进行水力计算，以K均值聚类法得到7个监测点的压力变化值为例，共计50个渗漏模拟方案，见表2。将50组模拟方案作为源范例，假设这10个管段容易发生渗漏事件，在这10个管段中随机产生5个管段，分别为管段38，57，45，26，20，模拟产生新的渗漏事件，渗漏流量分别对应5种渗漏级别，分别为4.8，9.7，14.8，19.6，23.9 L/s，对应源范例序号为：44，38，26，13，1。

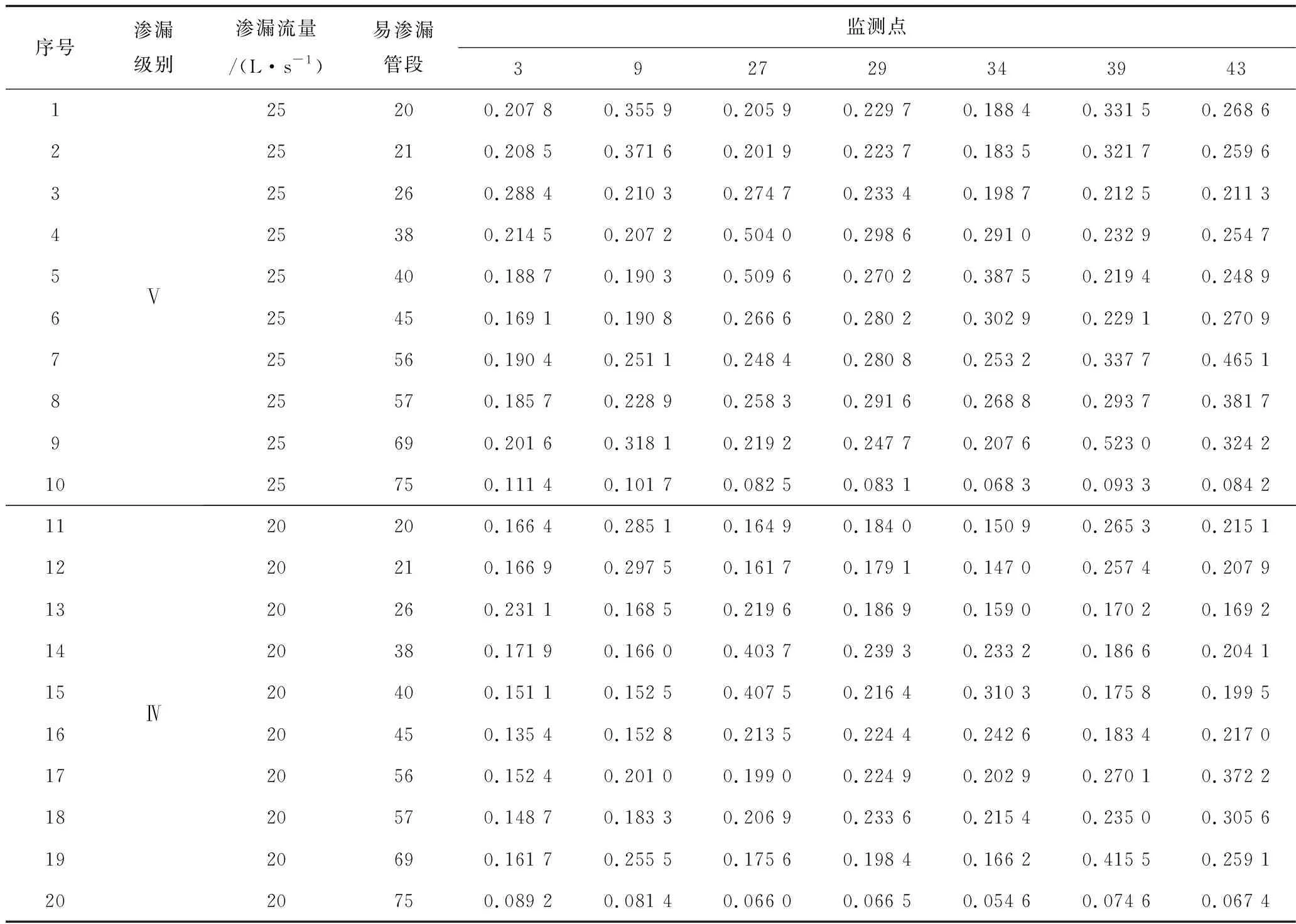
表2 源范例渗漏事件Table 2 Source samples of leakage events

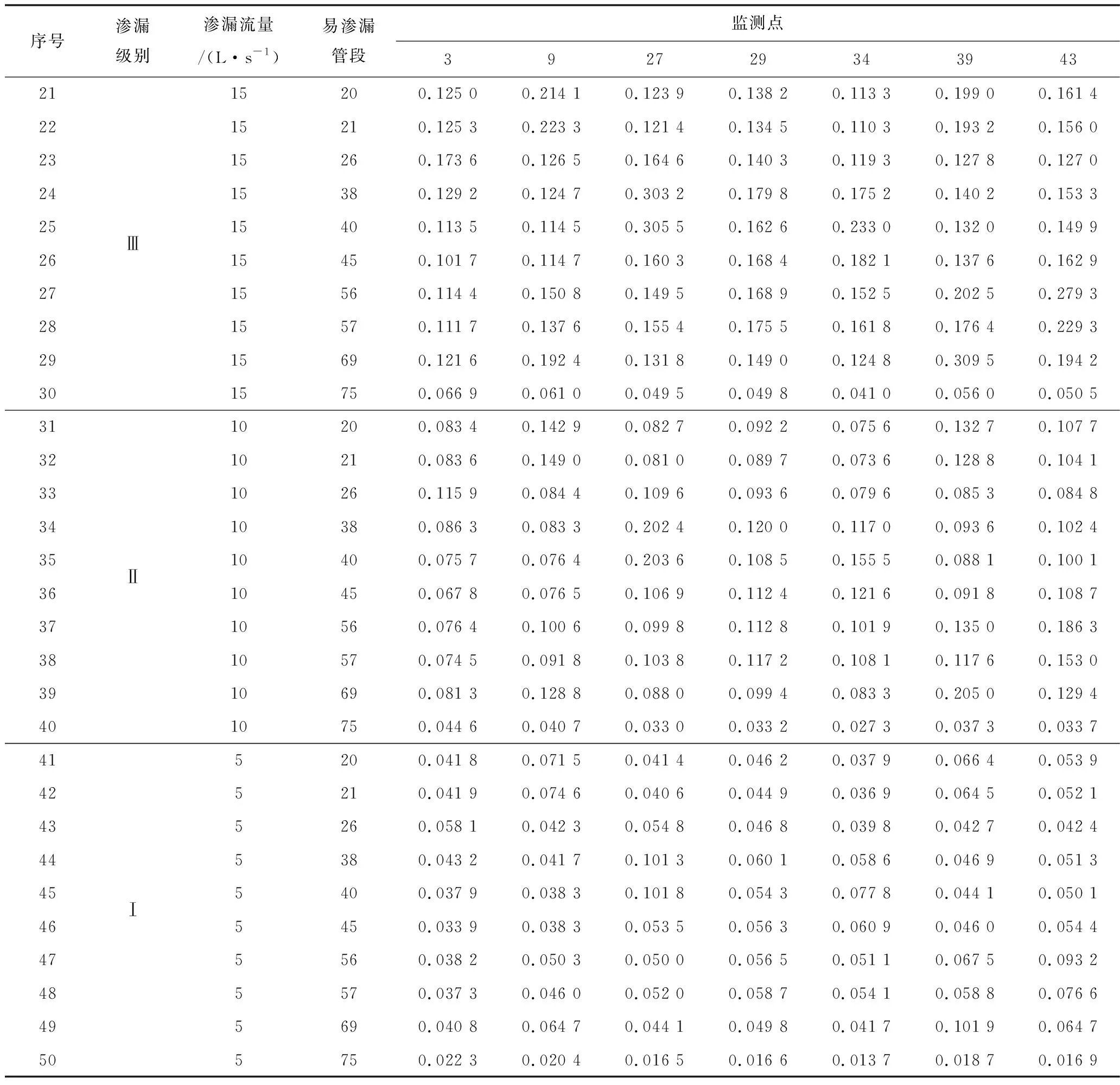
表2(续)

将这5个渗漏事件作为目标范例，采用基于模糊相似优先比的渗漏诊断方法，匹配源范例，并采用3种权重计算方法与熵权法进行对比，计算每个监测点的权重占比，如图7所示。

图7 4种权重方法权重值Fig.7 Weight values of four weighting methods

最后得到5个渗漏事件对应源范例序号，预测结果对比见表3。

由表3可以看出，渗漏流量为23.9 L/s，渗漏级别为Ⅴ，实际渗漏管段20对应源范例序号为1，基于模糊相似优先比的管网渗漏预测方法得到的预测结果与实际结果存在一定误差，但在预测流量级别上准确。采用熵权法赋予权重的预测结果与其他3种权重方法的预测结果相比，相差不大，可用来赋予监测点压力监测变化值的权重。

表3 预测结果对比Table 3 Comparison of prediction results

4 结论

1)通过调用EPANETV2.2添加扩散器的方法模拟渗漏，设置渗漏流量与实际进行PDA水力分析后得到的实际需水量存在一定误差，在可接受范围内，所以采用本文提出的模拟渗漏的方法是可行的。

2)通过模拟易渗漏点发生渗漏事件，采用基于模糊相似优先比方法，可以同步预测渗漏位置及渗漏程度，为渗漏诊断提供新的思路，但该方法存在一定局限性，依赖于源范例的样本规模，源范例越多，预测越精确。下一步研究应考虑其他管网因素对渗漏预测的影响，如管网规模、监测点布置等，为管道更新提供依据。

3)通过对比3种权重方法，发现熵权法所得权重与其他3种权重方法所得预测结果均相同，可以采用熵权法来赋予不同监测点的客观权重。