基于代表的交叉验证分类
王 轩,顾 峰,闵 帆,孙远秋
(1.西南石油大学 网络与信息化中心,成都 610500;2.西南石油大学 计算机科学学院,成都 610500;3.西南石油大学 人工智能研究院,成都 610500)
0 引 言
分类是机器学习的重要研究课题之一。近年来,分类技术在众多领域得到广泛应用。Zhang等[1]在2015年提出了基于代表的邻域粗糙集覆盖分类算法(representative-based classification through covering-based neighborhood rough sets, RCCNRS),自算法提出以来,刘福伦[2]结合6种相似度计算方式,研究了相似度对算法的分类影响;结合代价敏感[3]和主动学习[4]的研究,使算法分类性能得到提升,更贴近实际应用。本文的前期工作对算法的5种标签预测策略进行了对比。
在分类问题上,RCCNRS算法能取得较高的分类精度。然而,在监督式学习中,训练样本的不同,或直接影响分类结果,或通过构建过拟合/欠拟合的分类模型间接影响分类结果。比如,对于RCCNRS算法而言,训练集分割时导致的数据类别不平衡可能会导致数据集的观测几率发生变化,进而影响对未分类样本的分类,影响算法最终的分类精度。
单个分类通常存在分类偏好,对此,集成学习[5-6]的概念被提出。集成学习通过结合多个分类器,组成多分类器系统来完成学习任务,通过均衡各分类器的分类偏好,往往能取得较满意的性能。集成学习有同质集成和异质集成2种策略。同质集成策略,指参与集成的“基分类器”是同种类型但拥有不同参数的个体分类器;异质集成策略,指参与集成的“组件分类器”由不同的算法生成。
针对上述情况,结合集成学习,本文提出基于k-fold交叉验证[7]的3种策略。提出3种集成策略以期限制数据类别不平衡对RCCNRS分类精度的影响,提高分类器的性能。实验在UCI[8]的Chess, Kr-vs-kp, Mushroom, Voting 4个标准数据集上进行。
1 理论基础
本文的研究在于提升基于代表的粗糙集覆盖分类算法的分类性能。
1.1 基础概念
定义1(决策信息系统) 决策信息系统S为一个三元组,定义为
S=(U,C,d)
(1)
(1)式中:U是整个论域;C表示条件属性集合;d表示决策属性。
定义2(邻域) 任意x∈U,设置相似度阈值θ,θ∈(0,1],那么定义样本的邻域为
n(x,θ)={y∈U|sim(x,y)≥θ}
(2)
(2)式中,sim(x,y)表示样本x,y之间的相似度。

(3)
定义4(距离) 设x是待分类样本,它与代表r之间的距离定义为
(4)
定义5(有效代表集合) 待分类样本与距其最近的代表保持决策一致。与待分类样本拥有最小距离的所有代表所组成的集合称为有效代表集合。设选出的代表集合为R,有效代表集合记为
E={r∈R|distance(x,r)=mindis(x,R)}
(5)
(5)式中,
mindis(x,R)=min{distance(x,r)|r∈R}
(6)
1.2 RCCNRS算法
本文的研究基于RCCNRS算法。RCCNRS算法主要分为2个阶段,分别对应代表选举和预测标签2个子算法。
代表选举算法的目的是选出具有代表性的样本。被选出的样本将作为代表,对接下来所有的待分类样本进行分类。算法的伪代码如下。
代表选举算法
输入:S={U,C,d}。
输出: 代表集合R。
1)R=φ;
2) 计算sim(x,y);
3) for(eachx∈U)do

5) end for
6)U/{d}={X1,X2,…,Xk};
7) for(i=1 tok)do
8) whileX≠φdo
9) 选择其邻域对当前论域覆盖最多的x;
10)Ri=Ri∪{x};
11)X中去除r对应的邻域;
12) end while
13)R=R∪Ri;
14) end for
15) returnR;
标签预测算法根据代表选举阶段选出的代表进行分类。最基本的原则是有效代表集合决定其类别标签。算法伪代码如下。
预测标签算法
输入:未分类样本x, 代表集合R。
输出: 预测出的类标签d′(x)。
1)E=φ;mindis=MAX_VALUE;
2) for(eachr∈R)do
3) Computedistance(x,r);
4) if(distance(x,r) 5)mindis=distance(x,r); 6)E={r}; 7) else then 8)E=E∪{r}; 9) end if 10) end for 11) 根据E得到d′(x)并输出; 集成学习通过均衡各分类器的分类偏好,以期获得更好的分类模型。集成学习认为,对于某一分类器的错误预测,其他分类器能够对其进行纠正或者限制。常见的集成学习方法有Bagging[9]以及随机森林法[10](random forest,RF)。 针对单一分类器存在分类偏好的特点,集成学习的概念被提出。集成学习有同质集成和异质集成2种策略。同质集成策略,指参与集成的“基分类器”是同种类型但拥有不同参数的个体分类器;异质集成策略,指参与集成的“组件分类器”由不同的算法生成。本文算法采用同质集成策略。 使用传统监督学习方法分类时,训练集样本越多分布越均匀,分类效果往往越好。在许多实际应用场景中,标记样本代价往往较高,且被标记的样本较少。主动学习提供了使用较少的训练样本,获得性能较好的分类器的方法。 主动学习使用已标记样本,以不确定性和差异性为准则,辅以定制化的策略,甄别当前最有价值的未标记样本。交由专家标记后,补充进训练集,然后重新构建分类器。如此迭代,通过交互式学习不断提高分类器的健壮性,直至触发终止条件。 k-fold交叉验证的基本思想是将原始训练集分成k份,轮流将其中的1份作为测试集,其余作为训练集。以此类推,可以得到k个子分类器。以此进行交叉验证,达到减少随机误差的效果。 本节将详细介绍本文提出的3种交叉验证策略。集成策略1旨在依靠交叉验证提高RCCNRS算法分类精度,简称ERC1;集成策略2去除分类精度低的基分类器再进行集成,简称ERC2;集成策略3借鉴主动学习的思想以扩充训练集规模,来提高分类模型性能,简称ERC3。 ERC1的集成思想是采用委员会投票(query by committee, QBC)决定待分类样本标签。采用k-fold得到的k个子分类器作为同质QBC成员。ERC1是利用交叉验证的方法,限制类别不平衡对RCCNRS算法分类精度的影响。 ERC1的基本框架如图1。原始训练集Tr被分成k份,对应训练成k个子分类器。k个子分类器一起组成委员会,委员会通过投票对原始测试集Te进行标签预测。样本全部获得预测标签后,验证得出算法最终精度。 图1 ERC1框架 ERC2在ERC1的基础上对QBC成员进行了筛选。区别在于,对每一个子分类器,判断其分类精度是否大于原始的RCCNRS算法。如果大于原始算法分类精度,则子分类器成为QBC成员,否则无权成为QBC成员。最终由QBC成员对所有待分类样本进行分类,结果由其投票决定。 ERC2的基本框架如图2。采用k-fold训练子分类器的部分同ERC1,图2未重复展现。委员会中包含分类精度大于RCCNRS分类器的子分类器以及原始RCCNRS分类器。测试集中的待分类样本标签,由委员会投票决定。特殊情况下,当子分类器分类精度都小于原始RCCNRS分类器,则仍用原RCCNRS分类器进行分类。 图2 ERC2框架 在ERC1,ERC2的基础上,受到主动学习的启发提出ERC3对训练集扩容。ERC3认为所有子分类器决策一致的样本适合采用RCCNRS进行标签预测。经过委员会分类后,无条件相信其分类是正确的,用这种方式扩展训练集。具体方法是对原始测试集用QBC进行预分类,将决策一致的样本加入到原始训练集,组成新的训练集。利用新的训练集构建RCCNRS分类器,再对原始测试集分类。相比RCCNRS算法,ERC3主动学习自身认为分类正确的样本。 图3 ERC3框架 本小节将展示所用数据集上的实验结果,并进行分析。实验先进行了k-fold交叉验证,对比不同k值下3种策略的效果,以期寻找出最优的k取值。接着,取实验效果好的k值,将本文提出的3种策略和RCCNRS算法作对比。本文仅研究了二分类问题,实验所用数据集如表1。 表1 数据集描述 每个数据集上共进行10组实验,每组实验重复100次,得出分类精度后取平均值,以减小实验误差。对于Chess,Kr-vs-kp,Mushroom这3个较大数据集,第1组实验取数据集的0.01作为训练集,以后每组实验训练集规模递增数据集的0.01。对于较小数据集Voting,第1组实验取数据集的0.05作为训练集,以后每组实验训练集规模递增数据集的0.05。 对于k-fold交叉验证,k取值不同时,对实验结果影响不同。该部分对k-fold交叉验证的k取值做了实验对比,以期找到本文提出的3种策略的最佳交叉验证k值。 当k取1时没有研究意义,因此,实验中设置k∈{2,3,4,5,6,7,8,9,10}。每一个k值分别在4个数据集上进行实验。不同k值对比如图4。其中,图4a—图4d分别表示在Chess,Kr-vs-kp,Mushroom,Voting等4个数据集上的实验结果,横轴表示k的取值,纵轴表示此时方法对RCCNRS精度提升的平均值。 图4 不同k值对比 根据本文实验结果,在所用的4个数据集上,3种改进策略基本上都是在k=5时取得最好的提升效果。只有ERC3在Mushroom和Voting数据集上,是k值取10时获得最好的改进效果。当k值取2时,对RCCNRS算法的性能提升是负值。ERC1和ERC2受k取值影响相对较大。当k取5时,取得最好的改进效果。ERC3受k取值影响较小,对于RCCNRS算法的分类性能提升基本稳定。随着k值增大,有少量提升。ERC3主要受原始算法分类精度影响。主动学习的过程中,被学习到的样本标签的准确程度取决于原始算法的分类精度。所以,如果原始算法分类精度高,ERC3对性能提升相对更有效。 4个数据集上的实验结果显示,当k取2时,3种策略对RCCNRS算法的性能没有提升,反而有下降。这是当k取2时,交叉验证的优势尚未体现。并且在交叉验证时,子训练集是原始训练集的一半,即不仅没有通过集成消除分类偏好还减少了训练样本。此时子训练集对应分类器的精度下降幅度大,大于交叉验证3种策略对原始算法分类精度的提升幅度。 各个数据集在不同数据切割比例下的实验结果分别如表2和表3。表2和表3中,同一训练集规模下,分类精度最高的结果由下划线标出。 表2 实验结果(Ⅰ) 表3 实验结果(Ⅱ) 从实验结果来看,由于训练集分割存在随机性,每次实验结果不一定完全相同,但3种改进策略,对RCCNRS算法分类精度都有一定的提升。其中,ERC1相对表现更好,但是当RCCNRS原本分类精度就比较高时,ERC3表现更好。比如ERC3在Mushroom和Voting数据集上,分类精度提升较另外2个数据集上效果更好。 在实验所用数据集上,和RCCNRS相比ERC1在4个数据集上的平均提升为0.72%,其中,在Chess和Kr-vs-kp数据集上分类精度提升更明显,分别是1.15%和1.20%;ERC2在4个数据集上平均提升为0.71%,在Chess和Kr-vs-kp数据集上的平均提升明显,分别为1.44%和1.60%;ERC3平均提升0.30%,同样,在Chess和Kr-vs-kp数据集上平均提升较明显,分别为0.58%和0.69%。对于Mushroom和Voting这2个数据集,因为RCCNRS算法原本分类精度较高,所以提升幅度较小。其中,ERC1和ERC2在Mushroom上平均提升较少,都为0.25%。ERC3在Voting数据集上提升最少,平均提升为0.18%。 在实验所用4个数据集上,ERC1对分类精度提升更明显;其次是ERC2和ERC1的分类精度相差不大;ERC3在Mushroom数据集上表现良好,即使RCCNRS算法分类精度达到98%时,也能对原始算法精度提升约0.5个百分点。 总体来说,本文提出的3种改进策略,对于RCCNRS算法分类精度较低的数据集,适宜采用ERC1和ERC2中的一种进行改进。对于RCCNRS原本分类精度就较高的数据集,宜采用ERC3对算法进行改进。根据本文实验数据,分类精度较高的标准应超过90%。ERC1和ERC2分类精度相差不大,优先考虑选择ERC1。对于大数据集,不过分要求精度的时候,建议ERC2。因为ERC2中,QBC中基分类器更少,算法复杂度更低。所以对于不同数据集,应该选择其相适应的改进策略。 针对RCCNRS算法分类精度受训练数据类别不平衡影响的问题,本文提出3种改进策略。总体来说,通过实验验证和分析得出如下结论:①对于RCCNRS算法,本文提出的3种k-fold交叉验证策略,当k取5时往往取得较好的分类性能提升。另外,ERC1和ERC2受k取值影响较大;ERC3受其影响较小,且ERC3随k值增加改进效果有微弱的提升;②对于RCCNRS算法分类精度较高的数据集,应选择ERC3。根据本文实验结果,分类精度应高于90%。对于RCCNRS原本分类精度低的数据集,应选择ERC1和ERC2中的一种。 本文提出的3种交叉验证策略,对RCCNRS的分类精度有一定的提升。3种交叉验证策略,同样可以用来研究其他的经典分类算法。其中,ERC3也可以研究数据集中特殊样本的选择和删除。在接下来的工作中,将结合属性加权[11]、三支决策[12-13]等对ERC3做进一步研究,研究ERC3如何有效筛选特殊样本。1.3 集成学习
1.4 主动学习
2 策略描述
2.1 集成策略1

2.2 集成策略2

2.3 集成策略3


3 实验及结果分析

3.1 k-fold对比

3.2 ERC与RCCNRS对比
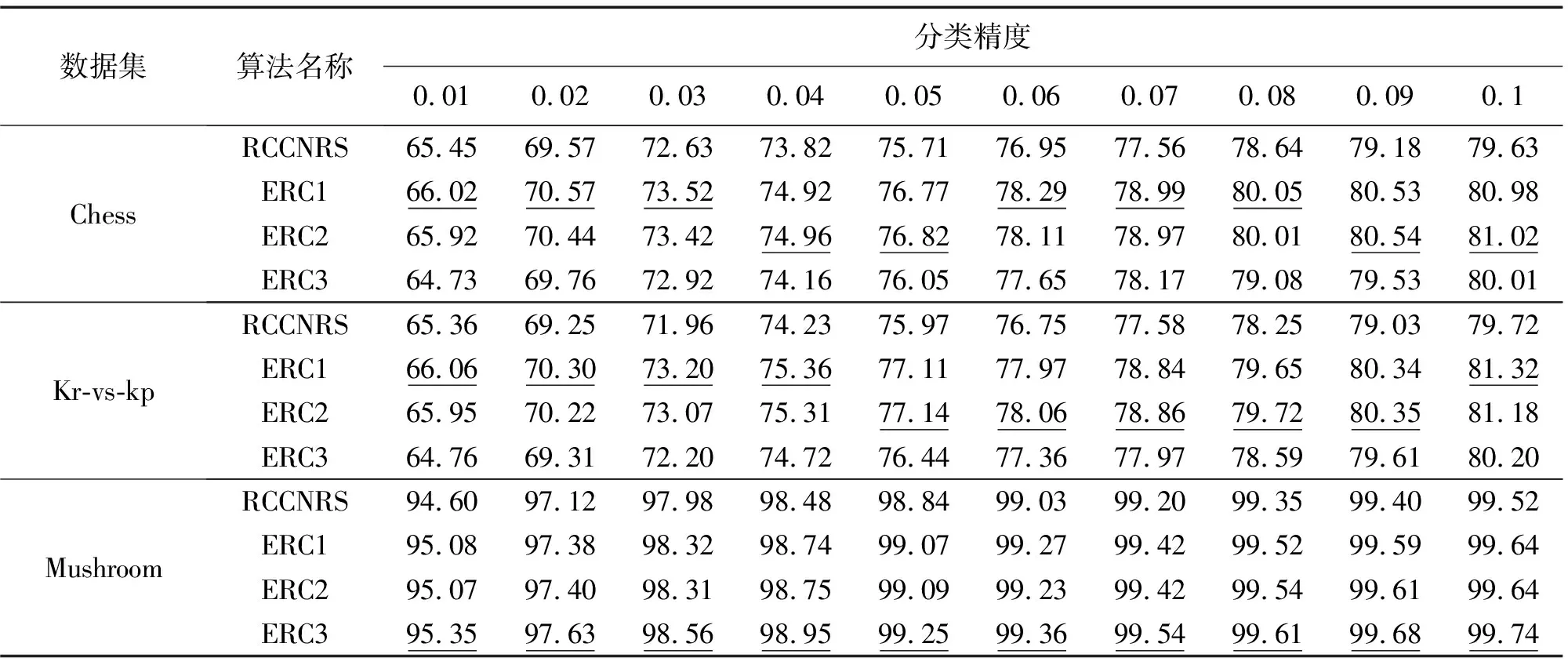
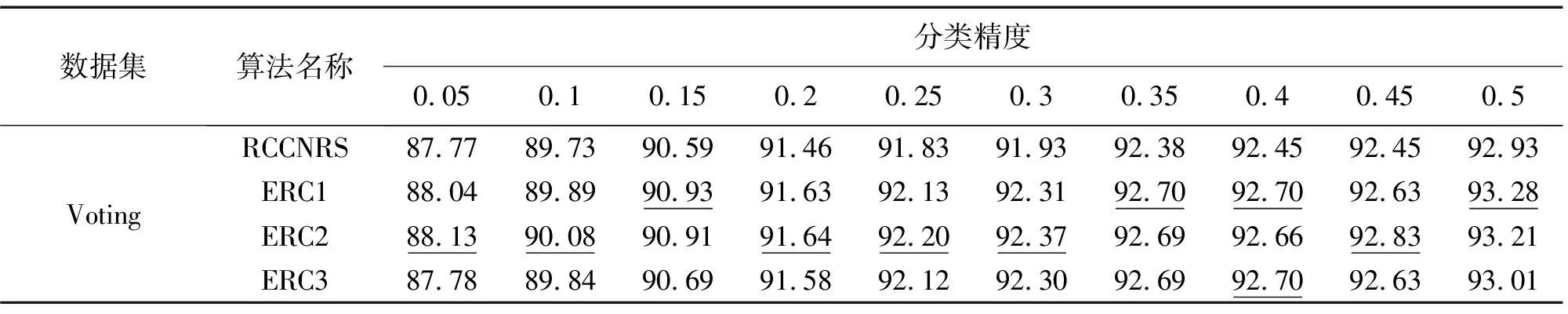
3.3 小 结
4 结论及进一步工作

