基于样本和特征搜索空间不断缩小的模糊粗糙集特征选择

杨燕燕，张 晓，李翔宇，杜晨曦，李懿恒

(1.北京交通大学 软件学院，北京 100044；2.西安理工大学 理学院，西安 710048)

0 引 言

随着信息与通信技术的迅猛发展，人们收集、存储、传输和管理数据的能力日益提高，使得各行各业积累了大量高维、海量数据[1]。这些高维海量数据中往往存在大量的冗余特征，这不仅增加了计算机的存储成本，还对传统机器学习算法的性能和效率带来了严峻挑战。特征选择[2-3]是机器学习和数据挖掘中处理高维数据的主流技术之一，其主要操作是通过特定的特征估计度量和搜索策略，移除冗余以及不相关的特征为构建好的预测模型选择一个紧凑的、有信息量的特征子集[4-6]。理论和实践表明，在执行分类任务之前，对高维数据进行特征选择可有效提高学习算法的可解释性、缩短学习算法的训练时间，并通过降低过拟合来提高学习算法的泛化性能[7]。目前，特征选择已经成为机器学习和数据挖掘领域中的一个研究热点，引起了学术界和企业界的广泛关注，并已成功应用于图像识别[8]、图像检索[9]、文本挖掘[10]、生物数据分析[11]、故障诊断[12]等众多应用领域。

模糊粗糙集[13-14]通过模糊信息粒化的方式为特征选择提供了一种有效的方法[15-16]。作为经典粗糙集模型[17]的推广，它是一种处理数值集中样本之间的不可辨识性和模糊性的有力数学工具。模糊粗糙集利用模糊相似关系来描述样本之间的相似性，刻画了数值数据中条件属性(特征)与决策标签之间的不一致性。这种不一致性表现为2个样本具有相同或相似的条件属性取值，却有不同的决策标签，其可通过模糊粗糙集的下近似对每个样本关于其决策标签指派一个隶属度来进行度量[18]。通过保持每个样本的这一隶属度不变，模糊粗糙集特征选择，也叫属性约简，就能删去冗余或者不相关的条件特征以获取一个有信息量的特征子集。

近年来，模糊粗糙集特征选择的研究已经取得了丰硕的成果，出现了各种各样的模糊粗糙集特征选择算法[19-23]。这些算法可分为基于测度的启发式算法和基于区分能力的结构化方法。其中，基于区分能力的结构化方法以辨识矩阵的方法为典型代表，从样本之间的区分能力的角度构造了属性约简方法。模糊粗糙集辨识矩阵的思想首次由文献[15]引入，其利用辨识矩阵的方法研究了属性约简的本质，设计了计算一个约简的辨识矩阵算法。然而，该辨识矩阵的方法需要占据大量的内存，并不适用于大规模数据。鉴于此，文献[24]提出了基于极小元素的模糊粗糙集特征选择算法，该算法极大减少了运行时间同时节省了大量的内存空间。利用文献[24]中的相对辨识关系的定义，文献[25-26]构造了基于相对辨识关系的模糊粗糙集特征选择算法。

基于测度的启发式算法主要借助前向搜索的方式，通过保持数据集的模糊依赖函数或模糊信息熵等特征估计测度不变来获取该数据集的最优特征子集。比如，最早提出模糊粗糙集属性约简概念的文献[27]将经典粗糙集中保持依赖函数不变的思想平移到模糊粗糙集的框架中，设计了一个模糊粗糙集特征选择的快速算法。然而，文献[15]指出，文献[27]所提算法是不收敛的，这对特征选择的执行带来了诸多问题。文献[28-29]用模糊熵的概念刻画了特征的重要性，进而提出了基于模糊熵的特征选择算法。通过改进文献[28]中模糊条件熵的定义，文献[30]定义了λ-条件熵，并提出了基于该模糊熵的filter-wrapper算法。文献[31]在所提出的拟合模糊粗糙集模型下定义了模糊依赖函数，并设计了一个拟合模糊粗糙集特征选择的前向启发式算法。文献[32]定义了特征子集的邻域区分索引，基于此度量设计了一个数值数据的特征选择算法。文献[33]定义了模糊粗糙集自信息，并设计了一个基于模糊自信息的特征选择算法。

上述2类模糊粗糙集特征选择算法不仅具有丰富的理论，也在实践中表现出了良好的性能。但是，在确定每一个最优候选特征的过程中，它们都需要遍历数据集的所有样本来计算每个候选特征加入后的特征估计测度，如依赖函数、信息熵等。事实上，并不需要借助数据集的所有样本来确定一个最佳候选特征，这便需要借助样本筛选策略，文献[34-35]已经研究过样本筛选的机制，但是它们却致力于增量特征选择算法，这不是本文的研究范畴。另外，在每次迭代过程中，上述算法也都需要遍历所有剩余的候选特征来确定一个最佳候选特征。事实上，有些候选特征可能是冗余的，对特征选择过程不起任何作用。通过这2方面的分析，上述2类模糊粗糙集特征选择算法还不够高效。基于这2个动机，本文通过研究样本筛选机制和特征搜索准则，在每次确定一个最佳候选特征后，缩小样本和特征的搜索范围，构造一个新的模糊粗糙集特征选择算法。在UCI机器学习数据集上的实验结果也表明该算法的有效性和时间高效性。

1 基于依赖函数的模糊粗糙集特征选择

本节简要介绍基于TM-相似关系的模糊粗糙集模型、正域、依赖函数及其特征选择等相关概念。

1.1 模糊粗糙集

设U是一个非空论域，F(U×U)是U×U上的模糊幂集。R∈F(U×U)是U×U上的模糊二元关系。如果对任意x,y,z∈U，R是自反、对称、TM传递的，则称R是U上的一个模糊等价关系。

文献[13]首次定义了如下模糊粗糙集的概念。

定义1[13]设U是非空论域，R是U上的一个模糊等价关系，X∈F(U)。对任意x∈U，X的模糊下、上近似算子分别定义为

基于上述模糊粗糙集，学者们构造了几类广义模糊粗糙集模型，有兴趣的学者可参阅文献[36-37]。本文的研究工作是在定义1的基础上展开的。

1.2 模糊粗糙集特征选择

本文用模糊决策表(U,A∪D)来表示一个数值或者混合数据集，其中U={x1,…,xn}是数据集中所有样本的集合，A是数据集中描述样本的所有特征构成的集合，D={d}是决策特征的集合，用于确定数据中样本的标签或者类别。因此，U中的每个样本x可由特征集合A描述，d(x)是样本x的标签。

性质1[38]设(U,A∪D)是模糊决策表，B⊆A。任意x∈U对其自身决策类[x]D的下、上近似隶属度可简化为

样本x属于其自身决策类下近似的隶属度取值为[0,1]，它与x属于模糊正域的隶属度之间有下列关系。

样本x属于B的模糊正域的隶属度实质上是x对其自身决策类下近似的隶属度。

依赖函数取值于[0,1]，它的几何含义可解释为论域中所有样本到其异类样本最小距离的平均。模糊依赖函数也表明特征子集B对决策的拟合程度。

定义4[28,39]设(U,A∪D)是模糊决策表，P⊆A是决策表的一个约简或最优特征子集，若它满足：

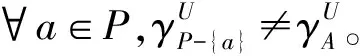
定义4中的条件1)表明约简能保持决策表的依赖函数；条件2)表明约简是保持决策表依赖函数不变的极小特征子集，即从约简中删去任何一个特征都不能保持决策表的依赖函数不变。

性质2[39]设(U,A∪D)是模糊决策表，B⊆C⊆A，则有

性质2表明随着特征集合的增加，模糊决策表的正域和依赖函数单调递增。这一结论是构造特征选择算法的理论基础。文献[39-40]，已经给出基于模糊依赖函数的特征选择算法的具体形式，为了便于实验比较，本文重新阐述基于依赖函数的模糊粗糙集特征选择算法(用DFFS表示)。该算法从空集开始，逐步选择一个使得依赖函数增加最大的候选特征，并将其加入当前所选特征子集中，直至数据集的模糊依赖函数保持不变。该算法的伪代码如下。

算法1DFFS算法

输入：决策表(U,A∪D)。

输出：约简P。

For eachai∈A-P

End for

End while

④输出约简P并终止算法。

在每次迭代过程中，该算法的步骤③都需遍历数据集的所有样本来计算每个可能的候选特征加入后的依赖函数，进而从所有剩余候选特征中确定一个最佳特征。这种搜索模式必须借助于数据集的所有样本和当前所有剩余特征。当处理海量高维数据时，这种搜索模式常常需要花费大量运行时间。因此，为节省计算模糊粗糙集特征选择的计算成本，本文进行了深入研究。

2 基于样本和特征搜索空间不断缩减的模糊粗糙集特征选择算法

本节提出了一种基于样本和特征搜索空间不断缩减的模糊粗糙集特征选择算法(用SSFFS表示该算法)。首先，基于性质2中样本对其自身决策类下近似隶属度单调递增的特性，构造样本筛选机制，用以筛除决策类下近似已被当前所选特征子集保持的样本，这些样本将不参与后续特征选择过程中依赖函数的计算。其次，定义特征冗余性的概念，设计特征搜索准则，用以移除已被判定为冗余的特征，在后续特征选择的过程中将不再搜索这些特征。最后，通过融合样本筛选机制和特征搜索准则，相应的模糊粗糙集特征选择算法得以设计。

根据性质2，有下列结论。

该定理表明，若当前所选特征子集B能保持样本x对其自身决策类下近似的隶属度，则在特征选择的后续过程中，可不用再计算该样本对正域的隶属度，这样的操作可节省样本空间的搜索范围。于是，就有了样本筛选机制。

定义5表明，若加入候选特征a到B不能使依赖函数增加，则a相对于B是冗余的。

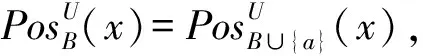
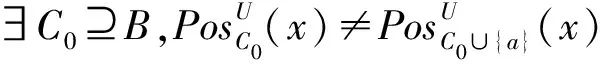
类似上述的推导，有

该引理表明在特征选择过程中，若一个候选特征的加入不增加样本的正域，则在后续特征选择过程中，该候选特征的加入依然不增加该样本的正域。

定理2对于a∈A-B，若a关于特征子集B是冗余的，则对任意C⊇B，a关于特征子集C也是冗余的。

该定理表明，在特征选择的早期过程，已经被判定为冗余的特征在后续特征选择的过程中仍然是冗余的。因此，在特征选择的过程中，可不搜索这些冗余特征，从而能节省特征选择的运行时间。基于定理2，本文给出如下特征搜索准则。

通过上述样本筛选机制和特征搜索准则，本文设计了基于样本和特征空间搜索范围不断缩减的模糊粗糙集特征选择算法，简记作SSFFS算法。

算法的思路如下：从空集P开始，将剩余特征集合left中的每个特征加入P中，计算每个候选特征加入后的依赖函数；将依赖函数增加最多的特征选作最佳的候选特征，并将其放入P中；计算最佳候选特征加入后的冗余样本集合fs(P)和冗余特征集合rf(P)；在确定下一个最佳特征时，只需计算剩余候选特征集合A-P-rf(P)(而不是A-P)中每个特征加入后，U-fs(P)(而不是U中每个样本的正域)中每个样本的正域。通过重复上述步骤，当剩余样本的个数为0或者剩余特征个数为0，算法就终止，从而得出数据集的一个约简。

具体算法如算法2。

算法2SSFFS算法

输入：决策表(U,A∪D)。

输出：约简P。

//*集合S是筛除冗余样本后所剩样本的集合；集合left是删去冗余特征和最佳候选特征后所剩特征的集合。*/

③WhileS≠φandleft≠φdo

For eachai∈left

For eachxj∈S

//*计算集合S中每个样本的正域*/

End for

End for

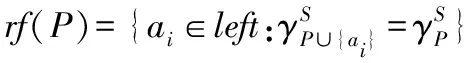
End while

④输出约简P并终止算法。

算法2能快速计算一个数据集的约简。步骤②与算法1的步骤②一样，都是计算U中每个样本的正域，并计算依赖函数，其复杂度为O(|U|2|A|)。步骤③每次将已删去冗余特征后的特征集合left中每个特征加入P，计算筛除冗余样本后的集合S中每个样本的正域，进而确定一个最佳候选特征，这种方式可有效缩减样本和特征空间的搜索范围，其复杂度为O(|left|(|P|+1)|S||U|)。而算法1中步骤②的复杂度为O(|A-P|(|P|+1)|U||U|)。显然，|S|<|U|，|left|<|A-P|，故O(|left|(|P|+1)·|S||U|)

3 实验结果与分析

为了验证本文所提出的SSFFS算法的有效性和时间高效性，本节在8个UCI数据集上比较SSFFS算法与DFFS算法、RDRAR算法[25]、HANDI算法[32]。下面给出具体的实验设置与结果分析。

3.1 实验设置

实验所用的具体运行环境配置如下：Intel(R)Core(TM)i7-7700 CPU @ 3.60GHz 3.60GHz(2 processors), 64.0GB。运行的软件环境为：Matlab R2018b。实验选取的8个数据集均来源于UCI机器学习数据库(1)http://archive.ics.uci.edu/ml/index.php，详见表1。

表1 实验数据集

对表1中的每个数据集，采用十折交叉验证法得到实验结果。具体地，所有样本被均分为10份，每份轮流作为测试集，剩下的9份作为训练集。对任意一个训练集中的特征，定义一个模糊等价关系Ra(xi,xj)=1-|a(xi)-a(xj)|，其中，xi和xj是该训练集中的样本。

在每个训练数据集上，使用特征选择算法得到相应的最有特征子集。在约简后的训练集上使用Matlab自带的KNN训练分类器，其中分类器的参数均为默认设置。将训练好的分类器作用于约简后的测试集，得到相应的分类精度。这个过程对每一对训练集和测试集都执行一次，因而最终报告的实验结果是10次实验结果的平均值。

本实验将比较如下指标。

2)所选特征个数。每个特征选择算法在10个训练数据集上所选特征的平均个数。

3)分类精度。KNN分类器在约简后的测试数据集上的平均分类精度。

3.2 实验结果

首先给出SSFFS算法、DFFS算法、HANDI算法和RDRAR算法在每个数据集上的平均运行时间、所选特征个数、平均KNN分类精度；接着，证实SSFFS算法确实在特征选择的每次迭代过程中都能删去冗余的样本和冗余的特征，从而说明它确实在几乎每次迭代时都能减少样本和特征的搜索空间。

表2列出了4个算法SSFFS、DFFS、HANDI和RDRAR在每个数据集上的平均运行时间，即每个特征选择算法在每个数据集对应的10个训练数据子集上的平均运行时间。从表2可以看出，在每个所选数据集上，SSFFS算法都比DFFS算法、HANDI算法和RDRAR算法快。具体地，在数据集Anneal上，SSFFS算法的运行时间分别是DFFS算法的运行时间的7.198 3%、HANDI算法的24.15%、RDRAR算法的31.19%。在高维数据集Gearbox上，SSFFS算法的运行时间仅是DFFS算法的运行时间的2.4%、HANDI算法的10.71%、RDRAR算法的28.74%。在大规模数据集Thyroid上，SSFFS算法的运行时间下降至DFFS算法的3.8%、HANDI算法的7.91%、RDRAR算法的4.26%。这些事实表明，与DFFS算法、HANDI算法和RDRAR算法相比，SSFFS算法可在最短的时间内获取一个最佳特征子集。其主要原因在于，所提SSFFS算法的核心在于能在每次迭代的过程中缩小样本空间和特征空间的搜索范围，这种双向缩小范围的搜索模式可极大提高特征选择的计算效率。

表2 不同特征选择算法的运行时间

表3列出了4个特征选择算法在每个数据集上所选特征的个数，其中Raw data表示原始数据集中特征的个数。从表3可看出，所提SSFFS算法在8个数据集上所选特征的平均个数仅为8，明显小于原始数据集的平均特征个数39.6。SSFFS算法所选特征的平均个数也小于算法HANDI算法(平均个数为8.7)、DFFS算法(平均个数为26.4)以及RDRAR(平均个数为33.8)。这些实验结果表明，所提SSFFS算法能删去更多冗余特征。为了说明SSFFS算法对分类器性能的有效性，表4列出了每个数据集的KNN预测精度，其中Raw是KNN分类器在原始数据集上的分类精度。从表4可看出，SSFFS算法具有最高的平均分类精度0.908，其次是RDRAR算法的分类精度0.906 6，接着是DFFS算法的分类精度0.905 4，最后是HANDI算法的分类精度0.889 7。它们都比原始数据集的平均分类精度高(为0.874 8)。这一结果说明特征选择确实可以改进学习算法的性能。

表3 不同特征选择算法的所选特征的个数

表4 不同特征选择算法的KNN平均分类精度

表2—表4表明，本文所提SSFFS算法不仅能快速地从数据集中选择最有特征子集，也能有效减少冗余特征并能改善学习算法的分类性能。

图1给出了SSFFS算法在每次迭代的时候，删去冗余样本和冗余特征的个数。从图1能看出，SSFFS算法几乎在每次迭代时都能移除冗余样本和特征。比如在数据集Anneal上，一共执行了4次迭代，每次迭代时分别移除了7，24，3，0个特征，同时每次迭代时分别移除了108，90，63，85个样本。在数据集Park上，一共执行了2次迭代，第1次迭代时移除了2个特征，324个样本，第2次迭代时移除了24个特征，298个样本。在大规模数据集Thyroid上，SSFFS算法一共执行2次循环，第1次循环时删去了20个特征和28个样本，第2次循环时删去了7个特征和880个样本。这些结果证实，所提SSFFS算法确实在几乎每次迭代过程中都能移除冗余样本和冗余特征，能有效地减少样本和特征的搜索范围，从而极大地提高了特征选择的计算效率。

图1 每次迭代时SSFFS算法移除样本和特征的个数

4 结 论

本文提出了一种基于样本和特征空间搜索范围不断缩减的模糊粗糙集特征选择算法，该算法的核心思想是样本筛选机制和特征搜索准则的构造。具体地，本文首先利用每个样本的正域随特征单调递增的性质，构造了样本筛选机制，用以筛去正域已能被当前所选特征子集保持的样本。其次，本文采用特征冗余的概念，构造了特征搜索准则，用以删去不能使当前所选特征子集依赖函数增加的特征。接着，将样本筛选机制和特征搜索准则相融合，提出了SSFFS算法。实验结果表明SSFFS算法的有效性和高效性，SSFFS算法在每次迭代的过程中都能有效减少样本和特征的搜索范围。

本文的研究工作在基于TM-模糊粗糙集模型的基础上展开的，下一步可以在广义模糊粗糙集模型上作进一步验证和研究。具体如下：①将本文的研究思想推广至广义粗糙集模型，构建广义粗糙集模型特征选择的快速算法；②本文的研究集中于数值数据集或者混合数据集的处理，并未涉及更复杂的数据集，诸如缺失数据、集合值数据、文本数据、图片数据等，因此，后续研究也可以把本文的核心思想用于处理更加复杂的数据集，从而建立新的特征选择快速算法；③特征选择算法的稳定性并未涉及，未来对其展开研究，将形成特征选择稳定性的丰富理论。