拓扑绝缘体量子点中的磁交换相互作用

尹柱财，李 健，朱家骥

(重庆邮电大学 理学院，重庆 400065)

0 引 言

随着现代半导体工艺的发展，人工制备量子限制结构的技术逐渐成熟。半导体量子点作为一种零维的纳米结构，在过去的三十多年里受到了人们的广泛关注[1-4]。具有零维特性的量子点常被称为人工原子，量子点中电子的运动在3个方向受到限制，当特征尺寸与电子的费米波长可比拟时，人们可以利用多种调节手段对量子点系统的光学性质、输运性质和磁性进行调控。这使得量子点不仅是基础研究的重要对象——可以利用量子点实现普通原子所无法或不易实现的物理现象，同时也是各种应用技术的平台——诸如实现半导体自旋电子学器件、量子计算机基础元件以及光电器件等。[5-7]

由于量子点具有库仑阻塞特性，人们可以很方便地将1个或2个电子限制在单量子点或双量子点中。电子的自旋可以视为量子比特，只要能够发展有效调控量子点自旋或磁性的手段，并保持电子自旋的相干特性，就能够实现自旋电子学或量子计算的应用。人们已经在常规半导体量子点上通过实验实现了对自旋或磁性的电场、磁场或者磁掺杂调控[8-16]。

与常规半导体量子点相比，拓扑绝缘体量子点在其导带与价带带隙之间的量子态成环形分布在量子点的边界处。这些环形边缘态能量是等间隔分布的，能量间隔仅依赖于量子点的周长。量子点中的环形边缘态是自旋极化的并且具有自旋轨道锁定的特性，边缘态之间禁止光学跃迁，从而导致光学暗态的出现。光学暗态在量子信息储存方面有积极的应用前景[17]。此外，人们还可以利用环形边缘态制备极化的太赫兹光和纠缠光子对[18]，这使得拓扑绝缘体量子点成为一种有希望的量子通信基本元器件。

在常规半导体量子点中，不同的壳层结构与电子几率密度分布决定磁离子和电子的相互作用强度，进而影响磁性。量子点的壳层结构依赖于量子点的大小和约束势的对称性。常见的限制势有：①圆盘型限制势，一般取为(1/2)m*ω2(x2+y2)，对应的壳层结构为(2,6,12,20,…)[19-22]，即基态可以容纳2个电子，第一激发态可以容纳4个电子，更高的激发态以此类推；②椭圆型限制势(ωx/ωy=2)，相应的电子壳层结构为(2,4,8,12,18,…)[23]；③三角型限制势，相应的电子壳层结构为(3,6,9,…)[24]。以常规圆盘型量子点为例，电子和Mn离子的相互作用强烈依赖于量子点中电子的数目，满壳层时Mn离子和电子的相互作用消失，部分填充时Mn离子和电子的相互作用最强[16]。量子点中存在2个Mn离子时，Mn离子和电子的相互作用在不同电子填充下会对量子点的磁性产生不同的影响。当部分填充时，多电子的极化效应会导致Mn-Mn的铁磁相互作用；满壳层时，2个Mn离子以传导电子作为媒介产生间接交换关联，由于电子和Mn离子的sp-d交换相互作用在自旋平行时取最小值，因此在加入第一个Mn离子时，会引起电子的弗雷戴尔振荡，使得电子自旋随着与Mn离子间距的增大与Mn离子自旋平行或反平行排列。当再增加一个Mn离子时，就会导致新加入的Mn离子自旋与其最近邻的电子自旋平行排列，相应于与第一个Mn离子平行或反平行排列，表现为铁磁或反铁磁相互作用。这种磁性产生机制就是所谓的RKKY(Ruderman-Kittel-Kasuya-Yosid)相互作用[25-27]。量子点中的RKKY相互作用通常还依赖于电子填满多少个壳层[28]。

上面讨论了圆形、椭圆形、矩形等各种形状拓扑绝缘体量子点的电子结构、壳层结构及其调控[29-31]。与常规半导体类似，拓扑绝缘体量子点同样具有壳层结构，但拓扑绝缘体量子点的壳层结构与常规半导体量子点的壳层结构显著不同。由于量子点的磁性依赖于壳层结构，因此，预期拓扑绝缘体量子点的磁性与常规半导体量子点相比会有一些独特的性质。

为了澄清拓扑绝缘体量子点的磁性，本文基于构型相互作用方法对HgTe拓扑绝缘体量子点中磁离子和电子的交换相互作用以及2个磁离子间通过巡游电子为中介的RKKY相互作用进行了计算。发现电子和单个Mn离子的相互作用强烈依赖于量子点中电子的数目，对于偶数电子，满壳层时相互作用为零，该相互作用可以通过量子点中化学势改变的奇偶振荡行为进行测量。对于量子点中包含2个磁性离子的情形，满壳层时计算表明2个磁离子之间的交换相互作用为RKKY相互作用，即Mn离子以边缘态中的巡游电子为中介的间接交换关联。

1 计算方法

图1 刻蚀得到的拓扑绝缘体量子点结构示意图

(1)

(2)

量子点中包含少数个电子和2个Mn离子的哈密顿量为

(3)

(3)式中：前三项为Mn离子的子系统，包含电子和Mn离子的相互作用、Mn离子之间的相互作用，其中，J12为磁离子间交换相互作用强度；第四项表示单电子的动能；Ei,σ为自旋为σ的单电子在轨道|i〉上的能量，即无相互作用项；第五项中〈i,j|Vee|k,l〉是将电子从|kσ′,lσ〉态散射到|iσ,jσ′〉态的散射矩阵元，即库仑相互作用项

(4)

(5)

(5)式中，s-d交换常数Jsd=-27 meV·nm2，p-d交换常数Jpd=54 meV·nm2，见文献[36]。

本文采用构型相互作用方法数值求解少数个电子的哈密顿量He为

(6)

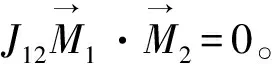
(7)

N电子和单个磁性离子本征态的计算选用如下的构型，即

(8)

N电子和2个磁性离子本征态选用如下的构型，即

(9)

2 结果与分析

本文首先给出了半径为50 nm的碲化汞(HgTe)拓扑绝缘体量子点的能谱和边缘态电子的几率密度分布，其圆盘型拓扑绝缘体量子点的电子结构如图2。如图2a可以看出，体内态(黑色实心圆点)能隙之间存在边缘态(红色和蓝色空心圆圈)。边缘态的能量是二重简并的，由自旋向上和自旋向下的电子构成，并且能级是等间隔分布的。对于边缘态，自旋向上和自旋向下的电子主要分布在量子点的边缘上，因此，当研究边缘态电子和Mn离子的相互作用时，本文仅考虑将Mn离子放置在量子点的边缘附近的几何构形。

图2 圆盘型拓扑绝缘体量子点的电子结构

在量子点中加入Mn离子在实验上可以通过空间分辨的原子力显微镜实现。本文首先考虑在量子点的边缘态处(R,0)增加一个Mn离子。通过计算包含有Mn离子和N电子基态的能量与仅包含N电子基态能量的差值可以间接计算Mn离子和电子的sp-d交换相互作用强度Δ(N)=|Ec-Ee|，如图3a所示。当选取有限基矢空间时，构型空间选取的电子个数与计算的电子个数相同，计算的能量差值清楚地显示了一个奇偶振荡。当N为偶数时，能量差值会消失，这是因为偶数电子基态总自旋为零，没有净电子自旋；当N为奇数时，能量差值总是负的，这是由于奇数电子的净电子自旋为1/2，与磁性离子之间的交换相互作用总是使得系统的总能量降低，因而可以推测电子和Mn离子之间为反铁磁相互作用。内插图为构型空间选取的电子个数为10个单粒子态，是更精确的构型计算结果——同样也表现出奇偶数的振荡行为。

电子和单个Mn离子的相互作用可以通过电容谱或者库仑阻塞谱进行测量。这2种测量方法均需要测量量子点中化学势的改变，即测量增加一个电子时系统总能量的改变，μ(N)=E(N)-E(N-1)。掺杂前后的化学势变化可用Δμ=μc-μe表示。Mn离子对于N电子量子点化学势的影响可以通过掺Mn离子与未掺Mn离子的化学势改变观察到，如图3b所示。可见当电子数N为奇数时会有一个负位移，而当电子数N为偶数时会出现一个正位移。

图3 量子点中加入单个Mn离子时的计算结果

接着讨论满壳层时Mn-Mn以电子作为媒介的间接交换相互作用。该相互作用的强度可以由Δ=Ec-Ee给出，Ec是包含2个Mn离子和N个电子时量子点的基态能；Ee为仅包含N个电子时量子点的基态能。对于偶数电子的情形，图4的康拓图为构型相互作用计算的结果，计算中考虑了电子之间的相互作用，结果表明，当将一个Mn离子放于量子点边缘位置(R,0)时，再往量子点中放入一个Mn离子时，该相互作用强度随第二个Mn离子的位置改变而改变，即当2个Mn离子比较近时为铁磁相互作用，当2个Mn离子之间距离变大时变为反铁磁相互作用。对比图4a和图4b，发现Mn离子间的相互作用还和满壳层量子点中电子的具体个数相关。

对于边缘态包含偶数电子的情形，电子构成闭合壳层，电子基态的总自旋为零，因而电子自旋与Mn离子自旋没有直接的相互作用，但电子中介了不同磁离子从而导致间接的RKKY相互作用。对于量子点中包含2个磁离子的情形，可以通过二阶微扰理论来计算RKKY相互作用：2个Mn离子的相互作用可以表示为

(10)

图4 拓扑绝缘体量子点中2个Mn离子的相互作用强度(插图为考虑了电子-电子相互作用的情形)

3 结 论

本文基于构型相互作用方法研究了HgTe拓扑绝缘体量子点中电子与Mn离子的相互作用以及两个Mn离子间通过拓扑边缘态巡游电子为中介的间接交换相互作用。拓扑绝缘体量子点的壳层结构是二重简并的，其电子分布于量子点的边缘处，电子与Mn离子的sp-d相互作用会出现奇偶振荡行为。量子点中加入2个Mn离子时，Mn离子间的相互作用取决于Mn离子间距和量子点壳层中电子的个数。本文的研究澄清了拓扑绝缘体量子点壳层结构对其磁性的影响，有助于设计基于拓扑绝缘体量子点的自旋或量子器件。