单电感双输出Boost变换器的目标全息反馈非线性控制
李畸勇,潘恒宇,刘斌,谢敏
(1.广西大学 电气工程学院, 广西 南宁 530004;2.西南交通大学 工程训练中心, 四川 成都 610031)
0 引言
近年来,随着平板电脑及一些小型便携式设备的快速发展,其内部模块增多且结构复杂。这些设备内部的不同模块往往需要不同电压等级的电源供电[1]。比如在计算机里的显卡,内存条,硬盘等,它们所需要的供电电压是不同的,分别是12 V、3.3 V和5 V。如果为不同的模块设计独立电源供电会导致电子设备损耗变大,产生拍频干扰,尺寸增加等问题[2-3]。
为了解决这些问题,人们提出了单电感多输出开关变换器(single-inductor multiple-output,SIMO)拓扑[4]。该变换器只需要一个电感就可以输出多路电压,极大地节约了设备的空间,有利于笔记本电脑和一些便携式设备的小型化。因此,SIMO变换器凭借其体积小,效率高,成本低等优点被人们广泛应用于各个领域[5- 6]。
但是,相比于传统的单电感单输出开关变换器,SIMO开关变换器是典型的多输入多输出非线性耦合系统,其拓扑结构更加复杂。SIMO开关变换器有着多个控制参数和多条输出支路,且所有的输出支路共用一个电感。当一个输出支路负载发生变化时,它从电感上获取的能量也会发生变化,这必将会影响其他支路的输出,产生交叉调节[7- 8]。当SIMO开关变换器发生轻微的交叉调节时,系统的输出精度会发生变化,当SIMO开关变换器发生严重的交叉调节时会导致整个系统的失稳。因此,如何抑制交叉调节成为SIMO开关变换器的一个重要研究课题[9-10]。
为了抑制SIMO开关变换器的交叉调节,研究人员提出了很多控制算法。早期人们针对断续导电模式(discontinuous conduction mode,DCM)下的单电感双输出Boost变换器提出了分时复用的技术[11]。通过该技术使得两个支路充电过程分离,从而减少交叉调节。但该方法使用的条件是变换器工作在DCM下,这会导致变换器的带载能力下降。文献[12]为解决文献[11]存在的问题,提出了伪连续导电模式下的单电感双输出(single-inductor dual-output,SIDO)Boost变换器的续流切换控制策略。该方法通过并联的续流二级管,可在每个支路各自充放电后将盈余的能量储存在电感中,这样系统的电流就不会下降至零,从而提高了带载能力。文献[13]提出了一种利用峰值电流和差模电压比较的控制方法,该方法在连续导电模式下,实现了SIDO buck变换器各输出支路的独立控制,具有较小的交叉调节。有学者认为输出电容的电流比电感电流更能反映负载的变化,因此提出一种电容电流-电容电压纹波控制技术[14]。该方法由于引入了更能直接反映负载变化的电容电流,而有更好抑制交叉调节的效果。上述文献所提出的方法在一定程度上抑制了SIMO开关变换器的交叉调节,但是大部分算法都是基于小信号模型的基础上提出来的,具有一定的局限性,因为小信号模型在平衡点处的线性化忽略了高阶非线性项。精确反馈线性化(exact feedback linearization,EFL)可以将非线性系统映射到线性系统,且转化过程没有忽略任何高阶非线性项[15-16]。有学者通过构建新的输出函数使其与系统的相对阶等于系统的维数,然后将EFL方法用于控制SIDO Boost变换器,实现了输出电压大范围下的稳定,极大的降低了交叉调节的影响[17]。然而构建新的输出函数需要求解偏微分方程,对于一些高阶系统,找到满足EFL条件的输出函数并不容易。文献[18]针对SIDO Boost 变换器提出一种输入-输出线性化技术,并指出SIDO Boost 变换器为非最小相位系统,需要将其先转化为最小相位系统才能使用该线性化技术,因为非最小相位系统具有不稳定的零动态。为了解决上述线性化方法存在的问题,文中提出采用目标全息反馈非线性控制方法对SIDO Boost变换器的控制器进行设计[19]。该过程中,只需系统状态目标量与系统具有一阶相对阶,即可建立控制量与状态目标量的联系,从而控制整个系统。无需构造复杂的输出函数来满足相对阶与维数相等的条件。同时文中还将证明通过该非线性反馈可以将系统的极点配置到稳定域。最后对所采用的控制策略和共模-差模电压控制策略进行了对比,验证了所研究控制策略的优越性和正确性。
1 SIDO Boost 变换器仿射非线性模型
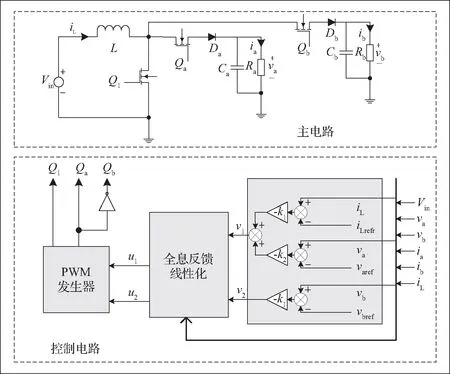
图1为SIDO Boost变换器的主电路图,该变换器有a、b两条支路,其中Vin是输入电压,L是共用的滤波电感,Ca和Cb分别是支路a、b的输出滤波电容,Ra和Rb分别是支路a、b的负载,va和vb是分支输出电压,ia和ib是分支输出电流,iL是滤波电感电流,Qa和Qb是分支开关器件,Da和Db是分支二极管。
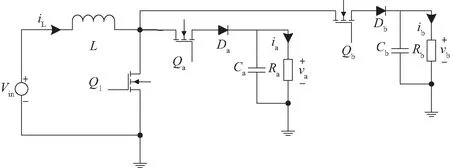
图1 SIDO Boost变换器主电路图
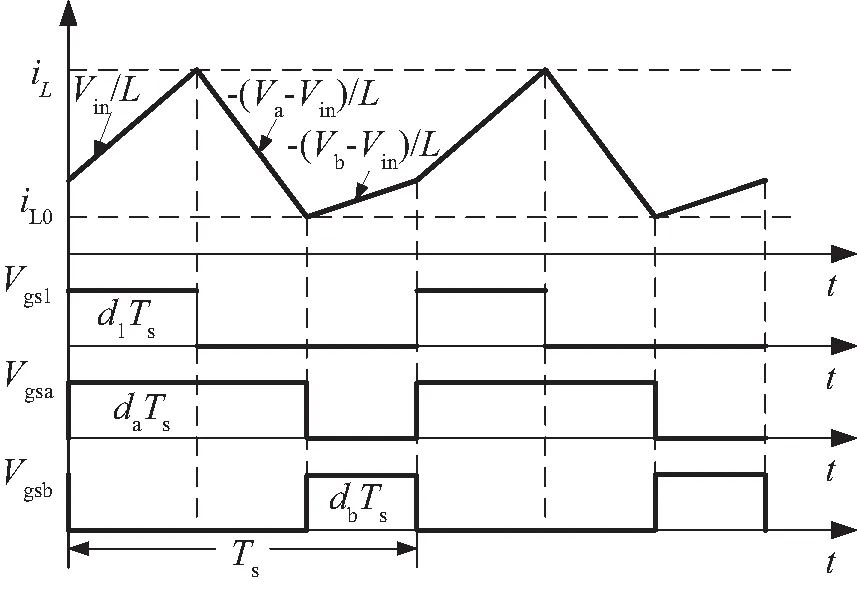
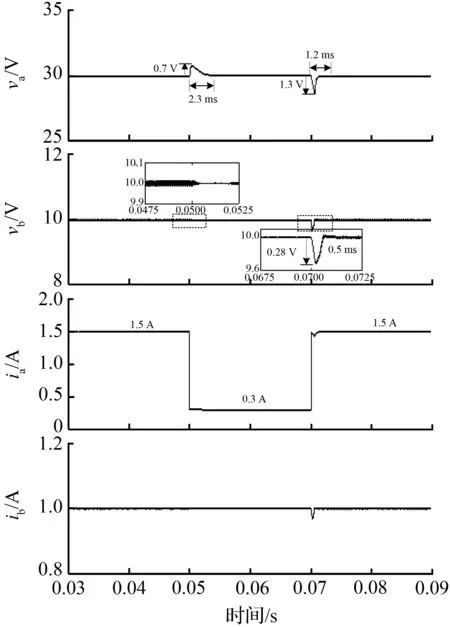
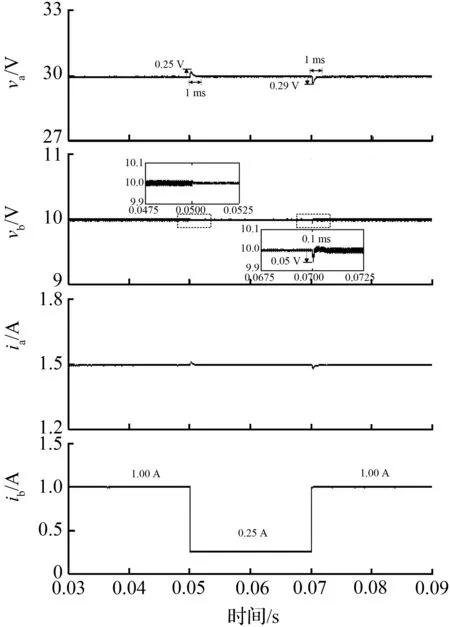
假设在两支路中先打开开关Qa,图2展示了双升压模式下SIDO Boost的稳态时序图,其中Va和Vb分别表示支路a、b的电压稳态值,Q1、Qa和Qb的控制信号分别是Vgs1、Vgsa和Vgsb,相应的开关占空比分别是d1、da和db,并且满足0 图2 双升压模式下CCM SIDO Boost变换器稳态时序图 (1) 其中, 由上状态方程可以看出g1(x)u1和g2(x)u2均为状态量和控制量的乘积,所以CCM SIDO Boost变换器可以看作是一个双输入双输出的非线性耦合系统。以往的研究主要是让SIDO Boost变换器工作在双升压模式,而SIDO Boost变换器工作在升降压模式的研究较少。因此文中主要研究SIDO Boost变换器工作在升降压模式下的控制响应。设输入电压到a支路输出电压的增益为Ma,到b支路输出电压的增益为Mb,有下式成立: (2) (3) 具体推导过程见文献[20],其中,Ra和Rb分别为支路a和支路b的电阻;Va和Vb分别为支路a和支路b输出电压的稳态值;da为图一中开关Qa的占空比;d1为图1中开关Q1的占空比。不妨假设支路a为升压模式,即Va>Vin,支路b为降压模式,即Vb (4) SIDO Boost变换器系统参数见表1,由于文中对电感电流纹波与输出电压纹波无过多要求,所以在保证电感电流连续情况下,表1参数参考文献[17]。将表1的参数代入式(4)中存在可行解,即变换器可以工作在一支路升压另一支路降压的模式,即有Va>Vin和Vb 表1 SIDO Boost变换器系统参数 图3 升压模式下支路a和降压模式下支路b的CCM SIDO升压变换器稳态时序图 在系统(1)中要求支路a的输出电压可以跟踪参考值varef,支路b的输出电压可以跟踪参考电压vbref,取系统(1)中的输出函数,可计算得: (5) e=y-yr, (6) 利用式(6)的多目标方程主动构建布鲁诺夫斯基标准型如下所示: (7) (8) (9) 式(8)与(9)是将系统状态量iL和vb与2个控制量u1和u2联系起来的关键,对于转换后的线性系统,按照线性最优原理选取如下的性能指标: (10) 可得线性控制量形如下式: (11) 式中,k1,k2,k3为反馈系数,由式(8),(9),(11)得如下非线性控制律: (12) (13) 其中: 式中,d1e与dae分别为控制量d1与da的稳态值。x1e,x2e,x3e分为电感电流iL,电压va与vb的稳态值。现不妨假设xor与yor为一次近似线性系统(13)的参考轨迹,对于该参考轨迹必然存在uor使得xor,yor,uor满足系统(13)。选取线性非奇异阵Ts,对状态变量和参考变量做线性变换xs=Tsxo与xsr=Tsxor,把系统变换为龙伯格(Luenberger)能控标准形如下所示: (14) 其中: 龙伯格(Luenberger)能控标准形求解的详细步骤见文献[21]这里不多赘述。对于式(14)必有xsr,uor,满足该式,于是有如下等式: (15) (16) (17) 将上面所提的目标全息反馈非线性控制方法用于近似后的一阶线性系统可得(14)的控制律的矩阵形式为 (18) 将式(18)所得的线性控制律代入式(14)中减去式(15),结合式(17)可得 (19) 上式可化简为 (20) 其中: (21) (22) 式中: 以上证明了目标全息反馈非线性控制方法是通过选取反馈系数来配置SIDO Boost 变换器系统的极点,从而迫使关心的状态变量收敛于各自的参考轨迹, 从而可以绕过非最小相位系统对系统进行直接控制。 为了验证控制策略的正确性,在MATLAB/Simulink平台上搭建了电流连续模式下的SIDO Boost变换器的仿真模型如图4所示,同时以共模-差模电压控制策略作为比较策略[22]。系统仿真参数同表1中一致。将表1参数代入增益公式(2)中可以解得(d1e,dae)=(0.46,0.79)。现取反馈参数k1=40 000,k2=60 000,k3=60 000,由上一节的分析可以算出在该参数下系统的极点为s1=-2 070,s2=-22 100,s3=-60 000,可以看出极点s2与极点s3离实轴的距离均比极点s1离实轴的距离大5倍以上,系统可看成单极点系统,即系统的响应无震荡过程。 图4 目标全息反馈非线性闭环控制框图 图5中展示了当电阻Ra从20 Ω 跳变至 100 Ω 再从 100 Ω跳变回 20 Ω,即等效于电流ia发生变化从1.5 A跳变到0.3 A再跳变回1.5 A时系统的响应波形。从图5中可以看出在两种控制方法下系统都可以做到没有稳态误差,但是动态过程却有所不同。当电流ia从1.5 A跳变到0.3 A时,在所研究的策略控制下电压va最大电压变化为0.7 V且经过2.3 ms恢复到稳定值,而vb基本无变化。在共模-差模电压控制策略控制下va最大变化为3.43 V,经过 20.56 ms恢复稳定值,vb最大电压变化为3.12 V,经过26.12 ms恢复稳定。当电流ia从0.3 A突变回1.5 A时,所研究控制策略下电压va最大电压变化为1.3 V且经过1.2 ms后恢复到稳定,而vb最大电压变化为0.26 V,恢复稳定的时间为0.5 ms。在共模-差模电压控制策略下va和vb最大变化电压分别为3.48 V和2.84 V。它们的恢复时间分别为17.8 ms和16.64 ms。可以看出当a支路负载发生变化时,在所研究控制策略下无论是a支路本身的自我调节还是对b支路的交叉影响均比在共模-差模电压控制策略下的自我调节和交叉影响要小。 (a) 目标全息反馈非线性控制仿真 图6展示的是电阻Rb从10 Ω 跳变至 40 Ω 再从 40 Ω 跳变至 10 Ω,即等效于ib从1 A跳变到0.25 A再跳变回1 A时系统响波形。可以看出当ib从0.25 A变化到1 A时,在所研究控制策略下电压va和vb分别经过1 ms和0.1 ms就能恢复到稳态值,且过冲电压分别为0.29 V和0.05 V。比起共模-差模电压控制策略下的0.57 V和0.71 V的过冲电压要小,同时恢复时间更短。当ib从1 A变化到0.25 A时,所研究控制策略下vb基本不变,其对va的交叉影响为0.25 V且恢复时间仅为1 ms,其小于共模-差模电压控制下的0.67 V和6 ms。总的来说,在电阻Rb变化下所研究的控制策略不仅使本支路具有更快的动态响应且抑制了电压变化,而且还可以减少a支路受到的交叉影响,且受扰后两支路的输出电压响应无震荡过程,为单极响应,验证了上述推论。 (a) 目标全息反馈非线性控制仿真 文中首次将目标全息反馈非线性控制引入至多输入多输出直流变换器中。建立SIDO Boost变换器的仿射非线性模型,随后采用目标全息反馈非线性控制方法设计出系统的控制律,完成了SIDO Boost变换器非线性控制律输出的PWM调制。同时指出所研究方法与EFL方法一样,可以绕过非最小相位系统对目标进行控制,但相比于完全精确线性化,其使用条件更为宽松。文中还证明了该方法控制的原理是通过调节系统非线性控制律的系数Ks去影响SIDO Boost变换器系统的极点分布。最后通过仿真实验验证了在与共模-差模电压控制策略相比下,所设计的控制律能使SIDO Boost变换器具有强的鲁棒性和快速的动态响应,极大程度上抑制了系统的交叉调节。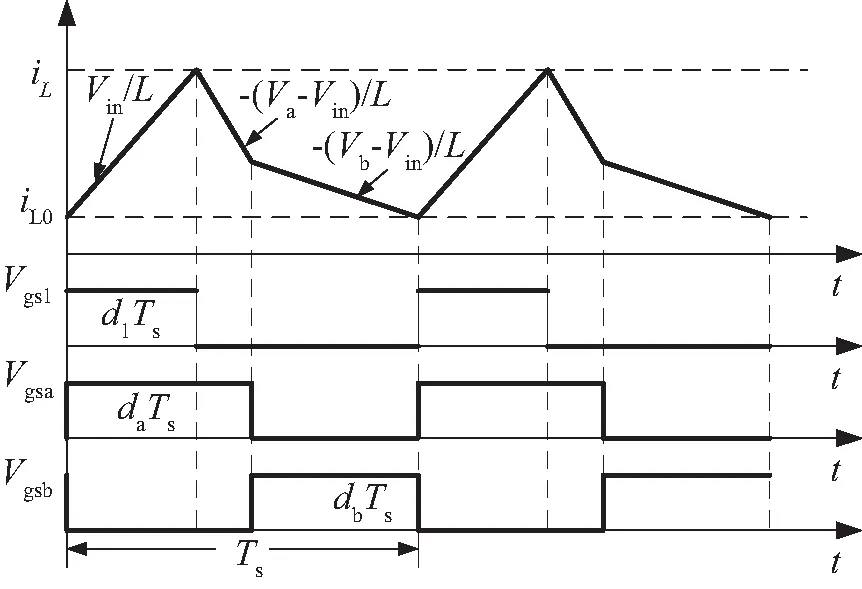
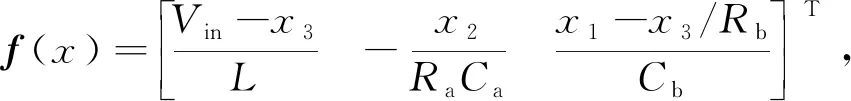

2 SIDO Boost 变换器目标全息反馈非线性控制设计

3 SIDO Boost 变换器极点配置
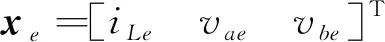
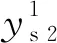
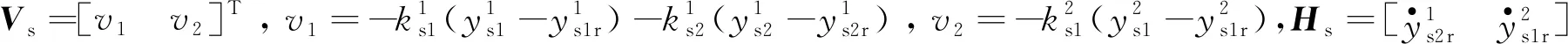
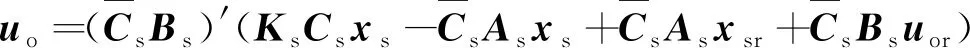
4 仿真实验与分析
5 结语

