光伏逆变并网系统阻抗建模及其稳定性分析

宋绍剑，贺玮彤，刘斌，陆益民，廖碧莲

(广西大学 电气工程学院， 广西 南宁 530004)

0 引言

随着大规模光伏和风电等新能源通过电力电子变换器接口接入电网，由于电力电子变换器接口具有响应速度快和惯性小等特点，加上光伏和风电等新能源电源自身固有的随机性和波动性等特点，新能源并网变换系统与电网之间的动态交互作用带来的一种新型的次/超同步振荡(sub-/super synchronous oscillation, SSO/SSR)问题[1-3]，严重威胁系统稳定和设备安全。

目前分析此类SSO问题产生机理的方法大致可以分为时域分析法[4-7]和频域分析法[8-13]两大类。其中，时域分析方法又可以进一步细分为基于电磁暂态模型的仿真分析法[4-5]和基于系统状态空间模型的特征根分析法[6-7]。通过建立系统的状态空间模型，利用特征根分析法可以分析系统的SSO动态特性，再联合电磁暂态仿真还可以进一步交叉验证特征根分析结果的可靠性。然而特征根分析法存在两方面不足：一是，将电网模型并网系统与光伏模型合并为一个整体进行建模，只要系统稍微发生变化，就需要重新建模。二是，建模过程需要知道系统的详细结构和参数，而在实际工程中这些数据通常由于设备制造商的商业机密而难以获得。阻抗分析法[8-12]和频率扫描法[13]是两种广受关注的两种频域分析法，为分析新型SSO问题提供了一种简单而有效的新型SSO问题分析方法。阻抗分析法只需要并网逆变器的阻抗模型和并网点(point of common coupling，PCC)的电网阻抗信息，就可以通过奈克斯特等稳定判据分析系统的稳定性，因此即便是在电网结构和变换器控制参数无法获得，缺少系统解析阻抗模型的情况下，仍然可以通过频率扫描实验获得逆变器输出阻抗和PCC处的电网阻抗信息。阻抗建模一般分为dq轴线性化建模[14-15]和谐波线性化建模[16-18]两种方法。文献[15]采用dq轴线性化方法进行建模，但是dq轴线性化方法在建模过程中会忽略d轴与q轴之间的耦合效应，所建立的模型准确性受到影响。采用谐波线性化方法[18]进行阻抗建模，由于三相并网逆变器的相序变换是线性时不变的，所以在三相系统中正序和负序阻抗通常是解耦的，因此较于dq轴建模方法，模型相对更加准确。

然而，在上述阻抗建模方法[14-18]通常忽略变换器直流侧电压的动态性和变换器交直流两侧存在的频率耦合影响，导致阻抗模型精度低，进而造成稳定分析结果准确性不高，甚至得到错误的结论。为此，文献[19-22]在对并网系统进行阻抗建模和稳定性分析时开始考虑频率耦合的影响。这些文献多数关注风力发电系统中存在的频率耦合特性。尽管文献[19]详细分析了集中式光伏并网系统内部的频率耦合机理，首次建立了一种计及频率耦合和控制策略的集中式光伏并网系统阻抗模型，量化分析了频率耦合项和直流母线电容大小对系统稳定性的影响，但在考虑最大功率点跟踪(maximum power point tracking, MPPT)控制策略对系统阻抗模型的过程中，仅讨论了一种比较简单的恒电压法MPPT控制。

近年来，随着分布式光伏发电的快速发展，采用两级变换器结构的组串式光伏发电系统受到广泛关注[23-25]。它主要由光伏阵列、Boost(DC/DC)变换器和DC/AC逆变器组成，MPPT控制策略通常在Boost变换器中实现。

目前常用的光伏发电系统MPPT方法主要包括：恒定电压法、扰动观察法、爬山法、增量电导法和模糊控制法等[26-28]。其中，模糊控制法[27-28]的思想与扰动观察法、爬山法等相似，且具有精度更高的优点。不过，除了恒定电压法外，这些方法在实际工程应用中存在两个问题：①跟踪过程存在小幅功率振荡现象，容易引起直流母线电压的波动，造成两级组串式光伏并网系统前后两级变换器的功率耦合和逆变器交直流两侧的频率耦合现象。②多数MPPT控制策略的解析模型难以获得，难以与并网逆变系统的阻抗模型集成。

为此，本文提出一种考虑逆变器频率耦合和最大功率点跟踪控制策略影响的新型阻抗建模方法，并分析不同频率耦合因素对系统总体阻抗特性及其稳定性的影响。主要贡献如下：

① 利用模糊控制与PD控制的等价性原理，建立了模糊MPPT控制策略的等效数学模型，以便于将模糊MPPT控制策略集成到并网逆变系统阻抗模型，建立系统的整体阻抗模型；

② 建立了考虑变换器交流和直流两侧频率耦合且包含MPPT控制策略的组串式LCL型光伏并网系统整体阻抗模型；

③ 总结了直流母线电压动态和MPPT控制策略对光伏并网系统频率耦合特性和稳定性影响的规律。

1 并网系统频率耦合特性建模

典型的光伏发电系统一般由光伏阵列、Boost升压电路、并网逆变器等组成，如图1所示。并网逆变器采用电压外环+电流内环的双闭环PI控制结构，主要包括锁相环PLL、abc/dq(Park变换)、直流母线电压控制环、电流控制环、dq/abc(Park逆变换)、脉宽调制PWM模块。在图1中，Upv，Ipv是光伏阵列输出的电压与电流，滤波电容C、储能电感L、电力二极管D和功率开关管IGBT构成Boost电路。PCC处的三相电压和电流分别记为va，vb，vc，ia，ib和ic，逆变器三相输出端口电压分别记为via，vib和vic，电网电压分别记为vga，vgb和vgc，Zg是电网阻抗，Vdc是直流母线电压，Cdc是直流母线电容，idc是直流母线电流，电感L1，L2，电容Cf与阻尼电阻Rd构成了LCL滤波器，θPLL为经过PLL得到的电网电压相角，Vdc_ref是直流母线参考电压。

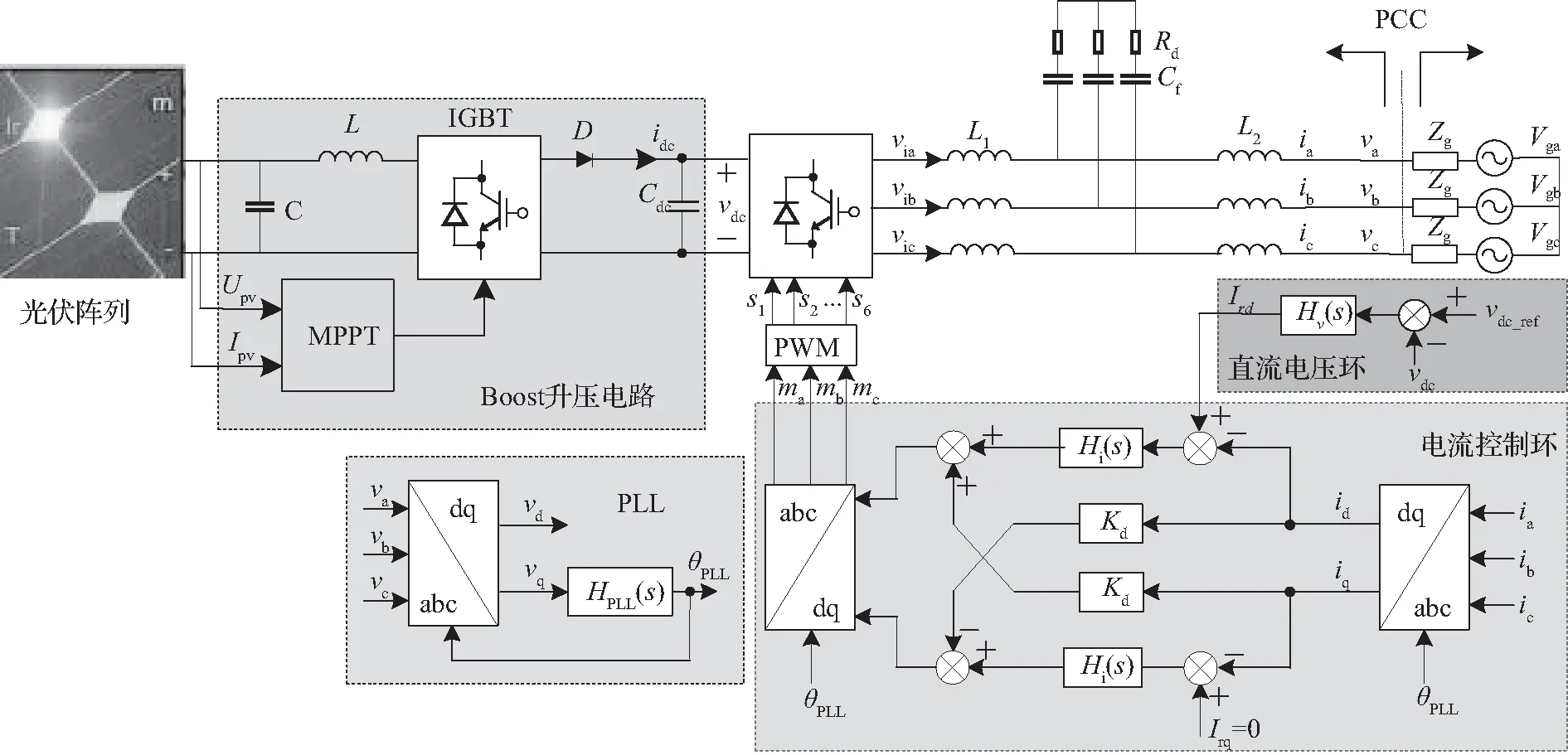
图1 光伏并网系统结构示意图

由于在直流侧母线电压、PLL和不平衡电流控制等环节存在复杂的频率耦合关系，详细的分析过程详见文献[19]，限于篇幅限制，在此不再赘述。下面重点介绍计及频率耦合的并网逆变系统的阻抗建模过程。

1.1 主电路的平均模型

根据图1可以建立光伏并网逆变系统主电路的平均模型为

(1)

(2)

当并网逆变器存在频率耦合时，为了更具一般性，假设并网点扰动电压包含正序分量和负序分量，此时并网点a相电压、电流的时域表达式为

va(t)=V1cos(ω1t)+Vpcos(ωpt+φvp)+Vncos(ωnt+φvn)，

(3)

ia(t)=I1cos(ω1t+φi1)+Ipcos(ωpt+φip)+Incos(ωnt+φin),

(4)

式中，V1为基频电压幅值;Vp为正序扰动电压幅值;Vn为负序扰动电压幅值;I1为基频电流幅值;Ip为正序的电流响应幅值;In为负序的电流响应幅值;f1为基波频率;φvp为正序扰动电压的相位;φvn为负序扰动电压的相位;φi1为基频电流的相位;φip为正序的电流响应的相位;φin为负序的电流响应的相位。

将公式(3)、(4)进行傅里叶变换，可以得到频域下a相的电压、电流表达式：

(5)

(6)

式中，变量Vp=(Vp/2)e±jφvp，式(5)、(6)中的其他变量的表达式与前文类似。

1.2 控制环建模

1.2.1 直流电压控制环的小信号建模

目前大多数并网逆变器的阻抗建模过程中通常将直流母线电压视为理想电压源，忽略直流电压控制环对阻抗模型的影响。由于直流电压控制环是光伏并网逆变系统产生频率耦合的重要影响因素之一，因此，建立计及光伏并网逆变器交直流两侧频率耦合的序阻抗模型时必须考虑其影响。

根据并网逆变系统平均模型，将公式(1)代入公式(2)，可以得到直流母线电压与并网点三相电压和三相电流的关系。

根据图1可知，直流母线电压Vdc与额定的直流母线电压Vdc_ref之差经过直流电压控制器后作用到电流环的d轴。将公式(1)代入(2)中，结合公式(3)和(4)，可以得到PCC处的abc三相电压和电流跟直流母线电压Vdc的关系，把时域形式的直流母线电压方程变为频域形式：

(7)

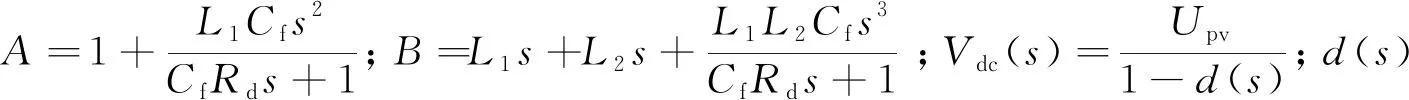
根据图1中左上框图内的直流母线控制环可知，输入到电流环d轴的叠加电流Ird的表达式为

Ird[±fp]=Vdc[±fp]Hv(s),

(8)

式中，Hv(s)是直流电压控制器的传递函数。

1.2.2 锁相环的小信号建模

图1中的左下框为锁相环控制策略，当PCC处存在扰动时，电网电压相位的表达式为

θPLL(t)=2πf1t+Δθ(t),

(9)

式中，Δθ(t)是θPLL(t)的扰动分量，由PCC处的扰动造成的角度偏移。

因Δθ(t)=HPLL(s)Vq，Vq=-[V1sinΔθ+Vpsin(Δθ+θ1-θp-φvp)+Vnsin(Δθ+θ1-θn-φvn)],

(10)

得到Δθ为

(11)

则θPLL的扰动分量与并网点电压扰动的关系满足：

Δθ[±fp]=∓jTPLL(s)Vp±jTPLL(s)Vn，

(12)

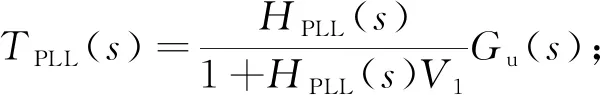
1.2.3 电流环小信号建模

图1中的右中框为电流环控制策略部分，它将三相电流进行Park变换后，进行dq坐标下有功和无功的解耦控制。根据图1可知，三相电流进行Park变换时所需的θPLL由公式(8)中的电网电压相位确定，因此可以得到频域下的dq轴电流表达式：

(13)

化成频域表达式为

(14)

(15)

电流控制器的输入为dq轴参考电流，输出为dq轴调制信号。

根据上述公式，可以得到调制信号的扰动分量表达式为

(16)

静止坐标系下a相的调制信号表达式可以通过坐标变换得到，通过频域卷积运算可以得到：

Ma=Md[dc]cosθPLL[±fp]+Md[±fp]cosθPLL[dc]-Mq[dc]sinθPLL[±fp]-Mq[±fp]sinθPLL[dc],

(17)

并网逆变器a相输出端口电压满足：

via(t)=Kmvdc(t)×ma(t),

(18)

式中，Km是调制系数。

因此，逆变器a相输出端口电压的频域分量等于直流母线电压的频域分量与a相调制信号频域分量的卷积，即

(19)

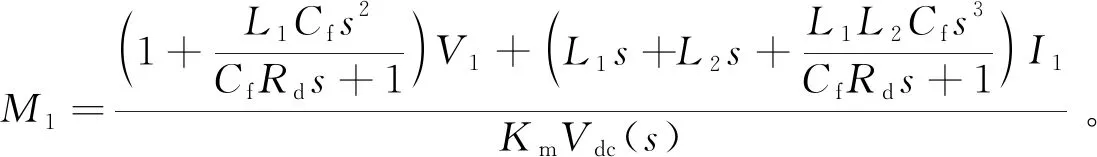
(20)

1.2.4 光伏并网逆变器输出阻抗与频率耦合建模

结合式(7)、(12)和(19)可以得到光伏并网逆变器的输出阻抗与频率耦合模型。

正序电压扰动与负序电压扰动对正序电流响应分量影响的模型分别如下：

(21)

(22)

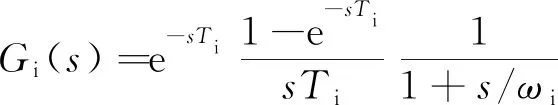
(23)

(24)

(25)

(26)

1.3 Boost电路模型

1.3.1Boost主电路模型

根据图1中Boost升压电路的平均模型有

(27)

通过式(27)可以计算得出Boost电路的模型:

(28)

1.3.2MPPT环节数学模型

本文的两级式光伏并网逆变系统的MPPT控制策略在Boost逆变器中实现，所采用的模糊MPPT控制策略。它的结构如图2(a)的上半部分所示，可分为模糊化、控制规则和去模糊化三个模块。模糊控制的主要特点是将专家经验和知识融入到语言规则中，通过模糊推理来实现类人智能控制。模糊控制法能够快速跟踪系统的最大功率，在稳定条件下，到达最大功率后基本没有波动，即具有更好的动态和稳态性能。但是在建立解析模型时，由于模糊控制中有不连续的环节，难以直接给出对应的传递函数，因而本节利用位置式模糊控制与PD控制具有等价性[28]原理，求解其等价的数学模型。其中：位置式模糊控制输出如下：

(a) 模糊控制与PD控制等价示意图

u(k)≈ku×ke×e(k)+ku×kec×[e(k)-e(k-1)]。

(29)

而PD控制输出可以写为

u(k)=Kp×e(k)+Kd×[e(k)-e(k-1)]。

(30)

通过式(29)和(30)对照，可以得出结论，位置式模糊控制与PD控制具有等价性。

利用这个等价性，可以计算MPPT部分的数学模型。图2(a)是模糊控制与PD控制的等价性示意图，图2(b)是加入一个扰动后的跟踪效果对比图。从图2可看出，模糊控制与PD控制具有等价性。基于模糊控制的MPPT技术的模型通常采用五模糊级结构，包括NB(负大)、NS(负小)、ZE(零)、PS(正小)、PB(正大)。为了保证输出变量的对称性，必须仔细设计具有5个模糊子集的隶属度函数。图3展示了设计的具有5个模糊子集的隶属度函数，ΔV和ΔP分别是输入模糊控制器的电压和功率的误差，ΔD表示为DC-DC控制器的占空比。模糊规则的数量设为25条，各条模糊规则按常见的人工经验进行设置，模糊控制规则见表1。通过计算可得，MPPT环节的数学模型为

表1 模糊控制规则表

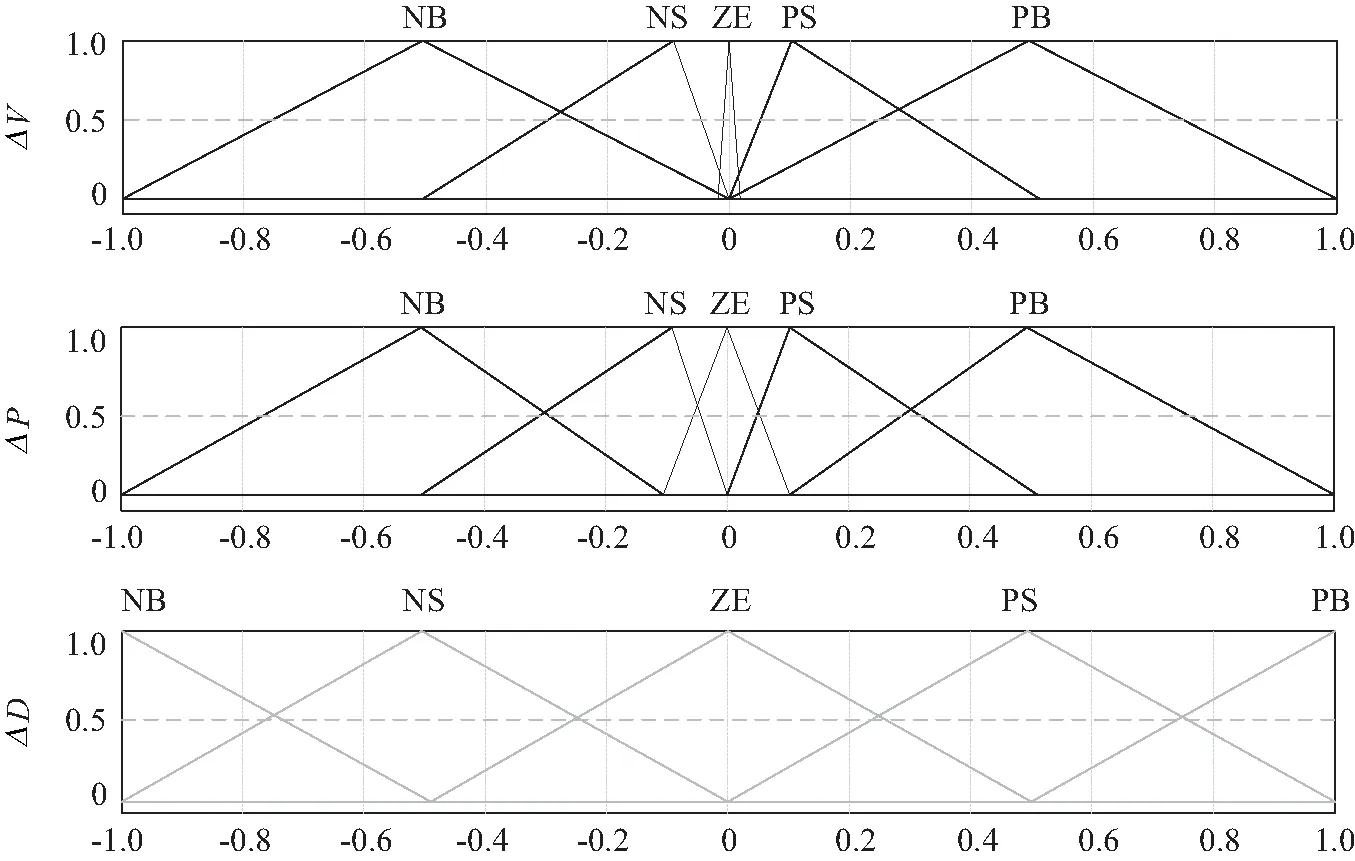
图3 5个模糊子集的隶属函数

(31)

1.4 组串式并网逆变系统整体模型

两级组串式并网逆变系统的数学模型可以通过光伏并网逆变器和Boost电路模型串联等效而得，组串式并网逆变系统整体正序和负序阻抗模型如下：

Zpp1=Zpp′+ZBoost,

(32)

Znn1=Znn′+ZBoost,

(33)

其中，如图4所示，Zpp′=Zpp+Znp和Znn′=Znn+Zpn是考虑频率耦合后的正序和负序等值阻抗，ZBoost是Boost电路模型。

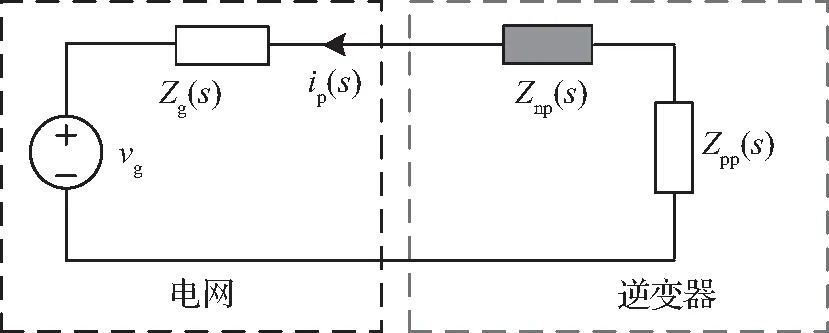
图4 输出阻抗与频率耦合项的关系

2 算例分析

为了验证本文所提方法的有效性和先进性，建立了一个1 MW的组串式并网光伏逆变系统，具体的半实物仿真实验平台如图5所示，系统详细参数如表2所示。下面重点从直流母线动态以及是否考虑MPPT环节这两个因素对并网系统稳定性产生影响进行仿真和实验验证。限于篇幅限制，锁相环带宽和不对称电流控制产生的频率耦合及其对系统稳定性的影响可以参考文献[19]，在此不再赘述。

图5 基于RT-LAB硬件在闭环仿真示意图

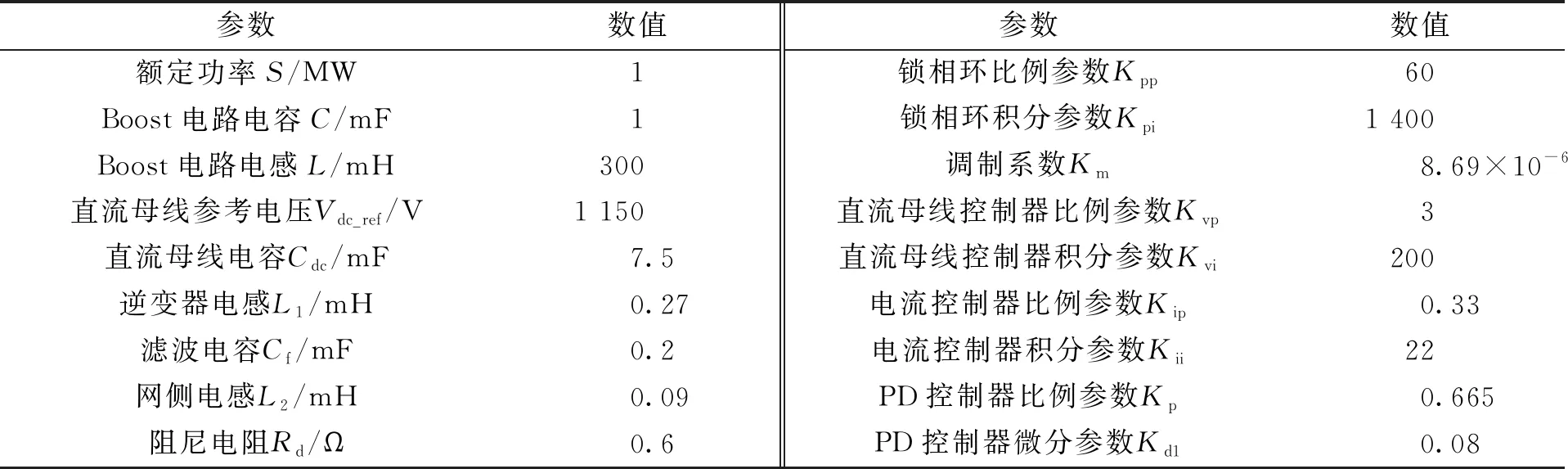
表2 光伏并网逆变器仿真参数

2.1 并网系统的输出阻抗与频率耦合特性

根据光伏并网系统阻抗模型式(32)，(33)可以绘制出逆变器输出阻抗及其频率耦合项的正、负序特性曲线，如图6所示。由图6可以知道，在低频段(30～150 Hz)逆变器的阻抗与频率耦合的幅值比较接近，但在高频段(5～16 kHz)范围，频率耦合的幅值远远大于逆变器的阻抗，因此频率耦合对于逆变器阻抗的影响主要集中在两倍基频附近。

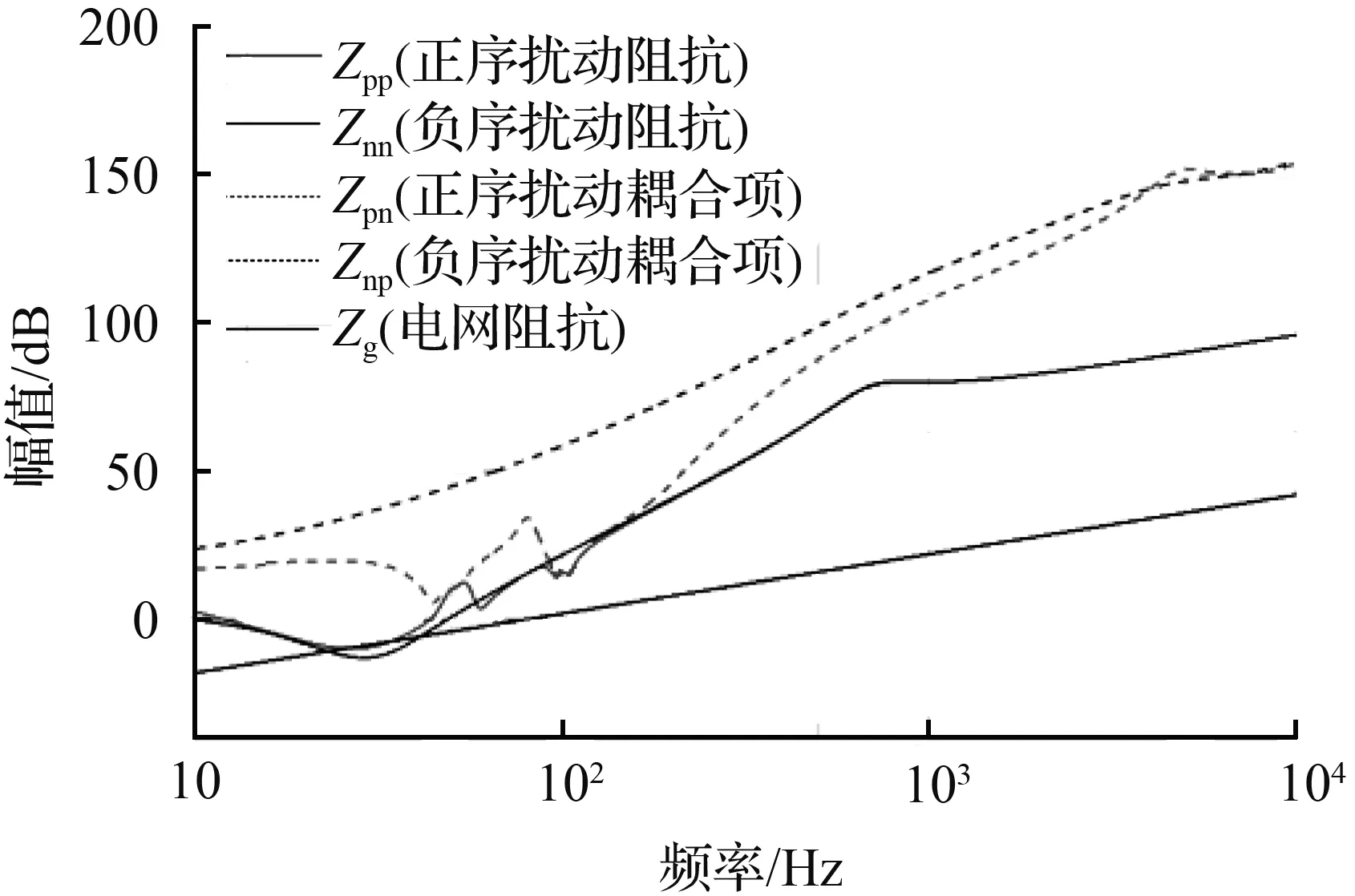
(a) 幅频曲线

2.2 并网系统稳定分析

为了分析在不同强度的电网条件下(一般用SCR，Short Circuit Ratio表示，SCR<3为弱电网。)考虑频率耦合影响的光伏并网系统的稳定性，接下来分析不同SCR情况下的并网系统的稳定性。式(32)给出了组串式逆变系统输出阻抗与频率耦合的模型，当电网阻抗Lg=0.125 mH(SCR=4)时，结合表2中的参数可以得到逆变系统有效输出阻抗曲线与电网阻抗曲线，如图7所示。通过对图8的直流母线电压曲线、图9的并网点三相电流波形和图10的并网点电流总谐波失真(total harmonic distortion, THD)进行联合分析，可以看出是此时的并网电流谐波很小，系统是稳定的。

图7中的逆变器有效输出阻抗曲线与电网阻抗曲线在低频段并未出现交点，与图10中的THD分析结果一致，交叉验证了在系统没有出现谐振点及对应的谐波分量。

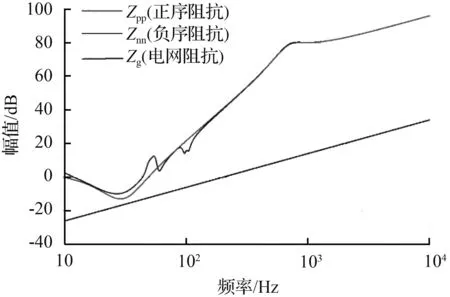
(a) 幅频曲线

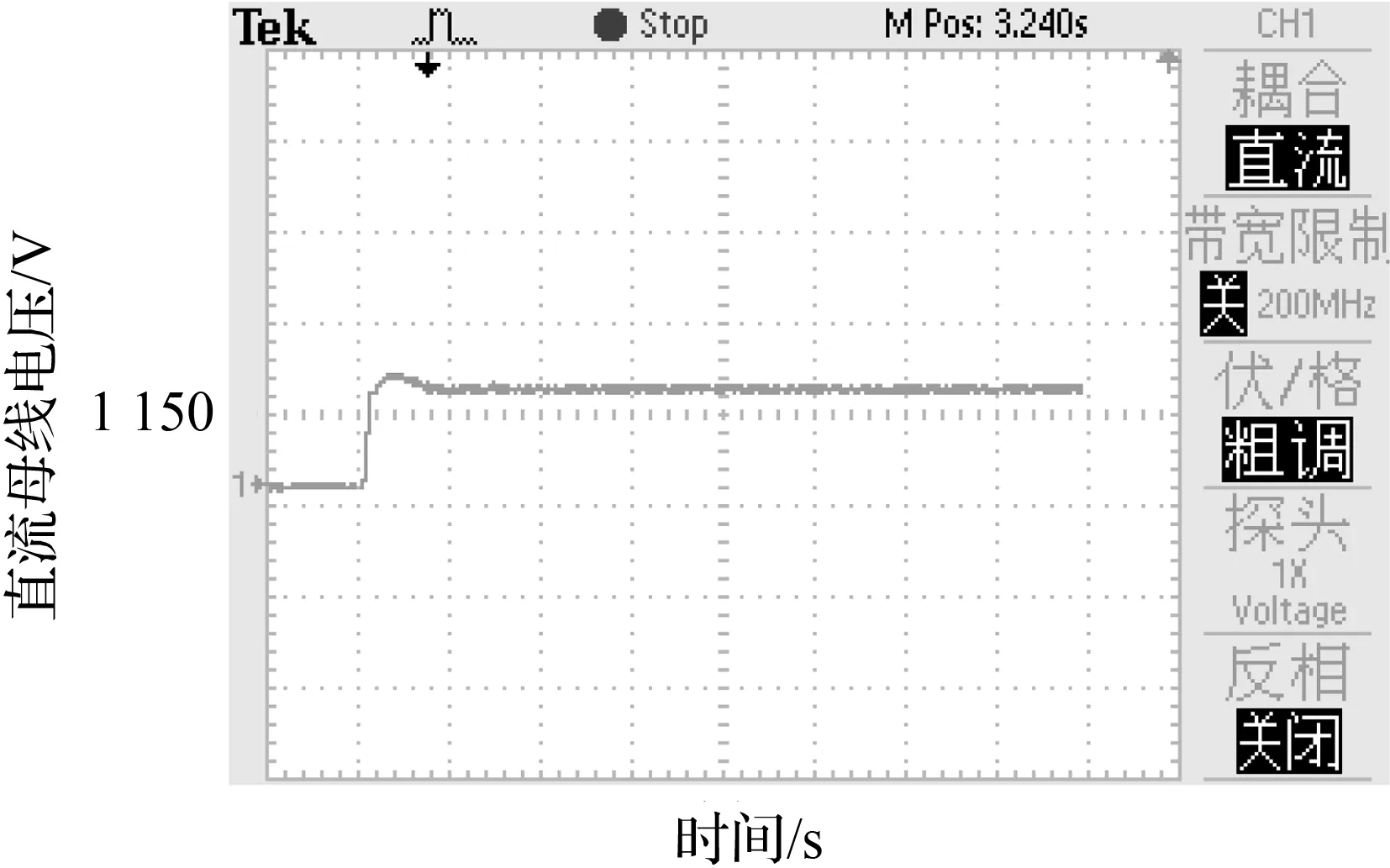
图8 直流母线电压 (SCR=4)

图9 系统并网点处三相电流 (SCR=4)

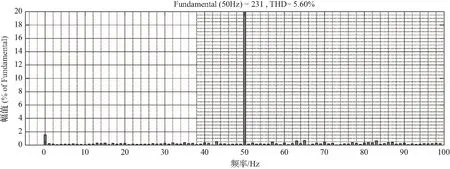
图10 PCC点电流THD (SCR=4)

2.2.1 MPPT环节对频率耦合的影响

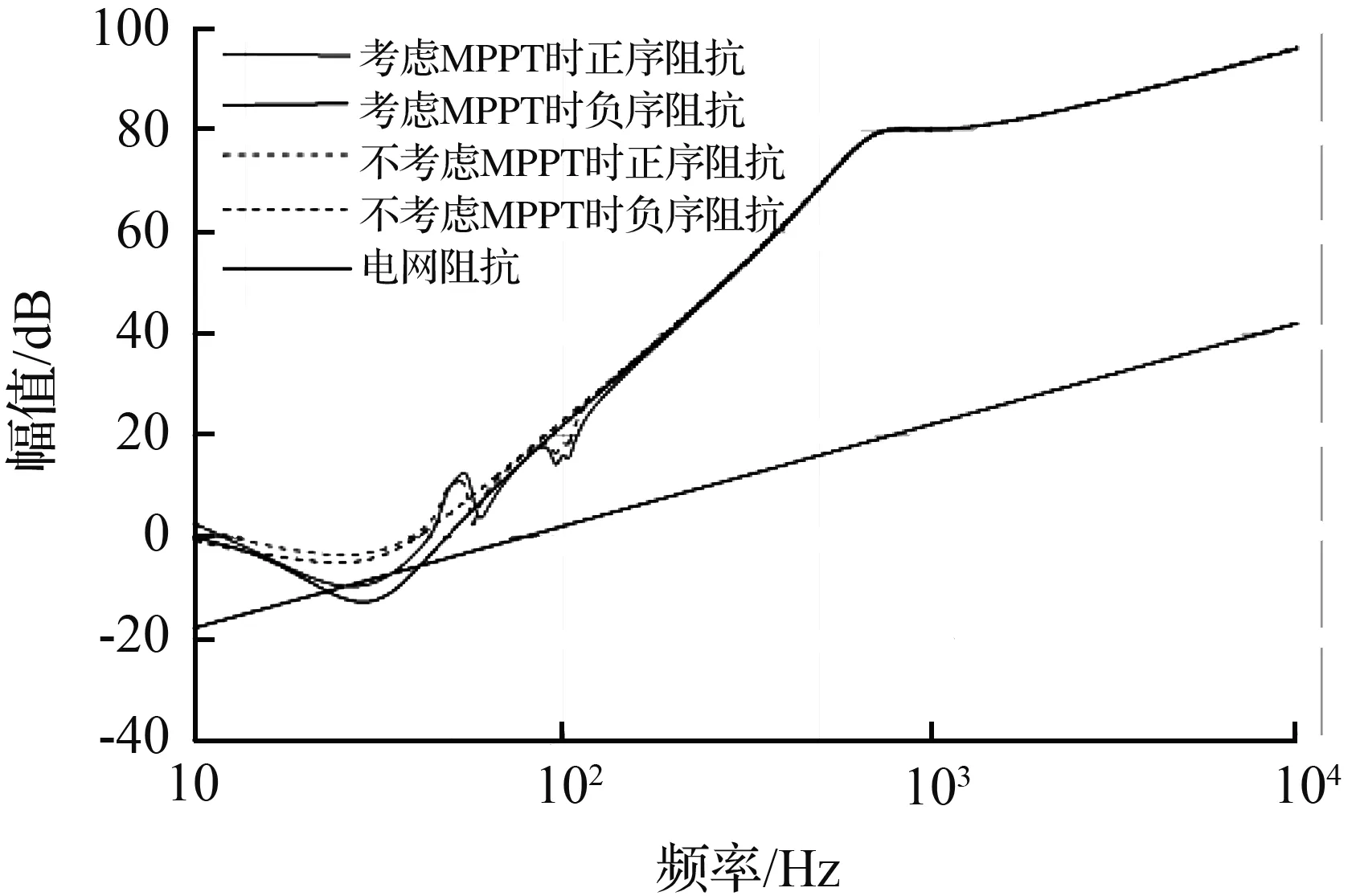
为了验证MPPT环节对组串式光伏逆变系统稳定性的影响，图11给出了是否包含MPPT环节的两种光伏逆变系统输出阻抗的对比结果。

由图11可以看出加入MPPT环节后，逆变系统的耦合现象更加明显。证明了前级环节对频率耦合现象是有影响的。加入MPPT环节，可以让系统的耦合现象更加明显，也就能更准确地预测系统潜在的谐振点。(注：接下来的实验皆采用包含MPPT环节的模型。)

(a) 幅频曲线

2.2.2 非理想直流母线电压对耦合现象影响

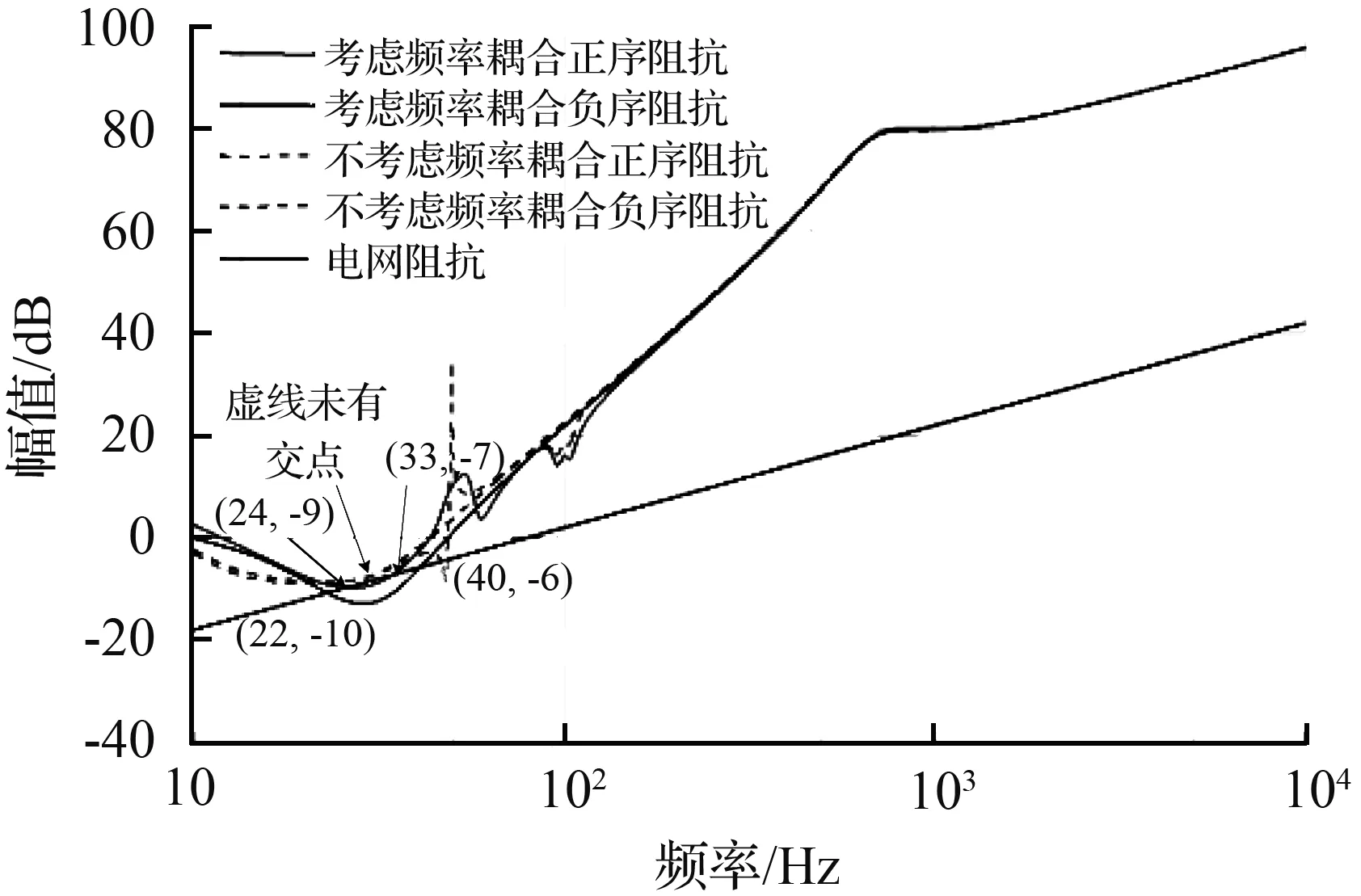
为了分析非理想直流母线电压条件下，光伏并网逆变系统与弱交流电网交互产生的频率耦合现象，将电网阻抗增大到Lg=0.25 mH(SCR=2)，模拟弱电网环境运行环境；同时，通过系统模糊MPPT控制策略调节过程引起的直流母线电压波动来模拟光伏逆变器的非理想直流母线电压条件。从图12可见，弱电网条件下(SCR=2)，频率耦合效应更为显著，考虑频率耦合的正序阻抗曲线与电网阻抗在24 Hz处有一个潜在谐振点，而未考虑频率耦合时则未出现。随着光照的变化时，直流母线电压会产生一定的波动，如图13所示。此时直流母线电压不再是非理想电压，逆变器对应的并网电流波形如图14所示，可以看到PCC处并网三相并网电流发生了明显的畸变，相应的电流THD分析如图15所示。

(a) 幅频曲线

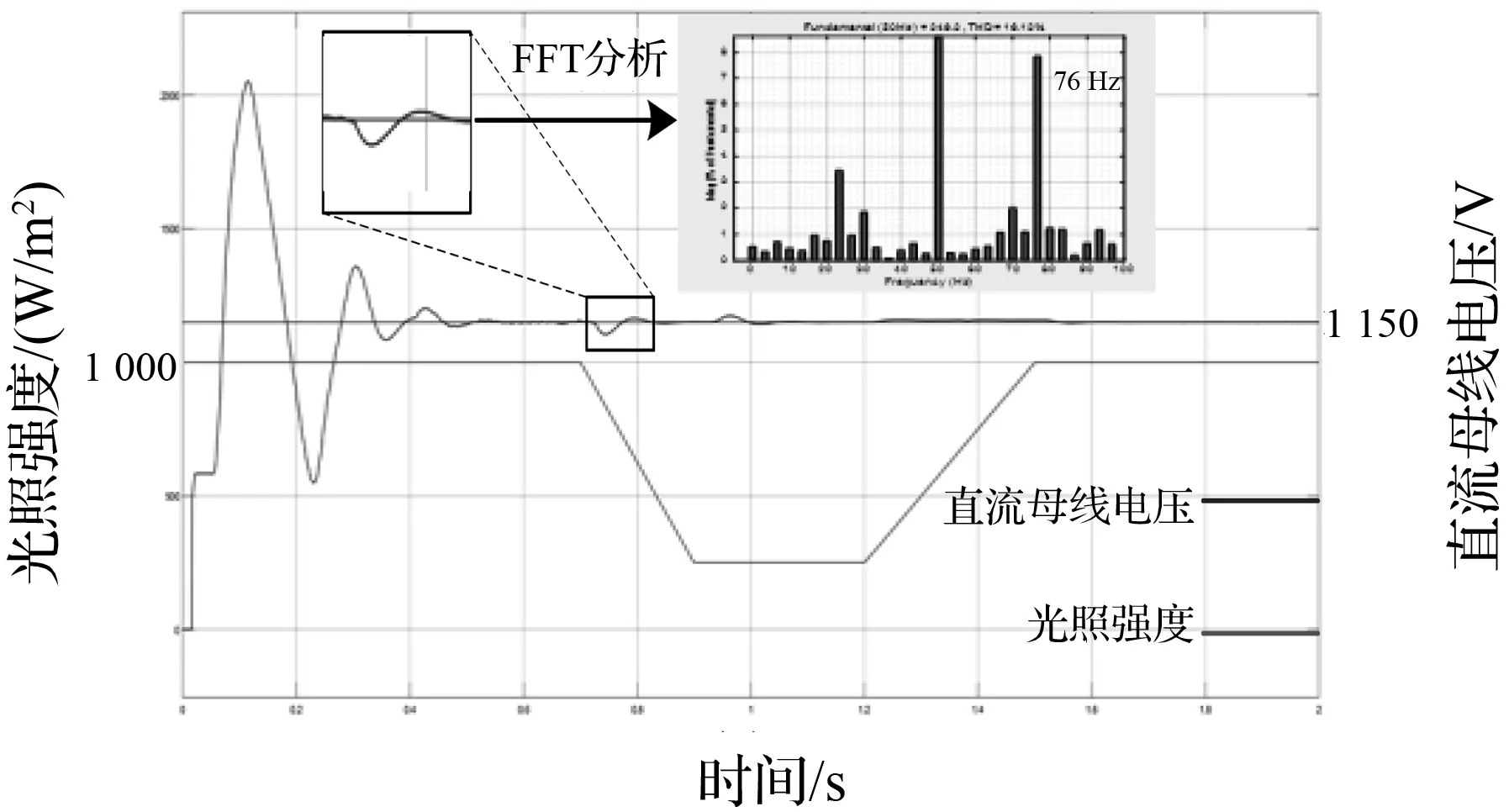
图13 加入MPPT环节后，直流母线电压 (SCR=2)

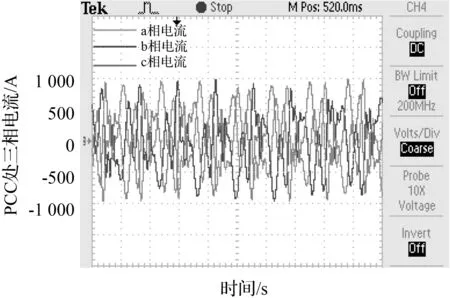
图14 加入MPPT环节后，系统并网点处三相电流 (SCR=2)

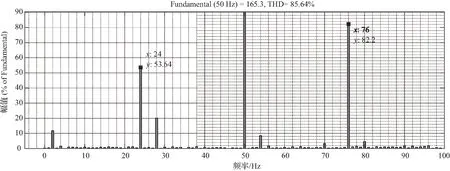
图15 加入MPPT环节后，PCC点电流THD分析 (SCR=2)

根据图14的三相电流可看出，由于在实现MPPT的过程中，Boost变换器输出的电压存在小幅波动，此时的系统出现了谐波不稳定现象。在图14中，基频(50 Hz)左右出现了谐波幅值最高、频率分别为24 Hz和76 Hz的两个谐波分量。其中，76 Hz是PCC点处注入系统的一个低频电压扰动。同时，24 Hz与图12中的逆变系统正序输出阻抗曲线与电网阻抗曲线交点频率相同，通过时域仿真结果与阻抗模型的数值分析结果的交叉验证，说明系统频率耦合出了一个频率为24 Hz的谐振频率分量。对照图12和图15，可以看出，在不考虑频率耦合的情况下，系统阻抗曲线与电网阻抗没有交点，无法找到潜在的谐振频率点24 Hz。相反，考虑频率耦合及MPPT影响的阻抗模型则可以准确地预测系统潜在的谐振点，模型更为精确。

3 结论

本文建立了考虑频率耦合的组串式光伏并网系统序阻抗模型，同时具体分析了非理想直流母线因素对于频率耦合的影响以及加入前级环节对频率耦合的影响。得到主要结论如下：

① 模糊控制与PD控制间具有等价性，在分析数学模型时，可以运用其等价性对MPPT环节建立准确的数学模型。

② 考虑MPPT环节后的组串式光伏逆变系统，频率耦合现象更明显，更准确地预测系统潜在的谐振点。

③ 考虑MPPT环节后，在非理想直流母线的条件下，光伏系统在低频段附近会产生明显的耦合现象，但在高频段附近，频率耦合现象不明显。