金属材料宽应变率下动态本构模型及其扩展有限元应用

李双蓓，吴园，赵璇，彭林欣*,3

(1.广西大学 土木建筑工程学院， 广西 南宁 530004；2.工程防灾与结构安全教育部重点实验室， 广西 南宁 530004；3.广西防灾减灾与工程安全重点实验室， 广西 南宁 530004)

0 引言

工程中金属材料结构的应用范围很大，随着各类复杂工况的出现，金属材料动态加载下的裂纹扩展分析成为近几年研究的热点[1-2]。采用扩展有限元法可以对此展开较高效的分析[3]，而分析的可靠性首先取决于材料本构模型的准确性[4-5]。研究表明不同加载应变率下的金属材料力学响应存在显著差异[6]。

动荷载作用下，金属往往会产生率敏感性的塑性行为，NICHOLAS[7]研究了软钢、不锈钢、铝合金等多种金属下的动态力学行为，发现均存在应变率效应。ZERILLI等[8]基于材料微观变形机制提出了考虑率效应的物理本构模型。物理型本构方程拟合实验结果精度较高，但是参数多计算复杂应用困难。JOHNSON等[9]对实验数据进行归纳总结，提出了采用对数函数的线性关系来描述应变率敏感性的经验型本构模型，因其形式简单，参数少且易获取，是动载荷作用下金属结构响应与破坏数值模拟考虑应变率效应的常用方法。但是新的研究成果表明，对于许多金属高应变率下的应力应变行为，JC模型描述得并不准确。ZHOU等[10]通过采用JC本构模型对四种金属实验数据拟合分析发现，传统JC模型适用于中低应变率下的金属材料，对于高应变率下的某些金属材料，会对材料应力有所低估。COWPER等[11]的研究说明高应变率下金属材料的流变应力与应变率的关系用幂函数表达更为贴切。李云飞等[6]考虑绝热温升影响，通过构造功热转换系数与应变率之间的函数关系来对JC模型进行修正，并利用局部补偿优化模型参数，以更准确描述Ti-6Al-4V钛合金在准静态与高应变率下的本构行为。惠旭龙等[12]对准静态与中高应变率下的2A16-T4铝合金的动态力学性能进行研究，基于对数为底的幂函数对JC应变率项进行修正，拟合结果与实验数据相吻合，但实验中2A16-T4铝合金在中低应变率下几乎率不敏感。

研究成果表明，目前仍缺乏一种针对多金属宽应变率敏感下的通用动态本构模型，以往金属本构模型多针对于准静态或高应变率单一区间进行研究，而金属动态加载受力复杂往往不局限于一个应变率区间，因此完备宽应变率下的金属动态通用本构模型具有重要意义。

本文将针对常用经验本构模型在常温下宽应变率范围内的适用性进行探讨分析，基于不同应变率范围下流变应力的函数表现，提出适用于宽应变率下的金属动态本构JC-CS模型，并结合20CrMnTi钢、Q420钢和Ti-6Al-4V钛合金三种金属材料在低中高等不同应变率下的实验数值验证其准确性与通用性。通过ABAQUS平台的UEL用户子程序进行二次开发，导入新本构模型JC-CS，并将新模型与扩展有限元结合，在ABAQUS/Standard中进行金属材料三点弯曲梁在动荷载作用下含不同初始裂纹的动态裂纹扩展分析，实现JC-CS模型在有限元软件中的拓展应用。

1 构建宽应变率动态本构模型

1.1 JC模型和CS模型

Johnson-cook(简称JC)本构方程是被广泛应用的一种金属动态本构模型，其将金属材料的流变应力表示为应变、应变速率和温度项的乘积，基本形式如下：

(1)

对于大部分金属而言，其塑性变形阶段在低应变率(或恒应变率)时，流变应力近似为应变的幂函数关系，与应变率的关系JC模型假设为对数的线性关系，而对数曲线在自变量达到一定数值后，因变量随着自变量的增长呈不明显的变化趋势，很难对率敏感性金属材料的高应变率阶段进行描述，因此JC模型不适用于描述宽应变率下的金属本构关系。

Cowper-Symonds(简称CS)模型采用幂函数的线性关系来表达动态流变应力与应变率的关系，这在许多金属高应变率加载研究中得以应用。其形式为：

(2)

式中，σ0为静态流变应力；D，q是材料常数，一般大于零。对于宽应变率下的本构关系描述，CS模型也存在着拟合上的缺陷，无法准确表达低应变率阶段率敏感材料的属性。主要原因是JC模型在应变率项对数函数中考虑了参考应变率的影响，对等于参考应变率或低于参考应变率的本构关系可以描述得相对准确。而CS模型以参考应变率时的流动应力为基础乘以数值大于1的应变率项，高估了参考应变率及其以下的流变应力，有研究[11]表明在低应变率0～1 s-1也有金属表现出非常明显的率强化效应。

1.2 JC-CS模型的建立

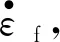
(3)

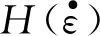
(4)

(5)

金属在高应变率下通常会引起材料温度升高，还需考虑温度软化效应对JC-CS模型进行完善。假设加载过程绝热，常规做法是采用绝热温升表示室温代入到JC模型的温度效应项中[14]，但改进后的模型是多元微积分方程，计算较为复杂，在实际工程及有限元模拟中应用困难。本文参考文献[15]，基于绝热温升为应变的函数，在式(3)的基础上引入参数k，把绝热温升影响直接简化为应变和应变率的相关项。将应变硬化，应变率效应以及温度软化效应进行耦合，从而构建出适用于宽应变率范围金属材料的动态本构模型，形式如下：

(6)

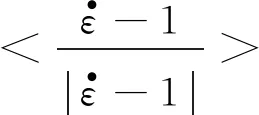
(7)

由式(6)可知，JC-CS模型突出了金属在不同应变率范围下应力应变关系的不同特征，对于不同受力情况如单向拉伸与压缩(中低应变率0～100 s-1)、高速冲击爆炸(高应变率100～10 000 s-1)或落锤冲击(不稳定应变率范围)等下的本构关系都能进行统一描述。不采用针对单一金属的表达函数，适用于各类金属，具有通用性。同时在考虑软化效应上进行了相应简化，方程式简单易于编程，便于导入有限元软件。为宽应变率下金属力学行为的进一步研究提供了参考。

2 JC-CS模型通用性评估

2.1 屈服强度函数拟合分析

采用动态本构模型对试验数据进行拟合时，应变率硬化系数C一般由材料屈服强度给出，因此必须先对屈服强度进行准确拟合。本文分别采用对数函数和幂函数对20CrMnTi钢[14]和Ti-6Al-4V合金[10]的屈服强度进行拟合，拟合结果如图1、图2所示。

(a) 对数函数拟合

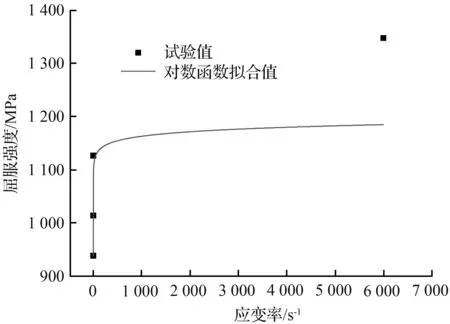
(a) 对数函数拟合

从图1(a)和图2(a)可以看出金属屈服强度有明显的率强化现象，对数函数在拟合过程中应变率达到一定值后，对应的屈服强度值呈平缓的增长趋势，无法描述材料屈服强度随应变率的增大而显著增加的现象。相比之下，采用幂函数来表达高应变率下屈服应力与应变率之间的关系与实验值吻合程度更高，如图1(b)和图2(b)所示。对涵盖低高应变率的金属屈服强度进行拟合分析时，无论是对数函数还是幂函数都有其拟合准确的特定应变率范围，对数函数更适用于较低应变率下的率相关描述，而幂函数无法表达参考应变率附近及其以下范围内率相关的现象，在高应变率区域表现更为优秀。

2.2 宽应变率下金属应力应变关系的预测

本文以20CrMnTi钢[14]、Ti-6Al-4V钛合金[10]以及Q420钢[13]为例分别讨论JC、CS以及JC-CS本构模型在宽应变率下的适用性。这些金属材料应用涉及机械、航空以及建筑工程领域。应变率范围涵盖了0～1，1～100，100～1 000，1 000～6 000低中高各阶段。JC-CS模型的7个待定系数(A，B，n，C1，C2，q，k)可通过试验数据方便获取，其中A、B、n可通过准静态拉伸试验进行标定；在静态本构关系的基础上利用动态拉伸试验(中应变率)和霍普金森压杆冲击试验(高应变率)稳定应变率下的试验数据可标定参数C1，C2，q以及k。JC-CS动态本构模型标定参数值见表1。

表1 JC-CS动态本构模型标定参数值

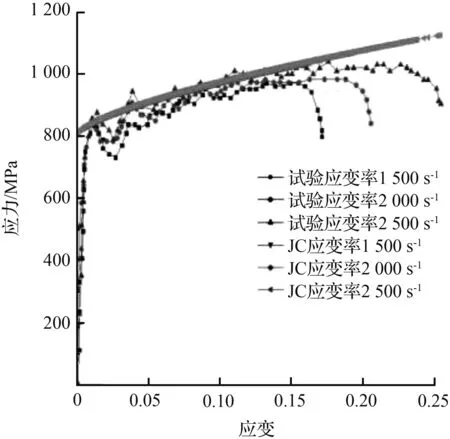
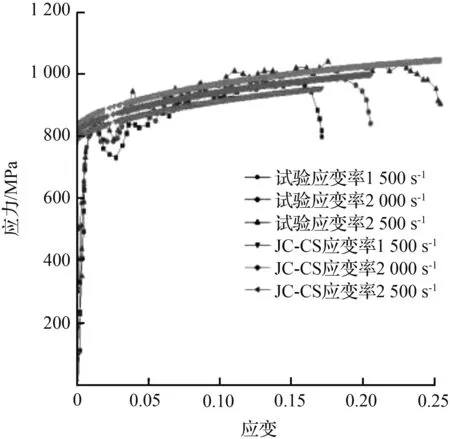
三种金属材料在各应变率下的应力—应变关系，可由标定参数后的式(1)、式(2)和式(6)表达的JC、CS和JC-CS本构模型进行预测，模型计算结果与试验对比如图3至图5所示。

如图3至图5所示，各加载应变速率下的试验结果表明，金属材料在不同的应变率阶段皆有可能出现应变率强化效应，即应力随着应变率的增长而变大。通过图3至图5的对比分析，可以得出以下结论：

(a) 20CrMnTi钢

(a) 20CrMnTi钢

(a) 20CrMnTi钢

① 采用JC模型对应变应力关系进行预测时：高应变率阶段(应变率范围100～6 000 s-1)，计算结果与实验数据误差较大，基本上所有应变率下的应力值都集中在了一条曲线上，造成预测结果应变率影响小或基本没影响的现象，由图3可以看到，整体高估了20CrMnTi钢材料的流变应力，而对于其余金属则表现为低估材料高应变率阶段的流变应力，归结原因是JC模型的应变率项采用对数函数的局限性，无法对高应变率敏感性做出反应。而对于图3(b)和图3(c)中的中低应变率(0～100 s-1)，采用传统JC模型能较贴切地描述金属在此应变率范围下的应力应变关系。

② 如图4所示，采用CS模型进行20CrMnTi钢本构关系描述时，高应变率阶段应变应力曲线能随着应变率的变化而有相应变动，说明幂函数相较于对数函数，在此阶段表达应变率敏感性更为灵活，与试验数据的吻合程度相对也高于JC模型。但CS模型出现了随着应变的增长，预测应力偏离实验数据程度越大的现象，表现出较明显的温度软化效应。且在预测Ti-6Al-4V钛合金应变率为0.000 01 s-1与0.001 s-1的曲线时明显高估了材料的应力，在偏离参考应变率一定范围后，在应变率为1 s-1时又具备了较良好的描述能力。

③ 当应变率在中应变率范围内时，JC模型和CS模型同时具有良好的拟合表现。为了保证低应变率和高应变率范围下的金属动态应力应变曲线也有准确的拟合效果，本文以中应变率区间的中值50 s-1为界定义对数函数与幂函数的对接点，采用开关函数处理，构建适用于宽应变率的动态本构模型，预测结果(图5)与试验值相吻合，表明同时考虑多重因素后的JC-CS本构模型在大范围应变率条件下均能较准确地反映多金属动态加载下的应变硬化、应变率效应以及绝热影响的相互耦合关系。

3 JC-CS模型的有限元应用

3.1 ABAQUS软件的UMAT二次开发

本文采用UMAT用户子程序接口导入JC-CS本构模型，克服ABAQUS原有材料库中动态本构模型应用范围小的缺点，可适用于宽应变率下的结构塑性变形有限元模拟，提高计算准确性。为实现JC-CS模型的UMAT子程序计算，在应力应变的更新算法上选用径向返回的隐式更新方法[16]，其采用基于Von Mises屈服面的J2流动理论，塑性流动方向始终保持在径向，更新过程无塑性应变和内变量的残量。同时假设塑性流动不受静水压力影响，根据应力偏量来定义流动方向和屈服条件，因此尤其适用于金属塑性的相关计算。根据材料的变形情况将计算流程分为3个部分：弹性阶段应力响应、塑性阶段应力响应以及雅克比矩阵的更新。弹性阶段采用广义胡克定律进行定义，满足初始屈服条件后计算进入塑性阶段。通过计算弹性试探应力σtr，再根据径向返回原理(图6)，当试探应力值超出当前屈服表面时，通过减去塑性校正量回到当前屈服面，从而得到真实应力值，即σ=σtr-3GΔεp，式中G为拉梅常数，Δεp为等效塑性应变增量通过Newton迭代进行求解。在迭代过程中考虑硬化条件即JC-CS本构关系更新屈服应力，同时引入硬化系数对等效塑性应变增量进行计算：

图6 径向返回法示意图

(8)

(9)

式中,Ep为硬化系数;σs为本构模型计算的后继屈服应力。雅克比矩阵的更新参考文献[16]进行编写。更新后的结果存储于ABAQUS提供的依赖于结果的状态变量中，用于下一次的迭代。UMAT子程序计算流程如图7所示。

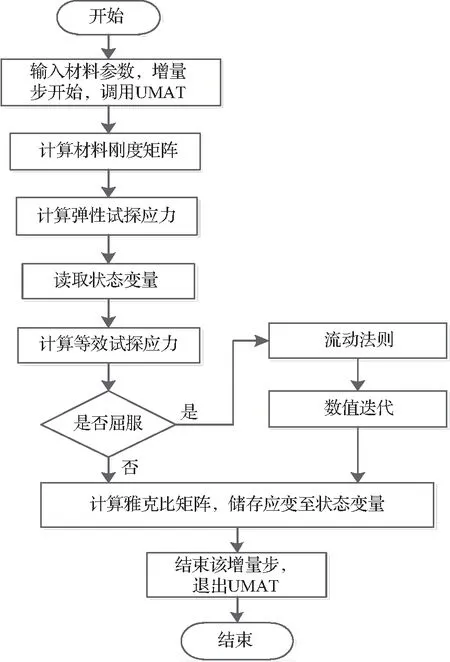
图7 UMAT子程序计算流程

3.2 JC-CS模型与XFEM的结合应用

含初始裂纹的金属在遭受动荷载作用时，往往会产生裂纹扩展。采用传统有限元方法进行结构动态裂纹扩展分析时，需根据裂纹的开展对网格进行重构，计算量非常大。扩展有限元(XFEM)[17]解决了传统有限元的弊端，其采用扩充形函数精确描述与网格无关的间断，在模拟裂纹扩展上不仅能够改善精度，还能大大降低计算成本，受到了广大学者的青睐[3]。在ABAQUS中，XFEM模块只能在ABAQUS/Standard环境中展开计算，且动态下采用XFEM进行裂纹扩展模拟也需要材料动态本构关系为基础，而传统动态模拟大都将本构模型导入ABAQUS/Explicit中。基于此，本文将通过上述二次开发在ABAQUS/Standard中进行JC-CS本构模型与XFEM结合的拓展应用。

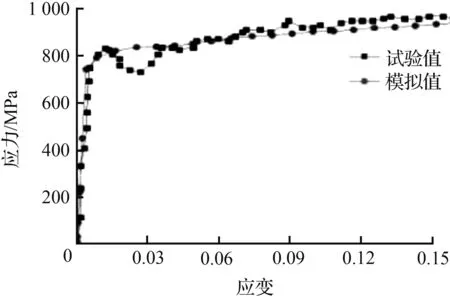
为验证UMAT子程序的正确性，对20CrMnTi钢在不同应变率下的动态流变行为进行研究。模拟采用如图8所示的霍普金森压杆模型(SHPB)，模型尺寸和材料属性参考文献[14]。通过在入射杆杆端设置幅值荷载模拟试验撞击荷载，并加以调整得到相应的应变率时程曲线如图9所示，进一步得到的本构曲线与试验对比如图10所示。

(a) 几何模型

(a) 应变率1 500 s-1

由图10可见，通过有限元计算得到的本构曲线在不同应变率下均与试验值拟合程度较高，说明JC-CS模型的基本参数适用于20CrMnTi钢动荷载下的进一步研究，同时也验证了UMAT子程序的正确性和有效性。

下面进行金属材料动态裂纹扩展分析。20CrMnTi钢三点弯曲梁计算模型如图11所示。加载形式为正弦荷载，波形取半个正弦波，幅值为44 kN，作用时长为80 μs。裂纹萌生的开裂准则采用最大主应力准则，损伤演化采用基于能量的幂法则。分别讨论初始裂纹长度和初始裂纹位置的影响。工况一：设置梁跨中初始裂纹e=0 mm，长度为①a=2 mm；②a=5 mm；③a=8 mm。工况二：初始裂纹设置在梁的不同位置，①跨中e=0 mm；②偏离跨中e=4 mm；③偏离跨中e=7 mm；初始裂纹长度均为a=7 mm。8 mm初始裂纹尖端单元应变率-时间曲线、工况一、工况二裂纹扩展状态图分别如图12至图14所示。

图11 三点弯曲梁计算模型

图12 8 mm初始裂纹尖端单元应变率-时间曲线

(a) 跨中裂纹a=2 mm, e=0 mm

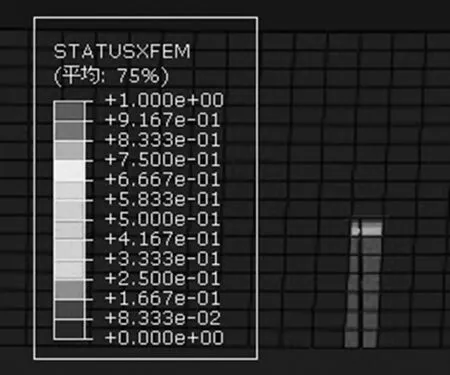
(a) 跨中裂纹a=7 mm, e=0 mm

图12中的ER11、ER22、ER33分别对应整体坐标系XYZ三个轴向的应变率。由图12可知，在半个正弦波荷载条件下，应变率的变化比较复杂，没有明显的规律，也没有稳定的数值，出现的应变率负值是因为不仅存在拉应变还有压应变。整体应变率变化范围较大，涵盖了低中高三个应变率阶段，因此采用宽应变率动态本构方程进行研究较为合理。

由图13中工况一的裂纹扩展状态可以看出，裂纹均沿着竖直方向进行扩展，符合三点弯曲梁跨中位置主拉应力沿水平方向的应力状态，成I型裂纹[17]，同时初始裂纹的长度影响了裂纹的扩展程度，初始裂纹越长，裂纹扩展越深。图14所示工况二中偏裂纹对裂纹的开裂程度影响不大，但是在开裂方向有了较明显的差异，图14(b)、(c)两种情况下裂纹均出现了倾斜，并且偏离跨中位置越大，倾斜角度越大，开裂方向均朝着荷载作用的方向，整体表现出较明显的复合裂纹扩展的特征。

4 结论

本文通过对JC、CS两种常用金属动态本构模型进行宽应变率下的适用性讨论，提出了同时考虑宽应变率效应与温度软化影响的JC-CS模型，并结合20CrMnTi钢、Q420钢和Ti-6Al-4V钛合金三种金属材料在不同加载速率下的实验数据进行金属动态力学特性分析以及三种本构方程的准确性评估。利用UMAT子程序，将JC-CS模型导入ABAQUS进行二次开发应用，通过已有文献验证了UMAT子程序的有效性以及JC-CS模型预测的准确性。

宽应变率下的动态本构模型研究表明：金属材料在高中低各应变率范围内均可能产生明显的应变率强化效应，本文提出的JC-CS模型能准确反映金属应变硬化、应变率效应以及绝热温升影响的相互耦合关系，适用于多金属宽应变范围内的动态本构关系预测，且具有较高的精度。

基于JC-CS模型，结合扩展有限元，通过有限元软件ABAQUS进行了不同初始裂纹下的金属动态裂纹扩展模拟分析，研究表明：动态正弦荷载作用下，金属处于宽应变率范围的受力和变形，基于宽应变率本构关系进行相关研究更为合理；三点弯曲梁模拟试验结果，符合断裂力学规律，只有跨中裂纹时，初始裂纹越长，开裂程度越深，初始偏裂纹的裂纹扩展规律与复合型裂纹相对应。本文的研究成果可以为预测含裂缝的金属材料构件在动力荷载作用下的裂缝扩展规律提供参考。