零售商公平关切对双回收渠道闭环供应链决策的影响
张 涛,张玉豪
(1.上海财经大学信息管理与工程学院,上海 200433;2.上海财经大学上海市金融信息技术研究重点实验室,上海 200433)
环境污染和资源短缺已成为世界范围内急需应对的难题。许多国家制定了相关法律要求企业对其废旧产品进行回收和再制造利用。近些年,闭环供应链愈发受到包括政府,工业界和学术界的重视并得到了迅速发展。企业通过回收和再制造过程不仅能节约资源和保护环境,而且可节约生产成本,创造更多利润[1]。许多著名公司实施了闭环供应链并取得了显著成果。例如Kodak、HP、Xerox和Apple等企业。研究表明企业实施闭环供应链可节约40%~65%的生产成本[2]。
逆向回收渠道选择是闭环供应链管理的研究重点。Savaskan等[3]首先提出了制造商的3种单渠道回收模式,发现零售商进行废旧产品回收时的回收效率最高。之后,众多学者对文献[3]进行了拓展研究。易余胤等[4]研究了需求不确定情景下一个制造商和两个零售商组成的闭环供应链中3种单回收渠道模型的最优决策和绩效的影响。基于不同渠道权力结构,Choi等[5]研究了第三方回收的闭环供应链模型,结果发现零售商主导下的闭环供应链系统效率最高。Zheng等[6]分析了双渠道闭环供应链环境下各渠道成员的最优定价和回收策略。以上文献仅涉及单回收渠道的最优决策问题,均未涉及双回收渠道情景。
在商业实践中,由于单回收渠道的回收效率通常偏低。因此,一些企业采用双回收渠道模式进行废旧产品回收。例如Xerox、Canon和HP等公司在自身进行废旧产品回收的同时,并委托其下游的零售商进行废旧产品回收活动(MR模型)。Kodak公司在自身回收废旧相机时,同时委托第三方回收机构进行废旧相机回收(MC模型)。此外,美国最大的废旧手机制造商ReCelluar公司同时委托其零售商和第三回收方进行废旧手机回收(RC模型)。Hong等[7]系统对比了3种不同双回收渠道模型的最优策略和各渠道成员的利润。较多文献表明企业采取双回收渠道模式优于单回收渠道模式[8-9]。以上文献虽然研究了双回收渠道闭环供应链,但均未考虑渠道成员的运作行为且忽略了商业运营中的需求不确定问题。鉴于此,本文所建模型假设需求为不确定情景以使模型更加贴近现实。
大量行为经济学实证研究表明,人们在决策中是关注公平的,即不仅关注自身收益,而且关注周围其他人的收益情况从而表现出公平关切倾向[10],如最后通牒博弈、信任博弈等。尤其处于弱势地位的决策者更加关注收益的公平分配,当其利润大于利润参考点时处于有利不公平状态,当其利润小于利润参考点时处于不利不公平状态。公平关切的决策者是有限理性的且以追求自身效用最大化为目标,当其感受到不公平待遇时甚至会牺牲自身利益去追求收益分配的公平感知[11]。近些年,一些学者将公平关切纳入到供应链中进行研究。Cui等[12]研究了一个两级供应链中零售商的公平关切行为对渠道协调的影响,并指出制造商可利用一个高于产品边际成本的批发价格契约实现供应链协调。杜少甫等[13]简化了文献[12]中的公平关切效用函数,并探讨了零售商的公平关切行为对批发价格契约,收益共享契约和回购契约的影响。Yang等[14]分析了零售商的公平关切对渠道成员间合作广告效应的影响。Li等[15]基于双渠道供应链环境,分析了公平关切型零售商提供增值服务的最优决策模型。然而,上述文献均未考虑渠道成员的公平关切行为对闭环供应链系统的影响。
由于闭环供应链中渠道成员间的利益竞争更加复杂,从而更容易触发公平关切倾向。因此,将公平关切纳入到闭环供应链中具有很强的理论和实践意义。丁雪峰等[16]考虑了零售商的公平关切行为对闭环供应链最优定价和渠道协调的影响。张克勇等[17]构建了制造商考虑和不考虑零售商公平关切的两种差别定价决策模型。邹清明等[18]将公平关切行为引入到双渠道闭环供应链中,重点分析了零售商的公平关切偏好对渠道成员利润的影响。Zheng等[19]运用合作和非合作博弈理论分析了零售商公平关切对集中决策和分散决策模型的影响。尽管较多学者探讨了渠道成员的公平关切行为对闭环供应链决策的影响,但研究主要集中在单回收渠道闭环供应链,并未考虑双回收渠道闭环供应链情景。
本文针对现有文献的研究不足,建立了需求不确定下具零售商公平关切行为的3种双回收渠道闭环供应链模型。重点探讨了零售商的公平关切行为对3种双回收渠道模型的最优定价,逆向渠道回收率和渠道成员绩效水平的影响,并对不同决策模型中各最优决策变量和绩效水平进行对比分析,以期得到相关管理启示。
1 问题描述与假设
1.1 问题描述
本文研究了由一个制造商,一个公平关切型零售商或和一个第三回收方组成的闭环供应链。制造商采用双回收渠道模式进行废旧产品的回收活动。根据制造商回收渠道选择不同,双回收渠道模式包括制造商和零售商进行回收(MR模型),制造商和第三方进行回收(MC模型)以及零售商和第三方进行回收(RC模型)。制造商不仅利用原材料生产新产品,而且利用废旧产品进行再制造过程。零售商销售新产品且可进行废旧产品回收,第三方负责废旧产品的回收活动。在3种决策模型中,制造商通常拥有较强的渠道势力,为主导者,零售商和第三方为跟随者,故闭环供应链中渠道成员的决策为完全信息下的Stackelberg博弈过程。3种双回收渠道结构如图1所示。图中黑色实线表示正向供应链,黑色虚线表示逆向供应链。由于制造商和第三方均为公平中性决策者,故其期望利润等于期望效用。
1.2 符号说明
模型参数:
φ为市场潜在需求。q为零售商的订购量。β为价格敏感系数。cm为单位新产品的生产成本。cr为单位再制造产品的生产成本。ε为需求随机扰动项。λ为零售商的公平关切系数,λ>0。Δ为单位再制造产品节约成本,Δ≥b>0。B为废旧产品的回收规模参数。E()为渠道成员的期望利润,其中i∈{m,r,c}分别表示制造商,零售商和第三方;j∈{MR,MC,RC}分别表示MR模型,MC模型,RC模型。Ur为零售商的期望效用。s为单位产品的缺货成本。v为未销售单位产品的净残值。
决策变量:
w为单位产品的批发价格。p为单位产品的销售价格。b为制造商对单位废旧产品的回收转移价格。τi为渠道成员的废旧产品回收率。
1.3 模型假设
本文的模型假设如下:
(1)市场需求是随机的,ε为需求随机参数且符合均匀分布,即ε~[-A,A],A<φ。另外,需求函数采用一般线性函数,则有D=φ-βp+ε,φ>βp[4,20]。
(2)制造商和第三方为公平中性决策者,而零售商具有公平关切倾向,其公平关切系数为λ。当λ=0时,零售商无公平关切倾向,当λ>0时,零售商存在公平关切倾向;λ越大表示零售商的公平关切程度越强[13,19]。
(3)本文采用文献[13]中的公平关切效用方程,Ur=πr-λ(π-πr),其中π为零售商的公平利润参考点。当零售商的期望利润小于公平利润参考点时,其效用减少;而当零售商的期望利润大于公平利润参考点时,其效用增加。此外,零售商对单位效用减少和增加的敏感系数相同。
(4)新产品和再制造品的性能和价格相同,即消费者购买两种类型产品的效用相同[3,8]。
(5)零售商的订购量为q,q=φ-βp。当零售商的订购量小于市场需求时,其单位产品的缺货成本为s。当零售商的订购量大于市场需求时,剩余单位产品的净残值为v,v<w。
(6)回收渠道的回收成本是废旧产品回收率的二次函数,即单位回收成本的边际效用是递减的,则有I=Bτ2[1,3]。
(7)为保证各模型存在唯一的最优均衡解,假设B>βΔ2成立,即表明废旧产品回收难度较大,这与实际情况相符[3,5,8]。
(8)各渠道成员对模型参数和变量具有完全信息[1,15,19]。
2 模型分析
本节主要建立上述3种双回收渠道闭环供应链模型并运用逆序求解法得到各模型的最优均衡解。在制造商主导的Stackelberg博弈模型中,各渠道成员追求自身期望利润或期望效用最大化。在决策过程中,零售商根据自身在渠道中的综合实力和贡献程度来选取其公平利润参考点。
2.1 MR模型
本小节建立了制造商和零售商双回收渠道模型。公平关切型零售商在决策时会考虑其所在渠道的利润分配情况,即零售商的公平利润参考点为制造商在正向供应链中的产品批发利润和从零售商进行废旧产品回收的再制造成本节约的总和。模型的决策顺序如下:
(1)制造商首先决定最优批发价格wMR,逆向渠道回收率τMRm和单位回收转移价格bMR
(2)零售商在参考制造商策略的基础上确定最优零售价格pMR和逆向渠道回收率τMRr
根据以上条件可得零售商的期望利润方程为
零售商的公平利润参考点为
则零售商的期望效用方程为
制造商的期望利润方程为

运用逆序归纳法可得MR模型的最优均衡解。
命题1当B>βΔ2时,MR模型存在唯一的最优均衡解如下:

式中:F1=-4B(1+λ)(1+3λ)+βΔ2(1+5λ(1+λ));F2=4B(1+λ)-βΔ2(2+3λ);F3=βΔ2(3+4λ)-6B(1+λ)。
证明:零售商期望效用方程UMRr关于pMR和τMRr的海塞矩阵为

观察上述矩阵,其一阶主子式小于零,矩阵的行列 式 为 |HMRr|=β(4B(1+λ)2-β(b+2bλ-Δλ)2)>0。因此,是pMR和τMRr的联合凹函数。令,可得零售商的最优反应函数为


式(7)、(8)中:F5=A(1+λ)-4(wβ+2wβλ+φ+λφ)+4βλcm;F6=A-4wβ+Aλ-8wβλ+4φ+4λφ+4βλcm。
将公式(7)和(8)代入E(πMRm)中并求其关于wMR和τMRm的海塞矩阵为

式中:F7=-4B(1+λ)2+β(b+2bλ-Δλ)2;F8=-32B(1+λ)(β+2βλ)+8β2Δ(1+2λ)(b+2bλ-Δλ);F9=4B(1+λ)+βΔ(Δλ-b(1+2λ))。
经计算可知,上述海塞矩阵的一阶主子式小于零,矩阵行列式的表达式为
表明E(πMRm)是wMR和τMRm的联合凹函数,其中F10=-4B(-2+Δ)(1+λ)2+βΔ(b+2bλ-Δλ)(-2+b+2bλ-(2+Δ)λ);F11=-4B(1+λ)+βΔ(b+2bλ-Δλ)。

式(10)、(11)中:F12=β(-2bΔ(1+2λ)2+(b+2bλ)2+Δ2(-1-λ+λ2));F13=-4B(1+4λ+3λ2)+β(Δ2λ(1+λ)+(b+2bλ)2)。
将公式(7)、(8)、(10)和(11)代入E(πMRm)中并求其关于bMR的一阶导数得
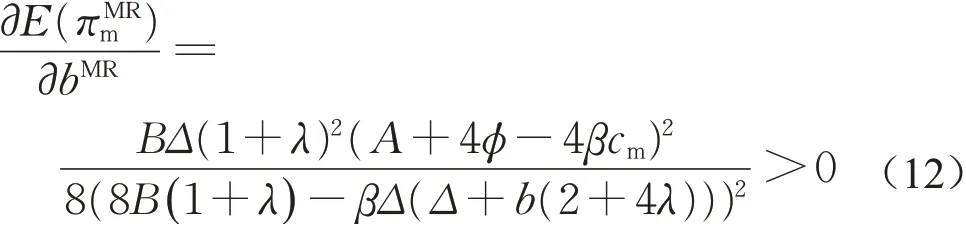
可知制造商的单位回收转移价格越高,其期望利润越大,故最优单位回收转移价格为bMR=Δ。将bMR=Δ分别代入公式(7)、(8)、(10)和(11)中可得MR模型的最优均衡解,继而可得MR模型中各渠道成员的期望效用。
命题2MR模型中的最优批发和零售价格是零售商公平关切系数的单调减函数,制造商和零售商的最优逆向渠道回收率是其单调增函数。

式中:F14=8BβΔ2(1+λ)(3+4λ)+β2Δ4(5+2λ(7+5λ))。
命题2表明当零售商的公平关切行为会降低产品的批发和零售价格。在Stackelberg博弈过程中,零售商的公平关切程度越高,其与制造商讨价还价的能力越强。此时,制造商为了销售更多的新产品从而降低批发价格,同时零售商会适当降低产品销售价格以扩大市场需求,进而激励制造商和零售商提高回收努力水平,故其逆向渠道回收率上升。在此模型中,零售商的公平关切行为对制造商的最优单位回收价格无影响。
2.2 MC模型
本小节建立了制造商和第三方双回收渠道模型。由于此模型中零售商不参与逆向供应链的废旧产品回收活动,故其公平利润参考点仅为制造商在正向供应链中的产品批发利润。此模型的决策顺序如下:
(1)制造商首先决定自身的最优批发价格wMC,渠道回收率τMCm和单位回收转移价格bMC。
(2)基于制造商的决策信息,零售商确定其最优零售价格pMC,第三方确定其最优渠道回收率τMCc。
根据以上条件,可得零售商的期望利润方程为

零售商的公平利润参考点为

零售商的期望效用方程为

第三方的期望利润方程为

制造商的期望利润方程为

运用逆序归纳法可得MC模型的最优均衡解。
命题3当B>βΔ2时,MC模型存在唯一的最优均衡解如下:

式中:F15=3βΔ2λ(1+2λ)-8B(1+λ)(1+3λ);F16=8B(1+λ)-3βΔ2(1+2λ);F17=3φ(-4B(1+λ)+βΔ2(1+2λ))。
证明:零售商期望效用方程UMCr关于pMC二阶导数为,这表明是pMC的严格凹函数。第三方期望利润方程E(πMCc)关于τMCc的二阶导数为,这表明E(πMCc)是τMCc的严格凹函数。令0可得零售商和第三方的最优反应函数分别为



将公式(20)和(21)代入制造商的期望利润方程E(πMCm)中并求其关于wMC和τMCm的海塞矩阵为


表明E(πMCm)是wMC和τMCm的联合凹函数。令可得制造商的最优反应函数为

式(23)、(24)中:F18=(1+λ)(4B(1+λ)+β(2b2-2bΔ-Δ2)(1+2λ);F19=βλ(2b2-2bΔ-Δ2)(1+2λ)+4B(1+4λ+3λ2)。
将公式(20)、(21)、(23)和(24)代入到E(πMCm)中并求其关于bMC的一阶导数得

命题4最优批发和零售价格是零售商公平关切系数的单调减函数;制造商和第三方的逆向渠道回收率是其单调增函数。

式中:F20=48BβΔ2(1+λ)(1+2λ)+9Δ4(β+2βλ)2。
命题4表明在MC模型中,零售商的公平关切程度越强,产品的批发和零售价格越低,同时制造商和第三方的逆向渠道回收率越高。因此,零售商的公平偏好倾向会驱使制造商降低产品批发价格,这可提高零售商的边际利润,从而促进渠道利润分配的相对公平。因此,零售商的公平关切行为是其获得更多渠道利润的一种有效手段。零售价格降低会刺激产品市场需求,制造商和第三方均会增加逆向渠道回收投资,故废旧产品回收率会上升。在此模型中,制造商的最优单位回收价格与零售商的公平关切行为无关。
2.3 RC模型
本小节建立了零售商和第三方双回收渠道模型。此时零售商的公平利润参考点与其在MR模型中的公平利润参考点相同,即制造商在正向供应链的产品销售利润和从零售商回收的废旧产品进行再制造成本节约的总和。此模型的决策顺序如下:
(1)制造商首先决定自身的最优批发价格wRC和单位回收转移价格bRC
(2)根据制造商的决策信息,零售商制定自身的最优的零售价格pRC和逆向渠道回收率τRCr;第三方确定自身的最优逆向渠道回收率τRCc。
根据以上条件,可知零售商的期望利润方程为

零售商的公平利润参考点为

零售商的期望效用方程为

第三方的期望效用方程为

制造商的期望利润方程为

运用逆序归纳法可得RC模型的最优均衡解。
命题5当B>βΔ2时,RC模型存在唯一的最优均衡解为
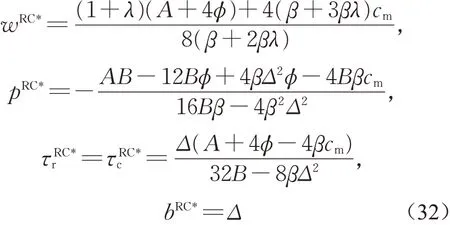
证明:此模型中,零售商期望效用方程URCr的海塞矩阵与MR模型中的公式(8)相同,可知URCr是pRC和τRCr的联合凹函数。由于0,故E(πRCc)是τRCc的凹函数。令可得零售商和第三方的最优反应函数为

式(33)~(35)中:F21=A(1+λ)-4(wβ+2wβλ+φ+λφ)+4βλcm;F22=A-4wβ+Aλ-8wβλ+4φ+4λφ+4βλcm。
将公式(33)~(35)代入E(πRCm)中并求其关于wRC的二阶导数得

表明E(πRCm)是wRC的凹函数,其中F23=bβ(b-2Δ)+β(2b2-4bΔ+Δ2)λ+4B(1+λ)。

式中:F24=β(Δ2λ(2+3λ)-2bΔ(2+7λ+6λ2)+b2(3+10λ+8λ2));F25=4β(βΔ2λ2-b2β(1+2λ)-2bβΔλ(1+2λ)+4B(1+4λ+3λ2))cm;F26=4B(1+λ)+β(Δ2λ+b2(1+2λ)-2b(Δ+2Δλ))。
将公式(33)~(36)代入E(πRCm)中并求其关于bRC的一阶导数得

观察可知,制造商的最优单位回收价格为bRC=Δ。将bRC=Δ分别代入公式(33)~(36)中可得RC模型的最优均衡解,继而可得RC模型中各渠道成员的期望效用。
命题6在RC模型中,产品的最优批发价格是零售商公平关切系数的单调减函数;最优零售价格和逆向渠道回收率均与零售商的公平关切系数无关。


命题6表明,在RC模型中,零售商的公平关切程度越强,产品最优批发价格越低。零售商的零售价格和逆向渠道回收率均与其公平关切倾向无关。此时,零售商为了实现渠道利润分配的公平感知,其需要获取较大的边际利润从而保持零售价格不变,故市场需求量也不会变化。此外,制造商的最优单位回收价格与零售商的公平关切系数无关。由于上述原因使得渠道成员的逆向回收率不受零售商公平关切行为的影响。
3 模型对比分析
本节主要对3种双回收渠道模型的最优均衡解和各渠道成员的绩效水平进行对比分析并得出以下结论(限于篇幅,证明过程省略)。
命题73种双回收渠道模型的最优批发价格和零售价格分别满足wRC*>wMR*>wMC*;当0<λ<时,pMC*>pRC*>pMR*,则DMC*<DRC*<DMR*;当λ>时,pRC*>pMC*>pMR*,则DRC*<DMC*<DMR*。
命题7表明无论零售商的公平关切系数如何变化,制造商的最优批发价格总在RC模型中取得最大值,在MC模型中取得最小值。当零售商的公平关切程度偏弱时,其在MC模型中的零售价格最高,而当零售商的公平关切程度偏强时,其在RC模型中的零售价格最高。此外,零售商的最优零售价格总在MR模型中取得最小值。
命题8τMR*r>τRC*r;τMR*m>τMC*m;τRC*c>τMC*c。
命题8表明制造商和零售商的逆向渠道回收效率MR模型中较高,第三方的逆向渠道回收效率在RC模型中较高。
命题93种决策模型中,制造商的期望利润均与零售商的公平关切系数呈反比。MC模型中第三方的期望利润与零售商的公平关切系数呈正比,而RC模型中其与零售商公平关切系数无关。
命题9表明零售商的公平关切系数越高,制造商的期望利润越低。在MC模型中,零售商的公平关切程度增强会间接提升第三方的逆向渠道回收率,从而使第三方的期望利润增加。在RC模型中,由于制造商的单位回收转移价格和渠道成员的逆向渠道回收率均与零售商的公平关切系数无关,故第三方的期望效用不受零售商公平关切倾向的影响。
命题10①UMRr>UMCr>URCr。②当0<时,当λ>时,E(πMRm)>E(πMCm)>E(πRCm)。 ③E(πRCc)>E(πMCc)。
命题10表明,①无论零售商的公平关切系数如何变化,零售商总在MR模型中取得最大期望效用,而在RC模型中取得最小期望效用,故零售商在MR模型中最为有利。另外,制造商总在MR模型中取得最大期望利润。当零售商的公平关切程度较弱时制造商在MC模型中取得最小期望利润,而零售商的公平关切程度较强时(λ>),制造商在RC模型中取得最小期望利润,故制造商的最优选择为MR模型,即选择自身和零售商双回收渠道最为有利,这也表明零售商的公平关切行为不会改变制造商的最优回收渠道选择。②第三方在RC模型中获取的期望利润大于其在MC模型中的期望利润,故RC模型对第三方最为有利。
命题113种双回收渠道模型的总逆向渠道回收 率 满 足τMR>τRC>τMC,其 中τMR=
命题11表明MR模型的总逆向渠道回收率最高,而MC模型的总回收率最低。从节约资源和环境保护角度看,制造商应选择MR模式回收废旧产品。
命题123种双回收渠道模型的最优单位回收价格满足
命题12表明制造商的最优单位回收价格与零售商的公平关切系数无关。即制造商在制定单位废旧产品回收价格时无需考虑零售商的公平关切倾向。
命题13
命题13表明在3种双回收渠道模型中,市场需求波动幅度越大,产品最优批发价格越高而最优零售价格越低,这会降低零售商的边际利润,但会促进产品市场需求量增加,故各模型的总逆向渠道回收率将上升。
4 数值仿真
本节将利用数值仿真方法对上述结论进行验证并进一步分析零售商的公平关切行为对3种双回收渠道模型最优决策变量和绩效水平的影响,结果见图2~4。根据文献[4,18]的参数设置,令φ=100,β=1,cm=20,Δ=15,A=10,B=800,v=30,s=30,λ∈[0.1,1]。为方便讨论不再考虑各变量和参数的量纲。
由图2a可知,制造商的最优批发价格随零售商的公平关切程度升高而下降且在RC模型中取得最大值而在MC模型中取得最小值。随着零售商的公平偏好程度增强,其与制造商讨价还价的能力越强,制造商为了增加产品销量,从而降低产品的批发价格,这使得零售商可获得更大的边际利润。由图2b可知,MC和MR模型中零售商的零售价格随其公平关切程度增强而降低,而RC模型中零售商的零售价格不受其公平关切行为的影响。此外,当零售商的公平关切程度偏弱时(λ<0.5),MC模型中的零售价格最高;当零售商的公平关切偏强时(λ>0.5),RC模型中的零售价格最高;而MR模型中的产品零售价格始终最低,故制造商选择MR模型时对消费者最为有利。

图2 零售商公平关切系数对不同模型中最优渠道价格的影响Fig.2 Impact of retailer’s fairness concern on channel prices of different models
由图3a、3b可知,制造商和零售商的逆向渠道回收率均随着零售商的公平关切系数增大而上升且在MR模型中取得最大值,这与图3d中MR模型的总逆向渠道回收效率最大相一致。从图3c可知,MC模型中第三方的逆向渠道回收率随零售商公平关切系数的增大有小幅度上升,在RC模型中其不受零售商公平关切系数的影响。由图3d可知,MR和MC模型的总逆向渠道回收率均随零售商公平关切系数的增大而上升,RC模型的总逆向渠道回收率不受零售商公平关切倾向的影响,其原因为在RC模型中,零售商的零售价格与其公平关切程度无关,故零售商的公平关切行为不能间接的对渠道成员的逆向渠道回收努力产生积极影响,故RC模型的总逆向渠道回收率与零售商的公平关切程度无关。

图3 零售商公平关切系数对各渠道成员逆向渠道回收率的影响Fig.3 Impact of retailer’s fairness concern on collection rate of each chain member
由图4a可知,零售商的期望效用随其公平关切系数的增大而增加,这表明零售商的公平关切行为对提高自身效用有利。由图4b可知制造商的期望利润随零售商公平关切系数的增大而减小,即表明零售商的公平关切行为会降低制造商的绩效水平。此时,作为供应链主导者的制造商应采取积极有效的协调措施,避免此种情况发生。由图4c可知,MC模型中零售商的公平关切行为可间接提高第三方的期望利润,但不会影响其在RC模型中的期望利润。由图4d可知,MR模型的总期望效用随零售商的公平关切程度增强而增大,而MC和RC模型的总期望效用均随其增强先减小后增大,其原因主要为在MR模型中,零售商公平关切系数对自身效用的增幅总是大于其对制造商期望利润的减幅,而在MC和RC模型中,当零售商的公平关切系数较小时,制造商期望利润的减幅大于零售商期望效用的增幅,当零售商的公平关切系数大于某一阈值时,零售商期望效用的增幅大于制造商期望利润的减幅,两种模型的总期望效用均会增大。

图4 零售商公平关切系数对各渠道成员绩效水平的影响Fig.4 Impact of retailer’s fairness concern on performance of each chain member
5 结论
本文主要研究了随机需求下零售商的公平关切行为对3种双回收渠道模型的最优决策和绩效水平的影响。通过建模分析和数值仿真得到相关结论和管理启示。零售商的公平关切程度越强,产品的最优批发价格越低,零售价格降低或保持不变,由于MR模型的零售价格最低故此模型对提高消费者剩余最为有利。从环境保护和经济效益角度来看,MR模型的总回收率最高,故制造商选择MR模型对资源节约更为有利。零售商的公平关切行为有利于提高自身期望收益,但会严重损害制造商的期望利润,对第三方的期望利润影响较小或无影响。零售商的公平关切行为对制造商的最优单位废旧产品回收价格无影响。另外,MR模型的总期望效用随着零售商公平关切程度的增强而增大,而MC和RC模型的总期望效用均其增强呈现出先减小后增大的趋势。在商业实践中,零售商的公平关切程度应控制在适当范围内,虽然其能提高自身和闭环供应链的绩效,但会损害制造商的利益,这不利于实现共赢局面,作为领导者的制造商应考虑零售商的运作行为进行综合决策,另一方面,制造商和零售商应加强信息沟通,这有利于减少利益冲突,提高经营绩效。
作者贡献声明:
张 涛:论文建模,写作和修改指导。
张玉豪:论文建模和分析,实验仿真,论文写作和修改。

