不同攻角和翼型的简化角冰特征参数的气动数值模拟
郑诚毅,东乔天,赵宾宾,金时彧,隋冬雨,杨志刚,李伟斌,金哲岩
(1.同济大学航空航天与力学学院,上海 200092;2.中国商用飞机上海飞机设计研究院,上海 201203;3.中国航发商用航空发动机有限责任公司,上海 200241;4.上海地面交通工具风洞中心,上海 201804;5.中国空气动力研究与发展中心,四川绵阳 621000)
在当今所有的飞机事故中,除人为因素外,气象条件导致的事故占所有事故的10%~15%,而气象条件中,结冰对飞行安全的影响最大。近年来随着航空技术的飞速发展,飞机的速度和高度已明显提高,机身防冰、除冰设备也日趋完善,结冰的危害在一定程度上已有所减少。但由于航运交通量的日益扩大,低速飞机(如小型螺旋桨飞机、私人公务机等)的广泛使用,飞机结冰的可能性仍然很大。大型运输机在低速起飞、着陆阶段,或穿越高空的浓密云层时,仍有可能发生严重结冰,并且现有的防冰、除冰设备难以清除程度较重的结冰。飞机部件结冰将恶化飞机的气动特性,使得阻力增大、升力减小,影响飞机的稳定性和操纵性,严重时会致使空难发生。
提高飞机的升力和改进控制面的气动设计可以减少结冰带来的不利影响。有学者指出,准确预测飞机因结冰而导致的空气动力性能退化是结冰分析方法的最终目标之一。为此,需要理解与结冰有关的性能损失,从而改进部件设计。但由于冰形通常比较复杂,具有不可重复性,所以相关数据库的建立需要大量的风洞测试。因此对冰形进行简化,形成一种可以有效预测气动力的可靠的简化冰形是非常重要的。在实验上,简化冰形使得研究人员不需要处理具有有限寿命的真正的积冰;在计算上,它简化了冰形形状的几何建模;简化冰形还可以降低制造难度,降低飞机研发和结冰认证的成本。
角冰(horn-ice)属于明冰(glaze-ice),它的特征可以由高度、高度方向与弦线的角度、表面量纲一长度(s/c,s为冰角所在位置距翼型前缘的距离,c为弦长)等参数来表示。角冰形状通常为具有角状特征的大突起,而决定角冰空气动力学的主要流动特征是角冰下游形成的气流分离区。
针对角冰的气动力性能国内外学者已经做了很多研究。Tani[1]定义了一个气流的长分离区,使其与气流流过角冰产生的分离区相似,结果表明角冰的存在对翼型压力分布具有全局影响。Broeren等[2]使用裂膜风速仪研究了NACA0012翼型覆模拟角冰的5 min平均流场,发现翼型上表面的分离区随着翼型攻角增加而增加,直到气流完全分离。流线分析表明,在各个攻角下,边界层分离点都固定在模拟的角冰尖端附近。Khodadoust[3]研究发现,覆角冰翼型的剪切层过渡点附近湍流强度峰值为0.34,并指出这些数值符合研究的数值范围。此外Eaton等[4]也指出,在气流重新附着点附近的局部湍流强度超过0.30。Gurbacki[5]对机翼前缘角冰后的分离流场做了示意,表明这种流动具有较大的规模,对升力和阻力及其力矩的影响很大。Broeren等[6-7]研究了失速情况下翼型的升力特性,结果表明,随着攻角的增大,气流分离区增大,升力波动也随之增大。国内学者对覆角冰的机翼的气动情况也进行了一定研究。刘娟[8]基于单段翼型过冷大水滴(supercooled large droplet,SLD)的结冰模拟方法发展出适用于三段翼型SLD的结冰模拟方法,并选取了结冰模拟后的角冰冰形进行气动力分析,从流场、压力系数、升力损失等方面进行了分析。李东[9]模拟了400μm和20μm粒径条件下,带舵面的NACA0012翼型在20、40、60 s时的冰型、流线、压力系数及升力系数的变化特征。
角冰冰形简化方面,国内外学者也开展了一些研究。Papadakis等[10-11]用扰流板来代替角冰,不考虑厚度影响,只考虑高度、角度和位置。结果表明,角冰的气动效应并不依赖角冰的具体形状。此外Kim[12]将角冰的下冰角作为研究对象进行试验,发现上冰角主要在攻角较大时增加阻力系数,下冰角在攻角较小或负攻角时影响最大,升力系数则主要和上冰角有关。Olsen等[13]交替添加上下冰角,并进行阻力测量,得到了和Kim类似的结果。此外,在角冰的空气动力学中,粗糙度似乎并没有起到主要作用。Bragg等[14]在研究中发现粗糙度对升力曲线斜率、失速角以及最大升力均无显著影响。
综上所述,附角冰机翼的气动性能基本不受角冰整体形状的影响,而是取决于角冰的高度、角度和位置。由于分离点相对固定在角冰尖端,角冰尖端的形状对气流分离的影响较大,角冰表面粗糙度对气动性能的影响较小。迄今为止,对角冰进行的许多参数化研究只考虑了上角。
本文选定常规翼型NACA23012、自然层流翼型NACA64-215和超临界翼型RAE2822作为对比试验的3种翼型,研究冰角高度、冰角宽度,冰角端部形状以及冰角之间的连接情况4个参数对翼型气动力的影响程度及参数变化产生的气动力变化趋势。
1 数值模拟方法
结冰问题研究常用的湍流模型有Spalart-Allmaras(S-A)模型、re-normalization group(RNG)k-ε模型、realizablek-ε模型、标准k-ε模型等,由于结冰外形千变万化,引起的流动分离现象各有不同,因此各模型都有一定的适用范围。Mortensen[15]比较了不同湍流模型在机翼前缘结冰计算中的精度,结果表明S-A模型在以上几种湍流模型中最优,故本文采用S-A模型进行计算。
为了验证算法的准确性,本文选用Broeren[16]在NACA23012上的EG1164角冰冰形进行算法验证。其中翼型弦长1.828 8 m,计算域取20倍弦长作为半径,马赫数为0.2,雷诺数为1.6×107,攻角为-2°~12°。
数值模拟首先需要选择和验证合适的网格尺度。根据y+等于1的原则,本文将沿着近壁面法向方向的网格厚度取为5×10-6m。选取攻角6°时的试验条件为参考值,得到不同网格点密度下的升力系数平均值,如表1所示。
从表1可以看出,随着网格加密,升力系数的误差保持在千分之一的数量级,综合考虑计算资源,本文选取800×200的网格分布律进行数值计算。角冰的网格如图1所示,网格质量均大于0.7,角度大于18°。
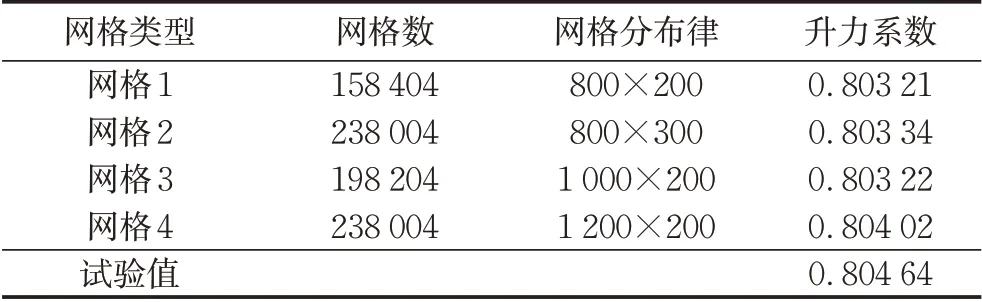
表1 网格与升力系数Tab.1 Mesh and lift coefficient

图1 角冰网格Fig.1 Mesh of horn ice
本文对计算模型进行了验证,相关数据采集自文献[16]。验证结果如图2所示,角冰在未达到失速攻角之前,升力系数和阻力系数的模拟值与文献值误差极小,两者符合得较好。故本文认为采用该数值算法进行带冰翼型的分析计算是有效的。
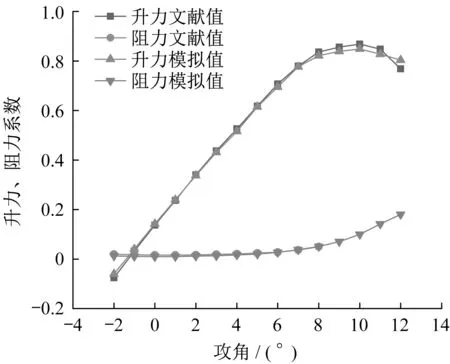
图2 角冰升力、阻力系数文献值和模拟值对比Fig.2 Comparison of simulation value and experi⁃mental value of lift/drag coefficient of horn ice
2 角冰设计参数
本文选取的角冰的简化模型的特征参数分别是冰角高度、冰角宽度、端部形状和冰角之间的连接。冰角高度选择原始高度以及原始高度的±5%;冰角宽度选择原始宽度以及原始宽度的±10%;冰角端部形状有矩形和半圆形;冰角之间连接的特征参数如图3所示。本文选取的计算攻角包含2°、7°和12°。
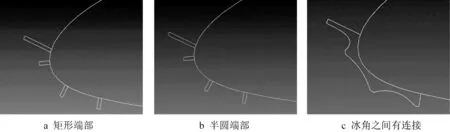
图3 角冰参数示意图Fig.3 Schematic diagram of horn ice parameters
3 不同攻角下NACA23012翼型的数值模拟结果
图4给出了NACA23012翼型分别在2°、7°、12°攻角下,设计的4个角冰参数对升力系数的影响。高于图中标准线值的参数对升力系数有影响,且影响程度随着柱值增大而增大;低于标准线值的参数对升力系数没有影响。从图4中可以看出,冰角宽度在3个攻角下对升力系数均无影响,且权重值随攻角增大而减小。其他3个参数均对升力系数有明显影响,随着攻角变化,对升力系数影响最大的始终是冰角端部形状和冰角之间的连接,冰角高度对升力系数的影响程度略低于其他2个参数。
图5给出了NACA23012翼型分别在2°、7°、12°攻角下,设计的4个角冰参数对升力系数的影响趋势图。从图5可以看出,在3个攻角下,不同参数对升力系数影响趋势相同:升力系数随冰角高度的增加而降低,端部为半圆大于端部为矩形,冰角之间有连接大于无连接。冰角宽度几乎没有影响。即提升简化冰形的升力系数可以选择降低冰角高度,选取圆形冰角端部或添加冰角之间的连接。
图6给出了NACA23012翼型分别在2°、7°、12°攻角下,设计的4个角冰参数对阻力系数的影响权重柱形图。从图6中可以看出,与升力系数类似,冰角宽度在3个攻角下对阻力系数均无影响,且影响程度随攻角增大而减小。其他3个参数均对阻力系数有明显影响:其中起主导作用的是冰角端部形状和冰角之间的连接,在不同攻角下对阻力系数的影响程度始终是最大和次之;冰角高度对阻力系数的影响程度略低于其他2个参数。
图7给出了NACA23012翼型分别在2°、7°、12°攻角下,设计的4个角冰参数对阻力系数的影响趋势图。从图7中可以发现,在3个攻角下,不同参数对阻力系数影响趋势相同,且与对升力系数影响趋势恰好相反,符合实际情况:阻力系数随冰角高度的增加而增加,端部为半圆小于端部为矩形,冰角之间有连接小于无连接;冰角宽度几乎没有影响。即降低简化冰形的阻力系数可以选择降低冰角高度,选取圆形冰角端部或添加冰角之间的连接。
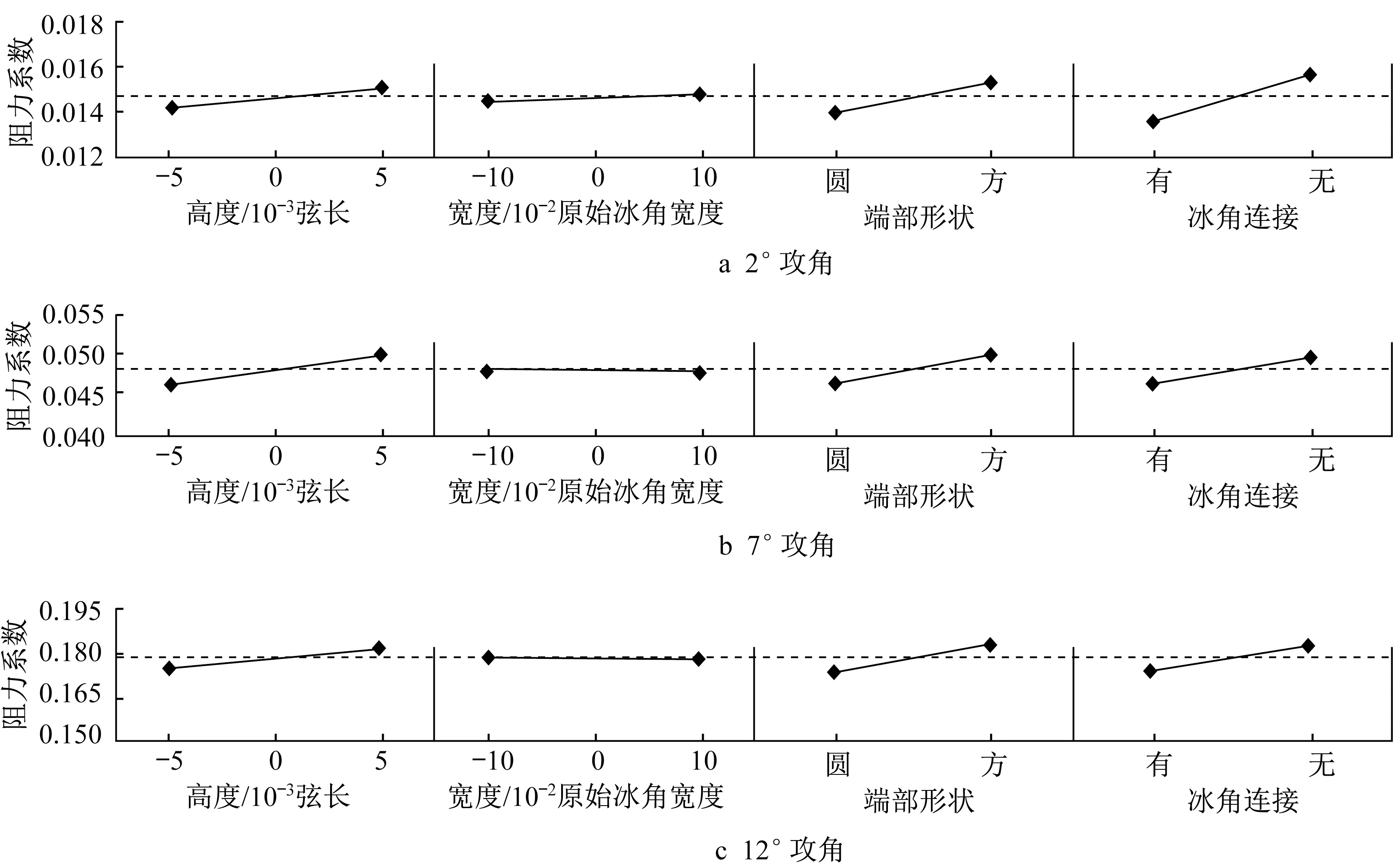
图7 NACA23012翼型的阻力系数趋势分析Fig.7 Trend analysis of drag coefficient of NACA23012
4 不同翼型在2°攻角下的数值模拟结果
图8给出了在2°攻角下NACA23012翼型、NACA64-215翼型和RAE2822翼型的角冰设计参数对升力系数的影响权重柱形图。从图8中可以看出,对于不同翼型,除冰角宽度以外的参数对升力系数的影响主次关系一致,按照影响大小排序为:冰角端部形状、冰角之间的连接和冰角高度。冰角宽度对升力系数没有影响。对于NACA23012翼型来说,冰角之间的连接和冰角高度影响程度相近;而对另外两种翼型来说,起影响作用的3个参数之间有明显的差距。
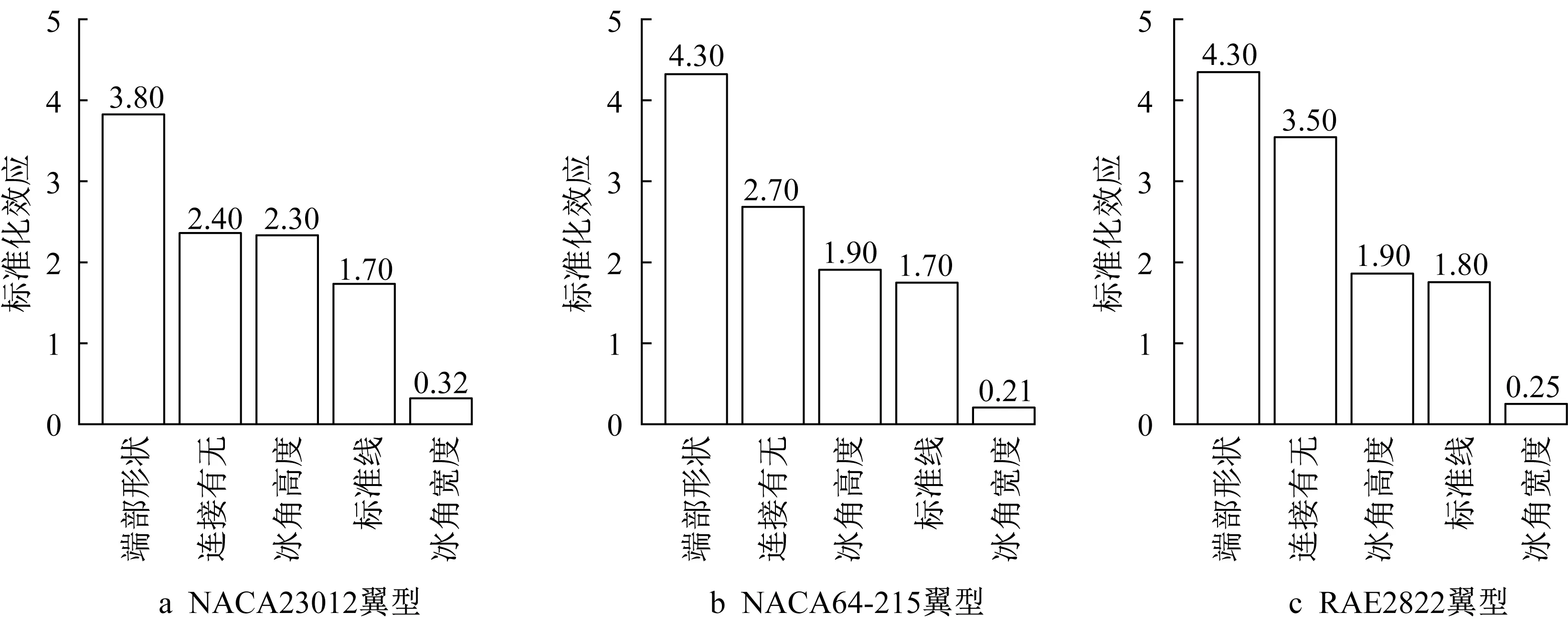
图8 3种不同翼型的升力系数分析Fig.8 Analysis of lift coefficient of three different airfoils
图9给出了在2°攻角下的NACA23012翼型、NACA64-215翼型和RAE2822翼型的角冰设计参数对升力系数的影响趋势图。从图9可以看出,在2°攻角下,对于3种翼型,角冰参数对升力系数的影响趋势一致:升力系数随冰角高度增加而减小,半圆端部大于矩形端部,冰角之间有连接大于无连接。冰角宽度几乎没有影响。即提升简化冰形的升力系数可以选择降低冰角高度,选取圆形冰角端部或添加冰角之间的连接。区别在于同种设计参数对不同翼型升力系数的影响趋势略有不同,这点可以从图中线段的斜率看出。
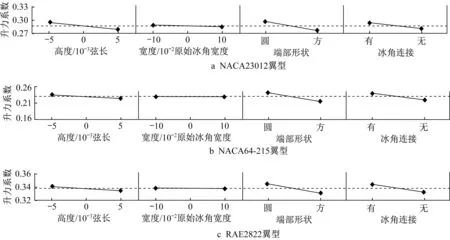
图9 3种不同翼型的升力系数趋势分析Fig.9 Trend analysis of lift coefficient of three different airfoils
图10给出了在2°攻角下的NACA23012翼型、NACA64-215翼型和RAE2822翼型的角冰设计参数对阻力系数的影响权重柱形图。从图10中可以看出,对于NACA23012翼型和RAE2822翼型来说,按照影响大小排序为:冰角之间的连接、冰角端部形状和冰角高度。对于NACA64-215来说,按照影响大小排序为:冰角端部形状、冰角之间的连接和冰角高度,冰角宽度始终没有明显影响。说明不同翼型在2°攻角下的阻力系数对冰角端部形状和冰角之间的连接这2个参数的敏感性不同,在后续的研究中需要分类进行分析。
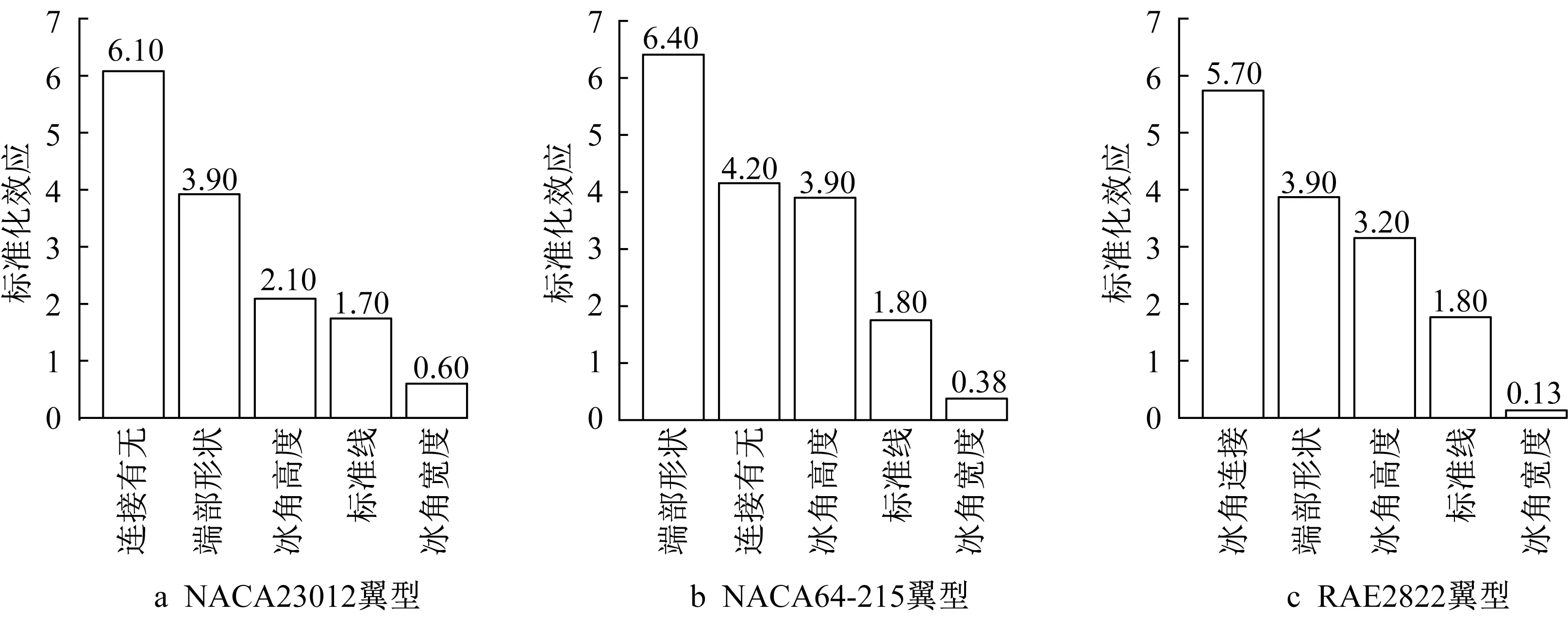
图10 3种不同翼型的阻力系数分析Fig.10 Analysis of drag coefficient of three different airfoils
图11给出了在2°攻角下的NACA23012翼型、NACA64-215翼型和RAE2822翼型的角冰设计参数对阻力系数的影响趋势图。从图11可以看出,在2°攻角下,对于3种翼型,角冰参数对阻力系数的影响趋势一致:阻力系数随冰角高度增加而增加,半圆端部的影响小于矩形端部,冰角之间有连接的影响小于无连接。冰角宽度略微有一些影响,且不同翼型阻力系数对冰角宽度的敏感性不同。与升力系数类似,同种设计参数对不同翼型的阻力系数趋势略有不同,这点可以从图中线段的斜率看出。
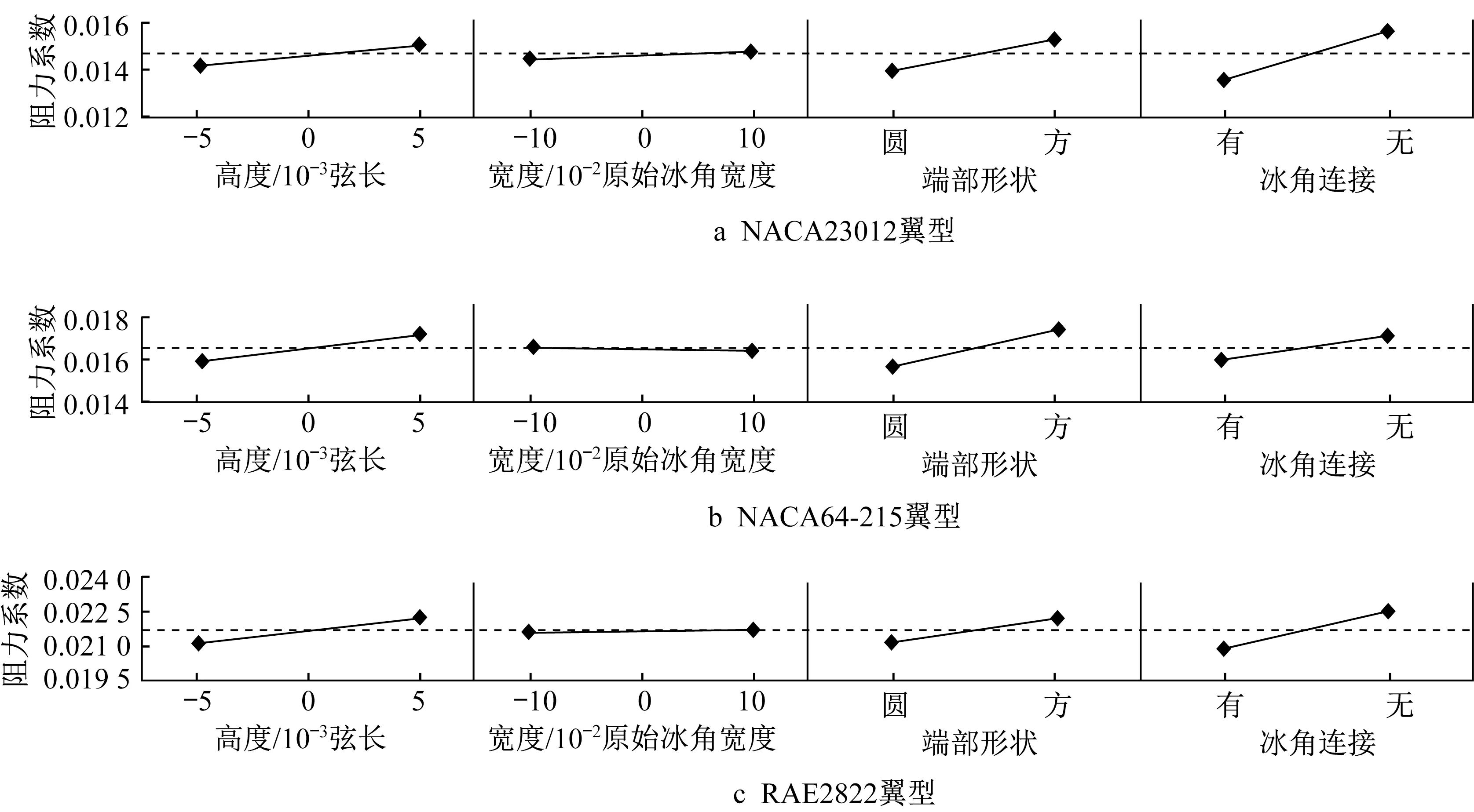
图11 3种不同翼型的阻力系数趋势分析Fig.11 Trend analysis of drag coefficient of three different airfoils
5 结论
本文研究获得了NACA23012翼型在3个攻角带角冰情况下,角冰的4个设计参数对翼型气动力的影响程度和趋势:冰角端部形状和冰角之间的连接对气动力的影响最大,其次是冰角高度,最后是冰角宽度;如需增加翼型带角冰情况下的升力系数,可以通过选择半圆形的冰角形状、增加冰角之间的连接和减小冰角高度来达成;增加阻力系数则相反。通过对比NACA23012翼型、NACA64-215翼型和RAE2822翼型在2°攻角下设计参数对翼型气动力的影响,得到了不同翼型对角冰的设计参数的敏感性不同的结果,说明不同翼型的简化角冰模型需要单独设计。
作者贡献声明:
郑诚毅:数值模拟及撰写论文。
东乔天:网格建模。
赵宾宾:项目背景调研及参考文献的整理。
金时彧:数据处理与分析。
隋冬雨:提供简化冰角的具体方案。
杨志刚:指导ANSYS软件的具体使用。
李伟斌:文献调研及背景分析。
金哲岩:论文的整体规划及具体研究内容的工作安排。

