基于Fluent的生物培养箱温度场分析

张宇驰,刘淑莲,郭刚祥

(1.浙江科技学院 机械与能源工程学院,杭州 310023;2.浙江省计量科学院,杭州 310018)

生物培养箱(以下简称培养箱)作为培养生物生长的重要装置,在生物生长中起到了不可忽视的作用。为了生物的生长过程中保持活性和健康生长,需要培养箱具有稳定的保温效果,箱内温度过高或温差过大均会导致生物生长出现问题。近年来,随着生物技术的发展,培养箱的需求增加,对培养箱内温度的研究逐渐引起人们的重视。许多研究者基于计算流体力学(computational fluid dynamics,CFD)对生物生长环境的温度进行了研究。贾鹤鸣等[1-3]对生物的生长环境进行了温度场仿真,结果与试验结果吻合,这证明了CFD温度场仿真的可靠性,为进一步研究提供了理论和技术支持。随着生物技术的发展,培养箱成为许多实验室的重要设备,被广泛应用于医学[4-5]、微生物[6]、农业科学[7]、药物学[8]的研究和生产,由于温度是培养箱的重要影响因素,故许多研究者对培养箱温度场进行了分析。周峰等[9]对婴儿培养箱设计了9组水平试验进行计算流体动力学仿真,对培养箱内温度场和流场均匀性进行了优化;张京等[10-11]基于CFD软件对CO2培养箱进行仿真分析,研究了CO2培养箱内温度场的变化;宋文龙等[12-15]对植物培养箱进行了温度场仿真,验证了模型的可行性和提高了温度场的均匀性。

研究者多使用Fluent软件对培养箱温度场进行仿真,通过仿真结果改进结构的方法较少,因此,本研究使用CFD仿真研究培养箱温度控制,采用Fluent软件对培养箱结构进行温度场仿真分析并进行改进,分析安装CO2检测模块对温度场的影响,对CO2检测模块进行圆角化优化。

1 培养箱基本结构设计

1.1 有CO2检测模块的培养箱模型

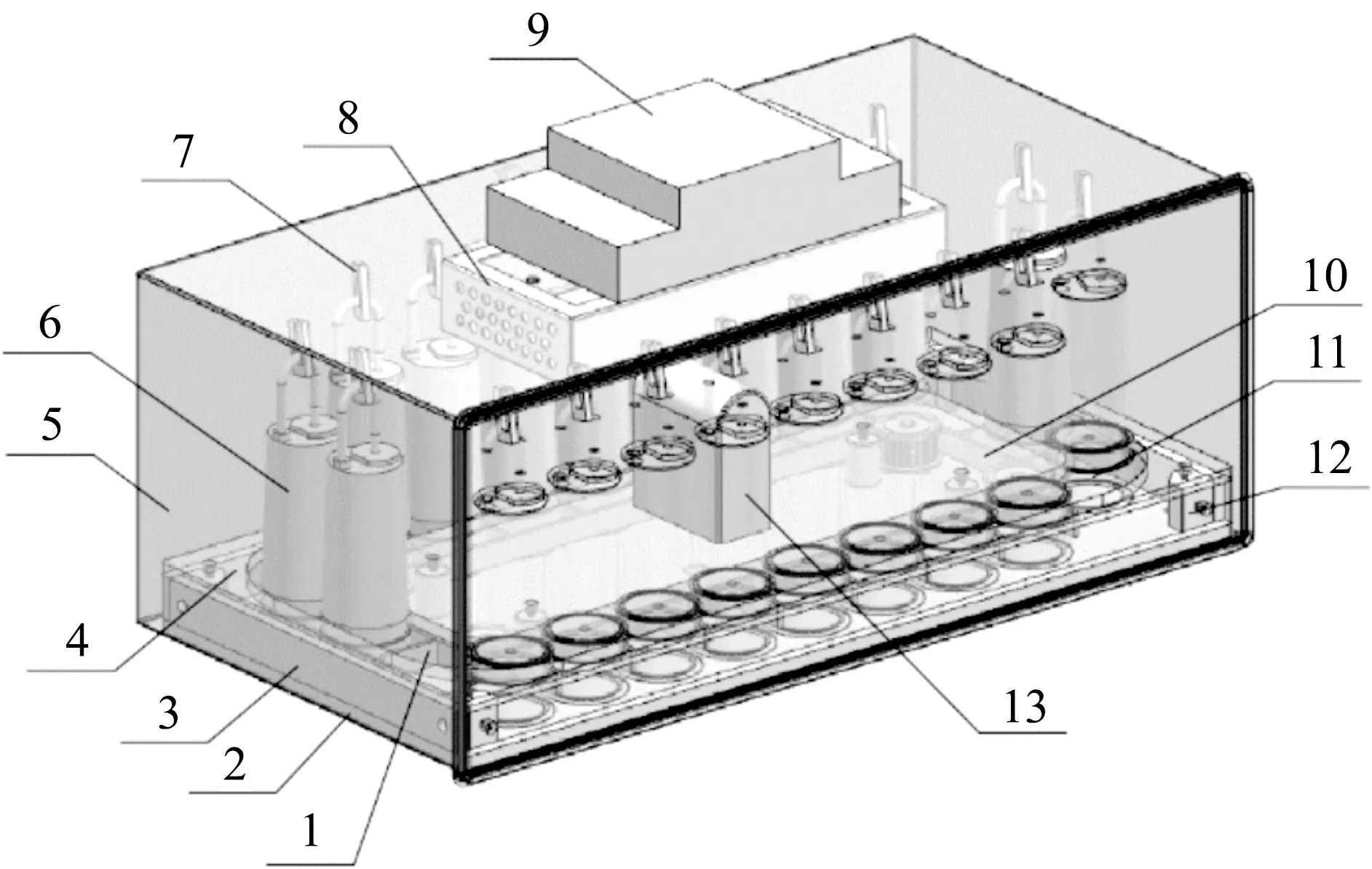
1—同步带;2—下底板;3—支撑板;4—外槽板;5—箱体;6—培养瓶;7—卡扣;8—制冷片罩盖;9—制冷片;10—上底板;11—培养瓶底座;12—定位块;13—CO2检测模块。图1 有CO2检测模块的培养箱模型Fig.1 Incubator with CO2 detection module model

有CO2检测模块的培养箱模型如图1所示,箱体外壳的长、宽、高分别为58、30.5、22 cm,箱体内壁材料为不锈钢,内壁与外壳之间有接近绝热的隔热材料,箱内底部区域由培养器下底板、前后左右支撑板和外槽板构成,通过安装在下底板上的4个定位块定位,同步带带动培养瓶转动,其上方覆盖了上底板,并安装了CO2检测模块。培养箱进出口如图2所示,进口位于制冷片罩盖的下方,出口位于制冷片罩盖的两侧,正前方是前壁面,由玻璃门构成,可打开。培养箱空气流通路线如图3所示,外界空气从制冷片罩盖下方进口以一定的速度流入,进入培养箱之后流经培养瓶等,最后从制冷片罩盖出口流出。持续通入一定温度的空气能保持培养箱内部气体温度分布均匀。

图3 培养箱空气流通路线Fig.3 Air flow route of incubator

1.2 无CO2检测模块和CO2检测模块圆角化的培养箱模型

为了研究CO2检测模块是否对培养箱温差有影响,在有CO2检测模块培养箱模型的基础上,做以下两种调整,一是将CO2检测模块移除,二是将CO2检测模块左右侧面与顶面之间进行半径为18 mm的面倒圆,培养瓶分布和运动方式与原模型相同。无CO2检测模块培养箱模型如图4所示,CO2检测模块圆角化模型如图5所示。

图4 无CO2检测模块的培养箱模型Fig.4 Incubator model with no CO2 detection module

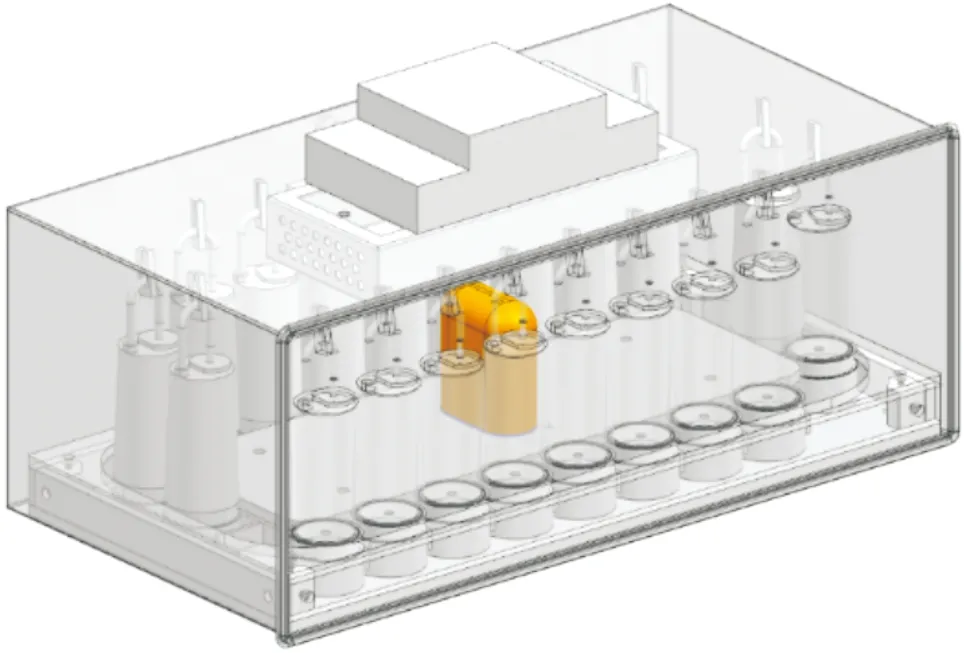
图5 CO2检测模块圆角化的培养箱模型Fig.5 Incubator model with CO2 detection module rounding

1.3 控制方程

进出口和培养箱内部流场同时具有层流、层流向湍流转捩流、完全湍流,培养箱内又有流场的内部循环,所以采用方程转捩的k-kl-ω模型。k-kl-ω模型是一个三方程的涡流-黏性型模型:

(1)

(2)

(3)

式(1)～(3)中:kT为湍流动能;PkT为湍流产生项;R为波动流向旁路过渡时分解为湍流的平均效应;Rnat为湍流破裂,是一个自然过渡生产项;ω为逆湍流时间标度;DT为湍流近壁耗散;v为湍流黏度;αT为湍流标量扩散系数;αk为动能标量扩散系数;αω为逆湍流时间标度标量扩散系数;kL为层流动能;PkL为层流产生项;DL为层流近壁耗散;fω为阻尼;fW为小规模能量;Cω1、Cω2、Cω3、CωR分别为0.44、0.9、0.9、1.5。

2 网格划分及计算条件

2.1 网格划分

培养箱的网格划分采用四面体非结构化网格,为了着重研究培养瓶附近温度,对培养瓶进行网格加密,同时对同步带和传动轮进行加密。培养箱的网格划分如图6所示。

图6 培养箱的网格划分Fig.6 Meshing generation of incubator

2.2 边界条件及收敛性计算

入口设置为速度进口,v=4 m/s,出口边界条件设置为自由流出口,培养瓶等其余部件皆设置为壁面。入口风温度设置为27 ℃,培养瓶温度设置为20 ℃,培养箱内初始温度设置为23.5 ℃。

使用单精度方式求解纳维-斯托克斯方程,动量方程计算采用三阶迎风格式,能量方程计算采用二阶迎风格式,其余方程计算采用一阶迎风格式。

2.3 网格数无关性分析

网格数无关性分析见表1。由表1可知,当网格数为13 487 194时,平均温度为24.228 ℃,与网格数为15 762 036时的平均温度相差0.02 ℃,大约为网格数为15 762 036时平均温度的0.4%;当网格数为17 291 167时,平均温度为24.189 ℃,与网格数为15 762 036时的平均温度相差0.019 ℃,大约为网格数为15 762 036时平均温度的0.38%;而当网格数为17 291 167时,计算机提示“由于网格过多是否显示网格”,即将达到计算机极限值,会过多占用计算机的内存。因此当选择15 762 036这一网格数研究时,既能充分利用计算机的运算能力,又能有足够的网格使计算精确。

表1 网格数无关性分析Table 1 Grid number independence analysis

3 有无CO2检测模块对温度场的影响

3.1 温度场云图分析

培养箱温度总体情况如图7所示,温度在22～27 ℃(295.15～300.15 K)之间,最高点在进口处,总体温度情况为从中心向边缘降低。由于总体图难以看到培养瓶附近的温度变化,故需取截面来观察。在距离箱体底部高度为80 mm处截取截面,观察截面温度云图。有CO2检测模块模型截面温度云图如图8(a)所示,无CO2检测模块模型截面温度云图如图8(b)所示。由图8可知,培养箱温度分布为中间温度高,边缘温度低。相比有CO2检测模块模型的温度云图,无CO2检测模块模型的温度云图在中间培养瓶处无温度降低情况。

图8 模型截面温度云图Fig.8 Cross-sectional temperature cloud diagram of model

3.2 温度场测点选取及分析

为了了解培养瓶附近的温度变化情况,在培养瓶附近选取测点。由于培养箱对称,故取5个培养瓶研究。在每个培养瓶附近取10个测点,前后两个面各取5个测点。培养箱附近测点分布如图9所示,测点分布在面1(橙色面)和面2(蓝色面)上。面1和面2上的测点如图10所示。

图9 培养箱附近测点分布Fig.9 Distribution of measuring points near incubator

图10 面1和面2上的测点Fig.10 Measurement point diagram on face 1 and face 2

测点温度曲线如图11所示,从图中可以看出,无CO2检测模块后,培养瓶1附近测点2处的温度无陡降,且培养瓶1附近的温差有所减小;培养瓶2和培养瓶3附近温差也明显有所减小;培养瓶4附近温度变化微小;培养瓶5处温差有所增大。由此得到,无CO2检测模块时,多数培养瓶附近温差减小,虽有少部分培养瓶附近温差变大,但总体温差有所减小。由于CO2检测模块需安装在培养箱内,故需改进CO2检测模块使培养箱内温差不会因有CO2检测模块而增大。

图11 测点温度曲线Fig.11 Temperature curves of measuring points

4 CO2检测模块圆角化对温度场的影响

为解决有CO2检测模块使培养箱内温差增大的情况,本研究采用CO2检测模块圆角化的方法。

4.1 温度场云图分析

与3.1节取相同截面观察,CO2检测模块圆角化的培养箱模型截面温度云图如图12所示。由图12可知,CO2检测模块圆角化的培养箱模型与有CO2检测模块的培养箱模型和无CO2检测模块的培养箱模型温度分布类似,中间温度高,从中心向边缘温度逐渐降低,但中间培养瓶处温度突变不明显。

图12 CO2检测模块圆角化模型截面温度云图Fig.12 Cross-sectional temperature cloud diagram ofCO2 detection module rounding model

4.2 温度场测点选取与分析

温度场的测点选取方法与3.2节相同。加上CO2检测模块圆角化数据的测点温度曲线如图13所示。由图13可知,CO2检测模块圆角化后,培养瓶1～3附近温差相比原模型(有CO2检测模块)明显减小,与无CO2检测模块的模型温差相差极小;培养瓶4附近温差与有CO2检测模块的原模型和无CO2检测模块模型皆相差极小;培养瓶5附近温差相比原模型略微增大,但明显小于无CO2检测模块。由此可得,CO2检测模块圆角化可以消减有CO2检测模块所带来的温差增大,仅有个别培养瓶附近温度略微大于原模型,可以忽略不计。本研究考虑的是静态情况,由于培养箱内有同步带带动培养瓶转动,所以实际每个培养瓶的温差会比静态时更小。

图13 测点温度曲线Fig.13 Temperature curves of measuring points

5 结 语

本研究对生物培养箱内温度场进行了仿真分析,同时对模型进行了两种方案的改进。培养箱内无CO2检测模块模型相比有CO2检测模块模型在多数培养瓶附近温差有所减小,少数培养瓶附近有所增大;CO2检测模块圆角化培养箱模型在多数培养瓶附近温差相比原设计模型有所减小,少数培养瓶附近温差仅略微增加(可以忽略不计),比无CO2检测模块时温差更小。因此,CO2检测模块圆角化方案最佳。本研究对培养箱结构提出了优化方案且取得了较好的效果,之后可以进一步研究圆角化程度对培养箱温度场分布的影响。