新型冠状病毒肺炎疫情中后期的发展趋势分析——基于意大利疫情数据

姚 艺,钱亚冠,陈晓霞,徐庆华,方科彬

(浙江科技学院 理学院,杭州 310023)

新型冠状病毒肺炎(以下简称新冠肺炎)发生以来,对疫情未来趋势的预测一直是学术界关注的热点。针对此次疫情不少研究者对其展开探讨。Zhao等[1]基于2020年1月10日至24日的公开数据进行指数增长趋势曲线拟合,由此判断新型冠状病毒早期传播能力接近或略高于SARS。倪顺江[2]把复杂网络理论和流行病学研究相结合,建立了传染病动力学模型,试验发现传染病感染人数初期时以指数形式增长。这些研究都认为新冠肺炎初期传播具有指数增长的特点,对判断新冠肺炎初期传播的规模和特点具有重要意义。但传统的曲线拟合完全是基于数据趋势来进行预测,无法考虑传染病的传播速度、传播模式及各种防控措施的实施等动态信息,预测效果在初期过后并不可靠。张琳[3]利用一般增长模型,分3个阶段拟合新冠肺炎确诊人数(初期,无障碍指数增长阶段;中期,次指数增长阶段;后期,次线性增长阶段)。而次指数增长方式的内在机制,主要有空间异质性、群聚感染及感染参数的时间异质性[4]等几方面解释。在SIR(susceptible-infective-removal)模型中,考虑空间异质性[5]、传染率的时变性[6]及异质混合模型[7],都能够呈现出次指数的增长方式。Yang等[8]运用长短期记忆(long-short-term-memory,LSTM)模型预测中国疫情将在2月底达到高峰,并通过机器学习算法展示若取消湖北省的交通封闭措施,将导致湖北省在3月中旬出现第二次高峰。

2020年3月17日,意大利新冠肺炎死亡人数超过武汉[9],成为疫情严重国家。这引起了研究者们的关注。陈晓平[10]通过聚类分析方法研究各国新冠肺炎疫情发展的严重程度,将国外新冠肺炎疫情国家分为主要疫区、重点疫区、分散疫区3类,其中意大利属于主要疫区。刘波[11]认为,意大利新冠肺炎疫情是全球化背景下的集体问题,这场疫情既考验欧盟处理公共突发事件的能力也给欧洲乃至世界产生了深刻而复杂的影响。

现有的新冠肺炎疫情预测方法包括曲线拟合(curve fitting)、传染病动力学模型(epidemic dynamics model)及人工智能算法(artificial-intelligence,AI)三大类[12]。疫情预测的主流算法有改进的传染病动力学模型和LSTM模型[13]。为了更好地预测意大利新冠肺炎各阶段的传播情况,本研究选用logistic(逻辑回归)模型、SIR模型和LSTM模型进行预测。通过对试验结果的分析和对比,提取各模型中有价值的预测信息,取长补短,为此次疫情提供更为全面细致的预测结果。

1 预测模型

1.1 logistic模型

logistic[14]模型是Verhulst-Pear在修正密度方程时提出的,常用于描述种群、传染病增长及商品销售量预测等方面。logistic函数如下:

(1)

式(1)中:P(t)为t时刻的人口数;P0为初始容量;r为人口增长率;K为环境最大容纳量。

使用logistic模型预测的主要步骤如下:

1) 利用最小二乘法构造损失函数:

(2)

式(2):Pt为t时刻实际确诊人数;P(t)为t时刻模型预测的确诊人数。

2) 将损失函数分别对模型参数K、P0、r求导建立方程组,即

求出与真实确诊病例数据最接近的logistic函数:

由上述logistic函数定义可知此次疫情累计确诊病例人数最大会达到268 999人;模型的初始容量P0为22 060人,人口增长率r为0.01。

3) 利用P(t)函数预测在测试集上的确诊病例数,用平均绝对百分比误差[15](mean absolute percentage error,MAPE)指标计算模型精确度。

(3)

式(3)中:Yt为预测值;yt为真实值;n为预测点的个数。

MAPE值大小与预测精度呈反比关系,MAPE值越小,预测越准确。一般情况下,如果MAPE值小于20%,则模型拟合效果好。

由于意大利于2020年5月4日实施解封,导致实际累计病例数在后期仍持续向上增长,而在logistic模型中,人口数在后期达到饱和状态后会维持水平无法向上增长。因此,本研究把数据分成2020年2月21日至5月3日和5月4日至8月18日分别进行拟合,并在两段输入数据里划分训练集和测试集(比例为7∶3)。

1.2 SIR模型

SIR模型是一种仓室模型[16],它将发病地区的所有人分为易感者(Susceptible,S)、感染者(Infective,I)及移出者(Recovered,R)3类,并通过某一群体转移至另一群体的传播学机制来建立常微分方程组,以揭示疫情传播的规律。

模型设置了如下假定:1)冠状病毒通过飞沫直接传播;2)总人口数是一个常数,不发生变化,任何时刻的3类人群总数不变;3)易感者为尚未感染的健康人群;4)感染者是已被感染、具有传染性的人群;5)感染者一段时间之后可以康复,且成为移出者后对于该疾病具有免疫能力。

SIR模型的常微分方程组形式[17]如下:

(4)

式(4)中:β为易感者被传染的平均概率;γ为感染者痊愈的平均速率;t为冠状病毒传播天数;N为人口总数。

(5)

存在。式(4)的第2个方程意味着I(t)的变化依赖S(t)的大小。如果

(6)

那么当t→∞时可以得到I0>I(t)→0,此时疾病将消亡而不会暴发。根据基本再生数理论,定义:

(7)

基本再生数R0[18]是刻画传染病是否会暴发的阈值。当R0<1时,疾病不会暴发,且随时间的推移逐渐消亡;当R0>1时,疾病会暴发一段时期,在达到I(t)最高值后随时间的推移逐渐消亡。同时,我们定义相应的当日再生数为

(8)

式(8)中:S(t)为当日易感者的人群数量;βt为当日的平均传染率;γt为当日的平均恢复系数。

使用SIR模型预测的主要步骤如下:

1) 将输入数据进行规范化处理,输入数据的区间为2020年2月21日至8月18日。

2) 利用最小二乘法构造损失函数:

(9)

式(9)中:I(t)为真实感染者病例数;R(t)为真实抵抗者病例数;It为模型感染者病例数;Rt为模型抵抗者病例数。为了加强模型的拟合效果,损失函数中对确诊病例数的误差项进行了加权,取权重a=9。

3) 将损失函数分别对模型参数β、γ建立方程组,即

以求出一个既满足SIR常微分方程关系又与真实确诊病例数据最接近的SIR曲线,最后求得的SIR模型常微分关系如下:

此时,易感者的平均被传染率βt为0.000 001 29;感染者痊愈的平均速率γt为0.031 408 08。

4) 利用求得的SIR模型常微分关系预测确诊病例数据,用MAPE指标验证模型的准确性。

1.3 LSTM模型

LSTM模型[19]能够对长时间跨度的时间序列保持良好的记忆,该模型在时间序列的预测问题上有着突出的表现。LSTM模型原理是充分利用过去若干天数的数据信息预测未来若干天数的数据。使用LSTM模型进行确诊病例数预测的主要步骤如下:

1) 读取疫情数据,将输入数据进行规范化处理并划分为训练集和测试集,划分时序窗口,设置窗口长度L=3,学习率α=0.005,迭代偏置为0.000 01,最大迭代次数T=2 000;

2) 将输入数据经过输入层的所有节点传递到隐藏层,隐藏层结合Sigmiod激活函数将变量映射到[0,1]之间以决定信息是否向下层传递;

3) 运用tanh函数计算当前状态xt、上一刻LSTM的隐藏层状态ht-1和记忆单元状态ct-1等参数值经过遗忘门叠加处理形成的新记忆单元状态值ct;

4) 利用Sigmoid函数获得初始输出,并利用tanh函数对数据缩放得到预测输出ht;

6) 权重和偏置更新,基于损失函数E使用Adam梯度优化器更新W和b,当更新前后差值的绝对值小于ε时结束循环;

7) 输入测试数据集,验证模型准确性;

8) 运用训练后的LSTM模型对未来确诊人数进行预测,即用历史确诊人数xt,xt+1,…,xt+L-1预测下一时刻的确诊人数pt+L。

2 试验结果分析

2.1 试验数据

试验数据来源于意大利民事保护部门的疫情通报(http://www.salute.gov.it/portale/home.html),时间范围为2020年2月21日至8月18日,包括现存确诊人数、累计确诊人数、死亡人数和治愈人数4个指标,数据质量良好,无缺失值。其中,logistic模型使用的数据为2020年2月21日至8月18日的累计确诊人数;SIR模型使用的数据为2020年2月21日至8月18日的现存确诊人数和治愈人数;LSTM模型使用的数据为2020年2月21日至8月18日的累计确诊人数和现存确诊人数。

2.2 模型精度比较

为了避免试验的偶然性,我们进行了重复试验,取均值作为该模型的MAPE指标值,训练结果见表1。

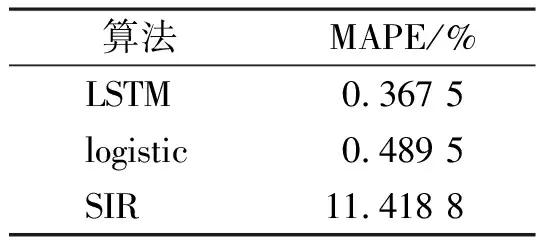
表1 MAPE值比较Table 1 Comparison of MAPE values

从试验结果中可以看到3种模型的MAPE值均远小于20%,即3种模型预测结果均有效。其中,LSTM模型的MAPE值最小,为0.367 5%。3种模型得到的MAPE指标值均非常小,其原因可能是分母实际确诊病例的数值过大。模型SIR的MAPE指标值与其他两种模型相差20倍之多。导致这一差异的原因可能是SIR模型无法将突发的“解封”措施考虑在内,使得预测效果在后期并不理想。而Logistic模型则通过分段预测的方法大大提高了其预测精度。

通过试验发现,Logistic、SIR和LSTM模型在预测中均各有优势与不足。因此,研究者需要综合考虑,提取模型各自最有价值的预测信息以得到更为全面的预测结果,3种模型的优缺点对比见表2。

表2 3种模型的优缺点对比Table 2 Comparison of advantages and disadvantages of three models

2.3 缓增期的模型预测

由logistic模型预测得到的确诊病例数结果如图1所示。红色的虚线为模型感染病例数的预测值,模型预测区间为2020年2月21日至12月15日,蓝色的实线为截至2020年8月18日官方公布的实际数据。

图1 logistic模型累计确诊病例趋势预测Fig.1 Trend prediction of cumulative confirmed cases by Logistic model

根据上文试验分析模型预测在2020年9月29日后疫情进入缓增期,随后确诊病例数继续向上增长,最终的累计确诊人数K会达到268 999人。从图1中可以看出,模型的预测曲线与实际数据的总体增长趋势一致,在疫情后期两者的偏差随着时间节点的推移而逐渐变大。

2.4 当日再生数的模型预测

由SIR模型预测得到的确诊病例数结果如图2所示。在SIR模型中用I类人群拟合实际确诊病例数。I(t)、R(t)为真实的确诊人数和移出者人数;St、It、Rt分别为模型预测的易感者人数、感染者人数和移出者人数。从图2中可以看出,模型预测在2020年4月21日出现拐点,现存感染人数的峰值可达到约124 554人(略高于真实数据)。但在2020年7月10日后,模型预测曲线开始偏离真实数据,可见,在疫情后期SIR模型的预测效果不佳。

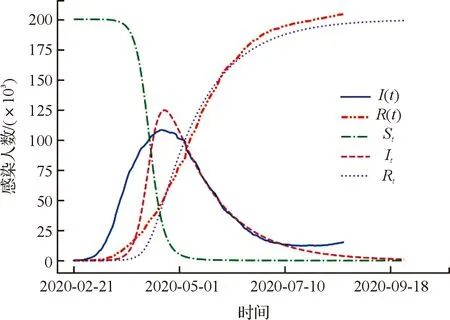
图2 SIR模型现存确诊病例趋势预测Fig.2 Trend prediction of existing confirmedcases by SIR model

以2020年2月11日至3月8日为第一个时间段,每增加一天构成一个新的时间段,用SIR模型求解其当日再生数Rt,得到了当日感染再生数随时间推移的演化趋势图,预测区间为2020年3月8日至7月10日,如图3所示。

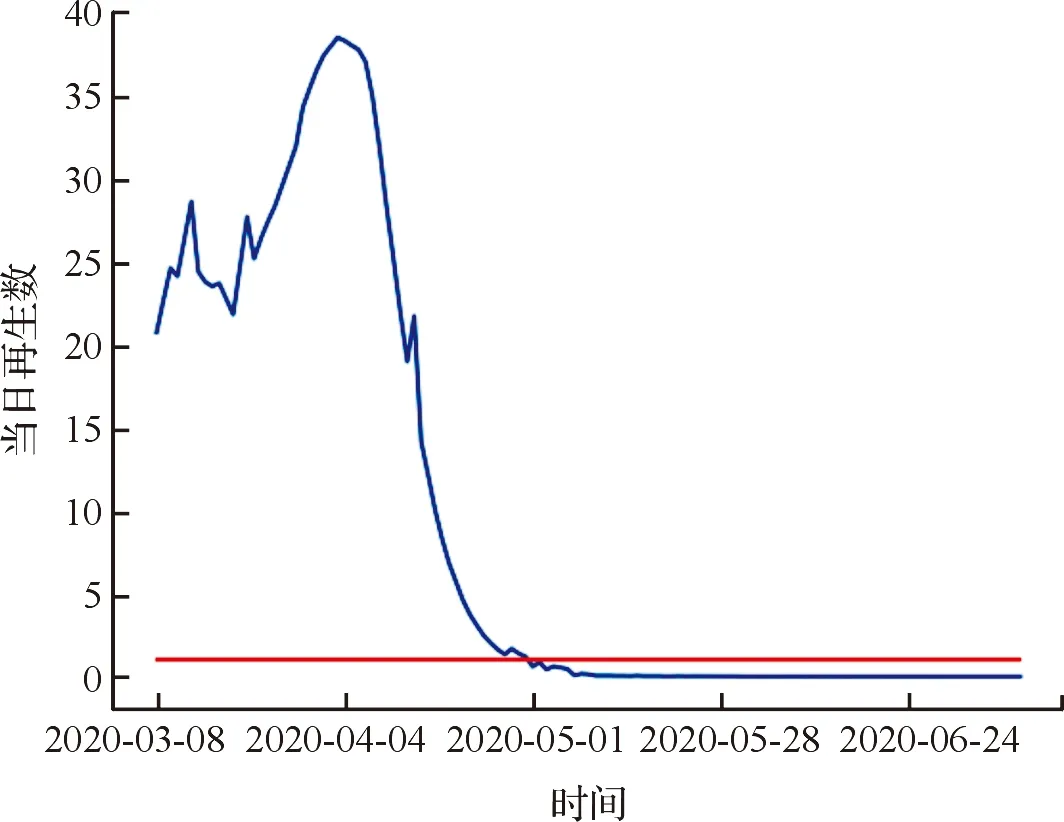
图3 当日再生数随时间的演化情况Fig.3 Change of intraday regenerationnumber over time

从图3中可以发现,在2020年3月8日意大利全国“封城”之后当日基本再生数上下不稳定地波动,总体向上增长。在2020年4月4日时当日再生数达到峰值,之后开始快速下降,隔离措施产生了作用,且当日再生数在2020年5月1日至7月10日一直小于1,疫情得到有效控制。

2.5 隔离措施对疫情传播的影响

从2020年3月8日起,意大利正式签署“封城令”,开始实施欧洲史上规模最大的封城措施。为验证物理隔离对阻断新冠肺炎传播是否有效果。本研究通过提高传染率来模拟意大利不采取封城措施的情形,并与SIR模型预测到的感染者人数放在一起做对比分析,结果如图4所示。

图4 防控隔离措施对疫情的影响Fig.4 Impact of physical isolation measureson epidemic

图4中,I(t)为官方提供的确诊人数;It为模型预测的感染者人数。SIR模型参数β为易感者被感染的平均概率。采取隔离措施相当于降低传染率β,两者高度相关。将模型中的参数β提高到原来的2倍来模拟没有采取“封城”措施时感染者病例数随时间变化的曲线It(2β)。

通过分析我们发现,目前的防控措施对疫情起到了很好的抑制作用。如果不采取相应隔离措施,现存感染人数会比目前高出30 000人左右,也就是说,如果没有封锁措施,将导致感染人数峰值更高且更快达到峰值,造成更大的生命财产损失以及社会恐慌。

2.6 集中收治对感染人数峰值的影响

在新冠肺炎传播的高峰期,医疗人员和物资的供应是一个关键问题。医院的收治效率与SIR模型中的恢复系数γ呈正相关。本研究通过降低恢复系数来模拟医院收治效率不高的情况,结果如图5所示。I(t)为官方提供的确诊病例数;It为模型预测的感染者病例数;It(γ/2)为模型中的恢复系数γ减少到原来一半时的感染者病例数。

图5 医院收治效率对疫情的影响Fig.5 Impact of hospital admission efficiencyon epidemic

从图5中可以看出,集中收治在疫情高峰期可以避免约3万人被感染,在疫情后期现存病例数也明显低于未采取集中收治的状况。综上,集中收治对感染者病例数的迅速回落发挥了关键作用。

2.7 意大利疫情后期的增长趋势

由LSTM模型预测得到的确诊病例数结果如图6～7所示,模型预测的区间为2020年2月11日至8月24日。红色的虚线为模型在训练集上对累计和现存感染人数的预测值,绿色的虚线为模型在测试集上对累计和现存感染人数的预测值,蓝色的实线为截至2020年8月18日官方公布的数据。

图6 LSTM模型累计确诊病例趋势预测Fig.6 Trend prediction of cumulative confirmed cases by LSTM model

从图7中可以看出,在2020年4月21日现存确诊病例数达到峰值后开始迅速下降,隔离措施初见成效。但疫情好转的同时也给意大利经济带来重创,为此意大利在2020年5月4日被迫实行解封措施。从图7可以看出,确诊病例数在达到低点后又开始继续上升且增长速率越来越快,进入二次增长阶段。如果意大利政府在这种情况下放任不管、不采取任何防控措施,势必会导致疫情二次爆发。

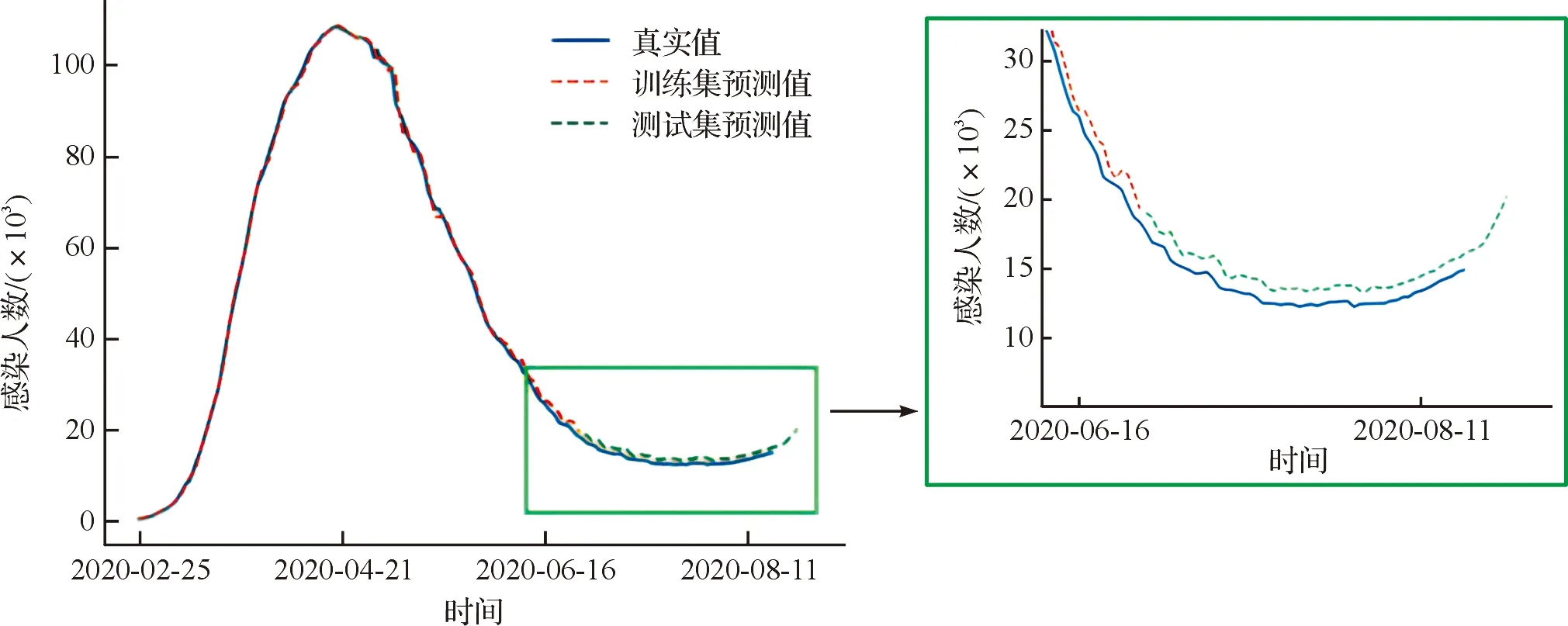
图7 LSTM模型现存确诊病例趋势预测Fig.7 Trend prediction of existing confirmed cases by LSTM model

3 结 论

本研究根据意大利“封城”和“解封”两个重要时间节点,将疫情传播划分为初期(指数上升阶段)、中期(次指数增长阶段)和后期(二次增长阶段)3阶段,并利用logistic回归模型、SIR模型和LSTM模型,对意大利疫情中后期传播过程中感染者的发展趋势进行建模和分析。通过试验验证,拟合结果与实际数据高度吻合,从而可为疫情趋势分析提供有效的数据分析支持。由此得出如下结论:

1) 意大利的缓增期出现于2020年9月29日左右,预计最终累计确诊病例数将达到26.89万人。当日再生数Rt在不断减小,这与政府的防控措施及民众的居家防护有直接关系。

2) 根据模型预测结果,在疫情后期意大利确诊人数会进入二次增长阶段,建议意大利推迟全部企业复工复产及学校开学的时间。目前,意大利疫情控制还不稳定,甚至海外一些国家不仅仅是面对新冠疫情,例如“西尼罗病毒”和“沙门氏菌病毒”席卷美国,新加坡受到“登革热”疫情的困扰。为了防止这些传染病流入中国,我们还需加强出入境管理。