索网结构非线性有限元分析中初始张力状态的快速构造方法

王 威，吴 松，郭其威，唐国安

（1.复旦大学 航空航天系，上海 200433；2.上海空间飞行器机构重点实验室，上海 201108；3.上海宇航系统工程研究所，上海 201108）

0 引言

索网结构是张力结构体系的一个重要组成部分，其具有重量轻、强度高、收缩比大、成形多样等显著优点［1-2］，可被应用于太空可展开天线领域。预张力是索网结构成型的必要条件和提高其曲面稳定性的重要参数［3-4］。

在结构负荷工作阶段，无论其静力行为还是动力行为均体现出较高的非线性特性［5-6］，然而由于航天发展所需天线趋于大型化，结构全尺寸地面试验难以开展［7］，所以在设计阶段，有限元数值分析显示出了巨大优势。

有限元分析时，预张力的施加方法有等效荷载法、降温法、初始应变法等［8-17］。而对于复杂的索网结构，等效载荷法并不适用，初应变法与降温法本质相同，都是通过改变索网的单元原长度来施加预张力。根据是否进行迭代，确定初应变（或降温量）的方法可分为迭代修正法和直接法。迭代修正法先取一个初应变（或降温量）计算索单元的预张力，根据结果与设计值的差异修正初应变（或降温量），然后再重新计算，直至迭代收敛［9-10，13］。在现阶 段，这是一 种常用 的计算方法，但需要迭代计算，会导致效率降低。直接法不需要迭代，效率高。张航［11］和YANG 等［18］提出了考虑支座位移的计算方法，将总降温值分为拉索两端固定时达到设计预张力所需的降温值，支撑结构位移带来的拉索变形所对应的降温值两部分叠加。此种方法没有考虑两部分降温值之间的耦合效应，应用于复杂的非线性结构时精度并不高。因此，需要一种能在利用有限元数值方法分析时，满足高精度和高效率的初应变（或降温量）的计算方法。

针对上述问题，本文综合考虑索网的几何非线性、刚度矩阵奇异性、框架的变形、预张力施加精度和计算效率等因素，提出了一种新的确定索网初应变（或降温量）的方法。该方法以无预应力索网结构的有限元模型为基础，迭加上带预紧力柔索的初应力刚度矩阵，使得能够借助通用程序MSC/NASTRAN 直接计算出降温量，用于模拟索网的预张力。此方法综合了迭代修正法和直接法的优势，计算过程简便，可操作性强，能保证计算精度，有效提高了效率。对应用于卫星可展开天线在内的复杂、多层、具有弹性约束的索网结构，没有构型限制，且可进一步开展非线性固有频率和响应的计算。

1 索单元预紧力降温模拟的线性化计算方法

1.1 几何非线性问题的单元切线刚度矩阵

由虚功原理可知，在平衡力系作用下的单元内，应力σ(e)在虚应变δε(e)上作的功等于等效节点力F(e)在虚位移δq(e)上作的功，即

根据连续介质力学的几何方程，虚应变又可以用虚位移表示：

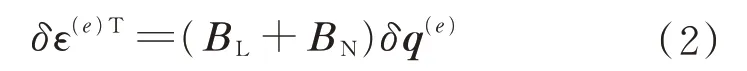
式中：BL为与变形无关的线性应变矩阵；BN为与位移q(e)有关的非线性应变矩阵。

将式（2）代入式（1）中，根据虚位移δq(e)的任意性，可以得到单元的平衡方程：

式中：Ω为体积域。

在材料屈服极限内，应力-应变关系依旧可以用胡克定律表示：

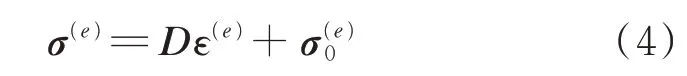
式中：D为材料的弹性矩阵；为单元的初应力向量；ε(e)为单元的应变向量。

将式（4）代入式（3）中，可得

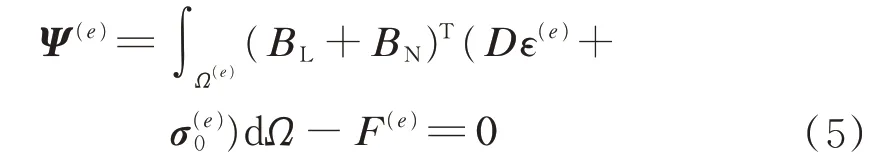
因为矩阵BN和向量ε(e)均与q(e)有关，所以Ψ(e)是q(e)的非线性函数，式（5）是关于与q(e)的非线性方程组。非线性方程组一般采用迭代法求解，例如，具有二次收敛速度的牛顿-拉夫逊（Newton-Raphson，N-R）算法。N-R 算法需要提供函数Ψ(e)关于自变量q(e)的梯度

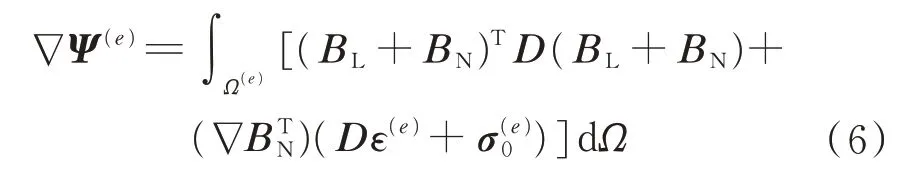
推导过程利用了关系∇ε=BL+BN，这里符号∇为梯度算子。若记

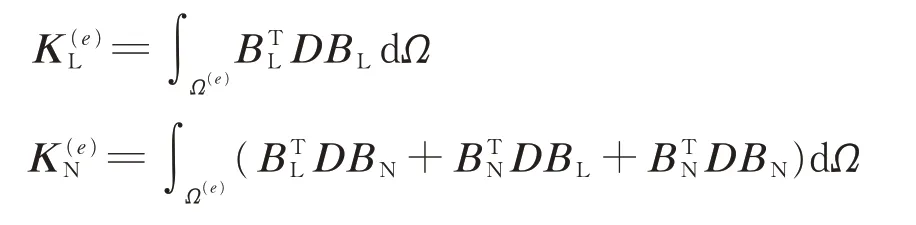
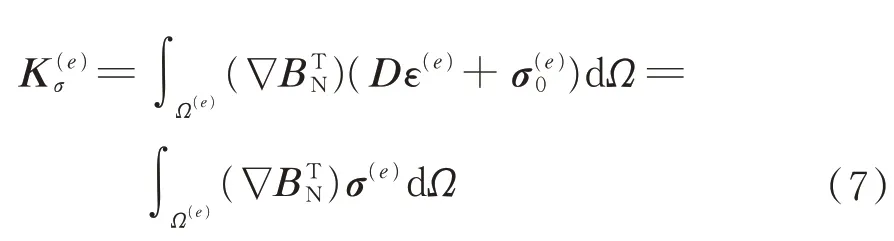
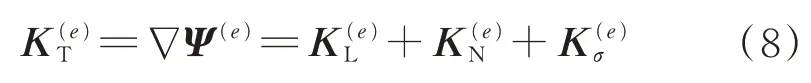
1.2 预张力索单元的初应力刚度矩阵

关于位移分量求变分后得到

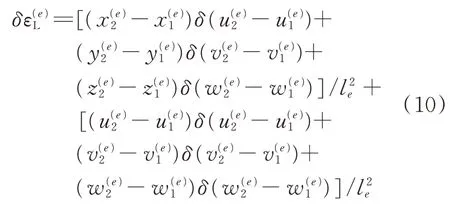
对比式（10）与式（2）可知，索单元的线性和非线性应变矩阵为

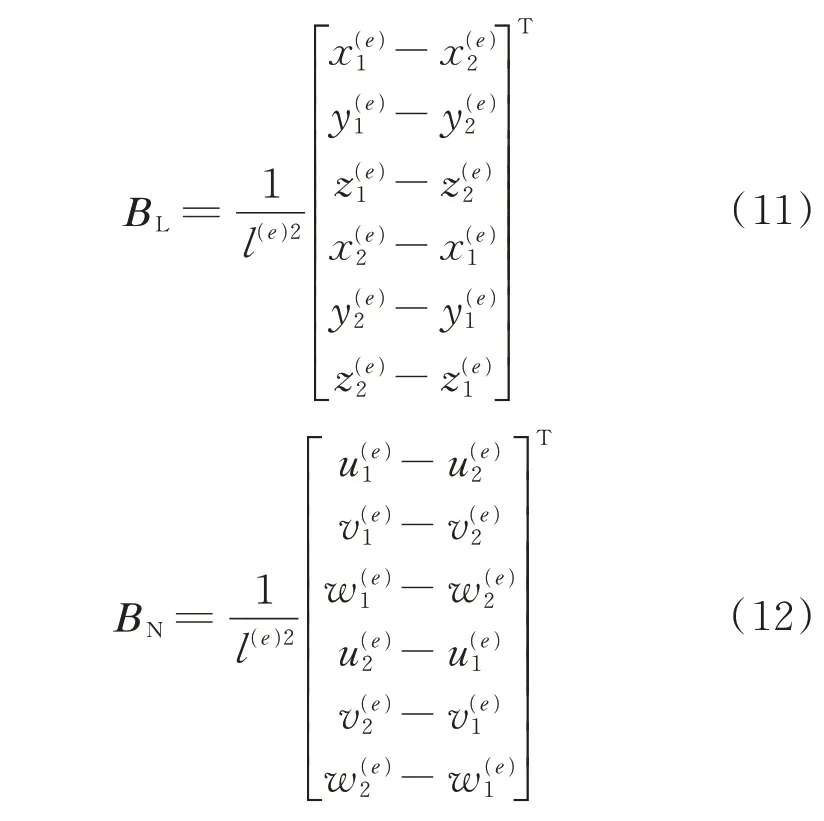
再对式（12）的BN求变分，还能得到

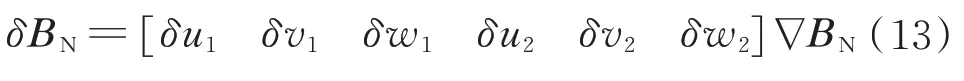
式中：

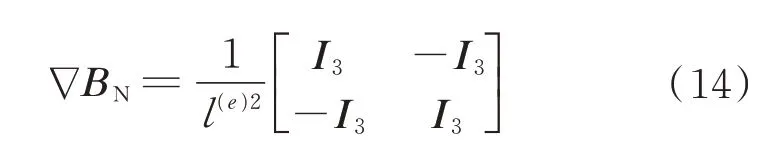
式中：I3为3×3 的单位阵。

若给定索单元的预张力Ne，根据式（7）、式（8）以及式（11）、式（12）和式（14）便可计算出预张力索单元的初应力刚度矩阵

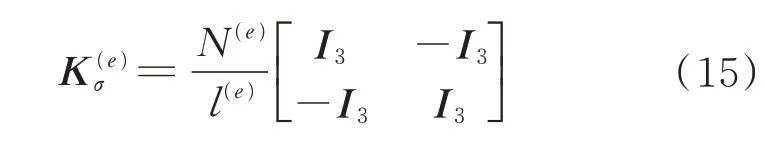
1.3 降温值计算

对于由柔索和弹性构件组成的索网结构，用“节点-单元-材料-属性”等常规的数据定义初始有限元模型。从模型数据中筛选出柔索单元，根据柔索张力的设计要求，按照式（15）逐个计算单元的初应力刚度矩阵Kσ(e)，再用常规的有限元装配过程组装成整个索网的初应力刚度矩阵Kσ。

将初应力刚度矩阵Kσ迭加到索网结构有限元模型的线性刚度矩阵上，近似地等效出索网结构带有张紧力时的切线刚度矩阵。这样处理后索网结构的刚度矩阵不再具有奇异性，而且是与变形或位移无关的常矩阵，可用线性方法进行计算。采用通用的有限元程序计算时，可以用降温产生的收缩力等效柔索的预紧力。假设柔索单元的序号是1～nc，依次在柔索单元j上施加单位负温度，计算出每一个柔索单元的张力，记为cij(i=1，2，…，nc)。当编号j从1 到nc遍历全部柔索单元后，就得到了以cij为元素、温度对张力的影响矩阵C，这时C是一个nc×nc非奇异阶矩阵。如果柔索单元张力的设计值是N(i)(i=1，2，…，nc)，那么各个柔索单元上需要施加的负温度T(i)(i=1，2，…，nc)应满足关系

式中：N、T分别为由N(i)和T(i)排成的列向量。

上述方法在计算柔索单元的张力cij时，虽然略去了大变形刚度矩阵，但保留了切线刚度矩阵中占主导的初应力刚度矩阵和线性刚度矩阵，因此具有较高的计算精度。且在张力已知的情况下，初应力刚度矩阵是常矩阵，计算C矩阵的每一列可作为相同模型、不同工况问题求解，不需要重新生成和分解切线刚度矩阵，所以方法又具有较高的效率。

2 实施过程和简例验证

2.1 验证模型的定义

用于说明算法的索网与结构组合体有限元模型的示意图如图1 所示。图中，带有#的数字为节点序号，小括号内的数字为单元序号。单元（1）～单元（5）是组成索网的五根柔索，材料为尼龙绳（弹性模量取1.5 GPA），其中，长 度l1=0.2 m 的横索网（1）～横索网（4）和长度l2=0.1 m 的竖索网（5）分别用截面抗拉刚度EA1=3 000 N 和EA2=150 N 的杆单元建模，支撑构件（6）和支撑构件（7）用刚度系数为k=105N/m 的接地弹簧建模。设计要求横索网和竖索网的张力分别是N1=100 N，N2=1 N。考虑在平面内的变形，该索网结构组的 自由度为 6，对应的 位移分量u2、u3、u5、u6、v2、v5已标注图1 中。

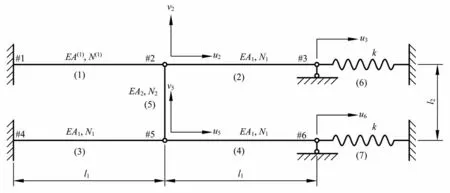
图1 简单模型的结构示意Fig.1 Structural sketch of simple model

算例用有限元分析程序NASTRAN 计算，模型的定义见表1。定义模型的数据包括节点坐标、单元组合信息、材料常数、单元属性和约束条件。为了便于分析，将柔索材料的热膨胀系数设置为α=1。采用这样的设置，施加在柔索单元上温度载荷T(e)就是单元单位长度的伸长量。由图1可见，模型中节点2 和节点3 在纵向没有刚度，索网与结构组合体的整体刚度矩阵是奇异的。为克服奇异性，在表1 中补充了第20 行Include‘KSIGMA.pch’，其内容是将要迭加的初应力刚度矩阵Kσ。

2.2 初应力刚度矩阵的生成

根据表1 中单元（1）～单元（5）的组合信息和相应的节点坐标，用算法语言自行编制程序，算得这5个单元构成的索网初应力刚度矩阵为

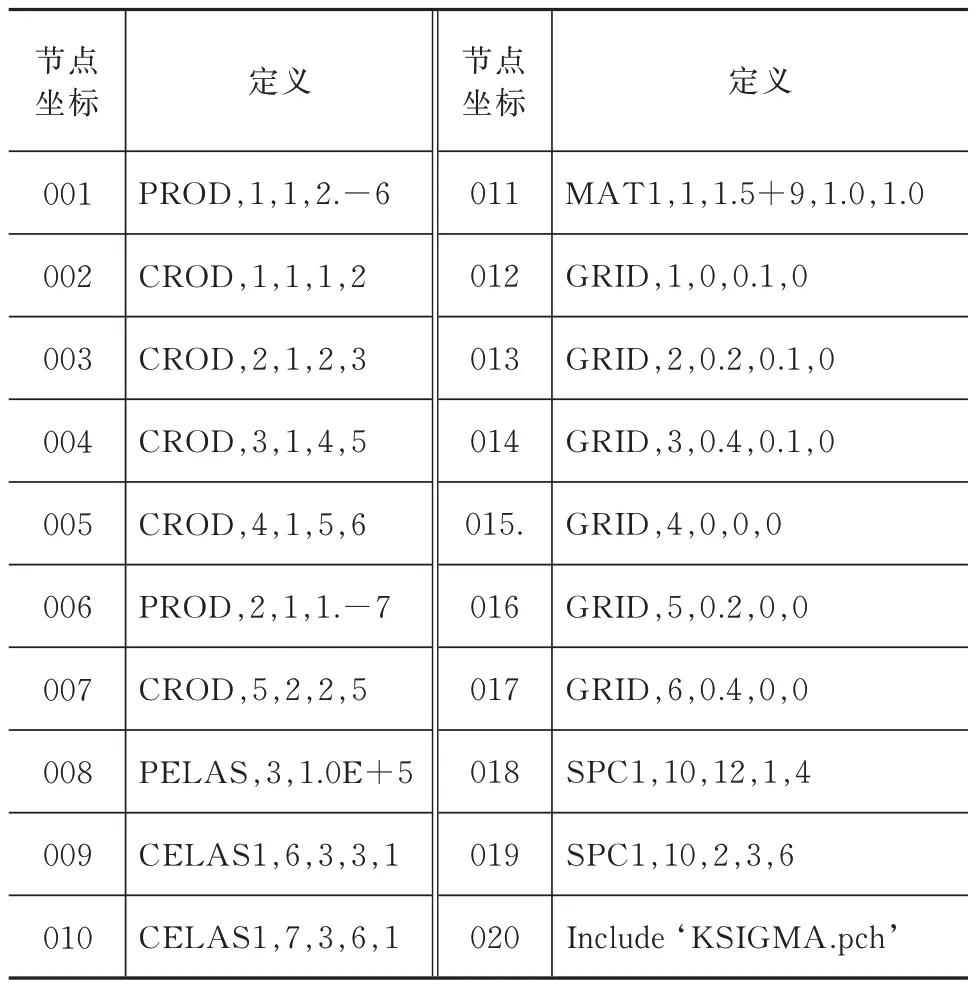
表1 索网结构算例的有限元模型定义Tab.1 Definitions of the finite element model for cable net structure

式中：Kσ的单位为N/m。

该矩阵是对称的，其6 行（或者6 列）对应的位移分量在模型中分别是u2、v2、u3、u5、v5和u6。参照NASTRAN 的DMIG 格式要求，将Kσ命名为KSIGMA，下三角部分元素按行顺序写到外部文件，取名为KSIGMA.pch，见表2。

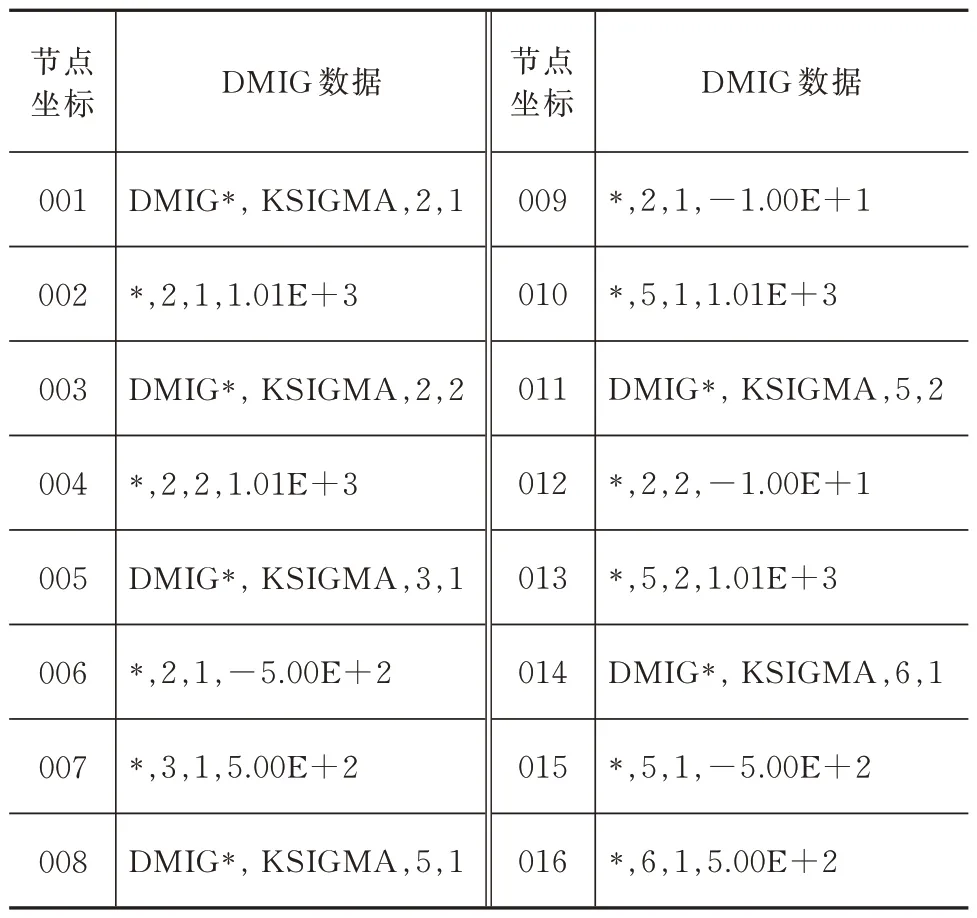
表2 初应力刚度矩阵的DMIG 数据Tab.2 DMIG data of the initial stress stiffness matrix

2.3 温度对张力的影响矩阵生成

为了得到温度对张力的影响矩阵C，再建立一个NASTRAN 的输入文件，见表3。

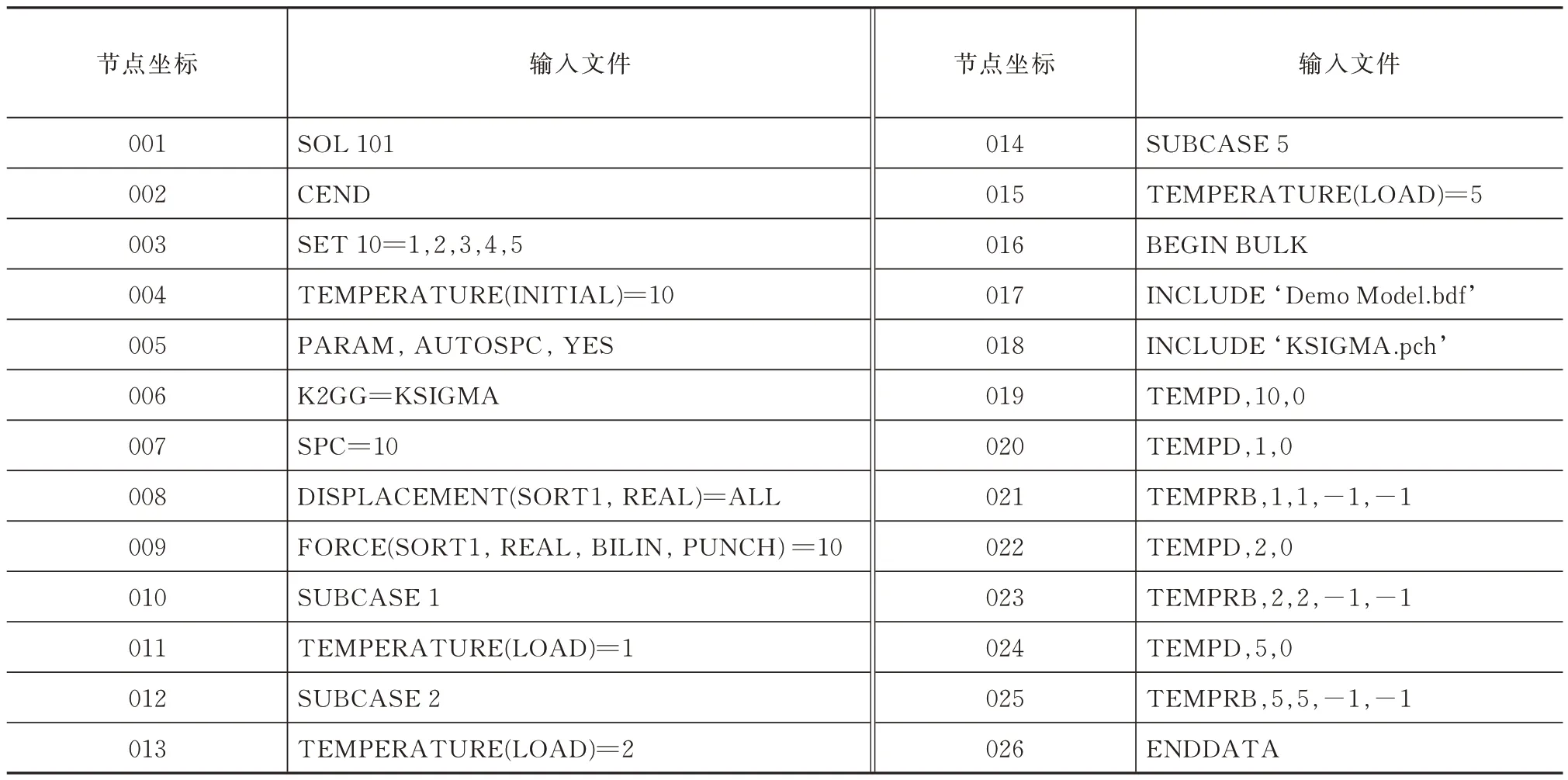
表3 计算温度对张力影响矩阵的NASTRAN 输入文件Tab.3 NASTRAN input file for calculating the effect matrix of temperature on tension

该输入文件包含3 个计算工况，分别对应于在柔索单元（1）、单元（2）和单元（5）上施加单位负温度，求解5 个柔索单元的张力。由于影响矩阵以及结构均具有对称性，单元（3）和单元（4）上施加单位负温度的工况可以用工况1 和工况2 替代。运行NASTRAN 后，经整理得到

式中：矩阵中只有变量名、没有具体数字的元素为可以利用结构或矩阵对称性替代的数据。

2.4 耦合变形和张力的计算分析

根据五根柔索张力的设计值100、100、100、100和1 N，用式（17）给出的矩阵C根据式（16）可算得每个单元的温度为

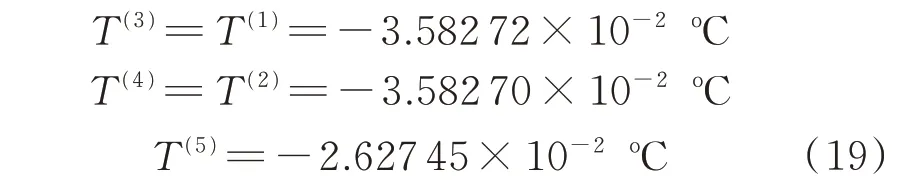
将这组温度值作为已知单元温度载荷条件，建立的NASTRAN 输入文件，见表4。

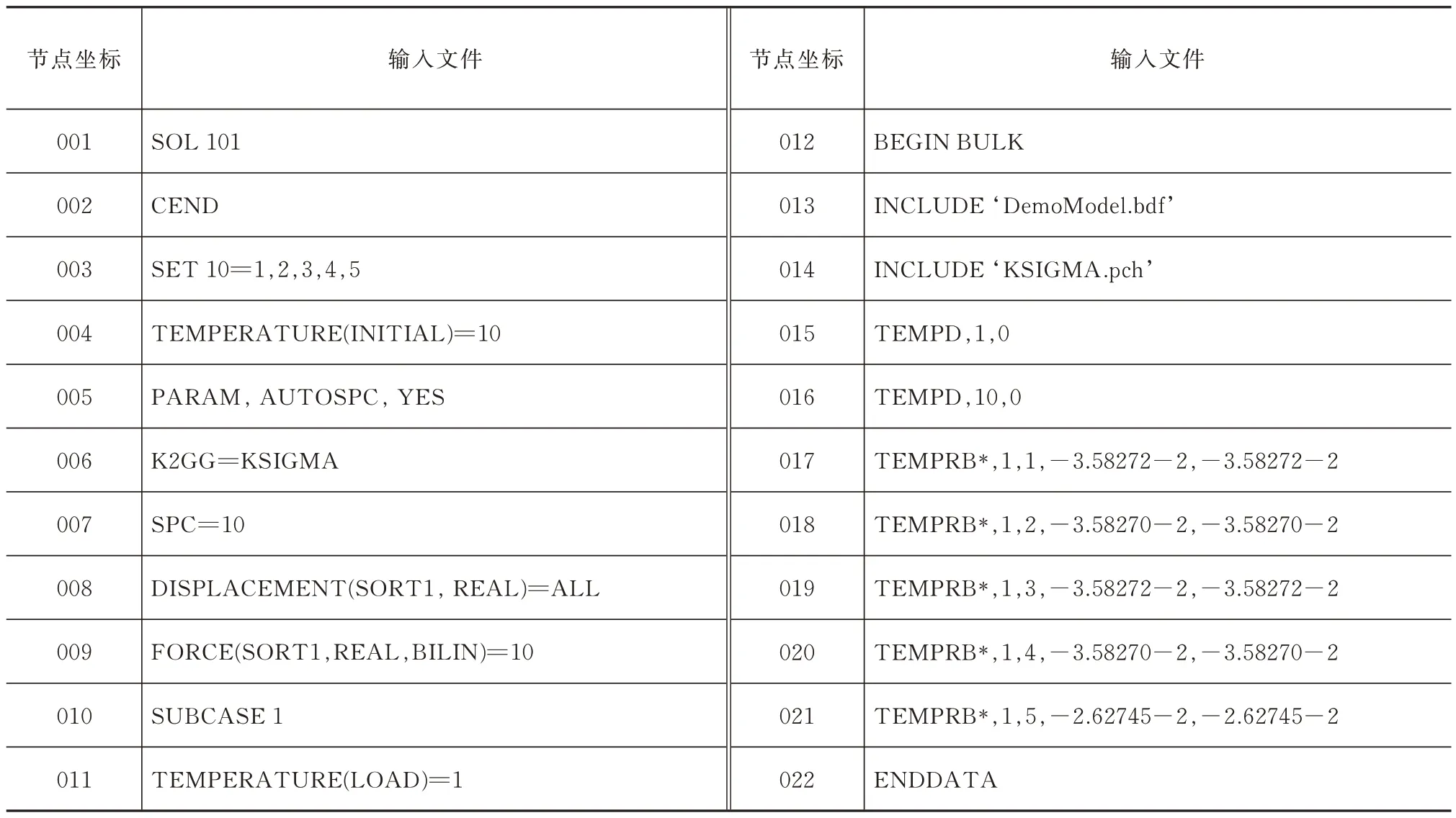
表4 耦合变形和张力计算的NASTRAN 输入文件Tab.4 NASTRAN input file for coupled deformation and tension calculation

计算后得到的柔索单元张力与设计值完全一致。关于变形的位移分量可以在微小位移假设下用解析法估算。参考图1，节点3 的横向位移就是在柔索（1）和柔索（2）张力N1作用下支撑弹簧（6）的伸长量，即柔索（1）和柔索（2）的收缩量相同，其和等于u3，因此-5×10-4m。节点2 竖向位移使得柔索（1）和柔索（2）的张力N1改变方向，其竖向的分量和与柔索（5）的张力N2平衡，由此得出-10-3m。位移分量的有限元计算与解析法估算结果的对比见表5，两者相差无几，表明用本文介绍的方法具有很高的计算精度。

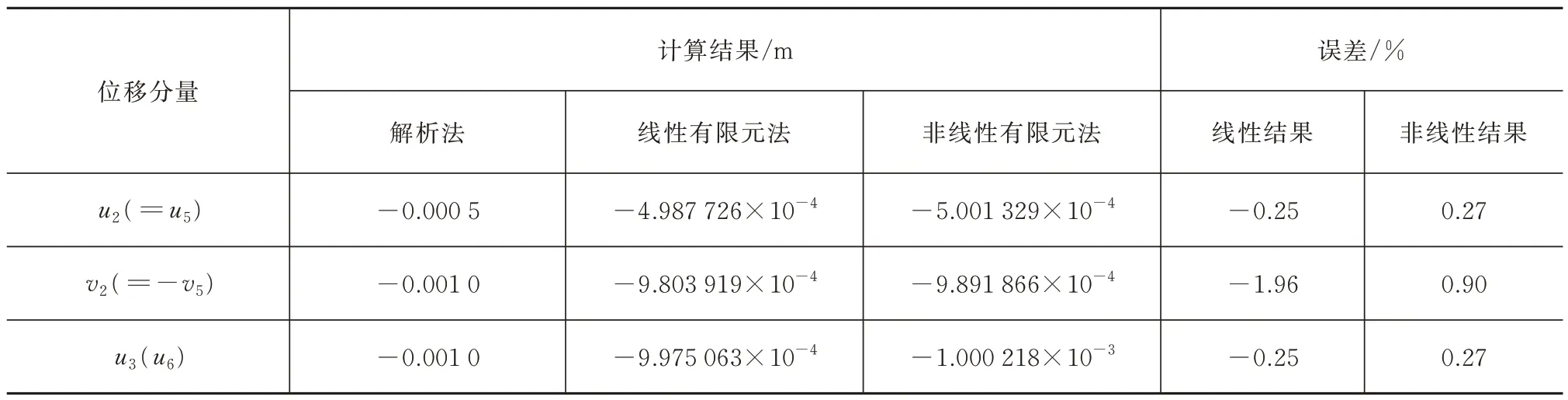
表5 预紧力索网-结构算例耦合变形的计算结果Tab.5 Calculation results of the coupled deformation of the cable net structure with pretension

配置柔索等效温度下降量、后续的耦合变形和张力计算都是线性过程，不需要迭代就能取得很高的计算效率。当预紧力的等效温度确定后，作为已知载荷问题也可以用非线性分析计算索网-结构的耦合变形。此时，将横索网和竖索网分别等效为边的方型截面梁单元，利用细长梁较弱的横向刚度避免零张力状态下索网刚度矩阵的奇异性，实现非线性计算的初始迭代。用NASTRAN 求解序列106 计算，得到的横索网张力均是100 N，与设计值完全吻合，竖索网张力是0.974 4 N，误差约为-2.56%，符合工程计算的精度要求。位移的非线性计算结果见表5。解析法与线性和非线性方法得到的结果误差相当。

3 索网式天线动力学特性计算的工程应用

索网式反射面天线如图2 所示，结构包括伸展臂、支撑桁架、索网3 个主要部分。支撑桁架是由辅助驱动单元、外生支撑单元、立柱或助杆接头组成，索网包含前索网、背索网、张紧索和斜拉索。天线支撑桁架左右跨度为14.76 m，前后跨度为12.00 m。

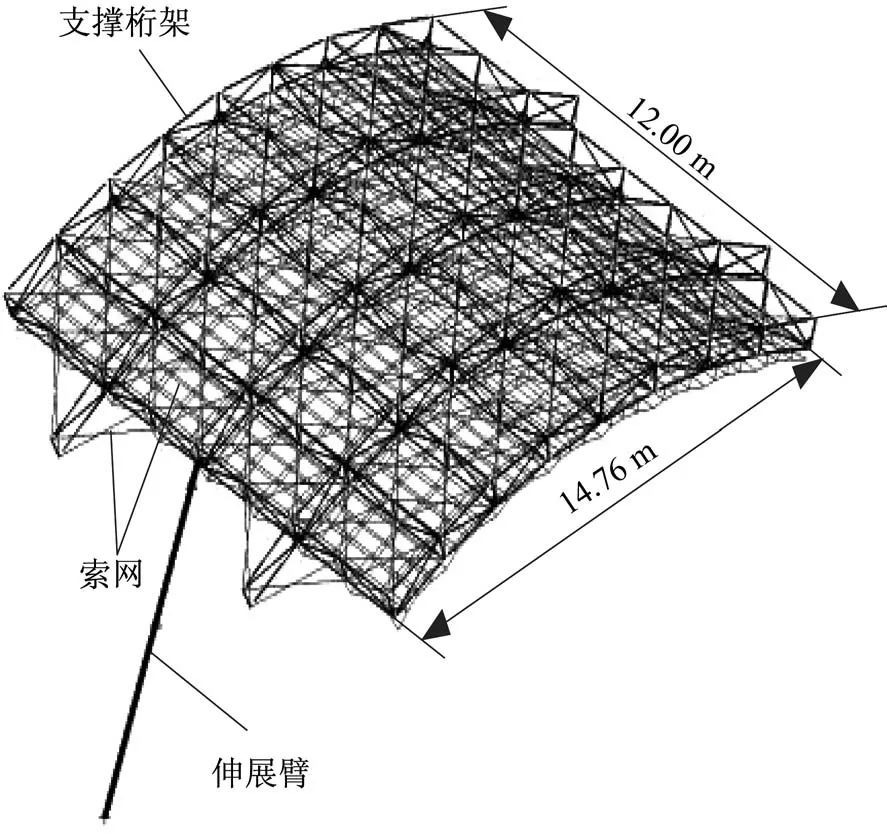
图2 索网式可展开天线Fig.2 Cable net deployable antenna

运用上述算法，根据索网预张力设计值，配置索网单元的等效温度下降量并作为输入条件，然后采用SOL 106 求解序列，进行非线性静力分析。分析时，设定伸展臂根部固支，索网预张力施加结果如图3 所示，与设计值相比，相对误差处于2.3%以下，因此能满足设计阶段的精度要求。在预张力作用下的索网、支撑桁架和伸展臂耦合变形的计算结果如图4 所示。图中，粗实线为变形放大50 倍后的状态，节点位移的最大值在厘米量级。结合预张力施加精度及变形结果可知，以线性刚度矩阵和初应力刚度矩阵的叠加等效带有张紧力的索网结构的切线刚度矩阵，在实际工程应用中是可行的。

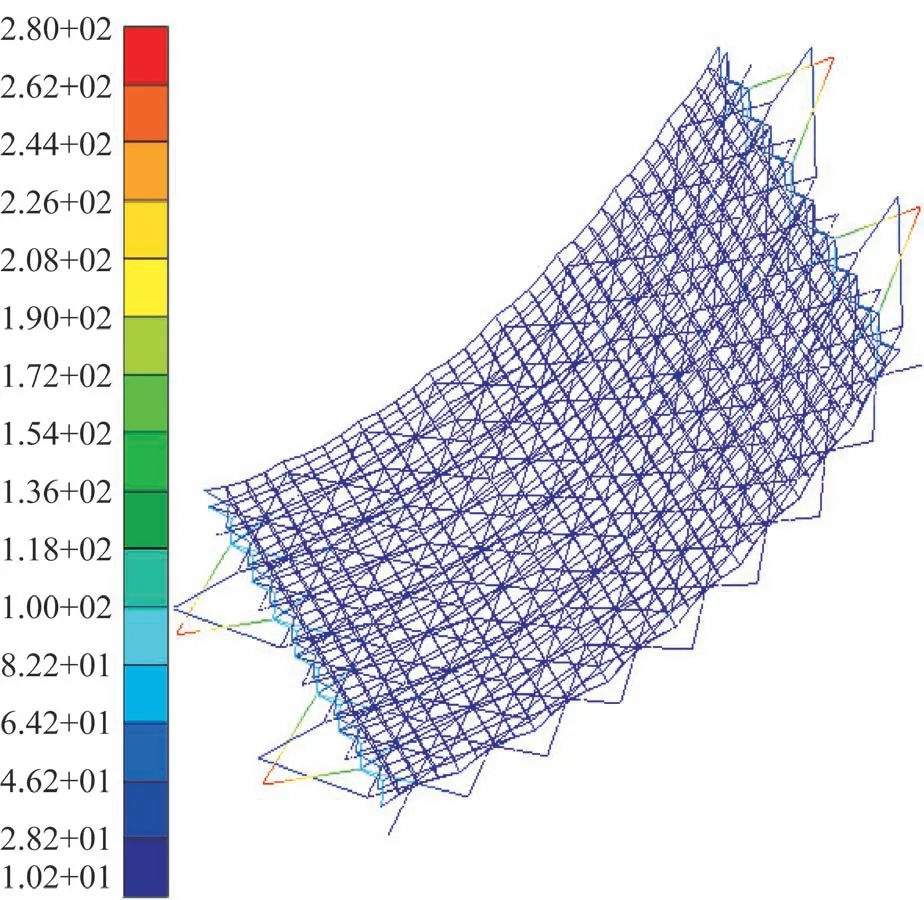
图3 索网预张力施加结果Fig.3 Result of pretension application to cable net

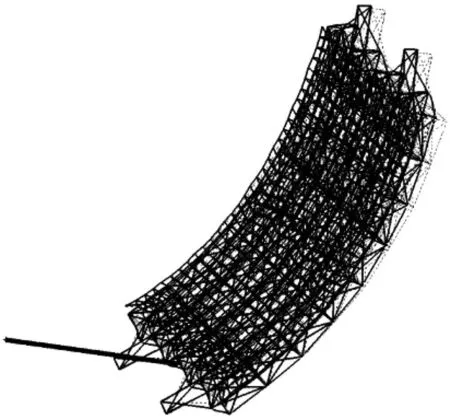
图4 索网、框架和伸展臂的耦合变形Fig.4 Coupling deformation of cable net，frame，and extension arm

同样采用SOL 106 求解序列，根据存在预张力状态时的切线刚度矩阵进行模态分析，天线的前6阶固有频率以及与其对应的振型如图5 所示。图中：第1 阶和第2 阶主要为伸展臂的弯曲模态，由伸展臂自身刚度决定；第3 阶为天线整体的1 阶扭转模态；第4 阶主要为支撑桁架与索网结构的1 阶扭转模态；第5 阶主要为伸展臂的局部模态，受到伸展臂自身连接刚度影响；第6 阶为天线整体的2 阶扭转模态。

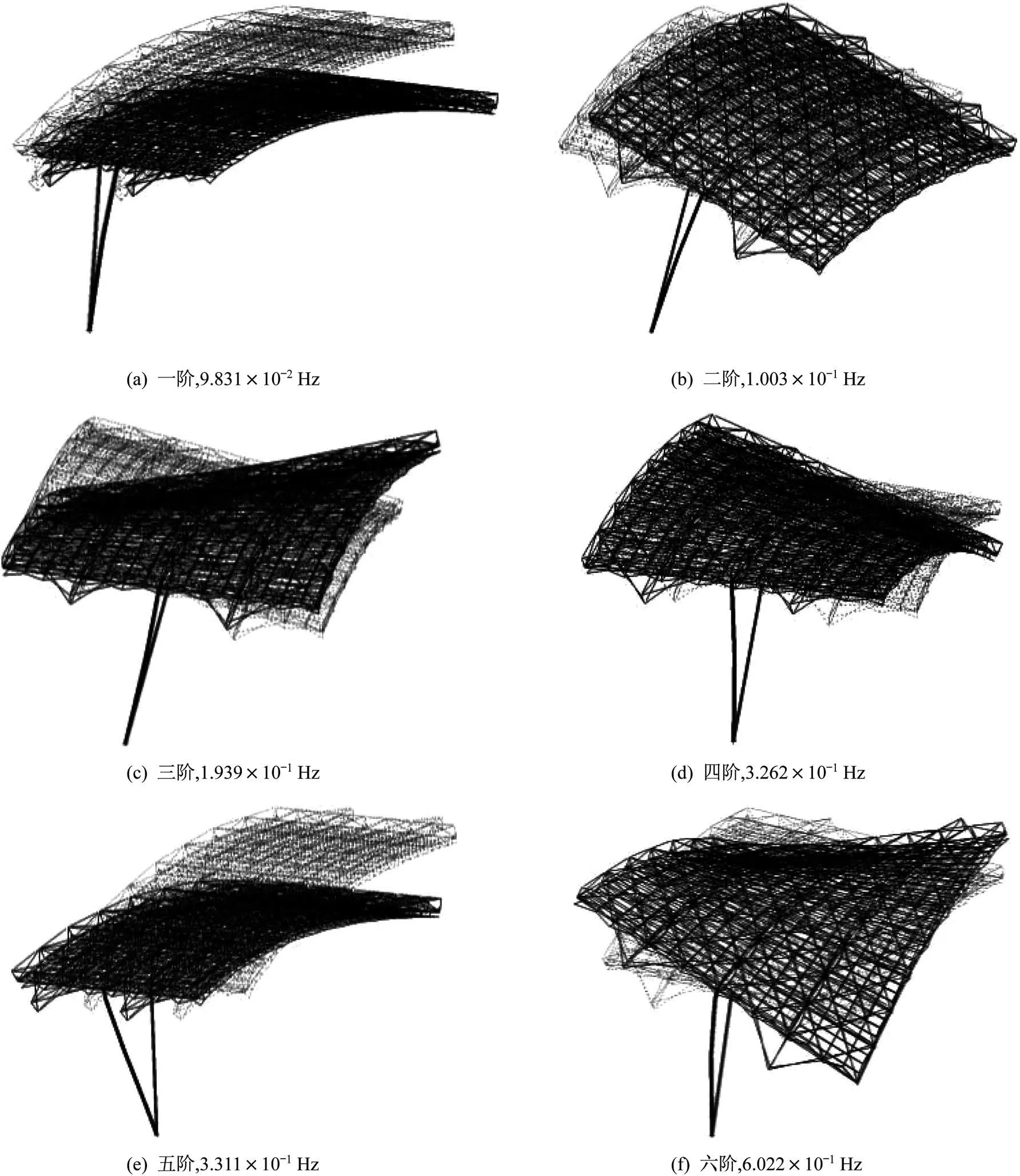
图5 非线性固有模态Fig.5 Nonlinear natural mode

4 结束语

本文针对简单柔索算例的详细分析，以及在实际索网结构工程中的应用，表明对于几何非线性效应显著、横向刚度中张紧力占主导的索网单元，在单元切线刚度矩阵中略去因位形改变而引起的初位移刚度矩阵，而保留由张力所产生的初应力刚度矩阵，能够有效计算出用柔性索单元的预紧力。由于保留的初应力刚度矩阵是常量，因此，预紧力的计算属于线性问题，具有很高的计算效率。将所得的预紧力用降低温度的方法比拟，用热弹性有限元计算出的柔索张力能够与设计值高度吻合。对于航天器上应用的索网天线，本方法能在保证精度的前提下提高计算效率。此外，整个过程可以充分利用通用有限元计算程序，可以在此基础上进一步开展模态和响应等力学计算，便于在工程中应用和实施。