黎曼流形上光滑函数的Hessian在共形度量下的关系式

田大平，汪敏

(江汉大学人工智能学院， 湖北 武汉 430056)

0 引言

黎曼流形上光滑函数的Hessian，就是对光滑函数的1次外微分式(约定为1次微分式，即光滑的一阶协变张量场)求协变微分而得到的一个对称的二阶协变张量场. 由此， 可以定义黎曼流形上的Hessian算子[1-2]. 对于Hessian算子的研究已有许多不同的结论. 如Birtea-Comănescu[3]研究了约束流形上的Hessian算子，Hung-Quy[4]研究了Deltam-次调和函数的一些加权能量类上的m-Hessian算子，Wan-Wang[5]研究了无界m次调和函数的复Hessian算子和Lelong数. 另外，对于涉及Hessian算子的其他问题的研究也有很多结论. 如Covei[6]研究了k-Hessian算子的 Keller-Osserman问题，Xiao-Zhang[7]研究了Hessian算子的等容量估计，Ye[8]讨论了球中Hessian算子本征函数的对数凸性，Nina-Ivochkina-Nadezhda[9]研究了关于m-Hessian算子理论中的两个对称问题, Ferrari-Medina-Peral[10]讨论了涉及第2个Hessian算子的双调和椭圆问题.

本文中，我们将根据黎曼流形上Hessian算子和黎曼共形度量的定义，来考虑光滑函数的Hessian的分量在黎曼共形度量下的关系式.

1 预备知识

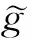
定义1.1[1]光滑的一阶协变张量场(即余切向量场)称为1次微分式.

光滑流形M上的全体1次微分式的集合记为A1(M),即

定义1.2[1]光滑流形M上的一个光滑的r阶反对称协变张量场称为M上的一个r次外微分式.

特别约定:M上1次外微分式就是M上的1次微分式，即光滑的一阶协变张量场；M上0次外微分式就是M上的光滑函数.

M上的r次外微分式的集合记作Ar(M).特别地,

若记

则在A(M)上可以定义外微分运算.

定义1.3[1]设M是m维光滑流形，则存在唯一的一个映射

d:A(M)→A(M),

使得对于任意的非负整数r，有d(Ar(M))⊂Ar+1(M), 并且满足以下条件:

1)d是线性的, 即对任意的φ,ψ∈A(M),μ∈R，有

d(φ+μψ)=dφ+μdψ;

2)∀φ∈Ar(M),ψ∈A(M),有

d(φ∧ψ)=dφ∧ψ+(-1)rφ∧dψ;

3)∀f∈A0(M),df是f的微分；

4) d2=d∘d=0.

称这样的映射d为外微分(算子).

定义1.4[1]设(M,g)是m维黎曼流形，X∈(M), (U;xi)是M的局部坐标系, 并且若存在映射使得

是与局部坐标系的选取无关的(1,1)型光滑张量场, 则称映射D为黎曼流形(M,g)上的协变微分算子.

上式中的函数

(1)

由度量的分量gij完全确定, 叫做黎曼度量g在局部坐标系(U;xi)下的Christoffel记号.

对于任意f∈C∞(M), 则

对df求协变微分得到一个二阶协变张量场，记为Hess(f),即

Hess(f)称为光滑函数f的Hessian.

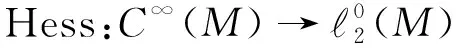
在M的局部坐标系(U;xi)下，有

(2)

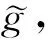
2 主要定理及证明

这一节, 我们将给出本文中的主要定理, 并且完成定理的证明. 为此, 首先给出下面的引理. 这个引理的结论在文献[1]的习题中已经给出，但是没有证明过程. 为了本研究完整性，我们首先证明这个引理.

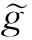
特别地, 若λ=eρ,ρ∈C∞(M), 则上式成为

引理2.1的证明由(1)式可知

(3)

取λ=eρ,ρ∈C∞(M)代入(3)式，可得

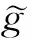
特别地, 若λ=eρ,ρ∈C∞(M), 则上式成为

定理2.2的证明在M的局部坐标系(U;xi)下，由(2)式及引理2.1可得

取λ=eρ,ρ∈C∞(M)代入上式，可得

定理得证.