借助直观演示，促进有效教学

林强

摘要：直观教学是小学数学教学中非常重要的一种手段，它的特点就是能够结合学生的实际，从学生的角度出发，结合教育内容，运用多种形式为学生提供感性认识材料，使学生在感性直观与操作体验中实现从具象到抽象的认知理解过程，从而加深对数学概念、法则及数量关系的认识。

关键词：直观演示;学具操作;图形直观

小学生学习数学，由于受经验不足、所接触的思维方法有限、语言表达能力不强等因素的影响，导致学习效率低下。因此，在数学教学中，教师应借助直观演示、学具操作等，帮助学生理解所学知识，提高课堂教学的有效性。

一、借助直观演示，理解概念本质

概念教学类的课型，大多枯燥乏味，但这类课题尤其需要老师帮助学生建立一个直观的模型，利用模型直观帮助学生掌握概念中的重点与关键。例如，在教学“长度单位（厘米）认识”一节课时，怎么让学生认识1厘米呢？首先从尺子上找出1厘米，这是学生对1厘米初步的直观认识，若仅限于此，学生在头脑中对1厘米的印象肯定不够深刻。而且我们还要引导学生先用拇指和食指照着尺子上的1厘米进行比划，然后把尺子拿掉，看看1厘米到底有多长，再让学生画出1厘米长的线段。然后让学生找一找，身边哪些物体的长度大约是1厘米。学生通过观察，可以发现我们食指的宽度大约是1厘米。这些丰富的表象无形中就在学生的脑海里形成了直观模型，把抽象概念转化成直观模型，由感性认知升华到理性认识。同时，在估计线段长度时，也可以利用食指的宽度进行对照，在实际运用过程中，既巩固了1厘米的长度概念，又渗透了建模思想。这样，在今后学习其他单位时，可以根据之前的学习经验，通过模型直观来内化抽象概念。

二、借助学具操作，弄清计算算理

在计算教学中，我们往往会发现，学生对于计算方法有时会出现混淆，导致计算错误。究其原因，是因为他们不理解算理，对于计算方法只停留于机械性记忆的层面。如何帮助学生理解算理既是计算教学的重点，也是一大难点。通常我们可以借助小棒等有效学具，让学生动手操作，教师要适时进行点拨，让学生在操作的过程中弄清算理。

例如，在教学“100以内进位加法” 一节课时，即计算35+37=，学生利用先前不进位加法的学习经验，发现此时个位相加满10，那么应该怎么办呢？此时老师不要急于教授方法，可以让学生利用小棒摆一摆，摆的时候满10根捆成一捆。师：现在零散的小棒有几根？又有几捆小棒呢？有了直观的动手操作后，在老师的追问下，学生将感性活动认知慢慢转化为理性的认知，从而突破了难点。

同样，在教学“100以内退位减法”一节课时，即例题53-7=，发现个位上3减7不够减，怎么办？此时，学生调动之前的学习经验，利用小棒摆一摆。在摆的过程中，学生会出于本能把一捆小棒拆开。师：一捆小棒拆开后是几根？（10根）现在零散的小棒共有几根？（13根）还有几捆小棒呢？（4捆）师：那么，“13-7”应该怎么拿呢？让学生通过动手操作，再加上教师的适时追问，让他们在操作中悟出“个位不够减，从十位退1当作10”这个算理。那么接下来的计算过程及计算方法的小结就水到渠成了。因此，动手操作能够充分调动学生的思维能力，让他们在操作的过程中理解算理、掌握算法。

三、借助图形直观，分析数量关系

低年级的学生普遍存在抽象思维能力较弱、理解能力较差的现象，这就导致了许多孩子对解决问题望而生畏。那么如何培养学生分析解决问题的能力呢？笔者认为利用图形来表示题意是学生比较能够接受且能够掌握的一种方法。

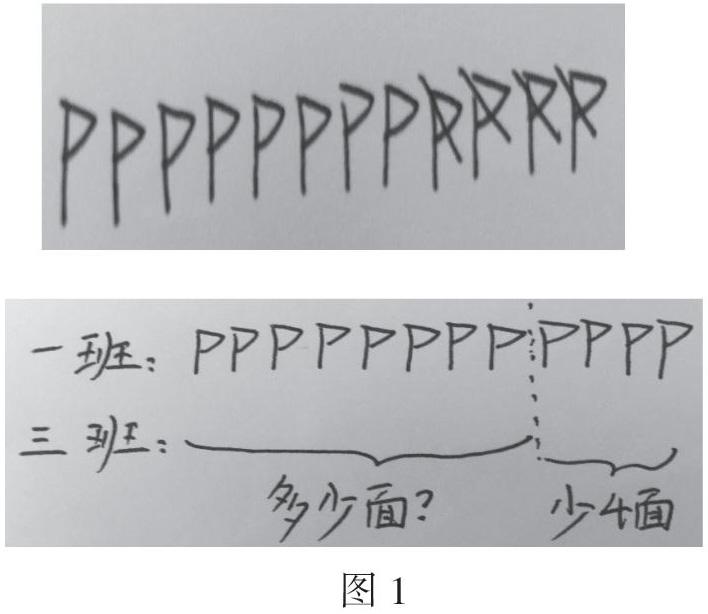
例如，人教版二年级数学中有这样一道题：二年级一班得了12面小红旗，三班的小红旗比一班少4面，三班得了多少面？教学时，先让学生把已知信息用示意图画出来。这样，看似简单的步骤实际上能够使学生自主地去发现题目中的已知信息，找出比较的对象，明确要求的问题。在画的过程中，不同的学生有不同的表示方式，如图1所示：

这正是学生思维方式的不同体现。这时，教师不要急着去规范学生所画出来的图，而要以此为契机，了解不同层次学生的不同思维方式，从而让不同层次的学生在数学上有不同层次的发展。画图能够把题目中的数量关系以直观图形的形式呈现，不仅渗透了数形结合的思想，还蕴含着转化的思想。当学生能利用图形正确表达题意后，就把这道解决问题转化成一年级学过的看图写算式的题型。

又如，教学“植树问题”一节课时，我们很多老师都重视“植树问题”的三种不同类型的分类：两端都种（+1），只种一端（不加不减），两端都不种（-1）。但在教学中，我们不应停留在“结果”上，而应关注“过程”。“植树问题”的本质是渗透了“一一对应”的数学思想，只要弄清了“点”与“树”之间的对应关系，突出“一一对应”的数学思想，学生就能灵活地运用知识去解决相关的“植树问题”。那“一一对应”的数学思想是怎么进行渗透呢？“画线段图”就是其重要的教学策略。比如，同学们在全长20米的小路上一边植树，每隔5米栽1棵，要栽几棵树？让学生独立思考，动手画一画，看看究竟能栽几棵。然后指名汇报，出现以下三种情况（如图2所示）。

学生经历画图过程，利用形象直观的线段图作支撑，用“一一对应”的思想找出“点”与“间隔”的关系，从而发现植树问题的本質所在。总之，通过简单的画图来分析数量关系，有助于提高学生解决实际问题的能力。

四、借助图表直观，培养思维能力

数学的本质是数学思想和方法，它具有抽象性的特点，而小学生认识事物带有较大的具体性和直观形象性，他们只有在对具体材料充分感知并理解到一定的程度时才会逐步上升为抽象思维。所以我们可以借助“图”引导学生进行观察，培养学生思考问题的能力。如教学“两个数积一定时，两数之间成反比例”这一抽象关系时，我们可以借助实例来思考问题。如图3所示为面积是12平方米的长方形，让学生思考：长（a）、宽（b）取整米数时，a和b之间的关系。

借助长方形面积一定这个几何模型，学生观察到，当长方形面积固定不变时，宽随着长的变化而变化，长越大，宽就越小，反之亦然。在这里，学生直观地理解了“积一定时，两个乘数成反比例是怎么回事”。同时在画图中还渗透了“有序”“全面”解决问题的思考方法。为此，借助图形引导学生进行自主探究，有效地培养了学生的数学思维。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2]林碧珍.数学思维养成课：小学数学这样教[M].福州：福建教育出版社，2013.

（责任编辑：奚春皓）