无界域上带非线性阻尼和强阻尼随机波动方程解的性态

吴 苑，乔 丹，李晓军

（河海大学 理学院，江苏 南京 211100）

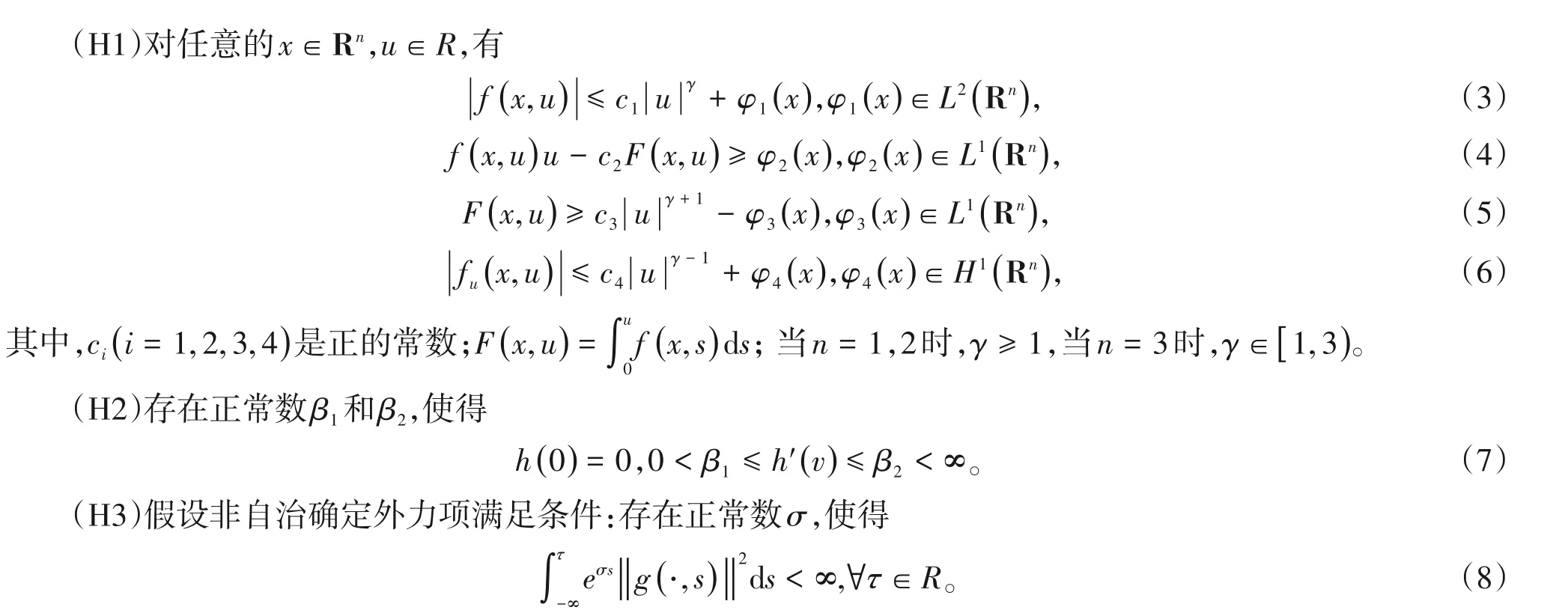
波动方程是一类重要的偏微分方程，具有广泛的物理背景，主要用于描述自然界中各种波动现象，例如声波、光波和无线电波等，为声学、电磁学和流体力学等领域的研究提供了强有力的科学理论依据。目前已有许多学者对波动方程进行了研究，如：文献[1-2]研究了有界区域上自治随机波动方程所确定的随机动力系统随机吸引子的存在性，文献[3-4]研究了带强阻尼波方程吸引子的存在性。文献[5-6]对非自治随机动力系统进行了研究，通过引入两个驱动动力系统，证明了非自治随机动力系统随机吸引子存在的充分必要条件。关于随机波动方程的其他研究参见文献[7-8]。目前还没有文献研究无界域上带有非线性阻尼以及强阻尼的随机波动方程。

本文将研究无界域上带有非线性阻尼以及强阻尼的随机波动方程。在无界域的情况下，由于Sobolev嵌入紧性的缺失，可以利用有界球上的一致估计以及无界域上的尾部一致小估计证明动力系统的渐近紧性，如文献[9]。本文采用对解的一致估计和区域分割的方法来克服Rn上Sobolev嵌入缺乏紧性的困难，即在有界域上对相应的解进行渐近估计，对相应无界域上的解进行一致小估计，并结合解的分解估计得到了该随机动力系统的渐近紧性，进而得到随机吸引子的存在性。

本文中，||⋅||和(⋅,⋅)分别表示L2(Rn)上的范数和内积，||⋅||X表示一般的Banach空间上的范数，字母c表示某一正常数，且其值可能每行各不相同，字母ci(i= 1,2,…)表示特定常数。

1 准备知识

令X是可分的Banach空间，(Ω,F,P)是概率空间，其中Ω ={ω∈C(R,R):ω(0)= 0}，F是Ω上紧开拓扑诱导的Borelσ-代数，P表示(Ω,F)上相应的Wiener测度。定义变换

1）Φ( ⋅,τ,⋅,⋅):R+× Ω ×X→X是(B(R+)×F×B(X),B(X))-可测的；

2）Φ(0,τ,ω2,⋅)是X上的恒同映射；

3）Φ(t+s,τ,ω,⋅)= Φ(t,τ+s,θsω,⋅)∘Φ(s,τ,ω,⋅)；

4）Φ(t,τ,ω,⋅):X→X是连续的。

定义1.4 称K={K(τ,ω):τ∈R,ω∈Ω}∈D是Φ 的D-拉回随机吸收集，若对任意的t∈R+，τ∈R，ω∈Ω，D͂∈D，存在T=T(D͂,τ,ω)> 0，使得对任意的t≥T，有

定义1.5 称A={A(τ,ω):τ∈R,ω∈Ω}∈D是Φ 的D-拉回随机吸引子，若对任意的t∈R+，τ∈R，ω∈Ω，有

1）A(τ,ω)在X上是紧的且A关于F在Ω中是可测的；

2）A是不变的，即Φ(t,τ,ω,A(τ,ω))=A(t+τ,θtω)；

3）A吸引D中的任意集合，即对任意的D͂={D͂(τ,ω):τ∈R,ω∈Ω}∈D，

其中dH是X上的Hausdorff半距离。

定理1[5]令D是X上包含闭的非空子集族，若Φ在X上是D-拉回渐近紧的，且在D上存在一个闭可测D-拉回随机吸引集K，那么，对任意的τ∈R，ω∈Ω，Φ在D上存在唯一的D-拉回随机吸引子A有

2 随机动力系统

本节证明式（1）～（2）的解可以生成随机动力系统，考虑一维Ornstein - Uhlenbeck方程

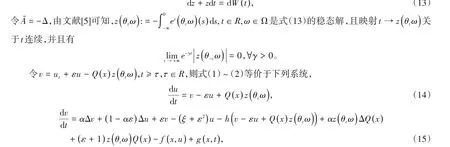
初值为

如同文献[5]中的证明，有如下引理：

引理2.2 令φ(t+τ,τ,θ-τω,φ0)=(u(t+τ,τ,θ-τω,u0),v(t+τ,τ,θ-τω,v0))T，其中φ0=(u0,v0)T，且式（3）～（7）成立，则对任意的ω∈Ω，τ∈R，φ(τ,τ,ω,φ0)=φ0∈E(Rn)，式（14）～（16）在E(Rn)上存在唯一解φ( ⋅,τ,ω,φ0)∈C([τ,+ ∞),E(Rn))，且该解连续依赖于初值φ0，此时式（1）～（2）的解生成连续的随机动力系统Φ:R+×R× Ω ×E(Rn)→E(Rn)，

3 解的一致估计

为证明D-拉回随机吸收集的存在性以及随机动力系统Φ的D-拉回渐近紧性，下面对式（14）～（16）的解进行一致估计。

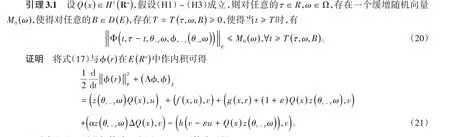
现对式（21）逐项进行估计。应用Cauchy不等式可得

由假设（H3）、式（32）和式（34）可知结论成立。

由上述结论可得以下引理。

引理3.2 设Q(x)∈H1(Rn)，假设（H1）～（H3）成立，则定义在E(Rn)上的连续动力系统Φ(t,τ,ω,φ0)有随机拉回吸收集B={B(τ,ω):τ∈R,ω∈Ω}∈D，其中B(τ,ω)定义为