含裂缝管桩低应变测试的三维数值分析
卢志堂, 程晓东,2, 郭 扬, 柯宅邦, 王 飞, 陶 俊
(1.合肥工业大学 资源与环境工程学院,安徽 合肥 230009; 2.安徽联智工程检测有限公司,安徽 合肥 231200; 3.安徽省建筑科学研究设计院,安徽 合肥 230032; 4.绿色建筑与装配式建造安徽省重点实验室,安徽 合肥 230032)
0 引 言
预应力高强混凝土(prestressed high-strength concrete,PHC)管桩,是在近代高性能混凝土和预应力技术基础上发展起来的混凝土预制构件,目前已经得到了广泛应用,然而在施工过程中,其管壁可能会产生裂缝。文献[1]发现大直径PHC管桩中出现裂缝的概率大多占全部桩基的5%~30%,最大可超过40%,裂缝宽度小的在0.2 mm以下,最大可达50 mm。文献[2-3]指出,管桩中严重裂缝的宽度可超过3 mm。较大的裂缝会降低管桩的承载力,服役期随着地下水的进入,会对内部钢筋造成腐蚀,影响耐久性。因此,精确检测管桩中裂缝,对保障桩基工程安全具有重要的实践意义。
管桩裂缝识别的相关研究工作主要集中在低应变完整性检测方面。文献[4]对PHC管桩各类测试信号的特征进行了探讨和总结;文献[5]通过低应变测试信号的时频分析法与小波分析法处理对比,发现小波分析方法可以更准确地识别细小裂缝的反射波;文献[6]通过对含裂缝管桩的低应变检测实验,发现桩顶速度响应与裂缝倾向密切相关。
上述研究的基础是传统的一维杆理论,而管桩是三维体,低应变测试时,其桩顶承受偏心激振作用,平截面假定已经无法满足,因此,需要采用三维波动理论对管桩低应变测试进行分析。文献[7]研究了尺寸效应对管桩低应变检测的影响;文献[8]探讨了桩顶面不同测点的反射波信号特征及其与桩身裂缝的对应规律;文献[9]分析了现浇薄壁管桩(cast-in-place concrete thin-wall pipe pile,PCC)低应变检测中的三维效应;文献[10-11]采用弹性动力有限积分法(elastodynamic finite integration technique,EFIT)讨论了三维干扰来源,并给出了压制三维干扰的措施;文献[12]分析了管桩中三维波场特征,发现管桩中除纵波外,还存在横波;文献[13]提出了一种考虑横波传播的管桩缺陷定位方法;文献[14]基于简化的解析解,指出三维干扰源于第一阶横截面振动的非对称模式;文献[15]基于简化的解析模型,提出了用于管桩检测的双速度对称叠加法;文献[16]研究了管桩缺陷检测敏感性的影响因素。上述研究大多是针对完整桩开展的,目前针对含裂缝管桩的研究尚不充分。
本文采用EFIT对含严重裂缝管桩的低应变测试进行三维模拟分析;根据建立的管桩低应变测试数值模型,得出桩顶轴向速度响应;分析激振脉冲宽度、裂缝产状(包括横向和轴向)、采样位置、裂缝长度及位置对桩顶轴向速度响应的影响。
1 计算模型
在柱坐标系下建立管桩的低应变测试模型,如图1所示。图1中:h为管桩壁厚;Ro为外圆半径。在管桩壁厚1/2处施加瞬态激振力p(t),其激振区域是以r0为半径的圆。根据低应变条件,可将桩用线弹性模型表征。桩身材料为混凝土,其拉梅系数λ=16 GPa,μ=24 GPa,密度ρ=2 500 kg/m3。
本次模拟仅对自由管桩进行分析,暂不考虑桩周土的影响。
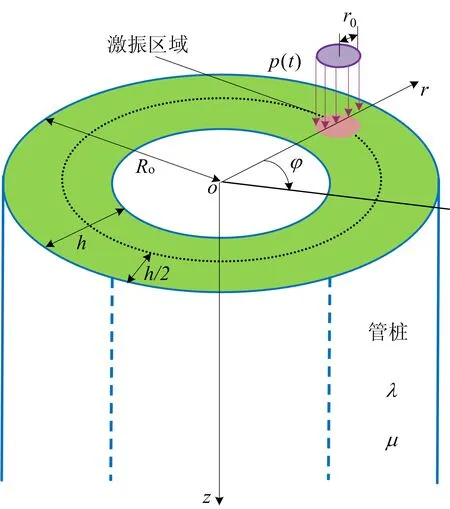
图1 管桩低应变测试计算模型
在柱坐标系中,桩顶轴向应力边界条件为:
(1)
其中,rc=Ro—h/2。用升余弦脉冲函数表示瞬态激振力p(t),其表达式[17]为:
(2)
其中:I为激振力冲量,取1 N·s;t0为脉冲宽度;H(·)为阶跃函数。
2 数值算法
采用EFIT对图1中的管桩进行网格划分,EFIT单元及变量布置如图2所示。

图2 EFIT单元的变量分布
从图2可以看出,应力σij(i或j表示r、z、φ)和速度vi分别定义在不同位置,形成交错网格。
最终得到空间离散方程为:
(3)
(4)
(5)
(6)
(7)
(8)

(9)
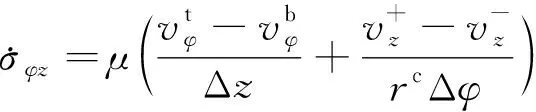
(10)
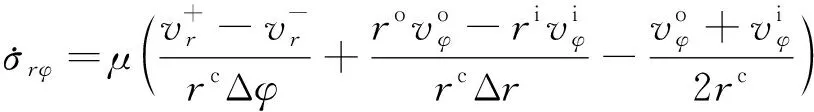
(11)
其中:ri、rc、ro分别为单元内侧、中间及外侧距z轴的径向距离;“+”、“—”分别表示沿φ轴正方向和负方向;t、b分别表示沿z轴的正方向和负方向。
除了在空间上使用交错网格外,在时间上也采用了交错采样,即
(12)
其中,n为时间步数。EFIT的求解流程具体见参考文献[11]。
3 算法验证与结果分析
编写EFIT程序,对裂缝管桩的低应变检测进行模拟分析。管桩尺寸如下:桩长l=7 m,桩身外壁半径Ro=25 cm,壁厚h=10 cm。低应变检测时,通常采用材质不同的锤子敲击桩顶来产生激振脉冲,其中宽脉冲有利于获取桩底或桩身下部缺陷反射信号,而窄脉冲有利于获取桩身上部缺陷反射信号[18]。下文的分析考虑了宽、窄脉冲对桩顶测试结果的影响。
3.1 算法验证
首先对编制的程序进行验证。一根含横向裂缝的管桩照片如图3所示。

图3 横向裂缝布置
图3中,该裂缝距桩顶2 m,由切割锯制成,贯穿壁厚范围。裂缝长度lc=40 cm,宽度wc=0.4 cm。数值模拟时,对完好区,网格参数Δr=1 cm,Δz=5 cm,Δφ=6°;对裂缝区,Δz=0.4 cm。测试时,在缺陷对侧的桩顶激振,采样点与激振点夹角为90°。
实测结果与模拟结果对比如图4所示,图4a和图4b分别由铁锤和尼龙锤敲击桩顶,对应的脉冲宽度t0分别为0.8、1.5 ms。
从图4a可以看出,当窄脉冲激振时,模拟结果与实测结果都有清晰的裂缝导致的一次反射和二次反射,且反射波到时基本一致,仅幅值有一定差异;从图4b可以看出,当宽脉冲激振时,模拟结果与实测曲线中都没有明显的缺陷反射信号。由于测试时管桩平卧在地面上,并非理想的自由桩,会有部分能量传到土中,这会造成模拟结果和实测结果并不能很完美地匹配。但从整体上来看,模拟结果能够反映裂缝对管桩轴向振动速度的作用规律,表明该方法适用于模拟含裂缝管桩的低应变测试。
从图4还可以看出,窄脉冲激振能有效获取横向裂缝反射信号,因此管桩检测需要如铁锤等坚硬材质的激振工具,而尼龙锤的效果很差。

图4 数值结果与实测结果对比
3.2 横向裂缝
首先探讨裂缝宽度wc对桩顶轴向速度响应的影响。考虑1、4、8 mm 3种宽度,其中裂缝宽1 mm的包括40、80 cm 2种长度,其余裂缝长度均为40 cm。裂隙宽度对轴向速度响应的影响如图5所示。
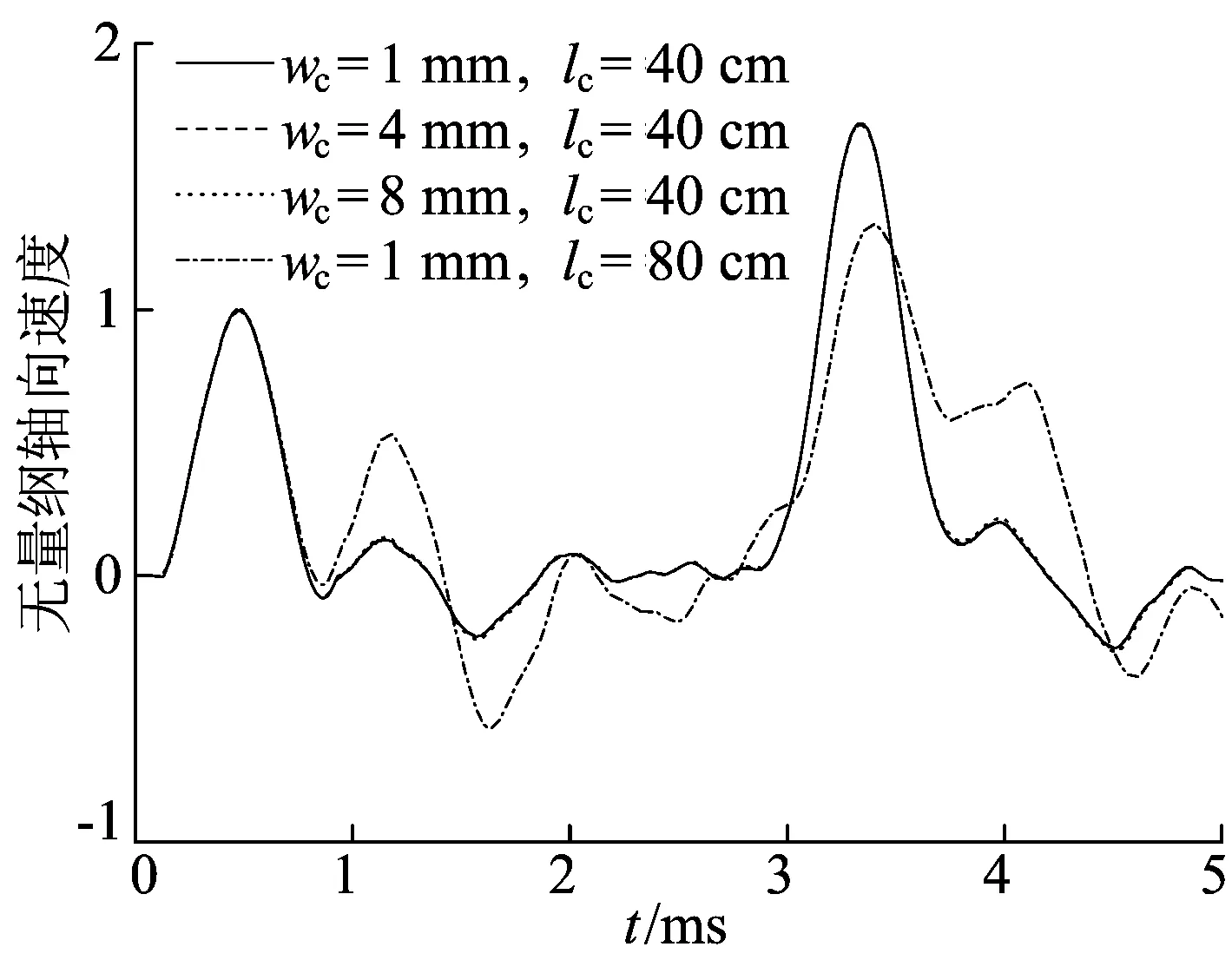
图5 裂缝宽度对轴向速度响应的影响
由图5可知:当wc从1 mm增大到8 mm时,缺陷反射信号基本不变;而对宽度为1 mm的横向裂缝,其长度由40 cm增大到80 cm后,裂缝反射信号显著增强。因此,缺陷反射信号的强度取决于裂缝长度,而非裂缝宽度。
横向裂缝深度dc变化时桩顶轴向速度响应如图6所示。
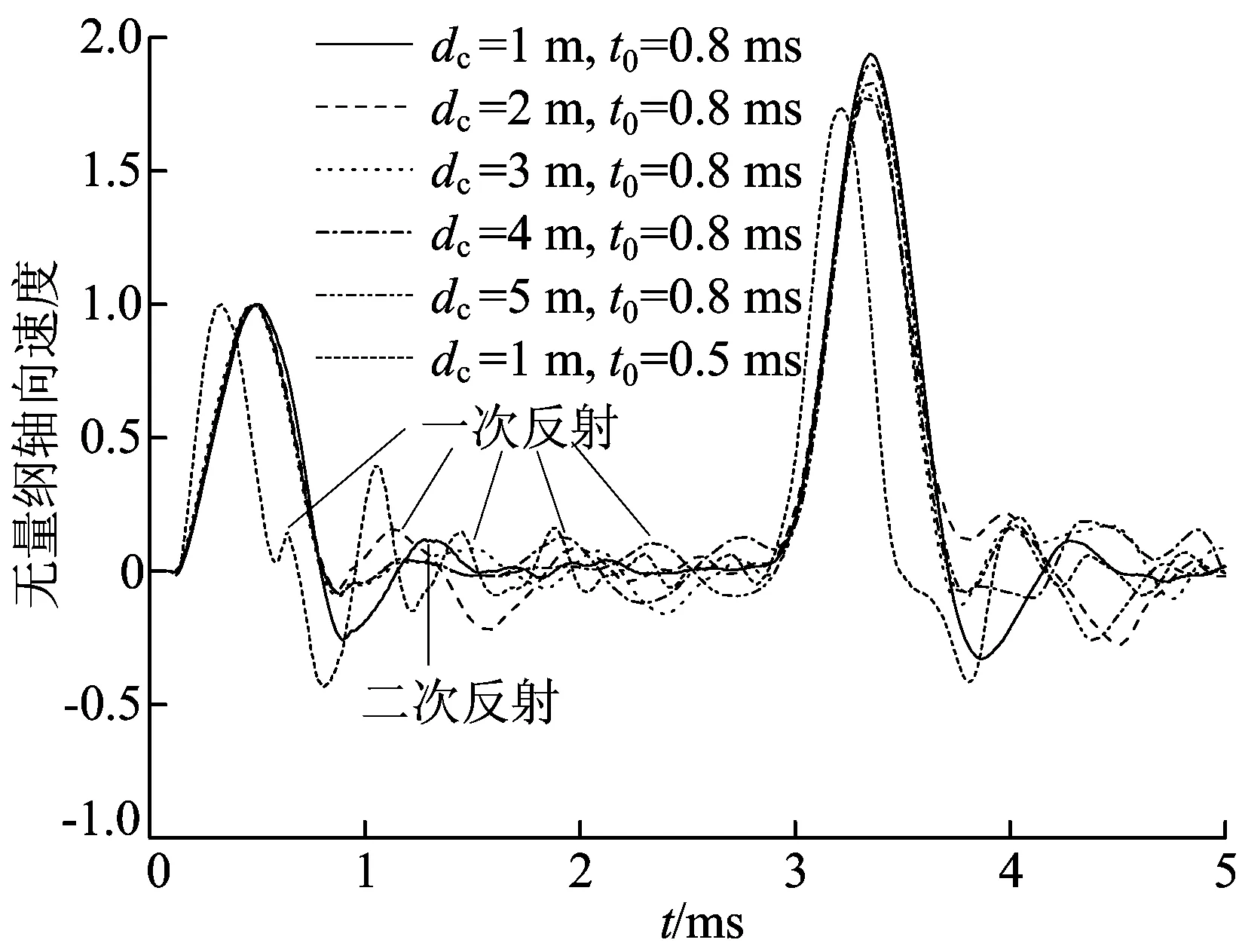
图6 含横向裂缝管桩轴向速度响应
图6中,裂缝尺寸lc=40 cm,wc=4 mm。从图6可以看出,当dc=1 m,t0=0.8 ms时,轴向速度曲线中并没有出现裂缝对应的一次反射,但能够看到二次反射。这是由于缺陷位置距桩顶较近,入射波与裂缝的一次反射波在桩顶叠加,导致一次反射无法辨别。如果仅根据该曲线而不了解桩中裂缝情况,那么可能把二次反射错认为是一次反射,造成误判。当dc≥2 m时,缺陷的一次反射清晰可辨。对于1 m裂缝的识别,需要更窄的脉冲避免叠加效应的影响。
图6给出了t0=0.5 ms时的轴向速度曲线,此时一次反射与入射波的叠加效应明显变弱,因此曲线变得清晰。
另外,缺陷的位置也是低应变检测关注的问题之一。根据一维波动理论,桩身杆波波速C为:
C=2l/ΔT
(13)
其中,ΔT为入射波峰与桩底反射波峰之间的时间差。缺陷位置dc′为:
dc′=CΔtc/2=lΔtc/ΔT
(14)
其中,Δtc为反射波峰与入射波峰之间的时间差。裂缝位置分析结果见表1所列。表1中,ξ为相对误差。当dc=1 m,t0=0.8 ms时,轴向速度曲线中没有出现裂缝对应的一次反射,无法计算裂缝位置,因此表1中无相应结果。
由表1可知:由一维理论计算出的缺陷位置比实际位置浅;随着裂缝深度增大,相对误差逐渐降低。实际上,激振点与采样点相差90°,入射波(主要为瑞利波)从激振点沿环向传至采样点会产生滞后时差[12-13],而一维理论忽视了时差影响,导致计算出的裂缝位置偏浅。本文提出一种考虑时差ΔtI的修正方法。ΔtI计算公式为:
(15)
其中,CR为瑞利波的波速。

表1 裂缝位置分析结果
对本文中的管桩模型,根据瑞利波与剪切波速的关系[19],可以得出CR=0.91Cs=2 819 m/s,其中Cs为剪切波速,计算公式为:
(16)
修正后的波速为:
(17)
(18)
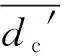
(19)
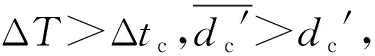
3.3 轴向裂缝
轴向裂缝也是常见的管桩裂缝类型之一,下面对含轴向裂缝管桩的测试进行模拟,其中裂缝区Δφ为1.1°,计算结果如图7所示。
图7a所示为不同长度轴向裂缝对应的竖向速度响应,以及含横向裂缝桩和完整桩的模拟结果,其中wc=4 mm,裂缝顶端距桩顶2 m。从图7a可以看出:轴向裂缝桩的轴向速度曲线与完整桩几乎一致,需要注意的是,完整桩所对应曲线中的入射波和桩底反射波之间震荡为三维干扰波[11];而横向裂缝桩的模拟曲线中有明显的裂缝反射波。
图7a结果表明,低应变反射波法不能用于探测轴向裂缝。为进一步证实这一点,图7b给出了不同激振-采样组合方式得到的轴向速度曲线,其中裂缝长度仍为40 cm,顶端距桩顶2 m。上述模拟中,激振点均在缺陷对侧,并与采样点夹角为90°,即图7b中的C-B组合方式,由图7b可知,采用B-A,B-C及A-B组合方式时,仍然很难从轴向速度曲线中看出明显的裂缝反射波。

图7 含轴向裂缝管桩轴向速度响应
4 结 论
本文采用EFIT对含裂缝管桩的低应变测试进行了三维数值分析,探讨了激振脉冲宽度、裂缝产状、裂缝长度及位置对桩顶轴向速度响应的影响,得到如下结论:
(1) 含横向裂缝管桩的低应变测试结果与数值模拟结果一致,表明EFIT适用于含裂缝管桩低应变测试的模拟分析。
(2) 窄脉冲激振时,低应变反射波法可以识别管桩中的横向裂缝,但根据一维理论得到的裂缝位置比实际偏浅,随着裂缝深度增大,相对误差会逐渐降低。本文提出的定位修正方法考虑了激振点与采样点之间的时差,能够提高裂缝位置的探测精度。当横向裂缝位置较浅时,需要更窄脉冲激振,否则可能将二次反射错判为一次反射,即使进行修正,得出的缺陷位置也是不准确的。
(3) 对含轴向裂缝管桩低应变测试的模拟结果表明,仅依靠轴向速度响应,无法识别管桩中的轴向裂缝。
需要指出的是,本文数值模型中的裂缝宽度较大(4 mm),但实际管桩中裂缝的宽度可能小于该数值,因此本文的结论对开裂程度较大管桩的检测更有参考价值;此外,本研究没有考虑桩周土对测试结果的影响,这将在后续研究中加以考虑。

