基于FLAC的路基边坡稳定性分析
杨帆

摘 要:科学准确的边坡稳定性分析是路基边坡防治加固的重要决策依据,针对传统路基边坡稳定性分析方法存在误差大、效率低下等弊端,本文梳理总结了提高路基边坡稳定性分析结果精确性的技术要点,基于FLAC仿真软件从主应力云图、位移云图和稳定性系数三个方面对构建的高边坡仿真模型进行了计算与分析,据此系统评估了边坡稳定性,为路基边坡防治加固提供借鉴与参考。
关键词:FLAC模型;路基边坡;稳定性;仿真分析
中图分类号:U416.14 文献标识码:A
0 引言
路基边坡稳定性关系着整个公路的耐久、稳定与安全,边坡坡度、地质岩性、地质结构、地下水发育情况以及施工等因素均对边坡稳定性造成重要影响,而传统路基边坡稳定性分析方法存在误差大、效率低下等弊端[1-3],故有必要运用科学合理的路基边坡稳定性分析方法,进一步确定合理的路基边坡构型,为路基边坡防治加固提供借鉴与参考。
1 路基边坡稳定性分析概述
传统路基边坡稳定性分析方法存在误差大、效率低下等弊端,为保证路基边坡稳定性分析结果精确性,科学掌握斜坡的自然环境、地形和地质参数,以及合理运用匹配计算方法和参数指标尤为重要[4-6]。
1.1 参数值的合理化
路基边坡稳定性分析需要考虑选取参数的合理性,相关分析显示,计算方法在对边坡稳定性的评估方面实际影响相对较小,但由于斜坡土本身存在不均匀的特性,其参数值选取的变化性必会对计算结果造成偏差,因此如何合理优化计算参数是未来研究重点。
1.2 分析方法的组合
目前尚未存在一种可以完全解决和分析所有问题的方法,将两种或更多种方法结合起来相互融合运用是未来的发展趋势。如对专家系统进行分析与设计时,可以利用遗传算法进行推导和设计,并对函数选择以及相关参数进行确定;另外,可充分组合利用有限元、离散元,数值解、解析解的组合等各自优势解决较为复杂的梯度问题。
1.3 系统理论
路基边坡是复杂的开放系统,故综合考虑各个子系统之间的相互作用和联系,并利用控制论和协同学等理论来稳定边坡,据此研究和分析机制特性也是研究趋势之一。
1.4 反分析方法运用
目前多依据梯度应力来研究梯度系统的不稳定性,若反向思维考虑,则可以从梯度系统的变形分析中获得对梯度稳定性的分析,并进行稳定性评估。例如,反位移分析的方法是基于测得的位移值的反演获得初始应力和参数,然后将其应用于工程实践。
2 FLAC程序简介
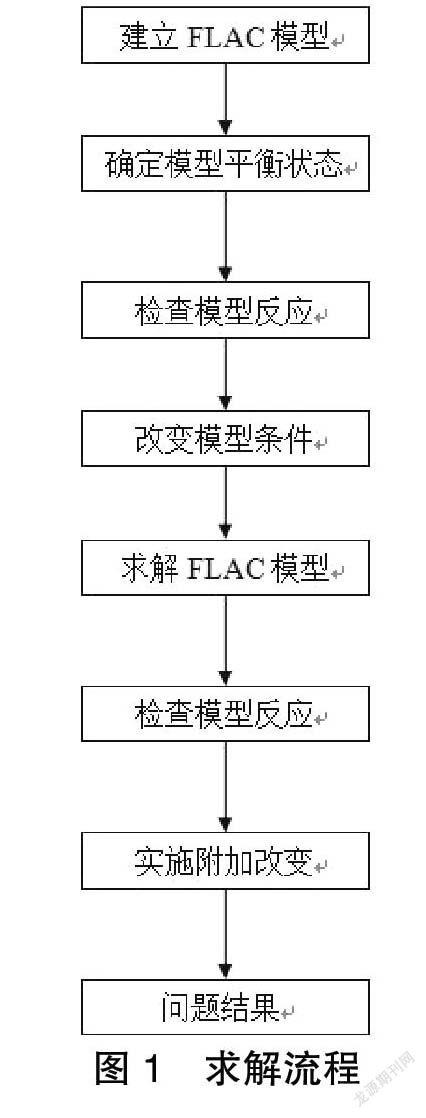
上述概述可知,合理运用计算方法对保证路基边坡稳定性和安全性分析结果精确性尤为重要。FLAC软件基于拉格朗日差分法构成,允许计算过程中材料的屈服和流变以模拟地面岩土所具有的力学属性,故更适合解决模拟较大变形及扭曲,具有综合性,速度性和经济性等优点[7-8],其相关计算流程如图1所示:
3 公路路基边坡稳定性分析
3.1 FLAC模型建立
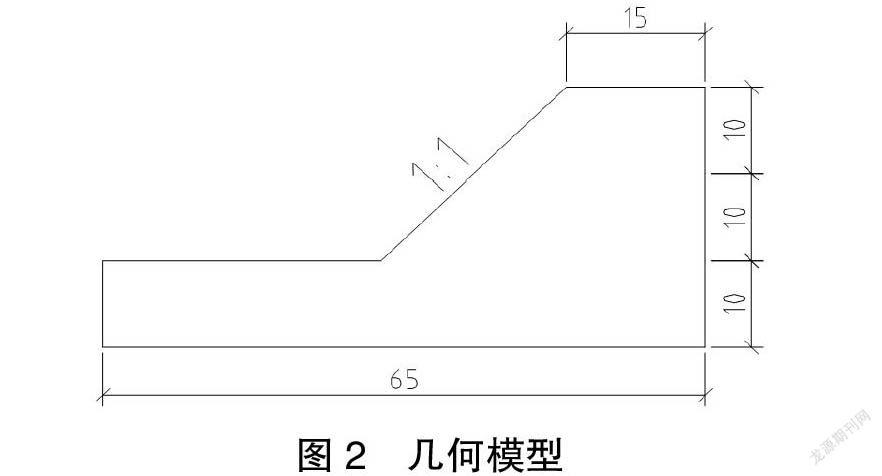
某一级公路路基设计宽度为30 m,边坡设计坡度为1:1。路基土体分为三层,基层为粘土,层厚10 m;中层为硬粘土,经压实,层厚10 m;上层为中细沙土,层厚10 m;路基底部宽100 m。
建立几何模型如图2所示:
FLAC的边界条件限定为限制节点位移,假设路基中心线左右各材料性质完全一致,中心线左右受力及位移正对称,据此确定边界约束条件为:地基土的下部边界视为无位移的固定边界,中心对称面和侧面各节点限制水平位移。
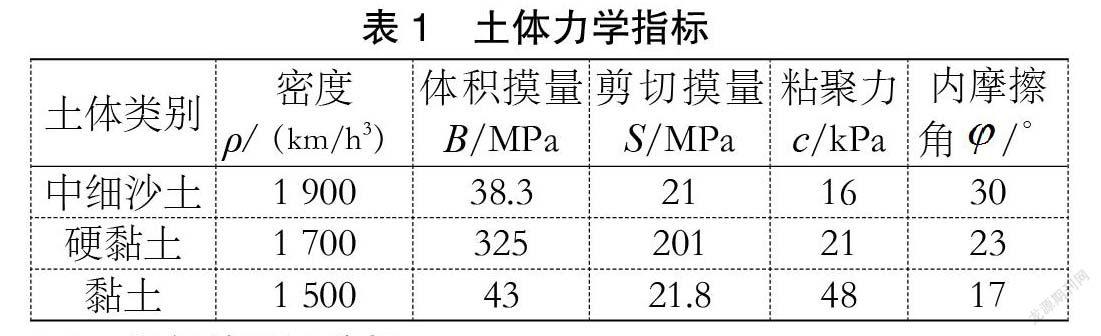
本文采用Mohr-Coulumb模型对边坡稳定性进行模拟计算,此模型计算效率较高,适用于松散状和黏结状的粒状散体材料,如土体、岩石、混凝土等。主要参数指标有:岩土体弹性模量E、泊松比v、剪胀角ψ、体积模量B、剪切模量S等均对稳定性分析结果造成影响。每个土壤层的物理和机械参数如下表1所示:
3.2 运行结果及分析
运行FLAC软件自动完成仿真,获取主应力云图、位移云图和稳定性系数,可依次对边坡进行应力分析,位移分析和变形分析,据此评估边坡的稳定性。
3.2.1 应力分析
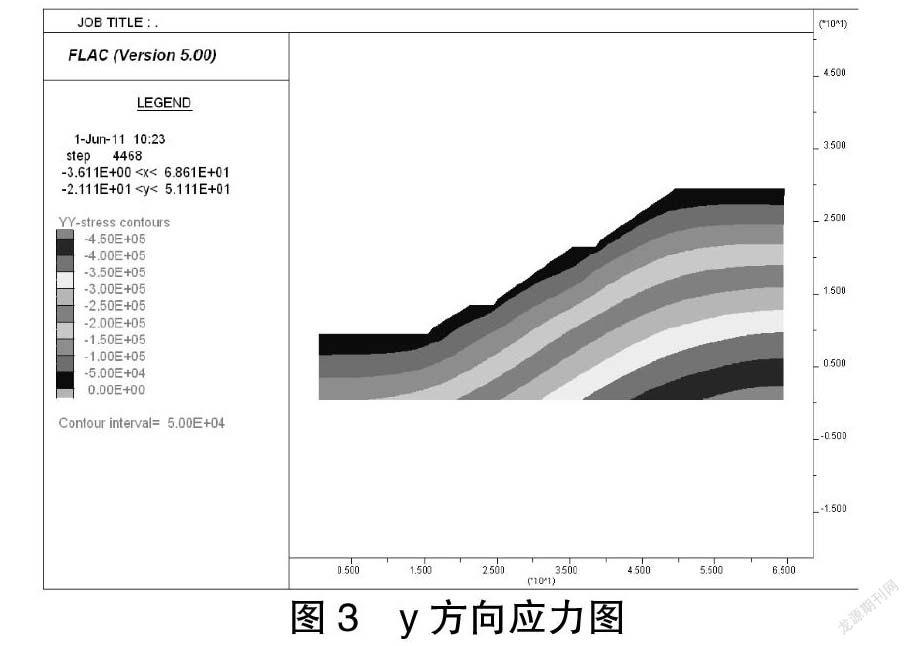
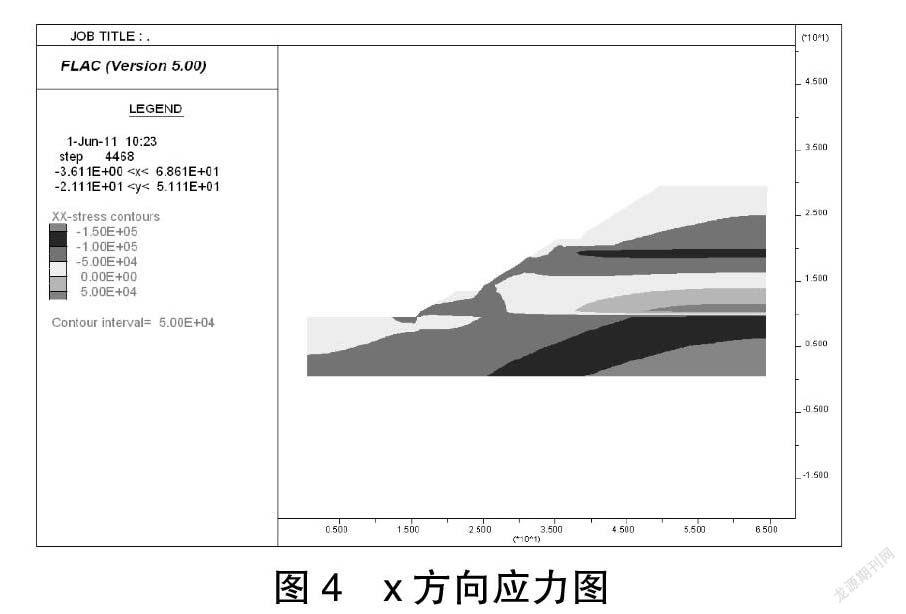
输出的主应力云图如下图3、4所示。
图3和图4是FLAC中的模拟应力云,分析上图可知,显示y方向上的垂直应力是压应力,随着土壤厚度的增加而增加,并且与场应力的变化一致。斜率周期性地从外到内逐渐增大,其应力值达到最小值或零,从其顶部到底部逐渐增大,并且应力达到最小值或零。x方向的侧向应力有规律地分布在倾斜体上,并且随着倾斜轴承的增加,最大压应力值为150 kPa。拉应力也出现在倾斜的顶面下方的某些深度(下部中心)。路基斜坡的特征是在横向方向上受拉和受压,主要是受压,但在垂直方向受压。
3.2.2 边坡位移
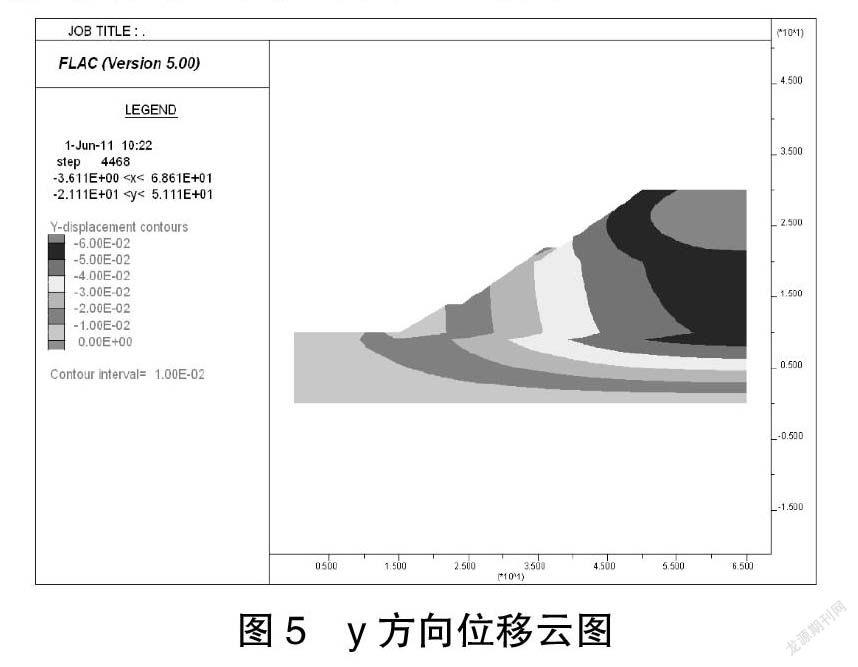
输出的位移云图如下图5、6所示。
图5和图6分别是斜率的垂直位移图和横向位移图,分析上图可知,较低坡度在y方向上的最大位移达60 mm,发生在较低坡度的中心表面附近。随着土壤层厚度的增加,位移值逐渐减小,直到可以忽略不计或为零。与原始路基设计斜坡相比,斜坡上没有形成最大位移区域,这使斜坡变慢,从而有助于分散應力。x方向上的最大位移发生在倾斜轴承内部,最大位移值为7.5 mm。与原始路基设计坡度相比,最大位移区域从坡度附近的坡度移动到坡度内部以创建拐角。倾斜不会导致倾斜体的整体减小。与原始线性斜率相比,y和x方向上的阶跃斜率的位移值分别减小了65.7%和94%。
3.2.3 稳定系数
FLAC软件运行完成之后,由数值模拟的结果分析可知,稳定系数数据结果为1.58~1.59,边坡稳定。
综上,基于FLAC仿真软件构建土壤土质高边坡模型进行计算与分析,斜坡形状从直线线性改变为折线线性,即设置台阶后y和x方向上的阶跃斜率的位移值分别减小了65.7%和94%,且稳定系数数据结果为1.58~1.59,边坡稳定。
4 结语
基于主应力云图、位移云图和稳定性系数三个方面对构建的高边坡仿真模型进行了计算与分析,斜坡形状从直线线性改变为折线线性,即设置台阶后y和x方向上的阶跃斜率的位移值分别减小了65.7%和94%,且稳定系数数据结果为1.58~1.59,边坡稳定。为路基边坡防治加固提供借鉴与参考。
参考文献:
[1]张宝龙,范文.土-岩混合边坡的破坏模式研究[J].公路交通科技,2018(4):33-39.
[2]吴忠广,申瑞君,万福茂,等.岩质高边坡运营安全风险源辨识方法[J].公路交通科技,2018(3):8-15+27.
[3]高连生,赵炼恒,李亮,等.带台阶的多级边坡稳定性上限分析[J].公路交通科技,2014(6):1-10+22.
[4]张圣东.高边坡整体稳定性分析研究[J].黑龙江交通科技,2020(3):39-41.
[5]袁冬艳,张太乐,彭大江,等.山区路基边坡稳定性分析及生态防护[J].住宅与房地产,2019(36):183.
[6]杨敏,方诗圣,张云峰.期望成本最优的土质高边坡坡角设计研究[J].工程与建设,2016(1):5-8.
[7]陈海.基于FLAC3D的陡坡路基不均匀沉降控制措施分析[J].山东交通科技,2020(1):76-79.
[8]李汉锋.基于FLAC3D的土质路基边坡动力响应规律研究[J].公路交通科技(应用技术版),2019(7):87-89.

