基于9种无约束优化算法的岩爆预测BP模型优选

王 超，李岳峰，邵 琳，张亚平，徐健珲，王航龙

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，云南 昆明 650093）

0 引言

岩爆是工程开挖时岩石破坏造成失稳并伴随着能量猛烈释放的一种地质灾害，随着地下工程逐步向深部发展，岩爆对矿井、隧道、水电硐室等工程的安全生产威胁愈发严重［1］.如：2014年3月9日，云南独龙江隧道发生岩爆，3名施工人员遇难；2015年5月31日，巴基斯坦N-J水电站引水隧洞发生的岩爆导致3人死亡17人受伤.准确预测岩爆烈度等级是防控岩爆的有效手段.由于岩爆机理复杂、致因众多，考虑多指标的综合预测模型在岩爆预测中发挥了重要作用［2-5］.

BP（Back Propagation）神经网络通过逐层修改权值、逐步减小误差直至最小，从而完成网络训练.修改权值有不同规则即不同的无约束优化算法.针对标准BP算法（梯度下降法）存在收敛速度慢、产生局部极值、训练易瘫痪、难以确定隐层节点等问题，众多学者采用不同的无约束优化算法建立了BP神经网络模型：文献［6-8］采用动量法结合自适应学习率方法改进了BP网络模型并进行了工程应用；李永松等［9］采用Levenberg-Marquardt算法优化BP神经网络，减小了训练中的计算量和内存需求量；王斌等［10］在网络中加入动量项，并引入新的训练方法Rprop（Resilient BP）进行优化，提高了网络的可靠性；张强［11］采用粒子群算法（Particle Swarm Optimization，PSO）优化了网络初始权值和阈值，避免了神经网络陷于局部最优值；孙臣生［12］基于有动量的梯度下降法改进了算法模型，工程应用准确有效.综上，现有研究多采用某种无约束优化算法对标准BP神经网络模型进行改进，并取得了良好效果，而基于不同无约束优化算法的优化效果对比分析尚需开展系统研究.

鉴于此，本文选取9种典型的无约束优化算法，对比研究训练样本数量分别为40、70和100时的不同优化算法对BP神经网络预测准确率的影响，优选出最佳岩爆预测模型并进行工程应用.

1 无约束优化算法选取

本文主要研究用于岩爆烈度等级预测的BP神经网络模型的无约束优化问题，即在无约束条件下，如何取值才能获得BP模型的最优预测效果.因此，选取具有代表性的9种无约束优化算法作为标准BP神经网络的改进算法，即：共轭梯度法、Fletcher-Reeves共轭梯度法、Ploak-Ribiere共轭梯度法、最小均方误差算法（Least Mean Square（LMS）algorithm）、动量梯度下降法、自适应lr梯度下降法、自适应lr动量梯度下降法、Levenberg-Marquardt算法和拟牛顿算法.这9种算法可采用Matlab神经网络工具箱中相应的训练函数调用，其原理及优点不再赘述，详见文献［9，12-15］.

2 岩爆样本分析

综合考虑预测指标的科学性、实用性、可量化性等因素，选取围岩最大切向应力与岩石单轴抗压强度比σθ／σc、岩石单轴抗压强度与单轴抗拉强度比σc／σt和弹性能量指数Wet作为岩爆烈度等级的预测指标，并对指标开展相关性分析，结果见表1.可见，三个指标两两之间相关性极弱甚至不相关，表明样本选取科学有效.参考国内外大多数学者采用的分级标准，本文将岩爆烈度等级分为Ⅰ级（无岩爆）、Ⅱ级（弱岩爆）、Ⅲ级（中度岩爆）和Ⅳ级（强烈岩爆）.为提高网络的泛化能力，本文查阅相关文献［16-20］，筛选收集了100组烈度等级明确的典型岩爆实例样本，建立了岩爆预测模型的训练样本库，其中Ⅰ～Ⅳ级的岩爆样本数量分别为19、27、36和18，部分样本数据见表2.图1所示为岩爆预测指标的小提琴图，该图结合了箱形图和核密度图的特征，显示了样本数据的分布形状、中位数、四分位数范围、置信区间等数据分布及样本数据出现的频率大小（阴影部分）.

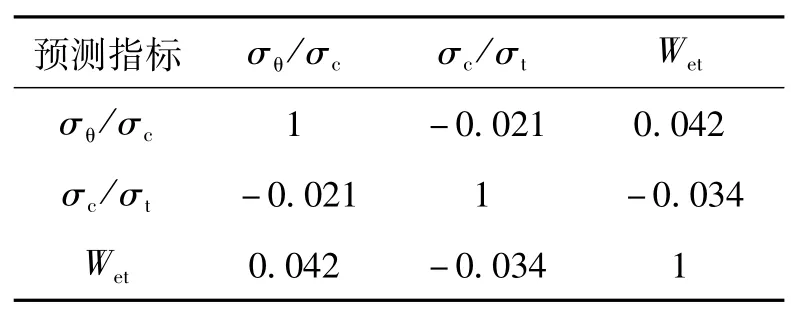
表1 预测指标相关性矩阵Tab.1 Correlation matrix of prediction index

表2 部分样本数据 Tab.2 Part of training samples

图1 预测指标的小提琴图Fig.1 Violin diagrams of prediction indexes

3 岩爆预测模型的建立及优选

3.1 不同样本数量下的预测准确率比较

基于BP神经网络的标准算法（梯度下降法）和9种无约束优化算法，分别建立岩爆预测模型（模型编号为0＃～9＃）.图2所示为不同样本数量下10种BP模型的预测准确率，所有模型在样本数量为100时的预测准确率均比样本数量为40时的准确率大幅提高.计算得到样本数量为40、70和100时的10种模型的平均预测准确率分别为62.5%、76.4%和87.5%.可见，随着样本数量的增加，BP神经网络模型的预测准确率也随之提高.

图2 不同BP模型预测准确率Fig.2 Prediction accuracy of different BP models

3.2 不同优化算法下的预测准确率比较

由图2可知，在样本数量为100时，标准BP模型（0＃模型）的预测准确率仅为71.0%，而9种优化模型中的8种模型的准确率均高于标准BP模型（平均准确率为89.3%，最高为99.0%）.

为了更好地衡量模型的预测准确率，考虑不同样本规模的影响，综合同一模型不同样本数量的多次实验，本文提出一个岩爆烈度等级预测指数——综合准确值N，其大小反映了同等条件下不同模型的预测准确数目.N值越大，模型预测准确率越高.N记为：

式中：Ni为第i种样本规模时该模型预测准确的样本数目，n为样本规模的种类数（本文中的样本规模包括40、70和100，故n＝3）.

计算10种训练方法下的综合准确值N并排序，见表3，表中同时列出了100个样本下的各模型预测准确率的排序.

表3 不同模型的综合准确值Tab.3 Comprehensive accurate values of different BP models

由表3可知，基于9种优化算法建立的BP模型的综合准确值N均高于标准BP模型.将N值排名前两位的模型信息列于表4中.N值最高的为“3＃模型”，即基于Ploak－Ribiere共轭梯度法优化的BP神经网络模型（简称“优选模型①”），其次为“8＃模型”，即基于Levenberg－Marquardt法优化的BP神经网络模型（简称“优选模型②”）；这两个模型在100个样本下的预测准确率同样位列前两位（分别为99.0%和97.0%）.

表4 两个优选模型的预测准确率Tab.4 Prediction accuracy of two optimal models

4 工程应用

为了验证优选模型的工程应用效果，将“优选模型①”和“优选模型②”应用于马路坪矿（1＃实例）［18］、冬瓜山铜矿﹣730水平（2＃实例）［19］、锦屏二级水电站3+390工作面（3＃实例）［19］、秦岭隧道（4＃实例）［19］和秦岭终南山公路隧道（5＃实例）［20］等5个工程实例中，并和基于相同训练样本建立的标准BP神经网络模型及支持向量机（SVM）模型的预测结果进行对比分析，结果见表5.由表可见，“优选模型①”在5个工程应用中表现优良，预测结果与实际等级完全一致；“优选模型②”和标准BP神经网络模型均将2＃实例的岩爆实际等级由Ⅲ级预测为Ⅱ级；SVM模型则将2＃实例由Ⅲ级预测为Ⅱ级，将4＃实例由Ⅲ级预测为Ⅳ级.综合两个优选模型的预测准确率和工程应用表现，确定“优选模型①”即基于Ploak-Ribiere共轭梯度法优化的BP神经网络模型为本文优选的最佳模型.

表5 工程实例预测结果Tab.5 Prediction results of engineering cases

5 结论

1）基于标准算法和9种无约束优化算法分别建立10种岩爆BP神经网络预测模型，其在训练样本数量为40、70和100时的平均预测准确率分别为62.5%、76.4%和87.5%，表明BP模型的预测准确率随样本数量增加而提高.

2）提出了考虑不同样本规模影响的岩爆烈度等级预测的新指数——综合准确值N，计算结果表明基于9种优化算法建立的BP模型的N值均高于标准BP模型.

3）综合9种改进模型的预测准确率和工程应用表现情况，优选出基于Ploak-Ribiere共轭梯度法优化的BP神经网络模型为岩爆烈度等级预测的最佳模型.