相位型光栅的衍射及分光功能

邹意蕴，林佳丽，卢悦媛，阎晓娜

(上海大学 理学院物理系，上海 200444)

光栅是一种重要的分光元件，它通过对入射光的振幅或相位进行调制实现分光功能，在光纤通信和分光光谱仪中具有广泛的应用. 我们在大学的光学课程中主要学习了平面振幅型光栅的衍射，了解到光栅的分光功能是发生在高衍射级[1]. 但在平面振幅型光栅衍射中，不具备分光功能的0级衍射是最强的，它占了入射光能的很大一部分，其余光能量则分散在各高级光谱中，而实际使用光栅时往往只利用它的某一级光谱. 由于光能量分散，各级光谱强度就比较弱，这对光栅应用很不利，因此如何把衍射光能集中于某一具有分光功能的高衍射级次是实现光栅应用的关键. 目前常用的方法是利用闪耀光栅[2]和体全息光栅[3]. 本文提出利用相位型光栅来实现该功能. 相位型光栅是对入射光场的相位进行调制的器件，相比于振幅型光栅来说, 由于它没有不透光缝对光的散射, 因此具有更高的衍射效率. 前期, 高华等人已讨论过相位光栅的透射光谱[4]，谢莉莎等人讨论了具有正弦分布的超声相位光栅的衍射[5]，但他们是基于傅里叶变换的思想来推导衍射光场，对于没有学习过傅里叶光学或信息光学的同学来说可能不清楚该方法隐含的物理意义，难以掌握. 通过光学课程的学习，我们已经知道衍射即是干涉，已有多人利用干涉的相干叠加思想推导了光栅的衍射，如曹驰宇等人利用矢量叠加法推导了缝宽周期性变化的光栅的衍射光强分布[6]；陈学文等人利用旋转矢量法推导了光栅衍射公式[7]；黄时中等人利用实函数积分导出了光栅衍射[8]；张永梅利用光栅衍射是单缝衍射和多缝干涉综合作用结果的思想推导了多圆孔的夫琅禾费衍射[9]. 本文基于相干叠加，即复振幅叠加的思想对相位光栅的衍射公式进行推导，并研究实现光能从0级到±1级转移的光栅参数条件.

1 相位型光栅结构及衍射场推导

图1(a)是本文讨论的透射相位型光栅及其分解图，其中灰色部分代表相位缝, 白色部分代表透光缝. 相位缝由相位材料组成, 对入射光场引入相位. 由于相位光栅中的相位缝和透光缝对入射光都有衍射，为了简化分析，把相位型光栅分解为纯相位光栅和纯振幅光栅的叠加. 其中纯相位光栅只包括相位缝, 原相位光栅中的透光缝用黑色的不透光缝代替；而纯振幅光栅只包括透光缝，原相位光栅中相位缝用不透光缝代替. 相位型光栅的衍射可以看作是分解后的两个光栅衍射光场的相干叠加, 因此下面分别对两个光栅的衍射进行推导.

图1 相位型光栅的结构及分解后光栅的衍射

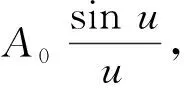
(1)

整理后得到纯相位光栅在P点的复振幅为

(2)

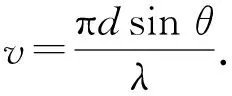
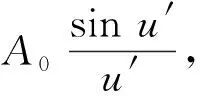
(3)

整理后得到纯振幅光栅衍射的复振幅为

(4)

纯相位光栅和纯振幅光栅中衍射角相同的衍射光通过透镜后会聚到焦面上同一点P, 因此相位型光栅总的衍射场是上述两个衍射的复振幅叠加

Ap=Ap1+Ap2

(5)

对复振幅求模值平方得到相应的衍射光强

Ip=|Ap|2

(6)

下面基于衍射光强公式研究相位型光栅的衍射.

2 相位型光栅的衍射及随光栅参数的变化

设相位型光栅的入射光是He-Ne激光，波长为632.8 nm. 光栅常量d=a+b=2b，缝数N=5，相位层为折射率n=1.5的玻璃材料.图2给出了相位层引入的相位φ为nπ/6，这里n=1,2,3,4,5,6(相应的厚度h分别取0.035 μm，0.070 μm，0.105 μm，0.141 μm，0.176 μm，0.211 μm)时，相位型光栅的归一化衍射光强随衍射角正弦的变化.

图2 归一化衍射光强随衍射角正弦的变化

由图2可见，当相位缝和透光缝宽度相等时，随着相位层引入的相位φ的增加，0级衍射光强逐渐减小，而±1级衍射光强将逐渐增大；当φ增加到π时，0级衍射光强接近0，而±1级衍射光强达到最大值.很显然，相位材料引入的相位φ对衍射光强有调制作用，这可由相干叠加条件来解释.由第一节讨论可知相位光栅的衍射是式(2)和式(4)所描述的两个衍射场的相干叠加.根据双光束相干叠加条件可知，当两个场同相时，叠加强度为极大值；当两个场反相时，叠加强度为极小值；若两个场的相位差介于0和π时，叠加强度将介于极大和极小值之间[1].由式(2)和式(4)可见两个场的相位差与φ有关，所以φ的变化对衍射强度有影响.由图2进一步发现，±2级缺级,φ=π时±3级及高衍射级(这里未全部显示)的衍射光强远远小于±1级衍射,即入射光能量大部分集中在±1级.由此可见，通过改变相位层材料引入的相位可以改变两个叠加光场的相位差，从而实现能量从0级到1级的转移.另外,图2是在d=2b情况下得到了±2级缺级，可见相位型光栅的缺级条件与振幅型光栅的相同.相位型光栅±1级衍射光强大于0级，从这点来说相位型光栅性能优于振幅型光栅.

由以上讨论可知,改变相位层引入的相位可以改变±1级衍射光强,下面进一步讨论相位层引入的相位及光栅占空比对± 1级衍射光强影响.

定义相位型光栅± 1级的衍射效率为

(7)

其中I+1和I-1分别代表正、负一级衍射光强，二者是相等的.Ip代表相位型光栅的总衍射光强.

图3是+1(或-1)级的衍射效率相对于相位型光栅的占空比a/b和相位层引入的相位φ之间的三维关系曲线. 由图可见，占空比和引入的相位都对衍射效率η有影响. 当占空比过大或过小时，±1级衍射效率随相位φ变化不明显；对于确定的占空比，±1级衍射效率都随相位φ的增加而增大. 当相位φ增加到 π 时，能得到最大衍射效率的占空比为1. 即当占空比为1(即相位缝和透光缝宽度相等)、相位层材料引入的相位φ为π时，±1级的衍射效率是最大的，都约为42%，为式(4)所表示的纯振幅光栅±1级衍射效率的4倍. 由此可见，本文提出的相位型光栅的衍射效率是很高的.

图3 +1(或-1)级的衍射效率随占空比a/b和相位层引入的相位φ 的变化关系

3 相位型光栅的分光功能

根据上面的讨论可知，当相位型光栅的相位缝和透光缝宽度相等、且相位层引入的相位φ= π(此时相位层厚度h=0.211 μm)时，±1级的衍射效率是最大的，下面讨论在此情况下相位型光栅的分光功能.

取波长分别为632.8 nm、514.5 nm、440 nm的红、绿、蓝3种颜色的复色光入射到此厚度的相位型光栅，设光栅透光缝N=51. 图4是复色光入射相位型光栅的衍射示意图. 讨论中假设入射时各波长的入射光强相等. 由图可见，不同波长光的衍射位置在0级是重合的，而在±1级是不重合的，即在±1级实现了分光功能.

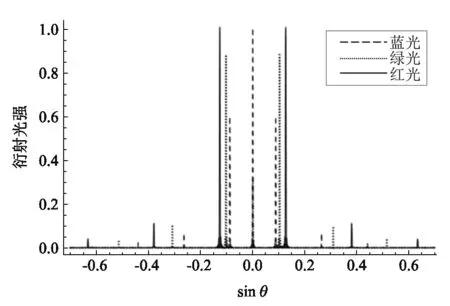
图4 不同波长单色光的衍射光强分布(h=0.211 μm)

对图4进一步研究发现，3种波长的1级衍射光强相差较大，且蓝光的0级衍射比±1级衍射还大些，原因是h=0.211 μm的选择是针对红光而言的，对其他波长的光束来说该厚度不能满足±1级获得极大值条件. 为使不具有分光功能的0级衍射强度尽可能小，而使±1级衍射强度尽可能大且近似相等，下面讨论如何寻找合适的相位层厚度h.

为使±1级衍射光强尽可能大，那么0级衍射光强应尽可能小. 为保证3种波长入射时的0级衍射都尽可能小，考虑使3种波长入射时0级衍射的总光强要小. 图5是红、绿、蓝三种波长光的0级衍射光强的总和随相位层厚度h的变化曲线.

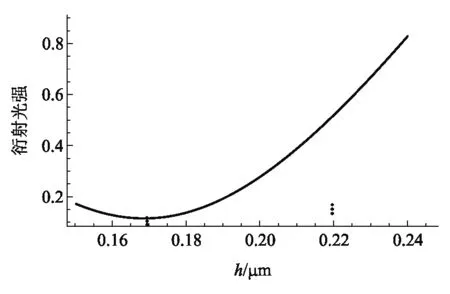
图5 三种波长0级衍射总光强随相位层厚度h的变化

由图5可见，当h=0.169 μm时0级衍射总光强得到极小值. 选择该厚度作为相位型光栅的厚度，图6是复色光入射该光栅时的归一化衍射光强随入射角正弦的变化曲线，可见3种波长光的±1级衍射光强相差不大，且远大于0级衍射光强，此时相位光栅的分光效果是最理想的.

图6 3种波长单色光的衍射光强分布(h=0.169 μm)

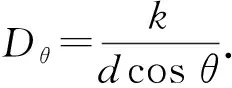
图7 相位光栅的衍射

图8可进一步说明两类光栅的色散率是相同的. 图中虚线代表相位光栅的衍射，实线代表图1(c)所示的振幅光栅的衍射. 由图可见，同一波长所对应的±1级极大值所在的位置是相同的.

图8 相位光栅和纯振幅光栅对3种波长单色光的衍射(虚线和实线分别代表相位光栅和振幅光栅的衍射)

4 结论

本文利用相干叠加, 即复振幅叠加的思想推导了相位型光栅的衍射光场和光强表达式. 数值模拟结果表明当光栅的占空比为1、相位层引入的相位变化为π时，具有分光功能的±1级将具有最大的衍射效率；不同波长入射时，为保证±1级衍射光强最大且近似相等，选取0级衍射总光强最小的光栅厚度. 实现的相位型光栅可以作为分光器使用.