单轴晶体中非寻常光的折射关系式及其应用
邢 容,朱湘萍,韩 鑫
(湖南科技学院 理学院物理系,湖南 永州 425199)
众所周知,当光入射到双折射晶体时,会出现分别被称作o光(寻常光)和e光(非寻常光)的两种不同的折射光.其中的o光可由折射定律来确定它的传播方向,而e光则一般并不满足折射定律,确定它的传播方向相对较难.
但是在一些应用场合中,掌握e光的传播方向是有用甚至是必须的.例如,2018年,高波等人[1]指出,当KDP/DKDP晶体被用作频率转化元件时,因相位匹配的需要,必须确定e光的传播方向.对于这种情况,若是事先掌握有e光光线的折射关系式,那么只需要代入参数计算就可得出结果了,无需通过实验来获取.
迄今为止,已有多篇文献给出了e光光线的折射关系式[2-6],只是这些关系式有的给出的是e光波矢的折射角[2];有的给出的是e光光线与光轴的夹角[3,6];有的表达式中含有与o光有关的角度[4],较为繁琐;还有的只是给出了e光光线折射角所满足的四次方程[5],难以应用.此外,以上这些关系式还有一个共同的不足,即都没有给出相应的符号规则,这进一步增加了应用上的麻烦.
除了上述文献之外,另有一些文献避开了e光光线普遍性折射关系式的繁琐推导,转而就一些特殊的简单情形进行讨论,也得到了一些有价值的结论.2006年,何波[7,8]推出了e光光线折射角恰为90°时入射角所满足的关系式,借之讨论了入射角超过何值时e光不会出现.2008年,刘丽敏[9]就e光光线恰沿着晶体表面法向这一特殊情形,推出了入射角所满足的关系式,然后讨论了e光会发生负折射现象的条件.2012年,张小宇等人[10]借助惠更斯作图法,推导了e光全反射和负折射现象的临界条件.上述文献实际上都只是得到了临界情形下的折射关系式,虽足以讨论临界点处的情况,但是对偏离临界点后会发生什么就无能为力了.
本文就光轴位于入射面内此一特殊情形,推得了入射光线自各向同性介质入射到单轴晶体时的e光光线折射关系式,以及e光自单轴晶体内出射到各向同性介质时的折射关系式,还给出了相应的符号规则.之后,本文还用得到的折射关系式对几种特殊情况做了讨论.
1 任意单轴晶体中e光的折射关系式及符号规则
设某晶体的光轴与其表面法线夹角为α.现有一束平面波以入射角i自各向同性介质入射于该晶体表面,晶体光轴恰位于其入射面内.取入射在O点处的一条光线考虑,其折射光中e光光线可利用惠更斯作图法得到,结果如图1所示.

图1 惠更斯作图法得到的e光光线
图1中的ie就是e光光线的折射角.可以看到,图中建立有两套坐标系:坐标系x′Oy′ 的纵轴处于界面法向上,并指向各向同性介质一侧;坐标系xOy的纵轴处于光轴方向上,并指向单轴晶体一侧.图中的椭圆曲线代表的是相应时刻下e光的射线面,其方程在xOy中可写作
(1)
式中的no是o光折射率,ne是e光折射率,L则是光从子波源O点发射出来到图中所绘时刻为止所走过的光程.容易知道,A点到O点的距离为
(2)
式中的n是各向同性介质的折射率.图中的射线AB是椭圆曲线的切线,B点是切点.若设B点在xOy中的坐标为(xB,yB),则利用以上条件不难推得
(3)
(4)
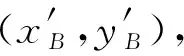
(5)
(6)
将式(3)和式(4)代入式(5)、式(6)中可得
(7)
(8)
在x′Oy′ 下,折射角ie满足
(9)
将式(7)和式(8)代入到式(9)中可得
(10)
此式就是e光光线折射角ie所满足的关系式.此式是在图1所示的入射方向及光轴取向下得到的.对于其他情形,只需按照下面的规则令各角带上相应的符号,那么式(10)依然能够成立(以下的“左”“右”是沿着界面法线自单轴晶体看向各向同性介质时所看到的):
1) 当光轴处于法线的右侧时,α取为正值;否则,α取作负值;
2) 当各向同性介质中光线处于法线的左侧时,i取为正值;否则,i取作负值;
3) 当单轴晶体中e光光线处于法线的右侧时,ie取作正值;否则,ie取作负值.
在此符号规则之下,式(10)中的3个角α、i、ie的取值范围皆为[-π/2,π/2].结合该符号规则,式(10)可适用于任何光轴位于入射面内的情形,无论单轴晶体是正晶体还是负晶体,光线的入射方向如何,以及光轴的取向如何,都可以使用.此外,对式(10)稍作变形之后可得
(11)
利用此式即可计算出当e光自晶体内部出射到各向同性介质时的折射角.式中各角依然满足前述符号规则.
为了验证式(10)的正确性,我们基于惠更斯原理用几何画板绘制了一束光自各向同性介质入射到单轴晶体边界面上时e光光线的光路图.然后利用几何画板自带的度量功能获得了e光光线的折射角,发现与式(10)的计算结果完全一致.
2 e光光线折射角随入射角的变化情况
对于满足折射定律的o光,其折射角会随着入射角的增加而增加,对于e光来说,它的折射角ie随入射角i又是如何变化的呢?
在式(10)中令y=tanie,x=sini,则可有
计算y对x的一阶导数可得
此式表明y′ > 0,因此y会随着x的增加而增加.由此即可知,e光光线的折射角ie会随着入射角i的增加而增加.需要注意的是,这里的ie和i都是在[-π/2,π/2]范围上取值的.由前面给出的符号规则可知,当入射光与e光分处法线两侧时,ie和i要么同取负值要么同取正值.利用上述结论可知,此时与o光相似,若令入射光靠近法线,那么e光必然也同时向法线靠拢.但是,如下文中即将讨论的情形,在一定条件下,入射光可以和e光处于法线的同侧.此时,ie和i的取值必定有相反的符号,若令入射光靠近法线,e光反而会远离法线,这与o光是不同的.若将光线对法线的靠近(或远离)看作为是光线绕法线与界面的交点作相应方向的转动,那么上述e光随入射光变化的两种情况又可以总结为一句话,即当入射光绕入射点转动时,e光必随之作相同方向的转动.这样一来,e光与o光在随入射光变化这一点上是完全相似的,无论e光是否与入射光处于法线的异侧.
3 e光的“负折射”现象
对于满足折射定律的o光,它必定与入射光分列界面法线两侧,而e光却并不会如此,它甚至有时会与入射光处于同侧.
在式(11)中令e光折射角ie= 0可得
(12)
已知ie和i异号时入射光就会与e光处于界面法线同侧,又知道ie会随着i的增加而增加,再结合式(12)即可知,只要sini满足下面的两个条件之一,入射光必与e光处于界面法线同侧
(13)
(14)
需要注意的是,对于给定的晶体,也只有上述两式之一会成立.若某负(正)晶体中成立的是式(13),那么必须有

这就要求该晶体的光轴只能位于法线的右侧(左侧).
4 垂直入射时ie的最大值及其成立条件
利用单轴晶体来产生线偏振光利用的就是晶体中o光与e光在传播方向上的差异.因此,一般而言这种差异越大就越有利于产生较好的线偏振光.
若入射光垂直入射于晶体之上,那么o光就会沿界面法线方向传播,而此时的e光光线却是存在最大折射角的.在式(10)中令入射角i= 0可得
(15)
对此式两边取绝对值可得
容易看出,当
(16)
时,tan|ie|(即|ie|)有最大值.式(16)可化作
(17)
将之代入式(15)可得
(18)
即当光轴的方向满足式(17)时,晶体内e光的偏折程度达到最大,其折射角由式(18)给出.
5 结论
本文就光轴位于入射面内这一特殊情形,推得了单轴晶体中e光的折射关系式,并给出了相应的符号规则.之后,利用该关系式讨论了相关的几个问题.结果发现,e光折射角ie会随着入射角i的增加而增加.这在光路图上表现为,若令入射光在入射面内绕入射点转动,那么与此同时,e光就必定会随之作相同方向的转动.另外还发现,在一定条件下,e光会与入射光出现在界面法线的同侧.此类条件存在两种,任何给定单轴晶体都只能符合其中一种,不存在两种条件都能符合者.最后,本文还推导了垂直入射时e光的最大偏折角及其得以实现的条件.

